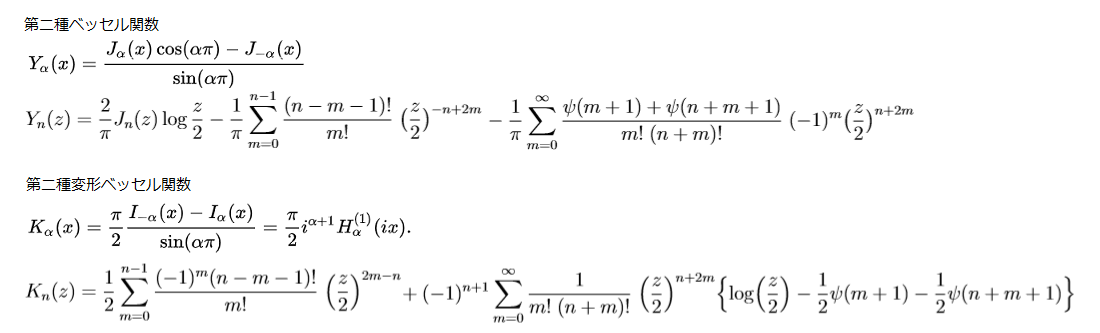
2024/03/25 多倍長演算のルーチンを見直し演算の速度を早くしました。
2024/03/20 多倍長計算のMVG, PVGの配列の長さを修正しました。
2023/10/13
複素数の計算ができるプログラムを追加しました、又、多倍長演算とし、50桁の精度で答えがでる様にしてみました。
2021/09/19 第１種ベッセル関数の計算精度の向上を図ったので、第２種ベッセル関数の検討もしてみました。
次数が実数の場合は、第１種ベッセル関数が使用されるのですが、第２種の整数の場合、第１種と他の計算の差分となり、第２種変形ベッセル関数では全く使用されません。
次数が実数の計算のみ精度の向上が繁栄され、整数の場合は、従来の計算の方が、精度が高くります。
2020/07/01 次数がマイナスの値の時を考慮していませんでしたので修正しました。
第２種ベッセル関数
第１種ベッセル関数を取り上げたので、第２種ベッセル関数についても取り上げました。
ベッセル関数の詳細は、インターネットで参照してください。
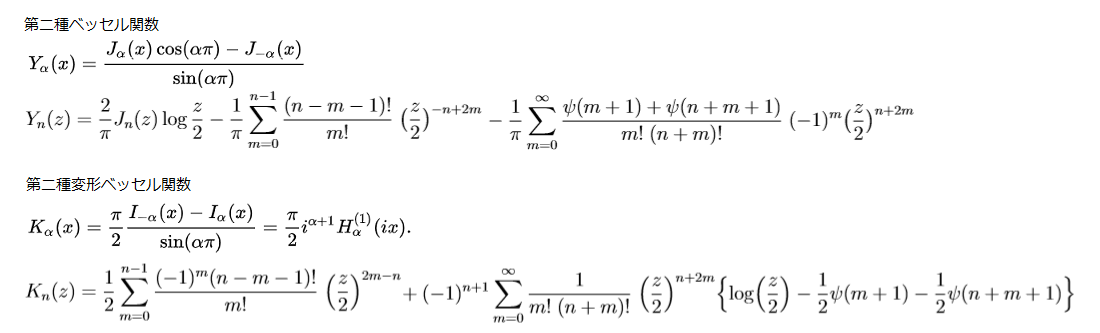
第２種ベッセル関数の計算は、次数が α
実数の場合と、n 整数の場合に分けて計算します。
Yα(x)とKα(x)の計算の場合、α
が整数の場合、分母がゼロに成ってしまう為、整数用のYn(z)、Kn(z)の計算をします。
次数が整数の場合、計算にディガンマ関数が必用となります。
この場合、ディガンマ関数は、整数のみしか使用されないので、整数用のディガンマ関数を使用すればプログラムは簡単になります。
第２種ベッセル関の計算には、第１種ベッセル関数の計算が必要で、次数が実数の場合は、Γ関数が使用されているので、階乗！はΓ関数を使用すれば良いでしょう。
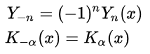次数がマイナスの整数となるときは、左図の関係式となります。
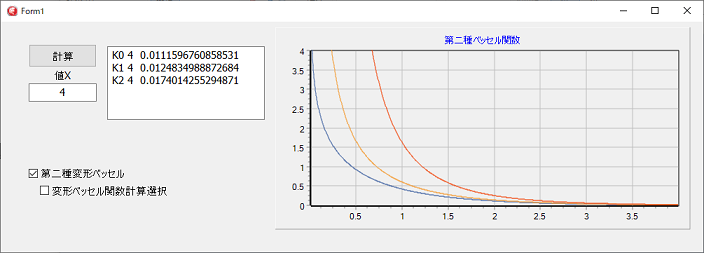
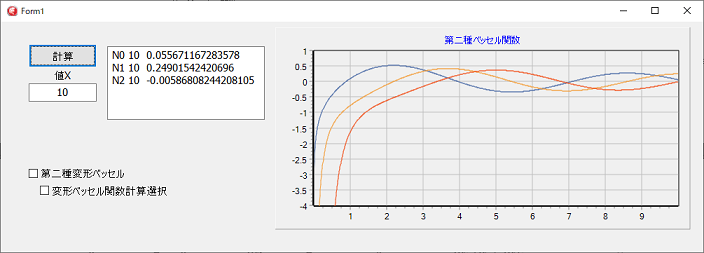左図は、第２種ベッセル関数の次数が整数時のグラフです。
次数が整数なので、第１種ベッセル関数も整数用のルーチンが使用されています。
下側は、第２種変形ベッセル関数です。
変形ベッセル関数には、確認の為、少しルーチンが違う二つのプロぎラムを入れてあります。
∑値の計算で、m=0～∞となっている場所がありますが、Doubleの精度の場合、１７１以上の値の階乗でオーバーフローします。
Doubleの精度であれば、m=0～30程度の計算で問題ないようです。
プログラムでは50迄計算しています。
また、Xの値が大きくなると、演算有効桁数の不足により、誤差が大きくなり正しい結果が得られなくなります。
プログラム
次はプログラムは、次数が正の整数の場合のプログラムです。
// Xの値 積分計算の上限値MNによってオーバーフローを発生するので // コンパイル設定にオーバーフローチックが必須です。 unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.ExtCtrls, Vcl.StdCtrls, Vcl.Buttons, system.Math, system.UITypes, VclTee.TeeGDIPlus, VCLTee.TeEngine, VCLTee.Series, VCLTee.TeeProcs, VCLTee.Chart; type TForm1 = class(TForm) BitBtn1: TBitBtn; Memo1: TMemo; LabeledEdit1: TLabeledEdit; Chart1: TChart; Series1: TLineSeries; CheckBox1: TCheckBox; Series2: TLineSeries; Series3: TLineSeries; CheckBox2: TCheckBox; procedure BitBtn1Click(Sender: TObject); private { Private 宣言 } public { Public 宣言 } function NnX(x: double; n: integer): double; procedure GraphNnX(xmax:double; n: integer); function KnXa(x: double; n: integer): double; function KnXb(x: double; n: integer): double; procedure GraphKnX(xmax:double; n: integer); end; var Form1: TForm1; implementation {$R *.dfm} const gamma = 0.57721566490153286060651209008240243104215; // オイラー定数 // 階乗 m! function factorial(m: integer): double; var i : integer; J : double; begin j := 1; for i := 2 to m do j := j * i; result := j; end; // 第一種ベッセル関数 // X 値 // N 次数 // flag false 通常 true 変形 // Mの値は積分上は∞となっていますが精度上50程度で問題ないようです。 function Bessel(X: double; N: integer; flag: boolean): double; const M = 50; // 値を大きくするとオーバーフローします。 var J, K: Integer; B, S, Jf: double; begin B := 1.0; if N > 1 then begin for K := 1 to N do B := B / K; end; S := B * power((X / 2), N); for J := 1 to M do begin Jf := J; // オバーフロー対策で浮動小数点使用します。 B := B / (Jf * (Jf + N)); if not flag then S := S + power(-1, J) * B * power(X / 2, 2 * J + N) else S := S + B * power(X / 2, 2 * J + N) end; result := S; end; // Ψ(p) ディガンマ関数 function phiN(n: integer): double; var i: integer; s: double; begin if n <= 0 then begin result := 0; exit; end; if n = 1 then begin result := - gamma; exit; end; s := 0; for i := 1 to n - 1 do begin s := s + 1 / i; end; result := s - gamma; end; // 第二種ベッセル関数 // X 値 // n 次数 // Mの値は積分上は∞となっていますが精度上50程度で問題ないようです。 function TForm1.NnX(x: double; n: integer): double; const M = 50; // 値を大きくするとオーバーフローします。 var k : integer; a, b, c: double; begin a := 2 / pi * ln(x / 2) * Bessel(x, n, False); b := 0; for k := 0 to n - 1 do b := b + (factorial(n - k - 1) / factorial(k)) * power(x / 2, 2 * k - n); b := b / pi; c := 0; for k := 0 to M do c := c + power(-1, k) * (phiN(K + 1) + phiN(k + n + 1)) * power(x / 2, 2 * k + n) / (factorial(k) * factorial(n + k)); c := c / pi; result := (a - b - c); end; // 第二種変形ベッセル関数a // X 値 // n 次数 // Mnの値は積分上は∞となっていますが精度上50程度で問題ないようです。 function TForm1.KnXa(x: double; n: integer): double; const MN = 50; // 値を大きくするとオーバーフローします。 var a, b, c: double; p : integer; begin a := power(-1, n + 1) * Bessel(x, n, true) * ln(x / 2); b := 0; for p := 0 to Mn do b := b + 1 / factorial(p) / factorial(n + p) * power(x / 2, 2 * p) * (phiN(p + 1) + phiN(p + n + 1)); b := b * power(- 1, n) / 2 * power(x / 2, n); c := 0; for p := 0 to n - 1 do c := c + power(-1, p) * factorial(n - p - 1) / factorial(p) * power(x / 2, 2 * p); c := c / 2 * power(x / 2, -n); result := a + b + c; end; // 第二種変形ベッセル関数b // X 値 // n 次数 // Mnの値は積分上は∞となっていますが精度上50程度で問題ないようです。 function TForm1.KnXb(x: double; n: integer): double; const Mn = 50; // 値を大きくするとオーバーフローします。 var a, b: double; m : integer; begin a := 0; for m := 0 to n - 1 do a := a + power(-1, m) * factorial(n - m - 1) / factorial(m) * power(x / 2, 2 * m - n); a := a / 2; b := 0; for m := 0 to MN do b := b + 1 / factorial(m) / factorial(n + m) * power(x / 2, 2 * m + n) * (ln(x / 2) - phiN(m + 1) / 2 - phiN(n + m + 1) / 2); b := b * power(-1, n + 1); result := a + b; end; // 第二種ベッセル関数グラフ表示 // xmax Xの最大値 // n 次数 procedure TForm1.GraphNnX(xmax: double; n: integer); const NMAX = 1000; var Y, X: array of double; I : integer; XMIN: double; begin setlength(Y, NMAX); setlength(X, NMAX); setlength(Y, NMAX); XMIN := 0.01; for I := 0 to NMAX - 1 do begin X[I] := XMIN + (xmax - XMIN) * I / NMAX; Y[I] := NnX(x[I], N); end; for I := 0 to NMAX - 1 do begin if n = 0 then Series1.AddXY(X[I], Y[I]); if n = 1 then Series2.AddXY(X[I], Y[I]); if n = 2 then Series3.AddXY(X[I], Y[I]); end; end; // 第二種ベッセル関数グラフ表示 // xmax Xの最大値 // n 次数 procedure TForm1.GraphKnX(xmax: double; n: integer); const NMAX = 1000; var Y, X: array of double; I : integer; XMIN: double; begin setlength(Y, NMAX); setlength(X, NMAX); setlength(Y, NMAX); XMIN := 0.01; for I := 0 to NMAX - 1 do begin X[I] := XMIN + (xmax - XMIN) * I / NMAX; if Checkbox2.Checked = False then Y[I] := KnXa(x[I], N) else Y[I] := KnXb(x[I], N) end; for I := 0 to NMAX - 1 do begin if n = 0 then Series1.AddXY(X[I], Y[I]); if n = 1 then Series2.AddXY(X[I], Y[I]); if n = 2 then Series3.AddXY(X[I], Y[I]); end; end; // 第二種ベッセル関数計算 procedure TForm1.BitBtn1Click(Sender: TObject); var x, Nn: double; ch: integer; begin val(Labelededit1.Text, x, ch); if ch <> 0 then begin MessageDlg('値xに間違いがあります。', mtInformation, [mbOk], 0, mbOk); exit; end; if x <= 0 then begin MessageDlg('値xは0(ゼロ)以上にして下さい。', mtInformation, [mbOk], 0, mbOk); exit; end; if x > 50 then begin MessageDlg('値xが大きすぎます。', mtInformation, [mbOk], 0, mbOk); exit; end; Series1.Clear; Series2.Clear; Series3.Clear; memo1.Clear; if checkbox1.Checked = false then begin if Chart1.LeftAxis.Minimum >= 1 then begin Chart1.LeftAxis.Minimum := -4; Chart1.LeftAxis.Maximum := 1; end else begin Chart1.LeftAxis.Maximum := 1; Chart1.LeftAxis.Minimum := -4; end; GraphNnX(x, 0); Nn := NnX(x, 0); memo1.Lines.Add('N0 ' + floattostr(x) + ' ' + floattostr(Nn)); GraphNnX(x, 1); Nn := NnX(x, 1); memo1.Lines.Add('N1 ' + floattostr(x) + ' ' + floattostr(Nn)); GraphNnX(x, 2); Nn := NnX(x, 2); memo1.Lines.Add('N2 ' + floattostr(x) + ' ' + floattostr(Nn)); end else begin if Chart1.LeftAxis.Minimum >= 4 then begin Chart1.LeftAxis.Minimum := 0; Chart1.LeftAxis.Maximum := 4; end else begin Chart1.LeftAxis.Maximum := 4; Chart1.LeftAxis.Minimum := 0; end; GraphKnX(x, 0); if Checkbox2.Checked = False then Nn := KnXa(x, 0) else Nn := KnXb(x, 0); memo1.Lines.Add('K0 ' + floattostr(x) + ' ' + floattostr(Nn)); GraphKnX(x, 1); if Checkbox2.Checked = False then Nn := KnXa(x, 1) else Nn := KnXb(x, 1); memo1.Lines.Add('K1 ' + floattostr(x) + ' ' + floattostr(Nn)); GraphKnX(x, 2); if Checkbox2.Checked = False then Nn := KnXa(x, 2) else Nn := KnXb(x, 2); memo1.Lines.Add('K2 ' + floattostr(x) + ' ' + floattostr(Nn)); end; end; end.
次は、次数が実数の場合のプログラムです。
計算は非整数と、整数で別の計算となります。
非整数の計算は、簡単ですが、整数の計算は前記の様に複雑な計算となります。
第２種ベッセル関数の計算に第１種ベッセル関数を使用していますが、その計算に、次数が実数のΓ関数をが必要です。
第２種変形ベッセル関数の次数が整数の場合、Γ関数に加えて、ディガンマ関数が必要となります。
階乗！は、全てΓ関数を使用して計算しています。
Ｘの値が大きくなると、有効桁数不足により正しい結果が得られにくなるます。
第１種ベッセル関数の計算精度の向上を図ったので、第２種ベッセル関数の検討もしてみました。
次数が実数の場合は、第１種ベッセル関数が使用されるのですが、第２種の整数の場合、第１種と他の計算の差分となり、第２種変形ベッセル関数では全く使用されません。
次数が実数の計算のみ精度の向上が繁栄され、整数の場合は、従来の計算の方が、精度が高くります。
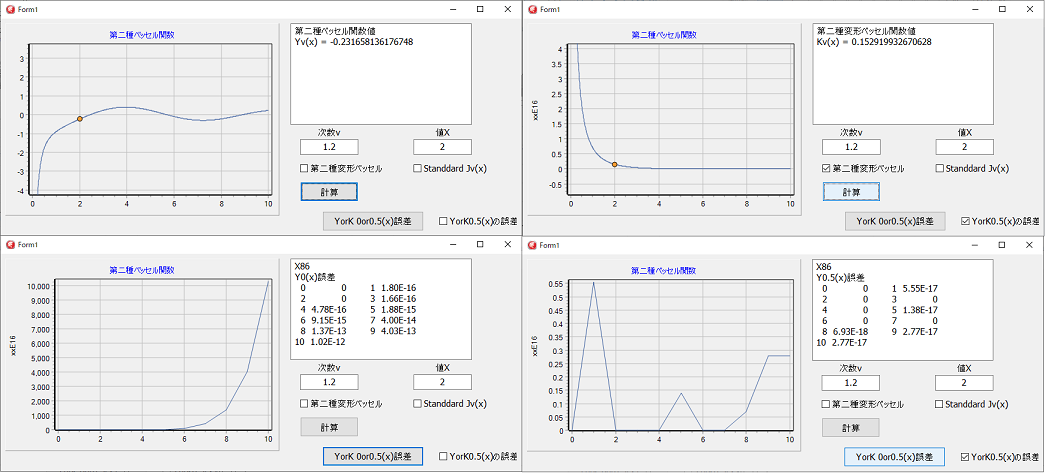
ディガンマ関数は、参考の為に、次数が実数のディガンマ関数を使用しました。
整数のディガンマ関数でよいので、入れ替えれば、プログラムが短くなります。
// Xの値 積分計算の上限値MNによってオーバーフローを発生するので // コンパイル設定にオーバーフローチックが必須です。 // 第二種ベッセル関数の場合次数vが整数の時と、非整数の時で、別の計算をします。 unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.ExtCtrls, Vcl.StdCtrls, Vcl.Buttons, system.Math, system.UITypes, VclTee.TeeGDIPlus, VCLTee.TeEngine, VCLTee.Series, VCLTee.TeeProcs, VCLTee.Chart; type TForm1 = class(TForm) BitBtn1: TBitBtn; Memo1: TMemo; LabeledEdit1: TLabeledEdit; Chart1: TChart; Series1: TLineSeries; CheckBox1: TCheckBox; LabeledEdit2: TLabeledEdit; Series2: TPointSeries; CheckBox2: TCheckBox; Button1: TButton; CheckBox3: TCheckBox; procedure BitBtn1Click(Sender: TObject); procedure Button1Click(Sender: TObject); private { Private 宣言 } public { Public 宣言 } procedure GraphNnX(xmax, v: double); procedure GraphKnX(xmax, v:double); end; var Form1: TForm1; implementation {$R *.dfm} //----------------------------------------------------------------------------- // Gamma_Function(x) function Gamma_Function(z: double): double; const P: array[0..7] of double = ( 676.5203681218851, -1259.1392167224028, 771.32342877765313, -176.61502916214059, 12.507343278686905, -0.13857109526572012, 9.9843695780195716e-6, 1.5056327351493116e-7); max_double_z: double = 171.0; var i : integer; a, t : double; begin if z > max_double_z then begin result := maxdouble; exit; end; if z < 0.5 then begin result := pi / (sin(pi * z) * Gamma_Function(1 - Z)); exit; end; z := z - 1; a := 0.99999999999980993; for i := 0 to length(p) - 1 do a := a + p[i] / (z + i + 1); t := z + length(p) - 0.5; result := sqrt(2 * pi) * power(t, z + 0.5) * exp(-t) * a; end; //***************************************************************************** // 誤差計算用データー const // 第二種変形ベッセル値 // K0.5(x) K05x: array[0..10] of double = (infinity, 0.4610685044478945584396, 0.119937771968061447368, 0.03602598513176459256551, 0.01147762457660805343383, 0.003776613374642882559528, 0.001268286652381588601872, 4.319659804052612483575E-4, 1.486480066651728298787E-4, 5.155708404839055898835E-5, 1.799347809370517960812E-5 ); // K0(x) K0x : array[0..10] of double = (infinity, 0.4210244382407083333356, 0.1138938727495334356527, 0.03473950438627924807235, 0.01115967608585302426975, 0.003691098334042594274735, 0.001243994328013123085233, 4.247957418692318068516E-4, 1.464707052228153870966E-4, 5.088131295645924756974E-5, 1.77800623161676518113E-5 ); // 第二種ベッセル値 // Y0.5(x) Y05x: array[0..10] of double = (maxdouble, -0.4310988680183760795205, 0.234785710406248469174, 0.4560488207946331788468, 0.260766076677178815403, -0.1012177091851083995651, -0.3127610759412769977597, -0.2273558238748285231269, 0.04104480174033306261896, 0.2423255896126850638558, 0.211708866331398152919 ); // Y0(x) Y0x : array[0..10] of double = (maxdouble, 0.08825696421567695798293, 0.5103756726497451195966, 0.3768500100127903819671, -0.01694073932506499190364, -0.3085176252490337800736, -0.2881946839815791540691, -0.02594974396720926488428, 0.2235214893875662205273, 0.2499366982850246760178, 0.05567116728359939142446 ); //----------------------------------------------------------------------------- // DiGamma_Function cutoff: double = 171.0; g: extended = 9.6565781537733158945718737389; a: array[0..8] of extended = ( +1.144005294538510956673085217e+4, -3.239880201523183350535979104e+4, +3.505145235055716665660834611e+4, -1.816413095412607026106469185e+4, +4.632329905366668184091382704e+3, -5.369767777033567805557478696e+2, +2.287544733951810076451548089e+1, -2.179257487388651155600822204e-1, +1.083148362725893688606893534e-4 ); B: array[0..9] of extended = ( 1.0 / (6 * 2), -1.0 / (30 * 4), 1.0 / (42 * 6), -1.0 / (30 * 8), 5.0 / (66 * 10), -691.0 / (2730 * 12), 7.0 / (6 * 14), -3617.0 / (510 * 16), 43867.0 / (796 * 18), -174611.0 / (330 * 20) ); n :integer = sizeof(B) div sizeof(extended); function xDiGamma_Asymptotic_Expansion(x: extended): extended; var m, i: integer; term: array of extended; sum, xx, xj, digamma : extended; begin m := n; // m := 3; // doubleの精度ではm = 3 でOk setlength(term, m); sum := 0; xx := x * x; xj := x; digamma := xj - 1 / (xj + xj); xj := xx; for i := 0 to m - 1 do begin term[i] := B[i] / xj; xj := xj * xx; end; for i := m - 1 downto 0 do sum := sum + term[i]; result := digamma - sum; end; function xDiGamma(x: extended): extended; var lnarg, temp, term, numerator, denominator : extended; n, i: integer; begin lnarg := (g + x - 0.5); numerator := 0; denominator := 0; n := sizeof(a) div sizeof(extended); for i := n - 1 downto 0 do begin temp := x + i; term := a[i] / temp; denominator := denominator + term; numerator := numerator + term / temp; end; denominator := denominator + 1; result := ln(lnarg) - (g / lnarg) - numerator / denominator; end; function xDiGamma_Function(x: extended): extended; var sin_x, cos_x: extended; ix: int64; begin if x > 0 then if x <= cutoff then begin if x >= 1 then result := xDiGamma(x) else result := xDiGamma(x + 1) - (1 / x); exit; end else begin result := xDiGamma_Asymptotic_Expansion(x); exit; end; if x > -MAXExtended then begin ix := trunc(x); if x = ix then begin result := MaxExtended; exit; end; end; sin_x := sin(pi * x); if sin_x = 0 then begin result := MAXExtended; exit; end; cos_x := cos(pi * x); if abs(cos_x) = 1 then begin result := MAXExtended; exit; end; result := xDiGamma(1 - x) - pi * cos_x / sin_x; end; // デイガンマファンクション function DiGamma_Function(x: double): double; var psi: extended; begin psi := xDiGamma_Function(x); if abs(psi) < MAXDouble then begin result := psi; exit; end; if psi < 0 then result := -MaxDouble else result := MaxDouble; end; // 第一種ベッセル関数 Γ関数使用 // X 値 // v 次数 // flag false 通常 true 変形 function BesselG(X: double; v: double; flag: boolean): double; const MN = 100; var M : Integer; B, S : double; begin S := 0; for M := 0 to MN do begin B := 1 / Gamma_Function(M + 1) / Gamma_Function(M + v + 1); // B = 1 / (Γ(m + 1)Γ(m + n + 1)) if not flag then S := S + power(-1, M) * B * power(X / 2, 2 * M + v) else S := S + B * power(X / 2, 2 * M + v) end; result := S; end; //----------------------- new -------------------------------------------------- // X 値 // v 次数 // flag false 通常 true 変形 function Jvx(v, x: double; flag: boolean): extended; var k : integer; g, j, bkk: extended; function Bk(k : integer): extended; var kn : integer; Bn, Y, Zk: extended; begin Y := -(x / 2) * (x / 2); if flag then Y := -Y; Bn := 1; for kn := 1 to k do begin Zk := Y / (kn * (kn + v)); Bn := Zk * Bn; end; result := Bn end; begin g := Gamma_Function(1 + v); bkk := 0; for k := 0 to 100 do bkk := bkk + Bk(k); j := power(x / 2, v) / g * bkk; result := j; end; // 第二種ベッセル関数 // 次数v 非整数 // 値 x function Yax(v, x: double): double; begin if Form1.CheckBox2.Checked = true then result := (BesselG(x, v, false) * cos(v * pi) - BesselG(x, -v, false)) / sin(v * pi) else result := (Jvx(v, x, false) * cos(v * pi) - Jvx(-v, x, false)) / sin(v * pi); end; // 第二種ベッセル関数 // X 値 // n 次数 整数 // Mの値は積分上は∞となっていますが精度上50程度で問題ないようです。 function Ynx(x: double; n: integer): double; const M = 50; // 値を大きくするとオーバーフローします。 var k : integer; a, b, c: double; begin if Form1.CheckBox2.Checked = true then a := 2 / pi * ln(x / 2) * BesselG(x, n, False) else a := 2 / pi * ln(x / 2) * Jvx(n, x, False); b := 0; for k := 0 to n - 1 do b := b + (Gamma_Function(n - k) / Gamma_Function(k + 1)) * power(x / 2, 2 * k - n); b := b / pi; c := 0; for k := 0 to M do c := c + power(-1, k) * (DiGamma_Function(K + 1) + DiGamma_Function(k + n + 1)) * power(x / 2, 2 * k + n) / (Gamma_Function(k + 1) * Gamma_Function(n + k + 1)); c := c / pi; result := (a - b - c); end; // 第二種変形ベッセル関数 // 次数v 非整数 // 値 x function Kax(v, x: double): double; begin if Form1.CheckBox2.Checked = true then result := pi / 2 * ((BesselG(x, -v, true) - BesselG(x, v, true)) / sin(v * pi)) else result := pi / 2 * ((Jvx(-v, x, true) - Jvx(v, x, true)) / sin(v * pi)); end; // 第二種変形ベッセル関数 // X 値 // n 次数 整数 // Mnの値は積分上は∞となっていますが精度上50程度で問題ないようです。 function KnX(x: double; n: integer): double; const MN = 100; // 値を大きくするとオーバーフローします。 var a, b, c: double; p : integer; begin if Form1.CheckBox2.Checked = true then a := power(-1, n + 1) * BesselG(x, n, true) * ln(x / 2) else a := power(-1, n + 1) * Jvx(n, x, true) * ln(x / 2); b := 0; for p := 0 to Mn do b := b + 1 / Gamma_Function(p + 1) / Gamma_Function(n + p + 1) * power(x / 2, 2 * p) * (DiGamma_Function(p + 1) + DiGamma_Function(p + n + 1)); b := b * power(- 1, n) / 2 * power(x / 2, n); c := 0; for p := 0 to n - 1 do c := c + power(-1, p) * Gamma_Function(n - p) / Gamma_Function(p + 1) * power(x / 2, 2 * p); c := c / 2 * power(x / 2, -n); result := a + b + c; end; // 第二種ベッセル関数 // v 次数 // x 値 function Yvx(v, x: double): double; var n: integer; begin n := round(v); if n = v then begin if n < 0 then n := abs(n); result := Ynx(x, n); if v < 0 then result := result * power(-1, n); end else result := Yax(v, x); end; // 第二種ベッセル関数グラフ表示 // xmax Xの最大値 // n 次数 procedure TForm1.GraphNnX(xmax, v: double); const NMAX = 1000; var Y, X: double; I : integer; XMIN: double; begin XMIN := 0.001; for I := 0 to NMAX - 1 do begin X := XMIN + (xmax - XMIN) * I / NMAX; Y := Yvx(v, X); if Y > 20000 then Y := 20000; if Y < -20000 then Y := -20000; Series1.AddXY(X, Y); end; end; // 第二種変形ベッセル関数 // v 次数 // x 値 function kvx(v, x: double): double; var n: integer; begin n := round(v); if n = v then begin if n < 0 then n := abs(n); result := KnX(x, n); end else result := KaX(v, x); end; // 第二種変形ベッセル関数グラフ表示 // xmax Xの最大値 // n 次数 procedure TForm1.GraphKnX(xmax, v: double); const NMAX = 1000; var Y, X: double; I: integer; XMIN: double; begin XMIN := 0.001; for I := 0 to NMAX - 1 do begin X := XMIN + (xmax - XMIN) * I / NMAX; Y := Kvx(v, x); if Y > 20000 then Y := 20000; if Y < -20000 then Y := -20000; Series1.AddXY(X, Y); end; end; // 第二種ベッセル関数計算 procedure TForm1.BitBtn1Click(Sender: TObject); var x, v, y: double; ch: integer; begin val(Labelededit2.Text, v, ch); if ch <> 0 then begin MessageDlg('次数vに間違いがあります。', mtInformation, [mbOk], 0, mbOk); exit; end; val(Labelededit1.Text, x, ch); if ch <> 0 then begin MessageDlg('値xに間違いがあります。', mtInformation, [mbOk], 0, mbOk); exit; end; if x < 0 then begin MessageDlg('値xは0(ゼロ)以上にして下さい。', mtInformation, [mbOk], 0, mbOk); exit; end; if x > 30 then begin MessageDlg('値xが大きすぎます。', mtInformation, [mbOk], 0, mbOk); exit; end; Series1.Clear; Series2.Clear; application.ProcessMessages; chart1.LeftAxis.AutomaticMaximum := False; chart1.LeftAxis.AutomaticMinimum := False; if checkbox1.Checked = false then begin chart1.LeftAxis.Maximum := 4; chart1.LeftAxis.Minimum := -4; end else begin chart1.LeftAxis.Maximum := 10; chart1.LeftAxis.Minimum := -1; end; memo1.Clear; y := 0; if checkbox1.Checked = false then begin if x > 0 then begin y := Yvx(v, x); if Chart1.LeftAxis.Minimum >= y + 4 then begin Chart1.LeftAxis.Minimum := y - 4; Chart1.LeftAxis.Maximum := y + 4; end else begin Chart1.LeftAxis.Maximum := y + 4; Chart1.LeftAxis.Minimum := y - 4; end; GraphNnX(10, v); memo1.Lines.Add('第二種ベッセル関数値'); memo1.Lines.Add('Yv(x) = ' + floatTostr(y)); end; end else begin if x > 0 then begin y := Kvx(v, x); if Chart1.LeftAxis.Minimum >= y + 4 then begin Chart1.LeftAxis.Minimum := y - 1; Chart1.LeftAxis.Maximum := y + 4; end else begin Chart1.LeftAxis.Maximum := y + 4; Chart1.LeftAxis.Minimum := y - 1; end; GraphKnX(10, v); memo1.Lines.Add('第二種変形ベッセル関数値'); memo1.Lines.Add('Kv(x) = ' + floatTostr(y)); end; end; if (x > 0) then Series2.AddXY(x, y); // if (x > 0) and (abs(y) < 9996) then Series2.AddXY(x, y); if x = 0 then begin if checkbox1.Checked = false then begin memo1.Lines.Add('第二種ベッセル関数値'); if v > 0 then memo1.Lines.Add('Yv(x) = - ∞') else memo1.Lines.Add('Yv(x) = ∞'); end else begin memo1.Lines.Add('第二種変形ベッセル関数値'); memo1.Lines.Add('Kv(x) = ∞'); end; end; end; procedure TForm1.Button1Click(Sender: TObject); var i, p, l: integer; yk: extended; def : extended; defs, re, ex, ads, no : string; begin memo1.Clear; Series1.Clear; Series2.Clear; chart1.LeftAxis.AutomaticMaximum := true; chart1.LeftAxis.AutomaticMinimum := False; chart1.LeftAxis.Minimum := 0; {$IFDEF CPUX64} chart1.LeftAxis.Title.Caption := 'xxE16'; Memo1.Lines.Append('X64 double'); {$ELSE} chart1.LeftAxis.Title.Caption := 'xxE16'; Memo1.Lines.Append('X86'); {$ENDIF} if checkbox3.Checked = true then begin if checkbox1.Checked = true then memo1.Lines.Add('K0.5(x)誤差') else memo1.Lines.Add('Y0.5(x)誤差'); end else begin if checkbox1.Checked = true then memo1.Lines.Add('K0(x)誤差') else memo1.Lines.Add('Y0(x)誤差'); end; for i := 0 to 10 do begin if i <> 0 then begin if checkbox3.Checked = true then begin if checkbox1.Checked = true then begin yk := Kvx(1 / 2, i); def := abs(K05x[i] - yk); end else begin yk := Yvx(1 / 2, i); def := abs(Y05x[i] - yk); end; end else begin if checkbox1.Checked = true then begin yk := Kvx(0, i); def := abs(K0x[i] - yk); end else begin yk := Yvx(0, i); def := abs(Y0x[i] - yk); end; end; end else def := 0; {$IFDEF CPUX64} Series1.AddXY(i, def * 1E16); {$ELSE} Series1.AddXY(i, def * 1E16); {$ENDIF} if def <> 0 then defs := floatTostr(def) else defs := ' 0'; l := length(defs); p := pos('E', defs, 1); re := copy(defs, 0, 4); ex := copy(defs, p, l - p + 1); no := inttostr(i); if i < 10 then no := ' ' + no; if i mod 2 = 0 then begin ads := no + ' ' + re + ex; if i = 10 then memo1.Lines.Text := memo1.Lines.Text + ads; end else begin ads := ads + ' ' + no + ' ' + re + ex; memo1.Lines.Append(ads); end; end; end; end.
複素数演算のプログラム
複素数でベッセル関数の計算をする為には、Delphi標準のVariantによる複素数では、有効桁数が不足するので、多倍長演算を使用します。
多倍長の組み込みは MPArithからmparith_2018-11-27.zipをダウンロードして下さい。
Zipファイルを解凍して、解凍したフォルダーにパス(ツール->オプション->Delphiオプション->ライブラリ->ライブラリパス)を追加し、Uses に mp_types, mp_real, mp_cmplx,
mp_baseを追加すれば使用可能になります。
また、今回はMPArithだけではなく、Rudy's Delphi CornerのBigintegerを使用します。
此処には、BigDecimalもあります。
特徴として、四則演算 + - * / 等がそのまま利用できることです。
但し、三角関数や対数関数はありません。
Rudy's Delphi Cornerを開いたら -> Free Coad -> Bigintegers for Delphi 又は BigDecimals for Delph -> 上の行の最後のリンク DelphiBigNumbers project on GitHub ->Coad▼-> Download ZIP でダウンロードします。
DelphiBigNumbers-master.zip がダウンロード出来たら、解凍したSorce フォルダーを、適当な場所にコピーして、そこへパス(ツール->オプション->Delphiオプション->ライブラリ->ライブラリパス)を追加し、usesに Velthuis.BigDecimals Velthuis.BigIntegers を追加すれば、BigDecimal Biginteger が使用可能となります。
使用方法は、解凍されたPDFファイルを参照してください。
Bigintegerは、ベルヌーイ数の計算に使用します、ベルヌーイ数はガンマ関数の計算に必要なのですが、固定値の配列として与えるのが大変なので、プログラム内で作成します。
Bigintegerと、mp_floatはデーター形式が違うので、テキスト形式で値の受け渡しをします。
Bigintegerは整数形式で、mp_floatの方が有効桁数が低い場合、mp_floatは、指数形式で、有効桁数に丸めて読み込むことが出来ます。
此処では、Bigintegerからmp_floatへの変換しか行いません。
* 重要
複素数の計算にべき乗があるのですが、Delphiに用意されている VerComplexPower、
Mp_complex に用意されている、mpc_powは、そのまま使用するには問題があることがわかりました。
説明には、a^b =
exp(b*ln(a))となっているので間違いはないのですが、a と b
が複素数の時、Imaginary部が両方ともゼロ時で aのreal部がマイナスの時は答えのreal部はゼロにならなければなりませんが、意味不明な値が入ります。
もう一つの問題は、乗数 b の値に、**.5 の様に
．５
の値になった時は、整数部の乗数*√の計算なのですがこの時は、realかImaginaryに意味不明な値が値が入ります。
c=a^b
の複素数計算の時、aとb両方の虚数部に0が発生する時は別途正しい答えがでるルーチンを作成する必要があります。
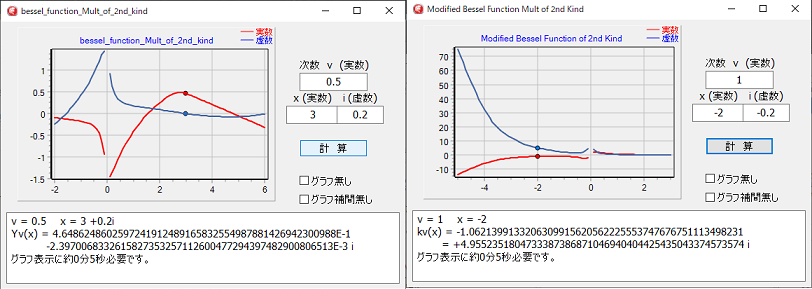入力値v=±100
x=±100の範囲で50桁の精度を目標にしています。
もし、精度を上げる必要がある場合は、mpf_set_default_decprec()
の値を大きくして下さい。
但し、演算速度が遅くまります。
第二種ベッセル関数
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls,
VclTee.TeeGDIPlus, VCLTee.TeEngine, VCLTee.Series, VCLTee.TeeProcs,
VCLTee.Chart, System.Diagnostics, system.UITypes;
type
TForm1 = class(TForm)
Button1: TButton;
Memo1: TMemo;
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
Chart1: TChart;
Series1: TLineSeries;
Series2: TLineSeries;
Series3: TPointSeries;
Series4: TPointSeries;
Series5: TLineSeries;
Series6: TLineSeries;
CheckBox1: TCheckBox;
CheckBox2: TCheckBox;
LabeledEdit3: TLabeledEdit;
procedure Button1Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure FormDestroy(Sender: TObject);
private
{ Private 宣言 }
procedure chart1coment;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
uses system.Math, System.VarCmplx, Velthuis.BigIntegers, mp_real, mp_cmplx, mp_types, mp_base;
{$R *.dfm}
type
DArray = array of double;
var
xt, yt : Darray; // x,y データー akima補間用
m, t : array of mp_float; // m,t akima補間用
BM : array of mp_float; // ベルヌーイ数配列
DG : array of mp_float; // ディガンマ配列
FA : array of mp_float; // 階乗配列
PVG : array of mp_float; // +VΓ
MVG : array of mp_float; // -VΓ
KMV : integer; // Σ計算最大値
gamma : mp_float;
pai, zero, one, two, four : mp_float;
log_2pis2 : mp_float;
const
KMmax = 300; // KM max
Vmax = 100; // v 次数 max
// オイラー定数 有効桁分用意
// 0.577215664901532860606512090082402431042159335939923598805767234884867726777664670936947063291746749514631447249807082480960504
// 01448654283622417399764492353625350033374293733773767394279259525824709491600873520394816567085323315177661152862119950150798479374
gstr0 = '0.577215664901532860606512090082402431042159335939923598805767234884867726777664670936947063291746749514631447249807082480960504';
gstr1 = '0144865428362241739976449235362535003337429373377376739427925952582470949160087352039481656708532331517766115286211995015079847';
gstr = gstr0 + gstr1;
//------------------------------------------------------------------------------
NB = 120; // ベルヌーイ数 配列数 NB + 1
GL = 8; // グラフ基本点数
var
NumeratorString : array[0..NB] of string;
DenominatorString : array[0..NB] of string;
// 最大公約数 ユークリッドの互除法 BigInteger
function gcd_BigInteger(x, y: BigInteger): BigInteger;
var
t : BigInteger;
begin
while y <> 0 do begin
t := x mod y;
x := y;
y := t;
end;
result := x;
end;
// ベルヌーイ数
// Akiyama-Tanigawa algorithm
// BigInteger
procedure Bernoulli_number_BigInteger;
const
n = (NB + 1) * 2;
var
m, j, k : integer;
a : array of BigInteger; // 分子
b : array of BigInteger; // 分母
tmpN : BigInteger; // 分子
tmpD : BigInteger; // 分母
gcd : BigInteger; // 最大公約数
b0 : BigInteger;
begin
setlength(a, n + 1);
setlength(b, n + 1);
k := 0;
for m := 0 to n do begin
a[m] := 1; // 分子 初期値
b[m] := (m + 1); // 分母 初期値
for j := m - 1 downto 0 do begin
tmpN := a[j] * b[j + 1] - a[j + 1] * b[j]; // 分子
tmpN := tmpN * (j + 1); // 〃
tmpD := b[j] * b[j + 1]; // 分母
gcd := gcd_BigInteger(tmpN, tmpD); // 最大公約数
a[j] := tmpN div gcd;
b[j] := tmpD div gcd;
end;
if (m > 0) and (m mod 2 = 0) then begin
b0 := b[0];
b0 := b0 * m * (m -1); // m ベルヌーイ数No
NumeratorString[k] := a[0].tostring;
DenominatorString[k] := b0.tostring;
inc(k);
end;
end;
end;
//------------------------------------------------------------------------------
// ログガンマ多倍長
procedure log_GammaMul(var x, ans : mp_float);
var
v, w: mp_float;
tmp, tmp0, s : mp_float;
i : integer;
begin
mpf_init2(v, w);
mpf_init3(tmp, tmp0, s);
mpf_set1(v); // 1
mpf_set_int(tmp, NB); // tmp=NB
while mpf_is_lt(x, tmp) do begin
mpf_mul(v, x, v); // v = v * x
mpf_add(x, one, x); // x = x + 1
end;
mpf_mul(x, x, tmp); // x^2
mpf_div(one, tmp, w); // w = 1 / x^2
mpf_set0(s); // s = 0
for i := NB downto 1 do begin
mpf_add(s, BM[i], tmp); // tmp = s + B[i]
mpf_mul(tmp, w, s); // s = tmp * w
end;
mpf_add(s, BM[0], tmp); // tmp = s + B[0]
mpf_div(tmp, x, s); // (s + B[0])/x
mpf_add(s, log_2pis2, s); // s = s + ln(2π)/2
mpf_ln(v, tmp); // ln(v)
mpf_sub(s, tmp, s); // s := s - ln(v)
mpf_sub(s, x, s); // s := s - x
mpf_div(one, two, tmp); // tmp = 1/2
mpf_sub(x, tmp, tmp0); // tmp0 = x - 1/2
mpf_ln(x, tmp); // ln(x)
mpf_mul(tmp0, tmp, tmp0); // tmp0 = (x - 1/2) * ln(x)
mpf_add(s, tmp0, ans); // ans = s + (x - 1/2) * ln(x)
mpf_clear2(v, w);
mpf_clear3(tmp, tmp0, s);
end;
// 多倍長ガンマ
// xの値が 0 と負整数の時Γは∞になるのですが処理をしていませんのでエラーになります。
// ケルビンの次数が整数の時は使用されません。
procedure gammaMul(var x, ans: mp_float);
var
tmp, tmp0, logG : mp_float;
begin
mpf_init3(tmp, tmp0, logG);
if mpf_is_lt(x, zero) then begin
mpf_mul(pai, x, tmp); // x*π
mpf_sin(tmp, tmp0); // sin(πx);
mpf_sub(one, x, tmp); // 1-x
log_GammaMul(tmp, logG); // loggamma(1-x);
mpf_exp(logG, logG); // exp(logG)
mpf_div(pai, tmp0, tmp); // π/sin(πx)
mpf_div(tmp, logG, ans); // ans = π/(sin(πx) * logG(1-x))
end
else begin
log_GammaMul(x, logG); // logG
mpf_exp(logG, ans); // exp(logG)
end;
mpf_clear3(tmp, tmp0, logG);
end;
// ディガンマ +整数のみ 多倍長
procedure digammaMUL(n: integer; var ans : mp_float);
var
s, tmp : mp_float;
k : integer;
begin
mpf_init2(s, tmp);
n := n - 1;
mpf_set0(s); // Σ=0
mpf_set0(tmp);
if n >= 0 then begin
for k := 1 to n do begin
mpf_set_int(tmp, k);
mpf_div(one, tmp, tmp); // 1 / k
mpf_add(s, tmp, s);
end;
end;
mpf_sub(s, gamma, ans); // Σ + γ
mpf_clear2(s, tmp);
end;
//------------------------------------------------------------------------------
// 階乗 多倍長
procedure factorialMul(n : integer; var ans: mp_float);
label
EXT;
var
i : integer;
bi: mp_float;
begin
mpf_init(bi);
mpf_set1(ans); // 1
mpf_add(one, one, bi); // bi = 2
if n <= 1 then begin // n <= 1 ans = 1
goto EXT;
end;
for i := 2 to n do begin // n!
mpf_mul(ans, bi, ans); // ans = ans * bi
mpf_add(bi, one, bi); // bi + 1
end;
EXT:
mpf_clear(bi);
end;
//--------------------------- complex power ---------------------------------
procedure mpc_powa(x, y : mp_complex; var ans : mp_complex);
var
ay, ai, zero, harf, two : mp_float;
begin
mpf_init5(ay, ai, zero, harf, two);
mpc_pow(x, y, ans); // exp(y*ln(x))
// xの虚数部とyの虚数部0なら
if mpf_is0(x.im) and mpf_is0(y.im) then begin
mpf_set0(zero); // 0
mpf_set_int(two, 2); // 2
mpf_inv(two, harf); // 1/2 0.5
mpf_abs(y.re, ay); // yの実数部の絶対値
mpf_frac(ay, ai); // yの実数部の絶対値の小数部
mpf_sub(ai, harf, ai); // yの実数部の絶対値の小数部と0.5の差分
// 差分がゼロ(yの実数部の小数部が0.5)
if mpf_is0(ai) then
// xの実数部が0と等しいか0より大きいなら
if mpf_is_ge(x.re, zero) then mpf_set0(ans.im) // 答えの虚数部0
// 0より小さいなら
else mpf_set0(ans.re); // 答えの実数部0
mpf_frac(y.re, ai); // 乗数の小数部
if mpf_is0(ai) then mpf_set0(ans.im); // 整数なら答えの虚数部0
end;
mpf_clear5(ay, ai, zero, harf, two);
end;
//-------------------------------- Jv(x) ---------------------------------------
// jv(x) 多倍長
// xcm= (x+i)値 複素数
// v 次数
// 計算精度の向上には、演算有効桁数のUPとなります。
procedure Jvx(var v : mp_float; var xcm, ri: mp_complex);
var
k : integer;
s, x24k, tmp, tmp0, tmp1 : mp_complex;
xc, xs2 : mp_complex;
kd, nd, vk : mp_float;
khg, kf : mp_float;
tmf, tmf0 : mp_float;
sb : mp_complex;
begin
mpc_init5(s, x24k, tmp, tmp0, tmp1);
mpc_init2(xc, xs2);
mpf_init2(khg, kf);
mpf_init3(kd, nd, vk);
mpf_init2(tmf, tmf0);
mpc_init(sb);
mpc_set0(s); // Σ=0
mpc_set0(sb); // Σback
mpc_set1(x24k);
mpc_div_mpf(xcm, two, xs2); // (x+i)/2
mpc_mul(xs2, xs2, xc); // xc=((x+i)/2)^2)
for k := 0 to KMV do begin
mpf_set1(nd); // 整数数判定値nd初期設定非整数に設定
mpf_set_int(kf, k); // kf = k
mpf_add(v, kf, tmf0); // k + v
mpf_add(tmf0, one, vk); // vk = k + v + 1;
if mpf_is_lt(vk, zero) then begin // vk < 0 時 nxが整数か確認
mpf_int(vk, tmf); // int(vk);
mpf_sub(vk, tmf, nd); // vk - int(vk) vkが負の整数だったら nd = 0
end;
if mpf_is_ne(vk, zero) and mpf_is_ne(nd, zero) then begin // vkが負の整数の時は計算しない
if mpf_is_ge(v, zero) then // vが正数
mpf_copy(PVG[k], tmf) // GammaMul(vk, tmf);
else // vが負数
mpf_copy(MVG[k], tmf); // GammaMul(-vk, tmf);
mpf_mul(FA[k], tmf, khg); // k!Γ(n+k+1) vkが負の整数の時±∞
// mpc_set_mpf(kc, kf, zero); // kc = k + 0i 複素数
// mpc_pow(xc, kc, x24k); // (i(x^2)/4)^k
mpc_div_mpf(x24k, khg, tmp0); // ((i(x^2)/4)^k)/(k!Γ(v+k+1))
if k mod 2 <> 0 then mpc_chs(tmp0, tmp0); // (-1)^k
mpc_add(s, tmp0, s); // Σ
mpc_sub(s, sb, tmp0); // 前のΣ値との差
if mpc_is0(tmp0) then break; // 収束判定
mpc_copy(s, sb);
end;
mpc_mul(x24k, xc, x24k);
end;
mpc_set_mpf(tmp, v, zero); // v + 0i
// x が0で次数vが負数の時power演算ゼロでの除算防止
if mpc_is0(xs2) and mpf_is_lt(v, zero) then // v<0 xs2=0+0i 時は無限大になるので計算しない
else begin
mpc_powa(xs2, tmp, tmp0); // (x/2)^v
mpc_mul(s, tmp0, s); // (x/2)^v * Σ
end;
mpc_copy(s, ri);
mpc_clear5(s, x24k, tmp, tmp0, tmp1);
mpc_clear2(xc, xs2);
mpf_clear2(khg, kf);
mpf_clear3(kd, nd, vk);
mpf_clear2(tmf, tmf0);
mpc_clear(sb);
end;
//--------------------------------- 非整数計算 -------------------------------
// 非整数 多倍長
// 第一種ベッセル関数の差分をsinで除算するため演算精度向上には大きな有効桁数が必要になります。
// 特に次数が負数側に大きく、xの値が小さい時jv(x)の値が非常に小さくなりその差分となるので
// 大きな有効桁数が必要になります。
// xc= (x+i)
procedure ekazMul(var v : mp_float; var xc, ri: mp_complex);
var
sv, sinvp, tmp : mp_float;
harf, av : mp_float;
ipPv, imPv, sipv, tmpc, xc2 : mp_complex;
begin
mpf_init2(harf, av);
mpf_init3(sv, sinvp, tmp);
mpc_init5(ipPv, imPv, sipv, tmpc, xc2);
mpc_copy(xc, xc2);
jvx(v, xc2, ipPv); // J+v
// cos90度がゼロになるように調整
mpf_abs(v, av); // abs(v)
mpf_frac(av, av); // avの小数部
mpf_inv(two, harf); // 0.5
mpf_sub(av, harf, av); // 0.5との差分
if mpf_is0(av) then mpf_set0(tmp) // ±90°だったら0
else begin
mpf_mul(v, pai, tmp); // vπ
mpf_cos(tmp, tmp); // cos(vπ)
end;
mpc_mul_mpf(ipPv, tmp, ipPv); // J+v * cos(vπ)
mpf_chs(v, sv); // -v
jvx(sv, xc2, imPv); // J-v
if not mpc_is0(xc) then begin // xcが0でなかったら
mpc_sub(ipPv, imPv, sipv); // J+v * cos(vπ)- J-v
mpf_mul(v, pai, tmp); // v*π
mpf_sin(tmp, tmp); // sin(v*π)
mpc_div_mpf(sipv, tmp, ri); // (J+v * cos(vπ)- J-v)/sin(v*π)
end;
mpf_clear2(harf, av);
mpf_clear3(sv, sinvp, tmp);
mpc_clear5(ipPv, imPv, sipv, tmpc, xc2);
end;
//---------------------------整数計算-------------------------------------------
// 整数 多倍長計算
// 計算精度の向上には、演算有効桁数のUPとなります。
// z= (x+i)
procedure YnzMul(var v : mp_float; var z, ri : mp_complex);
var
a, b, c, jnz, zc : mp_complex;
z2, ynza, z24, mz24: mp_complex;
tmp, tmp0, tmp1 : mp_complex;
n : mp_float;
mf, nnf, tmf, tmf0 : mp_float;
tmf1, nb : mp_float;
k, m, nn : integer;
ab, cb : mp_complex;
begin
if mpc_is0(z) then begin // z = 0 の時は±∞となるので計算しない
mpc_set0(ri);
exit;
end;
mpc_init5(a, b, c, jnz, zc);
mpc_init4(z2, ynza, z24, mz24);
mpc_init3(tmp, tmp0, tmp1);
mpf_init(n);
mpf_init4(mf, nnf, tmf, tmf0);
mpf_init2(tmf1, nb);
mpc_init2(ab, cb);
mpf_copy(v, nb); // v backup
// 次数を正の整数として計算
mpf_abs(v, n); // n = abs(v)
nn := round(mpf_todouble(n)); // nn = 整数(n)
mpc_div_mpf(z, two, z2); // (x+i)/2 -> z2
mpc_mul(z2, z2, z24); // ((x+i)/2)^2
// jnz
mpc_set0(jnz);
Jvx(n, z, jnz); // Jn(z)
mpf_div(two, pai, tmf0); // 2/π
mpc_ln(z2, tmp); // log(z2)
mpc_mul(tmp, jnz, tmp0); // Jn(z)*log(z2)
mpc_mul_mpf(tmp0, tmf0, jnz); // Jn(z2)log(z2)(2/π)
// jnz end
// a
mpc_set0(a); // Σ=0
mpc_set0(ab); // Σbackup=0
mpc_set1(mz24);
for m := 0 to nn -1 do begin
mpf_div(FA[nn - m - 1], FA[m], tmf); // (n - m - 1)! / m!
mpf_set_int(mf, m);
mpc_set_mpf(tmp0, mf, zero);
// mpc_pow(z24, tmp0, tmp1); // (((x+i)/2)^2)^m
mpc_mul_mpf(tmp1, tmf, tmp0); // (nn - m - 1)! / m! * (((x+i)/2)^2)^m
mpc_add(a, tmp0, a); // Σ
mpc_sub(a, ab, tmp0);
if mpc_is0(tmp0) then break; // 収束判定
mpc_copy(a, ab);
mpc_mul(mz24, z24, mz24);
end;
if mpf_is0(z2.im) then begin
mpf_set_int(nnf, nn); // n
mpf_abs(z2.re, tmf);
mpf_expt(tmf, nnf, tmf0);
if mpf_is_lt(z2.re, zero) then
if nn mod 2 <> 0 then mpf_chs(tmf0, tmf0);
mpc_set_mpf(tmp, tmf0, zero);
mpc_inv(tmp, tmp);
end
else begin
mpf_set_int(nnf, -nn); // -n
mpc_set_mpf(tmp0, nnf, zero); // -n+oi
mpc_pow(z2, tmp0, tmp); // ((((x+i)/2)^2)^m)^(-n+0i)
end;
mpc_mul(a, tmp, tmp1); // Σ* ((((x+i)/2)^2)^m)^(-n+0i)
mpc_div_mpf(tmp1, pai, a); // Σ* ((((x+i)/2)^2)^m)^(-n+0i) / π
// a end
// c
mpc_set0(c);
mpc_set0(cb);
mpc_set1(mz24);
for k:= 0 to KMV do begin
mpf_add(DG[k + 1], DG[nn + k + 1], tmf); // ψ(k+1)+ψ(n+k+1)
mpf_mul(FA[k], FA[nn + k], tmf0); // k!*(n+k)!
// mpf_set_int(kf, k);
// mpc_set_mpf(tmp, kf, zero); // k+0i
// mpc_pow(z24, tmp, tmp); // (((x+i)/2)^2)^k
mpc_mul_mpf(tmp, tmf, tmp); // (ψ(k+1)+ψ(n+k+1)) * (((x+i)/2)^2)^k
mpc_div_mpf(tmp, tmf0,tmp); // ((ψ(k+1)+ψ(n+k+1)) * (((x+i)/2)^2)^k) / (k!*(n+k)!)
if k mod 2 <> 0 then mpc_chs(tmp, tmp); // (-1)^k
mpc_add(c, tmp, c); // Σ
mpc_sub(c, cb, tmp);
if mpc_is0(tmp) then break; // 収束判定
mpc_copy(c, cb);
mpc_mul(mz24, z24, mz24);
end;
mpf_set_int(nnf, nn);
if mpf_is0(z2.im) then begin
mpf_abs(z2.re, tmf);
mpf_expt(tmf, nnf, tmf0);
if mpf_is_lt(z2.re, zero) then
if nn mod 2 <> 0 then mpf_chs(tmf0, tmf0);
mpc_set_mpf(tmp1, tmf0, zero);
// mpc_inv(tmp, tmp);
end
else begin
mpc_set_mpf(tmp0, nnf, zero);
mpc_pow(z2, tmp0, tmp1); // ((x+i)/2)^n
end;
mpc_mul(c, tmp1, tmp); // c * ((x+i)/2)^n
mpc_div_mpf(tmp, pai, c); // (c * ((x+i)/2)) / π
// c end
mpc_sub(jnz, a, tmp); // jnz+a
mpc_sub(tmp, c, ynza); // jnz+a+c
mpf_div(n, two, tmf); // n / 2
mpf_int(tmf, tmf0); // int(n / 2)
mpf_sub(tmf, tmf0, tmf); // n / 2 - int(n / 2)
// nがゼロ以下で奇数だったら 次数が整数でマイナスの時の処理 奇数だとtmf=0.5
if mpf_is_lt(nb, zero) and mpf_is_ne(tmf, zero) then // (-1)^n
mpc_chs(ynza, ri) // 奇数時
else
mpc_copy(ynza, ri); // 偶数時
mpc_clear5(a, b, c, jnz, zc);
mpc_clear4(z2, ynza, z24, mz24);
mpc_clear3(tmp, tmp0, tmp1);
mpf_clear(n);
mpf_clear4(mf, nnf, tmf, tmf0);
mpf_clear2(tmf1, nb);
mpc_clear2(ab, cb);
end;
// akima m,t テーブル作成
// x[] xデーター配列
// y[] yデーター配列
// m[] m係数テーブル
// t[] t係数テーブル
procedure akima_table;
var
ii, n : integer;
a, b, half, tmf, tmf0 : mp_float;
ytm, xtm : array of mp_float;
tmf1 : mp_float;
begin
n := high(xt) + 1;
setlength(ytm, n);
setlength(xtm, n);
for ii := 0 to n - 1 do begin
mpf_init(ytm[ii]);
mpf_init(xtm[ii]);
end;
mpf_init5(a, b, half, tmf, tmf0);
mpf_init(tmf1);
mpf_set_dbl(half, 1 / 2);
for ii := 0 to n -1 do begin
mpf_set_dbl(xtm[ii], xt[ii]);
mpf_set_dbl(ytm[ii], yt[ii]);
end;
// shift data by + 2 in the array and compute the secants
// also calculate extrapolated and end point secants
// 傾斜α両端を除く Δy/Δx
for ii := 0 to n - 2 do begin
mpf_sub(ytm[ii + 1], ytm[ii], tmf);
mpf_sub(xtm[ii + 1], xtm[ii], tmf0);
mpf_div(tmf, tmf0, m[ii + 2]);
end;
// for ii := 0 to n - 2 do
// m[ii + 2] := (yt[ii + 1] - yt[ii]) / (xt[ii + 1] - xt[ii]);
// 端点傾斜処理
mpf_mul(two, m[2], tmf);
mpf_sub(tmf, m[3], m[1]);
// m[1] := 2 * m[2] - m[3];
mpf_mul(two, m[1], tmf);
mpf_sub(tmf, m[2], m[0]);
// m[0] := 2 * m[1] - m[2];
mpf_mul(two, m[n], tmf);
mpf_sub(tmf, m[n - 1], m[n + 1]);
// m[n + 1] := 2 * m[n] - m[n - 1];
mpf_mul(two, m[n + 1], tmf);
mpf_sub(tmf, m[n], m[n + 2]);
// m[n + 2] := 2 * m[n + 1] - m[n];
// 各ポイントの傾斜係数計算
for ii := 0 to n - 1 do begin
mpf_sub(m[ii + 3],m[ii + 2],tmf0);
mpf_abs(tmf0, a);
// a := abs(m[ii + 3] - m[ii + 2]);
mpf_sub(m[ii + 1], m[ii], tmf0);
mpf_abs(tmf0, b);
// b := abs(m[ii + 1] - m[ii]);
mpf_add(a, b, tmf1);
if mpf_is_ne(tmf1, zero) then begin
mpf_mul(a, m[ii + 1], tmf);
mpf_mul(b, m[ii + 2], tmf0);
mpf_add(tmf, tmf0, tmf);
mpf_div(tmf, tmf1, t[ii]);
end
else begin
mpf_add(m[ii + 2], m[ii + 1], tmf);
mpf_mul(half, tmf, t[ii]);
end;
{
if (a + b) <> 0 then begin
t[ii] := (a * m[ii + 1] + b * m[ii + 2]) / (a + b);
end
else
t[ii] := half * (m[ii + 2] + m[ii + 1]);
}
end;
for ii := 0 to n - 1 do begin
mpf_clear(ytm[ii]);
mpf_clear(xtm[ii]);
end;
mpf_clear5(a, b, half, tmf, tmf0);
mpf_clear(tmf1);
end;
// akima 補間値計算
// xx xの値
// x[] xデーター配列
// y[] yデーター配列
// m[] m係数テーブル
// t[] t係数テーブル
// result 補間値y'
function akima_Interpolation(xx: double): double;
var
iB, iM, iT: integer;
a, b, tmf, tmf0 : mp_float;
c, d, e, f, tmf1 : mp_float;
three : mp_float;
begin
mpf_init4(a, b, tmf, tmf0);
mpf_init5(c, d, e, f, tmf1);
mpf_init(three);
mpf_set_int(three, 3);
iB := low(xt); // x[] bottom 配列no
iT := high(xt); // x[] top配列No
// xx値の上下の配列xの配列番号を探す
// XX<x[iB]の場合一番下の区間 XX>x[iT]の場合一番上の区間
while (iT - iB) > 1 do begin
iM := (iB + iT) div 2; // middle配列no
if xt[iM] > xx then
iT := iM
else
iB := iM;
end;
mpf_set_dbl(b, xt[iT] - xt[iB]);
// b := xt[iT] - xt[iB]; // 区間のxの変化量
mpf_set_dbl(a, xx - xt[iB]);
// a := xx - xt[iB]; // x[iB]からのxの値
// 3次akima spline 計算
mpf_set_dbl(c, yt[iB]); // c = yt[ib]
mpf_mul(t[iB], a, d); // d = t[ib] * a
mpf_mul(three, m[iB + 2], tmf); // 3 * m[iB + 2]
mpf_mul(two, t[ib], tmf0); // 2 * t[iB]
mpf_sub(tmf, tmf0, tmf1); // 3 * m[iB + 2] - 2 * t[iB]
mpf_sub(tmf1, t[iB + 1], tmf); // 3 * m[iB + 2] - 2 * t[iB] - t[iB + 1]
mpf_mul(tmf, a, tmf); // (3 * m[iB + 2] - 2 * t[iB] - t[iB + 1]) * a
mpf_mul(tmf, a, tmf); // (3 * m[iB + 2] - 2 * t[iB] - t[iB + 1]) * a * a
mpf_div(tmf, b, e); // (3 * m[iB + 2] - 2 * t[iB] - t[iB + 1]) * a * a / b
mpf_add(t[iB], t[iB + 1], tmf); // t[iB] + t[iB + 1]
mpf_mul(two, m[iB + 2], tmf0); // 2 * m[iB + 2]
mpf_sub(tmf, tmf0, tmf); // t[iB] + t[iB + 1] - 2 * m[iB + 2]
mpf_mul(tmf, a, tmf); // (t[iB] + t[iB + 1] - 2 * m[iB + 2]) * a
mpf_mul(tmf, a, tmf); // (t[iB] + t[iB + 1] - 2 * m[iB + 2]) * a * a
mpf_mul(tmf, a, tmf); // (t[iB] + t[iB + 1] - 2 * m[iB + 2]) * a * a * a
mpf_mul(b, b, tmf0); // b * b
mpf_div(tmf, tmf0, f); // (t[iB] + t[iB + 1] - 2 * m[iB + 2]) * a * a * a / (b * b)
mpf_add(c, d, tmf); // c + d
mpf_add(tmf, e, tmf); // c + d + e
mpf_add(tmf, f, tmf); // c + d + e + f
result := mpf_todouble(tmf);
{
result := yt[iB]
+ t[iB] * a
+ (3 * m[iB + 2] - 2 * t[iB] - t[iB + 1]) * a * a / b
+ (t[iB] + t[iB + 1] - 2 * m[iB + 2]) * a * a * a / (b * b);
}
mpf_clear4(a, b, tmf, tmf0);
mpf_clear5(c, d, e, f, tmf1);
mpf_clear(three);
end;
procedure TForm1.chart1coment;
begin
Chart1.Canvas.Font.Size := 8;
Chart1.Canvas.Font.Style := [];
chart1.Canvas.Font.Color := clred;
chart1.Canvas.TextOut(chart1.Width - 30, 1,'実数');
chart1.Canvas.Font.Color := clblue;
chart1.Canvas.TextOut(chart1.Width - 30, 13,'虚数');
chart1.Canvas.Pen.Width := 1;
chart1.Canvas.Pen.Color := clred;
chart1.Canvas.MoveTo(chart1.Width - 50, 6);
chart1.Canvas.LineTo(chart1.Width - 32, 6);
chart1.Canvas.Pen.Color := clblue;
chart1.Canvas.MoveTo(chart1.Width - 50, 18);
chart1.Canvas.LineTo(chart1.Width - 32, 18);
end;
//------------------------------------------------------------------------------
// ta[] グラフ用計算点配列
procedure TForm1.Button1Click(Sender: TObject);
label
EXT;
const
// ta : array[0..GL - 1] of double = (0.5, 1, 1.5, 2, 2.5, 3, 3.5, 4);
ta : array[0..GL - 1] of double = (0.08, 0.16, 0.32, 0.64, 1.2, 2, 3, 4);
YPM = 1E304; // double の最大値制限 オーバーフロー対策
YMM = - YPM;
var
ch, i, xi: integer;
kerx, keix: double;
kerxe, keixe: double;
x, v, xv, ia : double;
xmin, xmax, dx, dxf: double;
ymin, ymax: double;
xm, vm, ndm, dxm: mp_float;
avm, andm: mp_float;
tmp, nd : mp_float;
xc, epc, ri, tmc : mp_complex;
berl : Darray;
beil : Darray;
beru : Darray;
beiu : Darray;
xl : Darray;
xu : Darray;
vmaxmes : string;
GCF : integer;
StopWatch : TStopwatch;
ElapsedMillseconds : Int64;
mm, ss, ms : integer;
k : integer;
vk, tmf, tmf0, iam : mp_float;
GU, GS : integer;
// xの値を複素数に変換
procedure xtoxc(var x, ia : mp_float; var xc : mp_complex);
begin
mpc_set_mpf(xc, x, ia); // xc
end;
// doubleの最大値の制限
function maxmin(x : double): double;
begin
result := x;
if x > YPM then result := YPM;
if x < YMM then result := YMM;
end;
begin
memo1.Clear;
val(labelededit1.Text, v, ch);
if ch <> 0 then begin
application.MessageBox('次数vの値に間違いがあります。','注意', 0);
exit;
end;
if v > vmax then begin
vmaxmes := 'Vの値は ' + intTostr(vmax) + '以下にして下さい。';
application.MessageBox(pwideChar(vmaxmes),'注意', 0);
exit;
end;
{ if V < -31 then begin // マイナス側を広げるには得演算の有効桁数を増やす必要があります。
vmaxmes := 'Vの値は -31 より大きしてください。';
application.MessageBox(pwideChar(vmaxmes),'注意', 0);
exit;
end; }
val(labelededit2.Text, x, ch);
if ch <> 0 then begin
application.MessageBox('xの値に間違いがあります。','注意', 0);
exit;
end;
if abs(x) > 100 then begin
vmaxmes := 'xの値は±100迄にしてください';
application.MessageBox(pchar(vmaxmes),'注意', 0);
exit;
end;
if (v < 0) and (x <> 0) then
if abs(x) < 1E-10 then begin
vmaxmes := 'vが負数の時はxの絶対値は1E-10より大きしてください。';
application.MessageBox(pwideChar(vmaxmes),'注意', 0);
exit;
end;
val(labelededit3.Text, ia, ch);
if ch <> 0 then begin
application.MessageBox('i の値に間違いがあります。','注意', 0);
exit;
end;
if abs(ia) > 100 then begin
vmaxmes := 'i の値は±100迄にしてください';
application.MessageBox(pchar(vmaxmes),'注意', 0);
exit;
end;
// KMV := 50 + round((abs(x) + abs(ia)) * 10);
// if KMV > KMmax then KMV := KMmax; // Σ 0～kMAX
kmv := KMmax;
mpf_init4(vm, xm, ndm, dxm);
mpf_init2(avm, andm);
mpf_init2(tmp, nd);
mpf_init4(vk, tmf, tmf0, iam);
mpc_init4(xc, epc, ri, tmc);
mpf_read_decimal(vm, PAnsiChar(ansistring(labelededit1.Text + #00)));
mpf_read_decimal(xm, PAnsiChar(ansistring(labelededit2.Text + #00)));
mpf_read_decimal(iam, PAnsiChar(ansistring(labelededit3.Text + #00)));
memo1.Clear;
mpf_int(vm, ndm);
mpf_sub(vm, ndm, ndm); // 整数ならndm = 0
mpf_abs(ndm, andm); // 小数部の値
mpf_read_decimal(dxm, PAnsiChar(ansistring('1E-10' + #00)));
if mpf_is_lt(andm, dxm) and mpf_is_ne(ndm, zero) then begin
application.MessageBox('次数vの値の小数部は 1E-10 より大きくしてください。','注意', 0);
goto EXT;
end;
// Γ値配列計算
mpf_abs(vm, avm); // +v
for k := 0 to KMmax do begin
mpf_set_int(tmf, k); // k
mpf_add(tmf, avm, tmf0); // v + k
mpf_add(tmf0, one, vk); // vk= v + k + 1
gammaMul(vk, PVG[k]); // Γ(n+k+1)
end;
mpf_chs(avm, avm); // -v
for k := 0 to KMmax do begin
mpf_set1(nd);
mpf_set_int(tmf, k); // k
mpf_add(tmf, avm, tmf0); // -v + k
mpf_add(tmf0, one, vk); // vk= -v + k + 1
if mpf_is_lt(vk, zero) then begin // vk < 0 時 nxが整数か確認
mpf_int(vk, tmf); // int(vk);
mpf_sub(vk, tmf, nd); // vk - int(vk) vkが負の整数だったら nd = 0
end;
if mpf_is_ne(vk, zero) and mpf_is_ne(nd, zero) then // vkが負の整数でない
gammaMul(vk, MVG[k]) // Γ(n+k+1)
else // vkが負の整数
mpf_set0(MVG[k]); // Γ(n+k+1) = 0
end;
if ia >= 0 then vmaxmes := ' +' + floatTostr(ia) + 'i'
else vmaxmes := ' ' + floatTostr(ia) + 'i';
memo1.Lines.Append('v = ' + floatTostr(v) + ' x = ' + floatTostr(x) + vmaxmes);
StopWatch := TStopwatch.StartNew;
// 表示値の計算
mpf_abs(vm, avm);
xToxc(xm, iam, xc);
// xc <> 0 の時の表示設定
if not mpc_is0(xc) then begin // xc <> 0
if mpf_is_ne(ndm, zero) then
ekazMul(vm, xc, ri)
else
ynzMul(vm, xc, ri);
memo1.Lines.Append('Yv(x) = ' + string(mpf_decimal(ri.re, 50)));
// i部表示
if mpf_is_ge(ri.im, zero) then // im>=0 表示iに+符号追加
memo1.Lines.Append(' +' + string(mpf_decimal(ri.im, 50)) + ' i')
else // im<0 表示i
memo1.Lines.Append(' ' + string(mpf_decimal(ri.im, 50)) + ' i');
kerxe := mpf_todouble(ri.re);
keixe := mpf_todouble(ri.im);
end
// xc = 0 の時の表示値設定
else begin // xc = 0
// v >= 0
if mpf_is_ge(vm, zero) then begin
memo1.Lines.Append('Yv(x) = -INF'); // 実数部 -∞
memo1.Lines.Append(' = +0i'); // 虚数部 0i
kerxe := -infinity;
keixe := 0;
end
// v < 0
else begin
mpf_int(avm, tmp); // avmの整数部
mpf_sub(avm, tmp, tmf0); // avmの小数部
mpf_div(one, two, tmf); // 0.5
// avmの小数部が0.5
if mpf_is_eq(tmf, tmf0) then begin
memo1.Lines.Append('Yv(x) = 0'); // 実数部 0
memo1.Lines.Append(' = +0i'); // 虚数部 0i
kerxe := 0;
keixe := 0;
end
// avmの小数部が0.5でなかったら0.5加算します
else begin
mpf_add(avm, tmf, tmp); // avm + 0.5
mpf_int(tmp, tmf0); // avm + 0.5 -> 整数
mpf_div(tmf0, two, tmf0); // 整数/2
mpf_frac(tmf0, tmf0); // 小数部取り出し
// avm+0.5が偶数だったら
if mpf_is0(tmf0) then begin
memo1.Lines.Append('Yv(x) = -INF'); // 実数部 -∞
kerxe := -infinity;
end
// amv+0.5が奇数だったら
else begin
memo1.Lines.Append('Yv(x) = INF'); // 実数部 +∞
kerxe := infinity;
end;
memo1.Lines.Append(' = +0i'); // 虚数部 0i
keixe := 0;
end;
end;
end;
StopWatch.Stop;
ElapsedMillseconds := StopWatch.ElapsedMilliseconds;
// goto EXT;
ms := ElapsedMillseconds * (GL + 1) * 2 + 2000;
mm := ms div 60000;
ss := (ms mod 60000) div 1000;
vmaxmes := 'グラフ表示に約' + inttostr(mm) + '分' + inttostr(ss) + '秒必要です。';
memo1.Lines.Append(vmaxmes);
series1.Clear;
series2.Clear;
series3.Clear;
series4.Clear;
series5.Clear;
series6.Clear;
application.ProcessMessages;
if (checkbox2.Checked = true) then begin // グラフ無だったら終了
Chart1.Canvas.Font.Style := [fsBold];
Chart1.Canvas.Font.size := 8;
Chart1.Canvas.TextOut(170, 115,'グラフ無し');
goto EXT;
end;
if ElapsedMillseconds > 500 then begin
vmaxmes := vmaxmes + #13#10 + 'グラフの表示をしますか?';
if MessageDlg(vmaxmes , mtConfirmation, [mbYes, mbNo], 0, mbYes) = mrNo then begin
Chart1.Canvas.Font.Style := [fsBold];
Chart1.Canvas.Font.size := 8;
Chart1.Canvas.TextOut(170, 115,'グラフ無し');
goto EXT;
end;
end;
// 最大値最小値の検索とグラフデーター作成
xi := round(x);
xmin := xi - 4;
GCF := 0;
if (x >= -2) and (x <= 2) then GCF := 1;
if (x >= -3) and (x <= -2) then GCF := 2;
if (x >= 2) and (x <= 3) then GCF := 3;
if (x >= -4) and (x <= -3) then GCF := 4;
if (x >= 3) and (x <= 4) then Gcf := 5;
case GCF of
0: xmin := xi - 4;
1: xmin := -4;
2: xmin := -5;
3: xmin := -3;
4: xmin := -6;
5: xmin := -2;
end;
xmax := xmin + 8;
case GCF of
0 : begin
setlength(berl, GL + GL);
setlength(beil, GL + GL);
setlength(xt, GL + GL); setlength(yt, GL + GL);
setlength(xl, GL + GL);
end;
1, 2, 3, 4, 5:
begin
setlength(berl, GL); setlength(beru, GL);
setlength(beil, GL); setlength(beiu, GL);
setlength(xt, GL); setlength(yt, GL);
setlength(xl, GL); setlength(xu, GL);
end;
end;
dxf := 0.1;
dx := dxf;
GS := 40;
GU := 40;
ch := GCF;
case GCF of
0 :
begin
dx := (xmax - xmin) / (Gl + GL - 1);
for i := 0 to GL + GL - 1 do xl[i] := dx * i + xmin;
xl[0] := xl[0] + dxf;
xl[GL + GL - 1] := xl[GL + GL - 1] - dxf;
GS := 80;
end;
1 :
begin
for i := 0 to GL - 1 do begin
xu[i] := ta[i];
xl[GL - i - 1] := -ta[i];
end;
end;
else // 2,3,4,5
begin
for i := 0 to GL - 1 do begin
xu[i] := ta[i];
xl[GL - i - 1] := -ta[i];
end;
case ch of
2 : begin dx := 5 / 4; dxf := 3 / 4; GS := 50; GU := 30; end;
3 : begin dx := 3 / 4; dxf := 5 / 4; GS := 30; GU := 50; end;
4 : begin dx := 6 / 4; dxf := 2 / 4; GS := 60; GU := 20; end;
5 : begin dx := 2 / 4; dxf := 6 / 4; GS := 20; GU := 60; end;
end;
for i := 0 to Gl - 1 do begin
xl[i] := xl[i] * dx;
xu[i] := xu[i] * dxf;
end;
end;
end;
// グラフ用データー作成
ymin := 0;
ymax := 0;
case GCF of
0 : begin
for i := 0 to GL + GL - 1 do begin
xv := xl[i];
mpf_set_dbl(tmp, xv);
xToxc(tmp, iam, xc);
if mpf_is_ne(ndm, zero) then
ekazMul(vm, xc, ri)
else
ynzMul(vm, xc, ri);
berl[i] := maxmin(mpf_todouble(ri.re));
beil[i] := maxmin(mpf_todouble(ri.im));
if berl[i] > ymax then ymax := berl[i];
if beil[i] > ymax then ymax := beil[i];
if berl[i] < ymin then ymin := berl[i];
if beil[i] < ymin then ymin := beil[i];
end;
end;
1, 2, 3, 4, 5:
for i := 0 to GL - 1 do begin
xv := xl[i];
mpf_set_dbl(tmp, xv);
xToxc(tmp, iam, xc);
if mpf_is_ne(ndm, zero) then
ekazMul(vm, xc, ri)
else
ynzMul(vm, xc, ri);
berl[i] := maxmin(mpf_todouble(ri.re));
beil[i] := maxmin(mpf_todouble(ri.im));
if berl[i] > ymax then ymax := berl[i];
if beil[i] > ymax then ymax := beil[i];
if berl[i] < ymin then ymin := berl[i];
if beil[i] < ymin then ymin := beil[i];
xv := xu[i];
mpf_set_dbl(tmp, xv);
xToxc(tmp, iam, xc);
if mpf_is_ne(ndm, zero) then
ekazMul(vm, xc, ri)
else
ynzMul(vm, xc, ri);
beru[i] := maxmin(mpf_todouble(ri.re));
beiu[i] := maxmin(mpf_todouble(ri.im));
if beru[i] > ymax then ymax := beru[i];
if beiu[i] > ymax then ymax := beiu[i];
if beru[i] < ymin then ymin := beru[i];
if beiu[i] < ymin then ymin := beiu[i];
end;
end;
if abs(ymin) < 0.1 then ymin := -0.1;
if ymax < 0.1 then ymax := 0.1;
if kerxe > ymax then kerxe := ymax;
if kerxe < ymin then kerxe := ymin;
if keixe > ymax then keixe := ymax;
if keixe < ymin then keixe := ymin;
series3.AddXY(x, kerxe);
series4.AddXY(x, keixe);
if checkbox1.Checked = true then
case GCF of
0:
begin
for i := 0 to GL + GL - 1 do begin
series1.AddXY(xl[i], berl[i]);
series2.AddXY(xl[i], beil[i]);
end;
end;
1, 2, 3, 4, 5 :
begin
for i := 0 to GL - 1 do begin
series1.AddXY(xl[i], berl[i]);
series2.AddXY(xl[i], beil[i]);
series5.AddXY(xu[i], beru[i]);
series6.AddXY(xu[i], beiu[i]);
end;
end;
end;
if checkbox1.Checked = false then
// グラフ表示
case GCF of
0:
begin
for i := 0 to GL + GL - 1 do begin
xt[i] := xl[i];
yt[i] := berl[i];
end;
akima_table;
dx := (xt[GL + GL - 1] - xt[0]) / GS;
for i := 0 to GS do begin
xv := dx * i + xt[0];
kerx := maxmin(akima_Interpolation(xv));
series1.AddXY(xv, kerx);
end;
for i := 0 to GL + GL - 1 do yt[i] := beil[i];
akima_table;
for i := 0 to GS do begin
xv := dx * i + xt[0];
keix := maxmin(akima_Interpolation(xv));
series2.AddXY(xv, keix);
end;
end;
1, 2, 3, 4, 5 :
begin
for i := 0 to GL- 1 do begin
xt[i] := xl[i];
yt[i] := berl[i];
end;
akima_table;
dx := xt[0] / GS;
for i := GS downto 1 do begin
xv := dx * i;
kerx := maxmin(akima_Interpolation(xv));
series1.AddXY(xv, kerx);
end;
for i := 0 to GL- 1 do yt[i] := beil[i];
akima_table;
for i := GS downto 1 do begin
xv := dx * i;
keix := maxmin(akima_Interpolation(xv));
series2.AddXY(xv, keix);
end;
if mpf_is0(xm) then begin
// series1.AddXY(0, kerxe);
// series2.AddXY(0, keixe);
series5.AddXY(0, kerxe);
series6.AddXY(0, keixe);
end;
for i := 0 to GL- 1 do begin
xt[i] := xu[i];
yt[i] := beru[i];
end;
akima_table;
dx := xt[GL - 1] / GU;
for i := 1 to GU do begin
xv := dx * i;
kerx := maxmin(akima_Interpolation(xv));
series5.AddXY(xv, kerx);
end;
for i := 0 to GL- 1 do yt[i] := beiu[i];
akima_table;
for i := 1 to GU do begin
xv := dx * i;
keix := maxmin(akima_Interpolation(xv));
series6.AddXY(xv, keix);
end;
end;
end;
application.ProcessMessages;
chart1coment;
EXT:
mpf_clear4(vm, xm, ndm, dxm);
mpf_clear2(avm, andm);
mpf_clear2(tmp, nd);
mpf_clear4(vk, tmf, tmf0, iam);
mpc_clear4(xc, epc, ri, tmc);
end;
procedure TForm1.FormCreate(Sender: TObject);
var
i : integer;
N, D, tmp : mp_float;
begin
mpf_set_default_decprec(200); // 有効桁数200 50桁の精度に必要です。
// 演算時間が非常に長くなります。
setlength(BM, NB + 1); // ベルヌーイ数 配列
setlength(DG, KMmax + Vmax + 2); // ディガンマ
setlength(FA, KMmax + Vmax + 1); // 階乗
setlength(t, GL + GL); // akima 補間値計算 配列 t
setlength(m, GL + GL + 3); // akima 補間値計算 配列 m
setlength(PVG, KMmax + 1); // +vΓ
setlength(MVG, KMmax + 1); // -vΓ
for i := 0 to NB do mpf_init(BM[i]);
for i := 0 to KMmax + Vmax + 1 do mpf_init(DG[i]);
for i := 0 to KMmax + Vmax do mpf_init(FA[i]);
for i := 0 to KMmax do mpf_init(PVG[i]);
for i := 0 to KMmax do mpf_init(MVG[i]);
mpf_init3(N, D, tmp);
mpf_init(gamma);
mpf_init5(pai, zero, one, two, four);
mpf_init(log_2pis2);
mpf_set_pi(pai); // π
mpf_set0(zero); // 0
mpf_set1(one); // 1
mpf_set_int(two, 2); // 2
mpf_set_int(four, 4); // 4
mpf_mul(pai, two, tmp); // 2π
mpf_ln(tmp, tmp); // ln(2π)
mpf_div(tmp, two, log_2pis2); // ln(2π)/2
mpf_read_decimal(gamma, PAnsiChar(ansistring(gstr + #00))); // γ
for i := 0 to GL + GL - 1 do mpf_init(t[i]);
for i := 0 to GL + GL + 2 do mpf_init(m[i]);
Bernoulli_number_BigInteger; // ベルヌーイ数作成
for i := 0 to NB do begin
mpf_read_decimal(N, PAnsiChar(ansistring(NumeratorString[i] + #00)));
mpf_read_decimal(D, PAnsiChar(ansistring(DenominatorString[i] + #00)));
mpf_div(N, D, BM[i]);
end;
for i := 0 to KMmax + Vmax + 1 do begin
digammaMUL(i, D);
mpf_copy(D, DG[i]);
end;
for i := 0 to KMmax + Vmax do begin
factorialMul(i, N);
mpf_copy(N, FA[i]);
end;
memo1.Clear;
mpf_clear3(N, D, tmp);
end;
procedure TForm1.FormDestroy(Sender: TObject);
var
i : integer;
begin
for i := 0 to NB do mpf_clear(BM[i]);
for i := 0 to KMmax + Vmax + 1 do mpf_clear(DG[i]);
for i := 0 to KMmax + Vmax do mpf_clear(FA[i]);
for i := 0 to GL + GL - 1 do mpf_clear(t[i]);
for i := 0 to GL + GL + 2 do mpf_clear(m[i]);
for i := 0 to KMmax do mpf_clear(PVG[i]);
for i := 0 to KMmax do mpf_clear(MVG[i]);
mpf_clear(gamma);
mpf_clear5(pai, zero, one, two, four);
mpf_clear(log_2pis2);
end;
end.
第二種変形ベッセル関数
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls,
VclTee.TeeGDIPlus, VCLTee.TeEngine, VCLTee.Series, VCLTee.TeeProcs,
VCLTee.Chart, System.Diagnostics, system.UITypes;
type
TForm1 = class(TForm)
Button1: TButton;
Memo1: TMemo;
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
Chart1: TChart;
Series1: TLineSeries;
Series2: TLineSeries;
Series3: TPointSeries;
Series4: TPointSeries;
Series5: TLineSeries;
Series6: TLineSeries;
CheckBox1: TCheckBox;
CheckBox2: TCheckBox;
LabeledEdit3: TLabeledEdit;
procedure Button1Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure FormDestroy(Sender: TObject);
private
{ Private 宣言 }
procedure chart1coment;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
uses system.Math, System.VarCmplx, Velthuis.BigIntegers, mp_real, mp_cmplx, mp_types, mp_base;
{$R *.dfm}
type
DArray = array of double;
var
xt, yt : Darray; // x,y データー akima補間用
m, t : array of mp_float; // m,t akima補間用
BM : array of mp_float; // ベルヌーイ数配列
DG : array of mp_float; // ディガンマ配列
FA : array of mp_float; // 階乗配列
PVG : array of mp_float; // +VΓ
MVG : array of mp_float; // +VΓ
KMV : integer; // Σ計算最大値
gamma : mp_float;
pai, zero, one, two, four : mp_float;
log_2pis2 : mp_float;
const
KMmax = 250; // KM max
Vmax = 100; // v 次数 max
// オイラー定数 有効桁分用意
// 0.577215664901532860606512090082402431042159335939923598805767234884867726777664670936947063291746749514631447249807082480960504
// 01448654283622417399764492353625350033374293733773767394279259525824709491600873520394816567085323315177661152862119950150798479374
gstr0 = '0.577215664901532860606512090082402431042159335939923598805767234884867726777664670936947063291746749514631447249807082480960504';
gstr1 = '0144865428362241739976449235362535003337429373377376739427925952582470949160087352039481656708532331517766115286211995015079847';
gstr = gstr0 + gstr1;
//------------------------------------------------------------------------------
NB = 120; // ベルヌーイ数 配列数 NB + 1
GL = 8; // グラフ基本点数
var
NumeratorString : array[0..NB] of string;
DenominatorString : array[0..NB] of string;
// 最大公約数 ユークリッドの互除法 BigInteger
function gcd_BigInteger(x, y: BigInteger): BigInteger;
var
t : BigInteger;
begin
while y <> 0 do begin
t := x mod y;
x := y;
y := t;
end;
result := x;
end;
// ベルヌーイ数
// Akiyama-Tanigawa algorithm
// BigInteger
procedure Bernoulli_number_BigInteger;
const
n = (NB + 1) * 2;
var
m, j, k : integer;
a : array of BigInteger; // 分子
b : array of BigInteger; // 分母
tmpN : BigInteger; // 分子
tmpD : BigInteger; // 分母
gcd : BigInteger; // 最大公約数
b0 : BigInteger;
begin
setlength(a, n + 1);
setlength(b, n + 1);
k := 0;
for m := 0 to n do begin
a[m] := 1; // 分子 初期値
b[m] := (m + 1); // 分母 初期値
for j := m - 1 downto 0 do begin
tmpN := a[j] * b[j + 1] - a[j + 1] * b[j]; // 分子
tmpN := tmpN * (j + 1); // 〃
tmpD := b[j] * b[j + 1]; // 分母
gcd := gcd_BigInteger(tmpN, tmpD); // 最大公約数
a[j] := tmpN div gcd;
b[j] := tmpD div gcd;
end;
if (m > 0) and (m mod 2 = 0) then begin
b0 := b[0];
b0 := b0 * m * (m -1); // m ベルヌーイ数No
NumeratorString[k] := a[0].tostring;
DenominatorString[k] := b0.tostring;
inc(k);
end;
end;
end;
//------------------------------------------------------------------------------
// ログガンマ多倍長
procedure log_GammaMul(var x, ans : mp_float);
var
v, w: mp_float;
tmp, tmp0, s : mp_float;
i : integer;
begin
mpf_init2(v, w);
mpf_init3(tmp, tmp0, s);
mpf_set1(v); // 1
mpf_set_int(tmp, NB); // tmp=NB
while mpf_is_lt(x, tmp) do begin
mpf_mul(v, x, v); // v = v * x
mpf_add(x, one, x); // x = x + 1
end;
mpf_mul(x, x, tmp); // x^2
mpf_div(one, tmp, w); // w = 1 / x^2
mpf_set0(s); // s = 0
for i := NB downto 1 do begin
mpf_add(s, BM[i], tmp); // tmp = s + B[i]
mpf_mul(tmp, w, s); // s = tmp * w
end;
mpf_add(s, BM[0], tmp); // tmp = s + B[0]
mpf_div(tmp, x, s); // (s + B[0])/x
mpf_add(s, log_2pis2, s); // s = s + ln(2π)/2
mpf_ln(v, tmp); // ln(v)
mpf_sub(s, tmp, s); // s := s - ln(v)
mpf_sub(s, x, s); // s := s - x
mpf_div(one, two, tmp); // tmp = 1/2
mpf_sub(x, tmp, tmp0); // tmp0 = x - 1/2
mpf_ln(x, tmp); // ln(x)
mpf_mul(tmp0, tmp, tmp0); // tmp0 = (x - 1/2) * ln(x)
mpf_add(s, tmp0, ans); // ans = s + (x - 1/2) * ln(x)
mpf_clear2(v, w);
mpf_clear3(tmp, tmp0, s);
end;
// 多倍長ガンマ
// xの値が 0 と負整数の時Γは∞になるのですが処理をしていませんのでエラーになります。
// ケルビンの次数が整数の時は使用されません。
procedure gammaMul(var x, ans: mp_float);
var
tmp, tmp0, logG : mp_float;
begin
mpf_init3(tmp, tmp0, logG);
if mpf_is_lt(x, zero) then begin
mpf_mul(pai, x, tmp); // x*π
mpf_sin(tmp, tmp0); // sin(πx);
mpf_sub(one, x, tmp); // 1-x
log_GammaMul(tmp, logG); // loggamma(1-x);
mpf_exp(logG, logG); // exp(logG)
mpf_div(pai, tmp0, tmp); // π/sin(πx)
mpf_div(tmp, logG, ans); // ans = π/(sin(πx) * logG(1-x))
end
else begin
log_GammaMul(x, logG); // logG
mpf_exp(logG, ans); // exp(logG)
end;
mpf_clear3(tmp, tmp0, logG);
end;
// ディガンマ +整数のみ 多倍長
procedure digammaMUL(n: integer; var ans : mp_float);
var
s, tmp : mp_float;
k : integer;
begin
mpf_init2(s, tmp);
n := n - 1;
mpf_set0(s); // Σ=0
mpf_set0(tmp);
if n >= 0 then begin
for k := 1 to n do begin
mpf_set_int(tmp, k);
mpf_div(one, tmp, tmp); // 1 / k
mpf_add(s, tmp, s);
end;
end;
mpf_sub(s, gamma, ans); // Σ + γ
mpf_clear2(s, tmp);
end;
//------------------------------------------------------------------------------
// 階乗 多倍長
procedure factorialMul(n : integer; var ans: mp_float);
label
EXT;
var
i : integer;
bi: mp_float;
begin
mpf_init(bi);
mpf_set1(ans); // 1
mpf_add(one, one, bi); // bi = 2
if n <= 1 then begin // n <= 1 ans = 1
goto EXT;
end;
for i := 2 to n do begin // n!
mpf_mul(ans, bi, ans); // ans = ans * bi
mpf_add(bi, one, bi); // bi + 1
end;
EXT:
mpf_clear(bi);
end;
//--------------------------------- 非整数計算 -------------------------------
var
rk, ik : double; // x=0 で、無限大時の値
//------------------- complex power --------------------------------------------
procedure mpc_powa(x, y : mp_complex; var ans : mp_complex);
var
ay, ai, zero, harf, two : mp_float;
begin
mpf_init5(ay, ai, zero, harf, two);
mpc_pow(x, y, ans); // exp(y*ln(x))
// xの虚数部とyの虚数部0なら
if mpf_is0(x.im) and mpf_is0(y.im) then begin
mpf_set0(zero); // 0
mpf_set_int(two, 2); // 2
mpf_inv(two, harf); // 1/2 0.5
mpf_abs(y.re, ay); // yの実数部の絶対値
mpf_frac(ay, ai); // yの実数部の絶対値の小数部
mpf_sub(ai, harf, ai); // yの実数部の絶対値の小数部と0.5の差分
// 差分がゼロ(yの実数部の小数部が0.5)
if mpf_is0(ai) then
// xの実数部が0と等しいか0より大きいなら
if mpf_is_ge(x.re, zero) then mpf_set0(ans.im) // 答えの虚数部0
// 0より小さいなら
else mpf_set0(ans.re); // 答えの実数部0
mpf_frac(y.re, ai);
if mpf_is0(ai) then mpf_set0(ans.im);
end;
mpf_clear5(ay, ai, zero, harf, two);
end;
// 第一種変形ベッセル関数
// 非整数多倍長で計算
// xs2 = x / 2
procedure sigumaaIaxMul(var v : mp_float; var xs2, ri : mp_complex);
var
k : integer;
khg : mp_float;
s, x24k, tmp, tmp0, xei: mp_complex;
sb, xei2 : mp_complex;
tmf0 : mp_float;
begin
mpc_init5(s, x24k, tmp, tmp0, xei);
mpc_init2(sb, xei2);
mpf_init(khg);
mpf_init(tmf0);
mpc_set0(s); // Σ=0
mpc_set0(sb); // Σ=0
mpc_copy(xs2, xei);
mpc_mul(xei, xei, xei2); // xei^2
mpc_set1(x24k);
for k := 0 to KMV do begin
if mpf_is_ge(v, zero) then
mpf_copy(PVG[k], tmf0) // v > 0 Γ(v+k+1)
else
mpf_copy(MVG[k], tmf0); // v <=0 Γ(v+k+1)
mpf_mul(FA[k], tmf0, khg); // k!Γ(n+k+1)
// mpf_set_int(tmf, K + K); // 2k
// mpc_set_mpf(kc, tmf, zero); // kc = 2k + 0i 複素数
// mpc_powa(xei, kc, x24k); // (i(x^2)/4)^k
mpc_div_mpf(x24k, khg, tmp0); // ((i(x^2)/4)^k)/(k!Γ(v+k+1)) vkが0,負の整数の時±∞
mpc_add(s, tmp0, s); // Σ
mpc_sub(s, sb, tmp0);
if mpc_is0(tmp0) then break;
mpc_copy(s, sb);
mpc_mul(x24k, xei2, x24k);
end;
if mpf_is_ge(v, zero) or not mpc_is0(xei) then begin // v がゼロより大きいか xがゼロでない時
mpc_set_mpf(tmp, v, zero); // v + 0i
mpc_powa(xei, tmp, tmp0); // ((xe^(iπ/4)) /2)^V
mpc_mul(s, tmp0, s); // Σ
end;
mpc_copy(s, ri);
mpc_clear5(s, x24k, tmp, tmp0, xei);
mpc_clear2(sb, xei2);
mpf_clear(khg);
mpf_clear(tmf0);
end;
// 非整数 多倍長
// 第一種変形ベッセル関数の差分をsinで除算するため演算精度向上には大きな有効桁数が必要になります。
procedure ekazMul(var v : mp_float; var x, ri: mp_complex);
var
sv, sinvp, tmp : mp_float;
ipPv, imPv, sipv, tmpc : mp_complex;
begin
mpf_init3(sv, sinvp, tmp);
mpc_init4(ipPv, imPv, sipv, tmpc);
sigumaaIaxMul(v, x, ipPv); // ipv
mpf_chs(v, sv);
sigumaaIaxMul(sv, x, imPv); // imv
if not mpc_is0(x) then begin
mpc_sub(imPv, ipPv, sipv); // imv - ipv
mpf_mul(v, pai, tmp); // v * π
mpf_sin(tmp, tmp); // sin(v * pi)
mpc_div_mpf(sipv, tmp, sipv); // (imv - ipv)/sin(v * pi)
mpf_div(pai, two, tmp); // π /2
mpc_mul_mpf(sipv, tmp, ri); // (Imv - Ipv) / sin(v * pi) * pi / 2
end;
mpf_clear3(sv, sinvp, tmp);
mpc_clear4(ipPv, imPv, sipv, tmpc);
end;
//---------------------------整数計算-------------------------------------------
// 整数 多倍長計算
// 計算精度の向上には、Σの最大値のUPと演算有効桁数のUPとなります。
procedure knzMul(var v : mp_float; var z, ri : mp_complex);
var
a, b, c, inz, zc : mp_complex;
z2, knza, z24, mz24: mp_complex;
tmp, tmp0, tmp1 : mp_complex;
n, mone : mp_float;
mf, nnf, tmf, tmf0 : mp_float;
tmf1, nb : mp_float;
k, m, nn : integer;
inzb, ab, cb : mp_complex;
begin
if mpc_is0(z) then begin // z = 0 の時は±∞となるので計算しない
mpc_set0(ri);
exit;
end;
mpc_init5(a, b, c, inz, zc);
mpc_init4(z2, knza, z24, mz24);
mpc_init3(tmp, tmp0, tmp1);
mpf_init2(n, mone);
mpf_init4(mf, nnf, tmf, tmf0);
mpf_init2(tmf1, nb);
mpc_init3(inzb, ab, cb);
mpf_copy(v, nb);
mpf_abs(v, n);
nn := abs(round(mpf_todouble(n)));
mpf_chs(one, mone);
mpc_copy(z, z2); // z -> z2
mpc_mul(z2, z2, z24); // (z/2)^2
// mpc_chs(z24, mz24); // -(z/2)^2
// form1.memo1.Lines.Append('z/2 =' + string(mpf_decimal_alt(z24.im, 50)));
mpc_set0(inz);
mpc_set0(inzb);
mpc_set1(mz24);
// Inz
for m := 0 to KMV do begin
mpf_mul(FA[m], FA[m + nn], tmf);
mpf_set_int(mf, m);
mpc_set_mpf(tmp0, mf, zero);
// mpc_pow(z24, tmp0, tmp1);
mpc_div_mpf(tmp1, tmf, tmp0);
mpc_add(inz, tmp0, inz);
mpc_sub(inz, inzb, tmp0);
if mpc_is0(tmp0) then break;
mpc_copy(inz, inzb);
mpc_mul(mz24, z24, mz24);
end;
// form1.memo1.Lines.Append('lnz = ' + string(mpf_decimal_alt(inz.im, 50)));
mpf_set_int(nnf, nn);
mpc_set_mpf(tmp0, nnf, zero);
mpc_pow(z2, tmp0, tmp);
mpc_mul(inz, tmp, inz);
// form1.memo1.Lines.Append( string(mpf_decimal_alt(inz.im, 50)));
// a
mpc_set0(a);
mpc_set0(ab);
mpc_set1(mz24);
for k := 0 to nn - 1 do begin
mpf_div(FA[nn - k - 1], FA[k], tmf);
mpc_set_mpf(tmp0, tmf, zero);
// mpf_set_int(kf, k);
// mpc_set_mpf(tmp1, kf, zero);
// mpc_pow(z24, tmp1, tmp1);
mpc_mul(tmp0, tmp1, tmp);
if k mod 2 <> 0 then mpc_chs(tmp, tmp);
mpc_add(a, tmp, a);
mpc_sub(a, ab, tmp);
if mpc_is0(tmp) then break;
mpc_copy(a, ab);
mpc_mul(mz24, z24, mz24);
end;
// form1.memo1.Lines.Append('a 1= ' + string(mpf_decimal_alt(a.im, 50)));
mpf_set_int(nnf, -nn);
if mpf_is0(z2.im) then begin
mpf_abs(z2.re, tmf);
mpf_expt(tmf, nnf, tmf);
mpc_set_mpf(tmp, tmf, zero);
if mpf_is_lt(z2.re, zero) then mpc_chs(tmp, tmp);
end
else begin
mpc_set_mpf(tmp1, nnf, zero);
mpc_pow(z2, tmp1, tmp);
end;
mpc_mul(a, tmp, tmp0);
mpc_div_mpf(tmp0, two, a);
// form1.memo1.Lines.Append('a2= ' + string(mpf_decimal_alt(a.im, 50)));
// b
if (nn + 1) mod 2 = 0 then
mpc_set_mpf(tmp1, one, zero)
else
mpc_set_mpf(tmp1, mone, zero);
mpc_ln(z2, tmp0);
mpc_mul(tmp1, tmp0, tmp);
mpc_mul(tmp, inz, b);
// form1.memo1.Lines.Append( string(mpf_decimal_alt(b.re, 50)));
// c
mpc_set0(c);
mpc_set0(cb);
mpc_set1(mz24);
for k:= 0 to KMV do begin
mpf_add(DG[k + 1], DG[nn + k + 1], tmf);
mpf_mul(FA[k], FA[nn + k], tmf0);
// mpf_set_int(kf, k);
// mpc_set_mpf(tmp, kf, zero);
// mpc_pow(z24, tmp, tmp);
mpc_mul_mpf(tmp, tmf, tmp);
mpc_div_mpf(tmp, tmf0,tmp);
mpc_add(c, tmp, c);
mpc_sub(c, cb, tmp);
if mpc_is0(tmp) then break;
mpc_copy(c, cb);
mpc_mul(mz24, z24, mz24);
end;
// c := c * power(-1, nn) / 2 * varcomplexpower(z2, nn);
mpf_set_int(nnf, nn);
mpc_set_mpf(tmp0, nnf, zero);
mpc_pow(z2, tmp0, tmp1); // z2^n
mpc_mul(c, tmp1, tmp); // c * z2^n
if nn mod 2 = 0 then // -1^nn
mpc_set_mpf(tmp1, one, zero)
else
mpc_set_mpf(tmp1, mone, zero);
mpc_div_mpf(tmp1, two, tmp0); // (-1~n)/2
mpc_mul(tmp, tmp0, c); // c := z2^n * c * (-1~n)/2
// knza := a + b + c;
mpc_add(a, b, tmp);
mpc_add(tmp, c, knza);
mpf_div(n, two, tmf); // n / 2
mpf_int(tmf, tmf0); // int(n / 2)
mpf_sub(tmf, tmf0, tmf); // n / 2 - int(n / 2)
// nがゼロ以下で偶数だったら
if mpf_is_lt(nb, zero) and mpf_is_ne(tmf, zero) then // -1^n
mpc_chs(knza, ri) // 奇数時
else
mpc_copy(knza, ri); // 偶数時
mpc_clear5(a, b, c, inz, zc);
mpc_clear4(z2, knza, z24, mz24);
mpc_clear3(tmp, tmp0, tmp1);
mpf_clear2(n, mone);
mpf_clear4(mf, nnf, tmf, tmf0);
mpf_clear2(tmf1, nb);
mpc_clear3(inzb, ab, cb);
end;
// akima m,t テーブル作成
// x[] xデーター配列
// y[] yデーター配列
// m[] m係数テーブル
// t[] t係数テーブル
procedure akima_table;
var
ii, n : integer;
a, b, half, tmf, tmf0 : mp_float;
ytm, xtm : array of mp_float;
tmf1 : mp_float;
begin
n := high(xt) + 1;
setlength(ytm, n);
setlength(xtm, n);
for ii := 0 to n - 1 do begin
mpf_init(ytm[ii]);
mpf_init(xtm[ii]);
end;
mpf_init5(a, b, half, tmf, tmf0);
mpf_init(tmf1);
mpf_set_dbl(half, 1 / 2);
// mpf_set_int(tow, 2);
// mpf_set0(zero);
for ii := 0 to n -1 do begin
mpf_set_dbl(xtm[ii], xt[ii]);
mpf_set_dbl(ytm[ii], yt[ii]);
end;
// shift data by + 2 in the array and compute the secants
// also calculate extrapolated and end point secants
// 傾斜α両端を除く Δy/Δx
for ii := 0 to n - 2 do begin
mpf_sub(ytm[ii + 1], ytm[ii], tmf);
mpf_sub(xtm[ii + 1], xtm[ii], tmf0);
mpf_div(tmf, tmf0, m[ii + 2]);
end;
// for ii := 0 to n - 2 do
// m[ii + 2] := (yt[ii + 1] - yt[ii]) / (xt[ii + 1] - xt[ii]);
// 端点傾斜処理
mpf_mul(two, m[2], tmf);
mpf_sub(tmf, m[3], m[1]);
// m[1] := 2 * m[2] - m[3];
mpf_mul(two, m[1], tmf);
mpf_sub(tmf, m[2], m[0]);
// m[0] := 2 * m[1] - m[2];
mpf_mul(two, m[n], tmf);
mpf_sub(tmf, m[n - 1], m[n + 1]);
// m[n + 1] := 2 * m[n] - m[n - 1];
mpf_mul(two, m[n + 1], tmf);
mpf_sub(tmf, m[n], m[n + 2]);
// m[n + 2] := 2 * m[n + 1] - m[n];
// 各ポイントの傾斜係数計算
for ii := 0 to n - 1 do begin
mpf_sub(m[ii + 3],m[ii + 2],tmf0);
mpf_abs(tmf0, a);
// a := abs(m[ii + 3] - m[ii + 2]);
mpf_sub(m[ii + 1], m[ii], tmf0);
mpf_abs(tmf0, b);
// b := abs(m[ii + 1] - m[ii]);
mpf_add(a, b, tmf1);
if mpf_is_ne(tmf1, zero) then begin
mpf_mul(a, m[ii + 1], tmf);
mpf_mul(b, m[ii + 2], tmf0);
mpf_add(tmf, tmf0, tmf);
mpf_div(tmf, tmf1, t[ii]);
end
else begin
mpf_add(m[ii + 2], m[ii + 1], tmf);
mpf_mul(half, tmf, t[ii]);
end;
{
if (a + b) <> 0 then begin
t[ii] := (a * m[ii + 1] + b * m[ii + 2]) / (a + b);
end
else
t[ii] := half * (m[ii + 2] + m[ii + 1]);
}
end;
for ii := 0 to n - 1 do begin
mpf_clear(ytm[ii]);
mpf_clear(xtm[ii]);
end;
mpf_clear5(a, b, half, tmf, tmf0);
mpf_clear(tmf1);
end;
// akima 補間値計算
// xx xの値
// x[] xデーター配列
// y[] yデーター配列
// m[] m係数テーブル
// t[] t係数テーブル
// result 補間値y'
function akima_Interpolation(xx: double): double;
var
iB, iM, iT: integer;
a, b, tmf, tmf0 : mp_float;
c, d, e, f, tmf1 : mp_float;
three : mp_float;
begin
mpf_init4(a, b, tmf, tmf0);
mpf_init5(c, d, e, f, tmf1);
mpf_init(three);
mpf_set_int(three, 3);
iB := low(xt); // x[] bottom 配列no
iT := high(xt); // x[] top配列No
// xx値の上下の配列xの配列番号を探す
// XX<x[iB]の場合一番下の区間 XX>x[iT]の場合一番上の区間
while (iT - iB) > 1 do begin
iM := (iB + iT) div 2; // middle配列no
if xt[iM] > xx then
iT := iM
else
iB := iM;
end;
mpf_set_dbl(b, xt[iT] - xt[iB]);
// b := xt[iT] - xt[iB]; // 区間のxの変化量
mpf_set_dbl(a, xx - xt[iB]);
// a := xx - xt[iB]; // x[iB]からのxの値
// 3次akima spline 計算
mpf_set_dbl(c, yt[iB]); // c = yt[ib]
mpf_mul(t[iB], a, d); // d = t[ib] * a
mpf_mul(three, m[iB + 2], tmf); // 3 * m[iB + 2]
mpf_mul(two, t[ib], tmf0); // 2 * t[iB]
mpf_sub(tmf, tmf0, tmf1); // 3 * m[iB + 2] - 2 * t[iB]
mpf_sub(tmf1, t[iB + 1], tmf); // 3 * m[iB + 2] - 2 * t[iB] - t[iB + 1]
mpf_mul(tmf, a, tmf); // (3 * m[iB + 2] - 2 * t[iB] - t[iB + 1]) * a
mpf_mul(tmf, a, tmf); // (3 * m[iB + 2] - 2 * t[iB] - t[iB + 1]) * a * a
mpf_div(tmf, b, e); // (3 * m[iB + 2] - 2 * t[iB] - t[iB + 1]) * a * a / b
mpf_add(t[iB], t[iB + 1], tmf); // t[iB] + t[iB + 1]
mpf_mul(two, m[iB + 2], tmf0); // 2 * m[iB + 2]
mpf_sub(tmf, tmf0, tmf); // t[iB] + t[iB + 1] - 2 * m[iB + 2]
mpf_mul(tmf, a, tmf); // (t[iB] + t[iB + 1] - 2 * m[iB + 2]) * a
mpf_mul(tmf, a, tmf); // (t[iB] + t[iB + 1] - 2 * m[iB + 2]) * a * a
mpf_mul(tmf, a, tmf); // (t[iB] + t[iB + 1] - 2 * m[iB + 2]) * a * a * a
mpf_mul(b, b, tmf0); // b * b
mpf_div(tmf, tmf0, f); // (t[iB] + t[iB + 1] - 2 * m[iB + 2]) * a * a * a / (b * b)
mpf_add(c, d, tmf); // c + d
mpf_add(tmf, e, tmf); // c + d + e
mpf_add(tmf, f, tmf); // c + d + e + f
result := mpf_todouble(tmf);
{
result := yt[iB]
+ t[iB] * a
+ (3 * m[iB + 2] - 2 * t[iB] - t[iB + 1]) * a * a / b
+ (t[iB] + t[iB + 1] - 2 * m[iB + 2]) * a * a * a / (b * b);
}
mpf_clear4(a, b, tmf, tmf0);
mpf_clear5(c, d, e, f, tmf1);
mpf_clear(three);
end;
procedure TForm1.chart1coment;
begin
Chart1.Canvas.Font.Size := 8;
Chart1.Canvas.Font.Style := [];
chart1.Canvas.Font.Color := clred;
chart1.Canvas.TextOut(chart1.Width - 30, 1,'実数');
chart1.Canvas.Font.Color := clblue;
chart1.Canvas.TextOut(chart1.Width - 30, 13,'虚数');
chart1.Canvas.Pen.Width := 1;
chart1.Canvas.Pen.Color := clred;
chart1.Canvas.MoveTo(chart1.Width - 50, 6);
chart1.Canvas.LineTo(chart1.Width - 32, 6);
chart1.Canvas.Pen.Color := clblue;
chart1.Canvas.MoveTo(chart1.Width - 50, 18);
chart1.Canvas.LineTo(chart1.Width - 32, 18);
end;
//------------------------------------------------------------------------------
// ta[] グラフ用計算点配列
procedure TForm1.Button1Click(Sender: TObject);
label
EXT;
const
ta : array[0..GL - 1] of double = (0.08, 0.13, 0.23, 0.46, 0.86, 1.68, 2.7, 4);
YPM = 1E304; // double の最大値制限 オーバーフロー対策
YMM = - YPM;
var
ch, i, xi: integer;
kerx, keix: double;
kerxe, keixe: double;
x, v, xv, ia : double;
xmin, xmax, dx, dxf: double;
ymin, ymax: double;
xm, vm, ndm, dxm: mp_float;
avm, andm: mp_float;
tmp : mp_float;
xc, epc, ri, tmc : mp_complex;
berl : Darray;
beil : Darray;
beru : Darray;
beiu : Darray;
xl : Darray;
xu : Darray;
vmaxmes : string;
GCF : integer;
StopWatch : TStopwatch;
ElapsedMillseconds : Int64;
mm, ss, ms : integer;
k : integer;
vk, tmf, tmf0, iam : mp_float;
GU, GS : integer;
// xの値複素数に変換
procedure xtoxc(var x, ia : mp_float; var xc : mp_complex);
begin
mpc_set_mpf(xc, x, ia); // xc
mpc_div_mpf(xc, two, xc); // xc/2
end;
// doubleの最大値の制限
function maxmin(x : double): double;
begin
result := x;
if x > YPM then result := YPM;
if x < YMM then result := YMM;
end;
begin
memo1.Clear;
val(labelededit1.Text, v, ch);
if ch <> 0 then begin
application.MessageBox('次数vの値に間違いがあります。','注意', 0);
exit;
end;
if abs(v) > vmax then begin
vmaxmes := 'Vの値は ±' + intTostr(vmax) + '以下にして下さい。';
application.MessageBox(pwideChar(vmaxmes),'注意', 0);
exit;
end;
val(labelededit2.Text, x, ch);
if ch <> 0 then begin
application.MessageBox('xの値に間違いがあります。','注意', 0);
exit;
end;
if abs(x) > 100 then begin
vmaxmes := 'xの値は±100迄にしてください';
application.MessageBox(pchar(vmaxmes),'注意', 0);
exit;
end;
val(labelededit2.Text, x, ch);
if ch <> 0 then begin
application.MessageBox('xの値に間違いがあります。','注意', 0);
exit;
end;
if abs(x) > 100 then begin
vmaxmes := 'xの値は±100迄にしてください';
application.MessageBox(pchar(vmaxmes),'注意', 0);
exit;
end;
val(labelededit3.Text, ia, ch);
if ch <> 0 then begin
application.MessageBox('i の値に間違いがあります。','注意', 0);
exit;
end;
if abs(ia) > 100 then begin
vmaxmes := 'i の値は±100迄にしてください';
application.MessageBox(pchar(vmaxmes),'注意', 0);
exit;
end;
KMV := KMmax; // Σ 0～kMAX
mpf_init4(vm, xm, ndm, dxm);
mpf_init2(avm, andm);
mpf_init(tmp);
mpf_init4(vk, tmf, tmf0, iam);
mpc_init4(xc, epc, ri, tmc);
mpf_read_decimal(vm, PAnsiChar(ansistring(labelededit1.Text + #00)));
mpf_read_decimal(xm, PAnsiChar(ansistring(labelededit2.Text + #00)));
mpf_read_decimal(iam, PAnsiChar(ansistring(labelededit3.Text + #00)));
rk := 0;
ik := 0;
memo1.Clear;
mpf_int(vm, ndm);
mpf_sub(vm, ndm, ndm); // 整数ならndm = 0
mpf_abs(ndm, andm);
// Γ値配列計算
mpf_abs(vm, avm);
if mpf_is_ne(ndm, zero) then begin // 次数vの値が非整数の時計算
for k := 0 to KMV do begin
mpf_set_int(tmf, k); // k
mpf_add(tmf, avm, tmf0); // v + k
mpf_add(tmf0, one, vk); // vk= v + k + 1
gammaMul(vk, PVG[k]); // Γ(n+k+1)
end;
mpf_chs(avm, avm); // -v
for k := 0 to KMV do begin
mpf_set_int(tmf, k); // k
mpf_add(tmf, avm, tmf0); // -v + k
mpf_add(tmf0, one, vk); // vk= -v + k + 1
gammaMul(vk, MVG[k]); // Γ(n+k+1)
end;
end;
mpf_read_decimal(dxm, PAnsiChar(ansistring('1E-10' + #00)));
if mpf_is_lt(andm, dxm) and mpf_is_ne(ndm, zero) then begin
application.MessageBox('次数vの値の小数部は 1E-10 より大きくしてください。','注意', 0);
goto EXT;
end;
// ゼロ+側近辺
mpf_read_decimal(dxm, PAnsiChar(ansistring('1E-50' + #00)));
mpf_abs(vm, avm);
xToxc(dxm, iam, xc);
if mpf_is_ne(ndm, zero) then
ekazMul(avm, xc, ri)
else
knzMul(avm, xc, ri);
if mpf_is_ge(ri.re, zero) then rk := infinity
else rk := -infinity;
if mpf_is_ge(ri.im, zero) then ik := infinity
else ik := -infinity;
memo1.Lines.Append('v = ' + floatTostr(v) + ' x = ' + floatTostr(x));
StopWatch := TStopwatch.StartNew;
// 表示値の計算
kerxe := 0;
keixe := 0;
// x <> 0
xToxc(xm, iam, xc);
if not mpc_is0(xc) then begin
if mpf_is_ne(ndm, zero) then
ekazMul(avm, xc, ri)
else
knzMul(avm, xc, ri);
{ if mpf_is0(xc.im) then begin // mpc_pow の問題対策
mpf_frac(avm, tmf);
mpf_inv(two, tmf0);
mpf_sub(tmf, tmf0, tmf);
if mpf_is0(tmf) then
if mpf_is_ge(xc.re,zero) then mpf_set0(ri.im)
else mpf_set0(ri.re);
end; }
memo1.Lines.Append('kv(x) = ' + string(mpf_decimal(ri.re, 50)));
if mpf_is_ge(ri.im, zero) then
memo1.Lines.Append(' = +' + string(mpf_decimal(ri.im, 50)) + ' i')
else
memo1.Lines.Append(' = ' + string(mpf_decimal(ri.im, 50)) + ' i');
kerxe := mpf_todouble(ri.re);
keixe := mpf_todouble(ri.im);
end
// x = 0
else begin
memo1.Lines.Append('kv(x) = INF');
memo1.Lines.Append(' = +0i');
kerxe := rk;
keixe := 0;
end;
StopWatch.Stop;
ElapsedMillseconds := StopWatch.ElapsedMilliseconds;
// goto EXT;
ms := ElapsedMillseconds * (GL + 1) * 2 + 2000;
mm := ms div 60000;
ss := (ms mod 60000) div 1000;
vmaxmes := 'グラフ表示に約' + inttostr(mm) + '分' + inttostr(ss) + '秒必要です。';
memo1.Lines.Append(vmaxmes);
series1.Clear;
series2.Clear;
series3.Clear;
series4.Clear;
series5.Clear;
series6.Clear;
application.ProcessMessages;
if (checkbox2.Checked = true) then begin // グラフ無だったら終了
Chart1.Canvas.Font.Style := [fsBold];
Chart1.Canvas.Font.size := 8;
Chart1.Canvas.TextOut(170, 115,'グラフ無し');
goto EXT;
end;
if ElapsedMillseconds > 500 then begin
vmaxmes := vmaxmes + #13#10 + 'グラフの表示をしますか?';
if MessageDlg(vmaxmes , mtConfirmation, [mbYes, mbNo], 0, mbYes) = mrNo then begin
Chart1.Canvas.Font.Style := [fsBold];
Chart1.Canvas.Font.size := 8;
Chart1.Canvas.TextOut(170, 115,'グラフ無し');
goto EXT;
end;
end;
// 最大値最小値の検索とグラフデーター作成
xi := round(x);
xmin := xi - 4;
GCF := 0;
if (x >= -2) and (x <= 2) then GCF := 1;
if (x >= -3) and (x <= -2) then GCF := 2;
if (x >= 2) and (x <= 3) then GCF := 3;
if (x >= -4) and (x <= -3) then GCF := 4;
if (x >= 3) and (x <= 4) then Gcf := 5;
case GCF of
0: xmin := xi - 4;
1: xmin := -4;
2: xmin := -5;
3: xmin := -3;
4: xmin := -6;
5: xmin := -2;
end;
xmax := xmin + 8;
case GCF of
0 : begin
setlength(berl, GL + GL);
setlength(beil, GL + GL);
setlength(xt, GL + GL); setlength(yt, GL + GL);
setlength(xl, GL + GL);
end;
1, 2, 3, 4, 5:
begin
setlength(berl, GL); setlength(beru, GL);
setlength(beil, GL); setlength(beiu, GL);
setlength(xt, GL); setlength(yt, GL);
setlength(xl, GL); setlength(xu, GL);
end;
end;
dxf := 0.1;
dx := dxf;
GS := 40;
GU := 40;
ch := GCF;
case GCF of
0 :
begin
dx := (xmax - xmin) / (Gl + GL - 1);
for i := 0 to GL + GL - 1 do xl[i] := dx * i + xmin;
xl[0] := xl[0] + dxf;
xl[GL + GL - 1] := xl[GL + GL - 1] - dxf;
GS := 80;
end;
1 :
begin
for i := 0 to GL - 1 do begin
xu[i] := ta[i];
xl[GL - i - 1] := -ta[i];
end;
end;
else // 2,3,4,5
begin
for i := 0 to GL - 1 do begin
xu[i] := ta[i];
xl[GL - i - 1] := -ta[i];
end;
case ch of
2 : begin dx := 5 / 4; dxf := 3 / 4; GS := 50; GU := 30; end;
3 : begin dx := 3 / 4; dxf := 5 / 4; GS := 30; GU := 50; end;
4 : begin dx := 6 / 4; dxf := 2 / 4; GS := 60; GU := 20; end;
5 : begin dx := 2 / 4; dxf := 6 / 4; GS := 20; GU := 60; end;
end;
for i := 0 to Gl - 1 do begin
xl[i] := xl[i] * dx;
xu[i] := xu[i] * dxf;
end;
end;
end;
// グラフ用データー作成
ymin := 0;
ymax := 0;
case GCF of
0 : begin
for i := 0 to GL + GL - 1 do begin
xv := xl[i];
mpf_set_dbl(tmp, xv);
xToxc(tmp, iam, xc);
if mpf_is_ne(ndm, zero) then
ekazMul(avm, xc, ri)
else
knzMul(avm, xc, ri);
berl[i] := maxmin(mpf_todouble(ri.re));
beil[i] := maxmin(mpf_todouble(ri.im));
if berl[i] > ymax then ymax := berl[i];
if beil[i] > ymax then ymax := beil[i];
if berl[i] < ymin then ymin := berl[i];
if beil[i] < ymin then ymin := beil[i];
end;
end;
1, 2, 3, 4, 5:
for i := 0 to GL - 1 do begin
xv := xl[i];
mpf_set_dbl(tmp, xv);
xToxc(tmp, iam, xc);
if mpf_is_ne(ndm, zero) then
ekazMul(avm, xc, ri)
else
knzMul(avm, xc, ri);
berl[i] := maxmin(mpf_todouble(ri.re));
beil[i] := maxmin(mpf_todouble(ri.im));
if berl[i] > ymax then ymax := berl[i];
if beil[i] > ymax then ymax := beil[i];
if berl[i] < ymin then ymin := berl[i];
if beil[i] < ymin then ymin := beil[i];
xv := xu[i];
mpf_set_dbl(tmp, xv);
xToxc(tmp, iam, xc);
if mpf_is_ne(ndm, zero) then
ekazMul(avm, xc, ri)
else
knzMul(avm, xc, ri);
beru[i] := maxmin(mpf_todouble(ri.re));
beiu[i] := maxmin(mpf_todouble(ri.im));
if beru[i] > ymax then ymax := beru[i];
if beiu[i] > ymax then ymax := beiu[i];
if beru[i] < ymin then ymin := beru[i];
if beiu[i] < ymin then ymin := beiu[i];
end;
end;
if kerxe > ymax then kerxe := ymax;
if kerxe < ymin then kerxe := ymin;
if keixe > ymax then keixe := ymax;
if keixe < ymin then keixe := ymin;
series3.AddXY(x, kerxe);
series4.AddXY(x, keixe);
if checkbox1.Checked = true then
case GCF of
0:
begin
for i := 0 to GL + GL - 1 do begin
series1.AddXY(xl[i], berl[i]);
series2.AddXY(xl[i], beil[i]);
end;
end;
1, 2, 3, 4, 5 :
begin
for i := 0 to GL - 1 do begin
series1.AddXY(xl[i], berl[i]);
series2.AddXY(xl[i], beil[i]);
series5.AddXY(xu[i], beru[i]);
series6.AddXY(xu[i], beiu[i]);
end;
end;
end;
if checkbox1.Checked = false then
// グラフ表示
case GCF of
0:
begin
for i := 0 to GL + GL - 1 do begin
xt[i] := xl[i];
yt[i] := berl[i];
end;
akima_table;
dx := (xt[GL + GL - 1] - xt[0]) / GS;
for i := 0 to GS do begin
xv := dx * i + xt[0];
kerx := maxmin(akima_Interpolation(xv));
series1.AddXY(xv, kerx);
end;
for i := 0 to GL + GL - 1 do yt[i] := beil[i];
akima_table;
for i := 0 to GS do begin
xv := dx * i + xt[0];
keix := maxmin(akima_Interpolation(xv));
series2.AddXY(xv, keix);
end;
end;
1, 2, 3, 4, 5 :
begin
for i := 0 to GL- 1 do begin
xt[i] := xl[i];
yt[i] := berl[i];
end;
akima_table;
dx := xt[0] / GS;
for i := GS downto 1 do begin
xv := dx * i;
kerx := maxmin(akima_Interpolation(xv));
series1.AddXY(xv, kerx);
end;
for i := 0 to GL- 1 do yt[i] := beil[i];
akima_table;
for i := GS downto 1 do begin
xv := dx * i;
keix := maxmin(akima_Interpolation(xv));
series2.AddXY(xv, keix);
end;
if mpf_is0(xm) then begin
// series1.AddXY(0, kerxe);
// series2.AddXY(0, keixe);
series5.AddXY(0, kerxe);
series6.AddXY(0, keixe);
end;
for i := 0 to GL- 1 do begin
xt[i] := xu[i];
yt[i] := beru[i];
end;
akima_table;
dx := xt[GL - 1] / GU;
for i := 1 to GU do begin
xv := dx * i;
kerx := maxmin(akima_Interpolation(xv));
series5.AddXY(xv, kerx);
end;
for i := 0 to GL- 1 do yt[i] := beiu[i];
akima_table;
for i := 1 to GU do begin
xv := dx * i;
keix := maxmin(akima_Interpolation(xv));
series6.AddXY(xv, keix);
end;
end;
end;
application.ProcessMessages;
chart1coment;
EXT:
mpf_clear4(vm, xm, ndm, dxm);
mpf_clear2(avm, andm);
mpf_clear(tmp);
mpf_clear4(vk, tmf, tmf0, iam);
mpc_clear4(xc, epc, ri, tmc);
end;
procedure TForm1.FormCreate(Sender: TObject);
var
i : integer;
N, D, tmp : mp_float;
begin
mpf_set_default_decprec(200); // 有効桁数200桁
setlength(BM, NB + 1); // ベルヌーイ数 配列
setlength(DG, KMmax + Vmax + 2); // ディガンマ
setlength(FA, KMmax + Vmax + 1); // 階乗
setlength(t, GL + GL); // akima 補間値計算 配列 t
setlength(m, GL + GL + 3); // akima 補間値計算 配列 m
setlength(PVG, KMmax + 1); // +vΓ
setlength(MVG, KMmax + 1); // -vΓ
for i := 0 to NB do mpf_init(BM[i]);
for i := 0 to KMmax + Vmax + 1 do mpf_init(DG[i]);
for i := 0 to KMmax + Vmax do mpf_init(FA[i]);
for i := 0 to KMmax do mpf_init(PVG[i]);
for i := 0 to KMmax do mpf_init(MVG[i]);
mpf_init3(N, D, tmp);
mpf_init(gamma);
mpf_init5(pai, zero, one, two, four);
mpf_init(log_2pis2);
mpf_set_pi(pai); // π
mpf_set0(zero); // 0
mpf_set1(one); // 1
mpf_set_int(two, 2); // 2
mpf_set_int(four, 4); // 4
mpf_mul(pai, two, tmp); // 2π
mpf_ln(tmp, tmp); // ln(2π)
mpf_div(tmp, two, log_2pis2); // ln(2π)/2
mpf_read_decimal(gamma, PAnsiChar(ansistring(gstr + #00))); // γ
for i := 0 to GL + GL - 1 do mpf_init(t[i]);
for i := 0 to GL + GL + 2 do mpf_init(m[i]);
Bernoulli_number_BigInteger; // ベルヌーイ数作成
for i := 0 to NB do begin
mpf_read_decimal(N, PAnsiChar(ansistring(NumeratorString[i] + #00)));
mpf_read_decimal(D, PAnsiChar(ansistring(DenominatorString[i] + #00)));
mpf_div(N, D, BM[i]);
end;
for i := 0 to KMmax + Vmax + 1 do begin
digammaMUL(i, D);
mpf_copy(D, DG[i]);
end;
for i := 0 to KMmax + Vmax do begin
factorialMul(i, N);
mpf_copy(N, FA[i]);
end;
memo1.Clear;
mpf_clear3(N, D, tmp);
end;
procedure TForm1.FormDestroy(Sender: TObject);
var
i : integer;
begin
for i := 0 to NB do mpf_clear(BM[i]);
for i := 0 to KMmax + Vmax + 1 do mpf_clear(DG[i]);
for i := 0 to KMmax + Vmax do mpf_clear(FA[i]);
for i := 0 to GL + GL - 1 do mpf_clear(t[i]);
for i := 0 to GL + GL + 2 do mpf_clear(m[i]);
for i := 0 to KMmax do mpf_clear(PVG[i]);
for i := 0 to KMmax do mpf_clear(MVG[i]);
mpf_clear(gamma);
mpf_clear5(pai, zero, one, two, four);
mpf_clear(log_2pis2);
end;
end.
Bessel2_function.zip