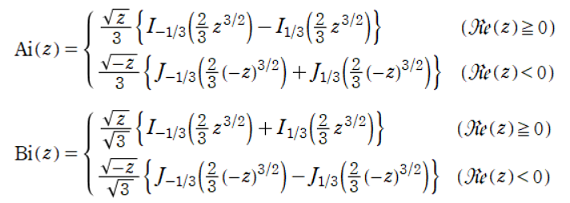
2024-05-07 一般エアリー関数 追加
エアリー関数
エアリー関数についての詳細は、ウィキペディアのエアリー関数を参照してください。
又、Airy function をwebで検索すれば沢山でてくるので、参考にしてください。
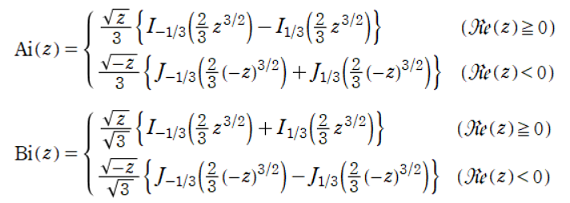
ウィキペディアでは、Ai(z)が、Kαで書かれているが、計算内容は、同じです。
ベッセル関数により計算されますが、:ベッセルの計算に階乗とΓ関数を使用し、級数計算の収束を行う為、グラフを作成する場合、計算に時間が掛かるので、グラフ作成はは近似計算で行います。
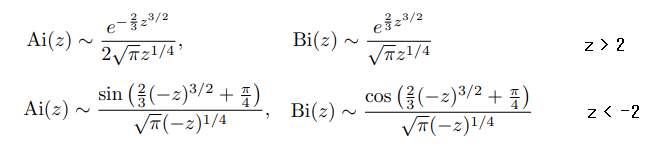
zの値が-2～2の間は、正規の計算で行い、それ以外の範囲は近似計算でグラフを作成します。
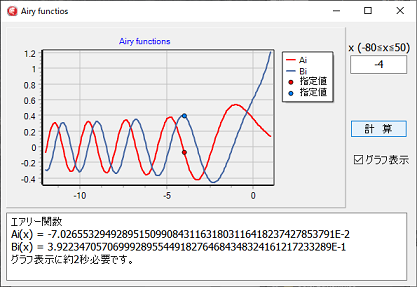プログラムの起動時に階乗とΓ配列を作成する為、お待ち画面が表示されますが、その後は表示されません。
ベッセル関数に与える次数(v)の値が1/3と固定されているのでΓ関数を先に計算しておきます。
このプログラムでは、xの値が、-80～50となっていますが、この範囲を狭くすれば、必要な配列の大きさを小さくすることが出来るのと、演算の桁数を下げる事が出来るので計算が速くなります。
計算結果の有効桁数50桁を保証する為、300桁の計算をしています。
大きな値の差分で、その差分が小さな値となる事があるので、計算結果の有効桁数に対して、何倍もの有効桁数が必要となります。
プログラム
プログラムには、二種類の多倍長計算が組み込んでありますが、組み込み方は第１種ケルビン関数ｖ，ｘ実数を参照して下さい。
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls,
VclTee.TeeGDIPlus, VCLTee.TeEngine, VCLTee.Series, VCLTee.TeeProcs,
VCLTee.Chart, System.Diagnostics;
type
TForm1 = class(TForm)
Button1: TButton;
Memo1: TMemo;
LabeledEdit2: TLabeledEdit;
Chart1: TChart;
Series1: TLineSeries;
Series2: TLineSeries;
Series3: TPointSeries;
Series4: TPointSeries;
CheckBox1: TCheckBox;
Timer1: TTimer;
procedure Button1Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure FormClose(Sender: TObject; var Action: TCloseAction);
procedure Timer1Timer(Sender: TObject);
private
{ Private 宣言 }
procedure Setting;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
uses system.Math, System.VarCmplx, Velthuis.BigIntegers,mp_real, mp_cmplx, mp_types, mp_base;
{$R *.dfm}
type
DArray = array of double;
var
BM : array of mp_float; // ベルヌーイ数配列
FA : array of mp_float; // 階乗配列
PVG : array of mp_float; // +VΓ
MVG : array of mp_float; // -VΓ
zero, one, two, four : mp_float;
three, pai, log_2pis2 : mp_float;
const
KMmax = 1000; // KM max 1000
//------------------------------------------------------------------------------
NB = 150; // ベルヌーイ数 配列数 NB + 1
var
NumeratorString : array[0..NB] of string; // 分子
DenominatorString : array[0..NB] of string; // 分母
// 最大公約数 ユークリッドの互除法 BigInteger
function gcd_BigInteger(x, y: BigInteger): BigInteger;
var
t : BigInteger;
begin
while y <> 0 do begin
t := x mod y;
x := y;
y := t;
end;
result := x;
end;
// ベルヌーイ数
// Akiyama-Tanigawa algorithm
// BigInteger
procedure Bernoulli_number_BigInteger;
const
n = (NB + 1) * 2;
var
m, j, k : integer;
a : array of BigInteger; // 分子
b : array of BigInteger; // 分母
tmpN : BigInteger; // 分子
tmpD : BigInteger; // 分母
gcd : BigInteger; // 最大公約数
b0 : BigInteger;
begin
setlength(a, n + 1);
setlength(b, n + 1);
k := 0;
for m := 0 to n do begin
a[m] := 1; // 分子 初期値
b[m] := (m + 1); // 分母 初期値
for j := m - 1 downto 0 do begin
tmpN := a[j] * b[j + 1] - a[j + 1] * b[j]; // 分子
tmpN := tmpN * (j + 1); // 〃
tmpD := b[j] * b[j + 1]; // 分母
gcd := gcd_BigInteger(tmpN, tmpD); // 最大公約数
a[j] := tmpN div gcd;
b[j] := tmpD div gcd;
end;
if (m > 0) and (m mod 2 = 0) then begin
b0 := b[0];
b0 := b0 * m * (m -1); // m ベルヌーイ数No
NumeratorString[k] := a[0].tostring;
DenominatorString[k] := b0.tostring;
inc(k);
end;
end;
end;
//------------------------------------------------------------------------------
// ログガンマ多倍長
procedure log_GammaMul(var x, ans : mp_float);
var
v, w : mp_float;
tmp, tmp0, s : mp_float;
i : integer;
begin
mpf_init2(v, w);
mpf_init3(tmp, tmp0, s);
mpf_set1(v);
mpf_set_int(tmp, NB);
while mpf_is_lt(x, tmp) do begin
mpf_mul(v, x, v);
mpf_add(x, one, x);
end;
mpf_mul(x, x, tmp); // x^2
mpf_div(one, tmp, w); // w = 1 / x^2
mpf_set0(s);
for i := NB downto 1 do begin
mpf_add(s, BM[i], tmp); // tmp = s + B[i]
mpf_mul(tmp, w, s); // s = tmp * w
end;
mpf_add(s, BM[0], tmp); // tmp = s + B[0]
mpf_div(tmp, x, s); // s = (s + B[0]) / x
mpf_add(s, log_2pis2, s); // s = s + ln(2π)/2
mpf_ln(v, tmp); // ln(v)
mpf_sub(s, tmp, s); // s := s - ln(v)
mpf_sub(s, x, s); // s := s - x
mpf_div(one, two, tmp); // tmp = 1/2
mpf_sub(x, tmp, tmp0); // tmp0 = x - 1/2
mpf_ln(x, tmp); // ln(x)
mpf_mul(tmp0, tmp, tmp0); // tmp0 = (x - 1/2) * ln(x)
mpf_add(s, tmp0, ans); // ans = s + (x - 1/2) * ln(x)
mpf_clear2(v, w);
mpf_clear3(tmp, tmp0, s);
end;
// 多倍長ガンマ
// xの値が 0 と負整数の時Γは∞になるのですが処理をしていませんのでエラーになります。
// ケルビンの次数が整数の時は使用されません。
procedure gammaMul(var x, ans: mp_float);
var
tmp, tmp0, logG : mp_float;
begin
mpf_init3(tmp, tmp0, logG);
if mpf_is_lt(x, zero) then begin
mpf_mul(pai, x, tmp); // x*π
mpf_sin(tmp, tmp0); // sin(πx);
mpf_sub(one, x, tmp); // 1-x
log_GammaMul(tmp, logG); // loggamma(1-x);
mpf_exp(logG, logG); // exp(logG)
mpf_div(pai, tmp0, tmp); // π/sin(πx)
mpf_div(tmp, logG, ans); // ans = π/(sin(πx) * logG(1-x))
end
else begin
log_GammaMul(x, logG); // logG
mpf_exp(logG, ans); // exp(logG)
end;
mpf_clear3(tmp, tmp0, logG);
end;
//------------------------------------------------------------------------------
// 階乗 多倍長
procedure factorialMul(n : integer);
label
EXT;
var
i : integer;
bi, ans : mp_float;
begin
mpf_init2(bi, ans);
mpf_set1(ans);
mpf_copy(ans, FA[0]);
mpf_copy(ans, FA[1]);
mpf_copy(two, bi);
if n <= 1 then begin
goto EXT;
end;
for i := 2 to n do begin
mpf_mul(ans, bi, ans);
mpf_copy(ans, FA[i]);
mpf_add(bi, one, bi);
end;
EXT:
mpf_clear2(bi, ans);
end;
//------------------------------------------------------------------------------
// jv(x) Iv(x) 多倍長
// X 値 実数
// v 次数
// F false Jvx true Ivx
procedure Jvx(var v : mp_float; var x, ri: mp_float; F : boolean);
var
k : integer;
s, x24k, tmp, tmp0, tmp1 : mp_float;
xc, xs2: mp_float;
kd, nd, vk : mp_float;
khg, kf : mp_float;
tmf, tmf0 : mp_float;
sb : mp_float;
begin
mpf_init5(s, x24k, tmp, tmp0, tmp1);
mpf_init2(xc, xs2);
mpf_init2(khg, kf);
mpf_init3(kd, nd, vk);
mpf_init2(tmf, tmf0);
mpf_init(sb);
mpf_set0(s); // Σ=0
mpf_set0(sb);
mpf_div(x, two, xs2); // x / 2
mpf_mul(xs2, xs2, xc); // (x^2)/ 4
mpf_set1(x24k); // x24k = 1
for k := 0 to KMmax do begin
mpf_set1(nd);
mpf_set_int(kf, k); // kf = k
mpf_add(v, kf, tmf0); // k + v
mpf_add(tmf0, one, vk); // vk = k + v + 1;
if mpf_is_lt(vk, zero) then begin // vk < 0 時 nxが整数か確認
mpf_int(vk, tmf); // int(vk);
mpf_sub(vk, tmf, nd); // vk - int(vk) vkが負の整数だったら vk = 0
end;
if mpf_is_ne(vk, zero) and mpf_is_ne(nd, zero) then begin // vkが負の整数の時は計算しない
if mpf_is_ge(v, zero) then
mpf_copy(PVG[k], tmf) // Γ(v+k+1) v>= 0
else
mpf_copy(MVG[k], tmf); // Γ(v+k+1) v < 0
mpf_mul(FA[k], tmf, khg); // k!Γ(n+k+1) vkが0,負の整数の時±∞
mpf_div(x24k, khg, tmp0); // ((i(x^2)/4)^k)/(k!Γ(v+k+1))
if F = false then
if k mod 2 <> 0 then mpf_chs(tmp0, tmp0); // (-1)^k
mpf_add(s, tmp0, s); // Σ
mpf_sub(s, sb, tmp0);
if mpf_is0(tmp0) then break;
mpf_copy(s, sb);
end;
mpf_mul(x24k, xc, x24k); // ((x^2)/4)^k
end;
// x が0で次数vが負数の時power演算ゼロでの除算防止
if mpf_is0(x) and mpf_is_lt(v, zero) then // V<0 x=0 時は無限大になるので計算しない
else begin
mpf_expt(xs2, v, tmp0); // (x/2)^v
mpf_mul(s, tmp0, s); // (x/2)^v * Σ
end;
mpf_copy(s, ri);
mpf_clear5(s, x24k, tmp, tmp0, tmp1);
mpf_clear2(xc, xs2);
mpf_clear2(khg, kf);
mpf_clear3(kd, nd, vk);
mpf_clear2(tmf, tmf0);
mpf_clear(sb);
end;
// zの値が z < 0 の時グラフ用に近似値計算
procedure AiryS_functions(z : mp_float; var Ai, Bi : mp_float);
var
zh3s2, pis4, zh1s4, rpi, tmp : mp_float;
n23zppi4, sincos, az : mp_float;
begin
mpf_init5(zh3s2, pis4, zh1s4, rpi, tmp);
mpf_init3(n23zppi4, sincos, az);
mpf_abs(z, az); // |Z|
mpf_div(one, four, tmp); // 1/4
mpf_expt(az, tmp, zh1s4); // z^(1/4)
mpf_sqrt(pai, rpi); // √π
mpf_div(pai, four, pis4); // π/4
mpf_div(three, two, tmp); // 3/2
mpf_expt(az, tmp, zh3s2); // z^(3/2)
mpf_mul(zh3s2, two, tmp); // 2(z^(3/2))
mpf_div(tmp, three, tmp); // 2/3((z^(3/2)))
mpf_add(tmp, pis4, n23zppi4); // 2/3((z^(3/2))) + π/4
mpf_sin(n23zppi4, sincos); // sin(2/3((z^(3/2))) + π/4)
mpf_div(sincos, rpi, tmp); // sin/√π
mpf_div(tmp, zh1s4, Ai); // sin/√π/z^(1/4)
mpf_cos(n23zppi4, sincos); // cos(2/3((z^(3/2))) + π/4)
mpf_div(sincos, rpi, tmp); // cos/√π
mpf_div(tmp, zh1s4, Bi); // cos/√π/z^(1/4)
mpf_clear5(zh3s2, pis4, zh1s4, rpi, tmp);
mpf_clear3(n23zppi4, sincos, az);
end;
// zの値が z > 0 の時グラフ用に近似値計算
procedure AiryL_functions(z : mp_float; var Ai, Bi : mp_float);
var
zh3s2, zh1s4, ehmzh3s2, tmp : mp_float;
rpi, n2s3z3s2: mp_float;
begin
mpf_init4(zh3s2, zh1s4, ehmzh3s2, tmp);
mpf_init2(rpi, n2s3z3s2);
mpf_div(three, two, tmp); // 3/2
mpf_expt(z, tmp, zh3s2); // z^(3/2)
mpf_mul(zh3s2, two, tmp); // 2z^(3/2)
mpf_div(tmp, three, n2s3z3s2); // (2/3)z^(3/2)
mpf_chs(n2s3z3s2, tmp); // -(2/3)z^(3/2)
mpf_exp(tmp, ehmzh3s2); // e^(-(2/3)z^(3/2))
mpf_div(one, four, tmp); // 1/4
mpf_expt(z, tmp, zh1s4); // z^(1/4)
mpf_sqrt(pai, rpi); // √π
mpf_div(ehmzh3s2, two, tmp); // (e^(-(2/3)z^(3/2)))/2
mpf_div(tmp, rpi, tmp); // (e^(-(2/3)z^(3/2)))/2/√π
mpf_div(tmp, zh1s4, Ai); // Ai = (e^(-(2/3)z^(3/2)))/2/√π/z^(1/4)
mpf_exp(n2s3z3s2, ehmzh3s2); // e^((2/3)z^(3/2))
mpf_div(ehmzh3s2, rpi, tmp); // (e^((2/3)z^(3/2)))/√π
mpf_div(tmp, zh1s4, Bi); // Bi = (e^((2/3)z^(3/2)))/√π/z^(1/4)
mpf_clear4(zh3s2, zh1s4, ehmzh3s2, tmp);
mpf_clear2(rpi, n2s3z3s2);
end;
// Airy関数 多倍長
procedure Airy_functions(z : mp_float; var Ai, Bi : mp_float);
var
pv, mv, az: mp_float;
z32, s23, rz, r3, s32 : mp_float;
sz32, Ipv, Imv, Jpv, Jmv : mp_float;
g23, s16, p323, p316 : mp_float;
begin
mpf_init3(pv, mv, az);
mpf_init5(z32, s23, rz, r3, s32);
mpf_init5(sz32, Ipv, Imv, Jpv, Jmv);
mpf_init4(g23, s16, p323, p316);
mpf_div(one, three, pv); // +v = 1/3
mpf_chs(pv, mv); // -v = -1/3
mpf_div(two, three, s23); // 2/3
mpf_div(pv, two, s16); // 1/6 = 1/3/2
mpf_div(three, two, s32); // 3/2
mpf_abs(z, az); // |z|
if mpf_is0(z) then begin
mpf_expt(three, s23, p323); // 3^(2/3)
gammaMul(s23, g23); // Γ(2/3)
mpf_div(one, p323, Ai); // 1/3^(2/3)
mpf_div(Ai, g23, Ai); // Ai=1/3^(2/3)/Γ(2/3)
mpf_expt(three, s16, p316); // 3^(1/6)
mpf_div(one, p316, Bi); // 1/3^(1/6)
mpf_div(Bi, g23, Bi); // Bi=1/3^(1/6)/Γ(2/3);
end
else begin
mpf_expt(az, s32, z32); // z^(3/2)
mpf_mul(z32, s23, sz32); // (2/3)Z^(3/2)
mpf_sqrt(az, rz); // √z
mpf_sqrt(three, r3); // √3
if mpf_is_ge(z, zero) then begin
Jvx(pv, sz32, Ipv, true); // I+v
Jvx(mv, sz32, Imv, true); // I-v
mpf_sub(Imv, Ipv, Ai); // α=I(-v) - I(+v)
mpf_mul(Ai, rz, Ai); // α√z
mpf_div(Ai, three, Ai); // Ai = (α√z)/3
mpf_add(Imv, Ipv, Bi); // β=I(-v) + I(+v)
mpf_mul(Bi, rz, Bi); // β√z
mpf_div(Bi, r3, Bi); // Bi = (β√z)/√3
// Form1.memo1.Lines.Append( string('I+v = ' + mpf_decimal(Ipv, 50)));
// Form1.memo1.Lines.Append( string('I-v = ' + mpf_decimal(Imv, 50)));
end
else begin
Jvx(pv, sz32, Jpv, false); // J+v
Jvx(mv, sz32, Jmv, false); // J-v
mpf_add(Jmv, Jpv, Ai); // α=J(-v) + J(+v)
mpf_mul(Ai, rz, Ai); // α√z
mpf_div(Ai, three, Ai); // Ai = (α√z)/3
mpf_sub(Jmv, Jpv, Bi); // β=J(-v) - J(+v)
mpf_mul(Bi, rz, Bi); // β√z
mpf_div(Bi, r3, Bi); // Bi=(β√z)/3
// Form1.memo1.Lines.Append( string('J+v = ' + mpf_decimal(Jpv, 50)));
// Form1.memo1.Lines.Append( string('J-v = ' + mpf_decimal(Jmv, 50)));
end;
end;
mpf_clear3(pv, mv, az);
mpf_clear5(z32, s23, rz, r3, s32);
mpf_clear5(sz32, Ipv, Imv, Jpv, Jmv);
mpf_clear4(g23, s16, p323, p316);
end;
// x 入力値限界
// XinMIN <= xin <= XinMAX 範囲外の場合誤差大きくなります。
// 誤差をなくす為には、演算桁数と、Σ値の上限kmax ベルヌーイ数用 NB値を大きく
// する必要が有ります、染ま場合最初の配列の準備の時間が長くなります。
const
XinMIN = -80;
XinMAX = 50;
// 計算
// xの値が大きくなると誤差が大きくなります。
procedure TForm1.Button1Click(Sender: TObject);
label
EXT;
const
N = 100;
XLIN = 5;
CHA = -3;
var
ch, i, NN : integer;
xin : double;
xmin, xmax, dx, xg : double;
xf, xm, Ai, Bi : mp_float;
StopWatch : TStopwatch;
ElapsedMillseconds : Int64;
mm, ss, ms : integer;
begin
memo1.Clear;
memo1.Font.Size := 11;
val(labelededit2.Text, xin, ch);
if ch <> 0 then begin
application.MessageBox('xの値に間違いがあります。','注意', 0);
exit;
end;
if xin < XinMIN then begin
application.MessageBox(PWideChar('xの絶対値は' + intTostr(XinMIN) + 'より大きくして下さい。'),'注意', 0);
exit;
end;
if XinMAX > XinMAX then begin
application.MessageBox(PWideChar('xの絶対値は' + intTostr(XinMAX) + 'より小さくして下さい。'),'注意', 0);
exit;
end;
mpf_init4(xf, xm, Ai, Bi);
series1.Clear;
series2.Clear;
series3.Clear;
series4.Clear;
application.ProcessMessages;
mpf_read_decimal(xm, PAnsiChar(ansistring(labelededit2.Text + #00)));
StopWatch := TStopwatch.StartNew;
Airy_functions(xm, Ai, Bi);
memo1.Lines.Append('エアリー関数');
memo1.Lines.Append( string('Ai(x) = ' + mpf_decimal(Ai, 50)));
memo1.Lines.Append( string('Bi(x) = ' + mpf_decimal(Bi, 50)));
StopWatch.Stop;
ElapsedMillseconds := StopWatch.ElapsedMilliseconds;
ms := ElapsedMillseconds * N + 500;
mm := ms div 60000;
ss := (ms mod 60000) div 1000;
NN := N;
if (xin <= abs(CHA)) and (xin >= CHA) then
memo1.Lines.Append('グラフ表示に約' + inttostr(mm) + '分' + inttostr(ss) + '秒必要です。')
else begin
memo1.Lines.Append('グラフ表示に約2秒必要です。');
NN := N * 2;
end;
if checkbox1.Checked = false then begin // グラフ無だったら終了
Chart1.Canvas.Font.Style := [fsBold];
Chart1.Canvas.Font.size := 8;
Chart1.Canvas.TextOut(170, 115,'グラフ無し');
goto EXT;
end;
// グラフ表示
series3.AddXY(xin, mpf_todouble(Ai));
series4.AddXY(xin, mpf_todouble(Bi));
xmin := round(xin) - 8;
xmax := xmin + 13;
dx := (xmax - xmin) / NN;
for i := 0 to NN do begin
xg := dx * i + xmin;
mpf_set_dbl(xf, xg);
if xg > abs(CHA) then AiryL_functions(xf, Ai, Bi)
else
if xg < CHA then AiryS_functions(xf, Ai, Bi)
else
Airy_functions(xf, Ai, Bi);
series1.AddXY(xg, mpf_todouble(Ai));
series2.AddXY(xg, mpf_todouble(Bi));
end;
application.ProcessMessages;
EXT:
mpf_clear4(xf, xm, Ai, Bi);
end;
// 初期設定
// 計算用配列準備
// ベッセル関数に与える変数の値がz=(2/3)x^(3/2)となり80で約4.8f倍、100とすると約6倍の666となるので
// (z/2)^2k の計算がオーバーフローしないようにする必要があり演算の有効桁数を大きくします。
// 通常の場合z=100で180 Airyの場合x=80で300となります。
// 有効桁数を大きくすると、Γ関数配列の準備に時間が掛かるので、お待ち表示します。
procedure TForm1.Setting;
var
i, k : integer;
N, D, tmp : mp_float;
vm, avm, tmf, tmf0 : mp_float;
nd, vk : mp_float;
begin
mpf_set_default_decprec(300); // 有効桁数300桁 50桁の精度に必要です。
setlength(BM, NB + 1); // ベルヌーイ数配列
setlength(FA, KMmax + 1); // K!配列
setlength(PVG, KMmax + 1); // +vΓ
setlength(MVG, KMmax + 1); // -vΓ
for i := 0 to NB do mpf_init(BM[i]);
for i := 0 to KMmax do mpf_init(FA[i]);
for i := 0 to KMmax do mpf_init(PVG[i]);
for i := 0 to KMmax do mpf_init(MVG[i]);
mpf_init3(N, D, tmp);
mpf_init4(zero, one, two, four);
mpf_init3(three, pai, log_2pis2);
mpf_init4(vm, avm, tmf, tmf0);
mpf_init2(nd, vk);
mpf_set0(zero);
mpf_set1(one);
mpf_set_int(two, 2);
mpf_set_int(three, 3);
mpf_set_int(four, 4);
mpf_set_pi(pai);
mpf_mul(pai, two, tmp); // 2π
mpf_ln(tmp, tmp); // ln(2π)
mpf_div(tmp, two, log_2pis2); // ln(2π)/2
Bernoulli_number_BigInteger; // ベルヌーイ数作成
for i := 0 to NB do begin
mpf_read_decimal(N, PAnsiChar(ansistring(NumeratorString[i] + #00)));
mpf_read_decimal(D, PAnsiChar(ansistring(DenominatorString[i] + #00)));
mpf_div(N, D, BM[i]);
end;
factorialMul(kMmax); // 0!～KMmax!
mpf_div(one, three, vm); // v 1/3
for k := 0 to KMmax do begin
mpf_set_int(tmf, k); // k
mpf_add(tmf, vm, tmf0); // v + k
mpf_add(tmf0, one, vk); // vk= v + k + 1
gammaMul(vk, PVG[k]); // Γ(v+k+1)
end;
mpf_chs(vm, avm); // -v -1/3
for k := 0 to KMmax do begin
mpf_set1(nd);
mpf_set_int(tmf, k); // k
mpf_add(tmf, avm, tmf0); // -v + k
mpf_add(tmf0, one, vk); // vk= -v + k + 1
if mpf_is_lt(vk, zero) then begin // vk < 0 時 nxが整数か確認
mpf_int(vk, tmf); // int(vk);
mpf_sub(vk, tmf, nd); // vk - int(vk) vkが負の整数だったら nd = 0
end;
if mpf_is_ne(vk, zero) and mpf_is_ne(nd, zero) then // vkが負の整数の時は計算しない
gammaMul(vk, MVG[k]) // Γ(v+k+1)
else
mpf_set0(MVG[k]); // Γ(v+k+1) = 0
end;
memo1.Clear;
memo1.Font.Color := clBlack;
memo1.Lines.Append('');
memo1.Lines.Append(' 準備完了');
Labelededit2.EditLabel.Caption := 'x (' + inttostr(XinMIN) + '≦x≦' + inttostr(XinMAX) + ')';
Button1.Enabled := True;
mpf_clear3(N, D, tmp);
mpf_clear4(vm, avm, tmf, tmf0);
mpf_clear2(nd, vk);
end;
// スタート表示
procedure TForm1.FormCreate(Sender: TObject);
begin
Button1.Enabled := False;
memo1.Clear;
memo1.Font.Size := 18;
memo1.Font.Color := clRed;
memo1.Lines.Append('');
memo1.Lines.Append(' 計算用配列準備中');
Timer1.Interval := 200;
Timer1.Enabled := True;
end;
//
procedure TForm1.Timer1Timer(Sender: TObject);
begin
Timer1.Enabled := False;
Setting;
end;
// 終了処理
procedure TForm1.FormClose(Sender: TObject; var Action: TCloseAction);
var
i : integer;
begin
for i := 0 to NB do mpf_clear(BM[i]);
for i := 0 to KMmax do mpf_clear(FA[i]);
for i := 0 to KMmax do mpf_clear(PVG[i]);
for i := 0 to KMmax do mpf_clear(MVG[i]);
mpf_clear4(zero, one, two, four);
mpf_clear3(three, pai, log_2pis2);
end;
end.
ベッセル関数は、級数展開して計算しているので、それを整理したものが、次の様になります。
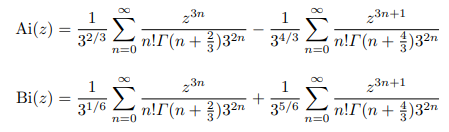
数学・物理通信 ４巻３号 ６巻９号 を参照してください。
"数学・物理通信 ４巻３号" "数学・物理通信 ６巻９号"
をwebで検索すれば見つかります。
zの符号で計算を変える必要はありません。
プログラムリストはエアリー関数部分のみですが、ダウンロードのAiry_function.zipの中には、全てのプログラムが入っています。
n!Γ(n+2/3)3~(2n) と、n!Γ(n+4/3)3^(2n)は配列として先に用意しています。
// Power_series_ Airy関数 多倍長 // z 値 procedure Airy_functions(z : mp_float; var Ai, Bi : mp_float); Label EXT; var n : integer; sz3np, sz3n, z3n, tmp, sz3b: mp_float; zh3, five, six : mp_float; p323, g23, p316 : mp_float; begin mpf_init5(sz3np, sz3n, z3n, tmp, sz3b); mpf_init3(zh3, five, six); mpf_init3(p323, g23, p316); mpf_add(two, four, six); // 6 // z = 0 時のこのルーチンは無くても可 たんに0時の計算を速くする為 if mpf_is0(z) then begin mpf_div(two, three, tmp); mpf_expt(three, tmp, p323); // 3^(2/3) gammaMul(tmp, g23); // Γ(2/3) mpf_div(one, p323, Ai); // 1/3^(2/3) mpf_div(Ai, g23, Ai); // Ai=1/3^(2/3)/Γ(2/3) mpf_div(one, six, tmp); // 1/6 mpf_expt(three, tmp, p316); // 3^(1/6) mpf_div(one, p316, Bi); // 1/3^(1/6) mpf_div(Bi, g23, Bi); // Bi=1/3^(1/6)/Γ(2/3); goto EXT; end; mpf_add(one, four, five); // 5 mpf_mul(z, z, zh3); // z * z mpf_mul(zh3, z, zh3); // z * z * z mpf_set1(z3n); // z^(3n) mpf_set0(sz3n); // Σ=0 mpf_set0(sz3b); for n := 0 to KMmax do begin mpf_div(z3n, MVG[n], tmp); // z^(3n)/(n!Γ(n+2/3)*3^(2n) mpf_add(sz3n, tmp, sz3n); // Σm mpf_sub(sz3n, sz3b, tmp); // Σm- Σback if mpf_is0(tmp) then break; mpf_copy(sz3n, sz3b); mpf_mul(z3n, zh3, z3n); // z^(3n) end; mpf_set1(z3n); // z^(3n) mpf_set0(sz3np); // Σp=0 mpf_set0(sz3b); for n := 0 to KMmax do begin mpf_div(z3n, PVG[n], tmp); // z^(3n)/(n!Γ(n+4/3)*3^(2n) mpf_add(sz3np, tmp, sz3np); // Σp mpf_sub(sz3np, sz3b, tmp); // Σp- Σback if mpf_is0(tmp) then break; mpf_copy(sz3np, sz3b); mpf_mul(z3n, zh3, z3n); // z^(3n) end; mpf_mul(sz3np, z, sz3np); // Σp mpf_div(two, three, tmp); // 2/3 mpf_expt(three, tmp, tmp); // 3^(2/3) mpf_div(sz3n, tmp, Ai); // Σm / (3^(2/3)) mpf_div(four, three, tmp); // 4/3 mpf_expt(three, tmp, tmp); // 3^(4/3) mpf_div(sz3np, tmp, tmp); // Σp / (3^(4/3)) mpf_sub(Ai, tmp, Ai); // Ai mpf_div(one, six, tmp); // 1/6 mpf_expt(three, tmp, tmp); // 3^(1/6) mpf_div(sz3n, tmp, Bi); // Σm / (3^(1/6)) mpf_div(five, six, tmp); // 5/6 mpf_expt(three, tmp, tmp); // 3^(5/6) mpf_div(sz3np, tmp, tmp); // Σp / (3^(5/6)) mpf_add(Bi, tmp, Bi); // Bi EXT: mpf_clear5(sz3np, sz3n, z3n, tmp, sz3b); mpf_clear3(zh3, five, six); mpf_clear3(p323, g23, p316); end;
級数展開 マクローリン展開
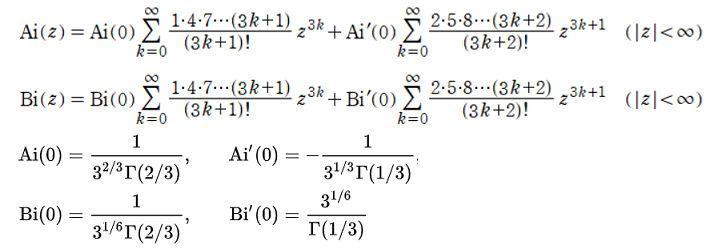
// 多倍長計算 マクローリン展開 procedure Airy_functions(z : mp_float; var Ai, Bi : mp_float); var k, n3kp : integer; s313, g13, s323, g23, s316 : mp_float; Aid, Bid, Ais, Bis , tmp : mp_float; zh3, s0, s1, sd, k3 : mp_float; x3hk, k3p1, k3p2, tmf : mp_float; Ai0, Bi0 : mp_float; begin mpf_init5(s313, g13, s323, g23, s316) ; mpf_init5(Aid, Bid, Ais, Bis, tmp); mpf_init5(zh3, s0, s1, sd, k3); mpf_init5(x3hk, k3p1, tmf, Ai0, Bi0); mpf_init(k3p2); mpf_div(one, three, tmp); // 1/3 mpf_expt(three, tmp, s313); // 3^(1/3) gammaMul(tmp, g13); // Γ(1/3) mpf_div(two, three, tmp); // 2/3 mpf_expt(three, tmp, s323); // 3^(2/3) gammaMul(tmp, g23); // Γ(2/3) mpf_div(one, two, tmp); // 1/2 mpf_div(tmp, three, tmp); // 1/6 mpf_expt(three, tmp, s316); // 3^(1/6); mpf_mul(s323, g23, tmp); // 3^(2/3) * Γ(2/3) mpf_div(one, tmp, Ai0); // Ai0 = 1 / 3^(2/3) / Γ(2/3) mpf_mul(s313, g13, tmp); // 3^(1/3) * Γ(1/3) mpf_div(one, tmp, Aid); // Ai'0 = 1 / 3^(1/3) / Γ(1/3) mpf_chs(Aid, Aid); mpf_mul(s316, g23, tmp); // 3^(1/6) * Γ(2/3) mpf_div(one, tmp, Bi0); // Bi0 = 1 / 3^(1/6) * Γ(2/3) mpf_div(s316, g13, Bid); // Bi'0 = 3^(1/6) / Γ(1/3); mpf_mul(z, z, tmp); // z^2 mpf_mul(tmp, z, zh3); // z^3 mpf_set0(s0); // k = 0 初期値 mpf_set0(sd); // backup mpf_set1(x3hk); // z^(3k) mpf_set1(k3p1); // 3k+1 mpf_set1(k3); // 3k+1 for k := 0 to KMmax do begin mpf_mul_int(three, k, tmp); // 3k mpf_add(tmp, one, k3p1); // 3k + 1 mpf_mul(k3, k3p1, k3); // 1.4.7..(3k+1) n3kp := (3 * k + 1); // 3k + 1 mpf_div(k3, FA[n3kp], tmp); // 1.4.7..(3k+1)/(3k+1)! mpf_mul(tmp, x3hk, tmf); // 1.4.7..(3k+1)/(3k+1)! * Z^(3k) mpf_add(s0, tmf, s0); // Σ if mpf_is_eq(s0, sd) then break; mpf_copy(s0, sd); mpf_mul(x3hk, zh3, x3hk); // (z^(3^k) end; mpf_set0(s1); // k=0 初期値 mpf_set0(sd); // backup mpf_set1(x3hk); // z^(3k) mpf_set1(k3p2); // 1 mpf_set1(k3); // 1 for k := 0 to KMmax do begin mpf_mul_int(three, k, tmp); // 3k mpf_add(tmp, two, k3P2); // 3k + 2 mpf_mul(k3, k3p2, k3); // 2.5.8..(3k+2) n3kp := (3 * k + 2); // 3k + 2 mpf_div(k3, FA[n3kp], tmp); // 2.5.8..(3k+2)/(3k+2)! mpf_mul(tmp, x3hk, tmf); // 2.5.8..(3k+2)/(3k+2)! * z^(3k) mpf_add(s1, tmf, s1); // Σ if mpf_is_eq(s1, sd) then break; mpf_copy(s1, sd); mpf_mul(x3hk, zh3, x3hk); // (z^(3^k) end; mpf_mul(s1, z, s1); // z^(3k+1) mpf_mul(s0, Ai0, Ais); // Ais = Σ0 * Ai(0) mpf_mul(s1, Aid, tmf); // Σ1 * Ai'(0) mpf_add(tmf, Ais, Ai); // Ai mpf_mul(s0, Bi0, Bis); // Bis = Σ0 * Bi(0) mpf_mul(s1, bid, tmp); // Σ1 * Bi'(0) mpf_add(tmp, Bis, Bi); // Bi mpf_clear5(s313, g13, s323, g23, s316) ; mpf_clear5(Aid, Bid, Ais, Bis, tmp); mpf_clear5(zh3, s0, s1, sd, k3); mpf_clear5(x3hk, k3p1, tmf, Ai0, Bi0); mpf_clear(k3p2); end;
前記マクローリン展開は分かりずらいので、次の展開式を検討
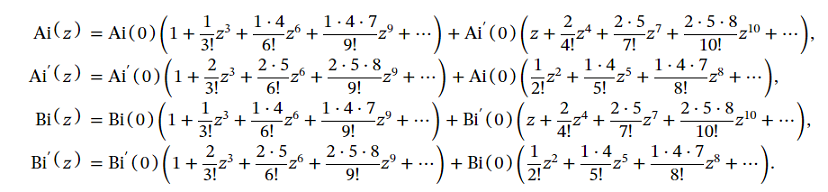
一次微分に関しては今回は省略
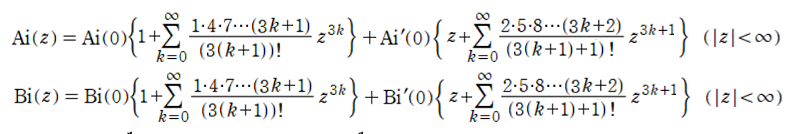
Γ関数の使用をやめる為、Ai(0), Bi(0), Ai'(0), Bi'(0)は、定数として与えます。
計算結果の有効桁数は50桁ですが、140桁程度必要です、計算範囲はZ=-75～25程度です。
指定値のエアリー関数については、BigDecimalで計算します。
BigDecimalの演算には、除算以外の計算には、桁数制限が無く桁数が大きくなりすぎて、演算出来なくなる場合があるので、適宜必要な桁数で丸め処理を行う必要があります。
此処の計算では、250桁に設定しています。
50桁の答えを表示する場合は、テキストで出力する直前で、50桁に丸めます。
const PRE = 250; // Bigdecimal 有効桁数 // 多倍長計算 BigDecimal マクローリン展開 procedure Airy_functions(x : Bigdecimal; var Ai, Bi : Bigdecimal); const Ai0S = '3.55028053887817239260063186004183176397979174199177240583326510300810042450126712957174246054040271688420448730349495839758292670446161937E-1'; AidS ='-2.58819403792806798405183560189203963479091138354934582210001813856102772676790280654196405827275384313371193211789133381275035952167626014E-1'; Bi0S = '6.14926627446000735150922369093613553594728188648596505040878753014296519305520640529387343345267569240728438782242516724523554227287639109E-1'; BidS = '4.48288357353826357914823710398828390866226799212262061082808778372330755009780647185046574400736362878496329249031699773802889479552819613E-1'; var k : integer; s0, s1, sb: Bigdecimal; s3kp1, s3kp2, k3p11h, k3p1h, k3p11 : Bigdecimal; k3p1, k3p2, kk3p1 : bigdecimal; xh3, sxh3, tmp : Bigdecimal; ai0, aid, bi0, bid : Bigdecimal; begin s0 := '0'; // 初期値 0 sb := '0'; // 0 xh3 := x * x * x; // x^3 sxh3 := '1'; // 1 x^(3k) s3kp1 := '1'; // 1 * 3(k+1) k3p1h := '1'; // 1 (3(k+1))! for k := 0 to KMmax do begin sxh3 := sxh3 * xh3; // x^(3k) sxh3 := sxh3.RoundToPrecision(PRE); k3P1 := 3 * k + 1; // 3k+1 s3kp1 := s3kp1 * k3P1; // 1.4.7.(3k + 1); s3kp1 := s3kp1.RoundToPrecision(PRE); kk3p1 := 3 * (k + 1); // 3*(k+1); k3p1h := k3p1h * (kk3p1 - 2) * (kk3p1 - 1) * (kk3p1); // (3*(k+1))! k3p1h := k3p1h.RoundToPrecision(PRE); tmp := s3kp1 * sxh3 / k3p1h; // 1.4.7.(3k + 1) * x^(3k) / (3*(k+1))! s0 := s0 + tmp; // Σ s0 := s0.RoundToPrecision(PRE); if s0 = sb then break; sb := s0; end; s0 := s0 + 1; // 1 + Σ s1 := 0; // 初期値 0 sb := 0; // x^3k sxh3 := '1'; // x^(3k) s3kp2 := '1'; // 1 *(3k+2) k3p11h := '1'; // 1 (3*(k+1)+1)! for k := 0 to KMmax do begin sxh3 := sxh3 * xh3; // x^(3k) sxh3 := sxh3.RoundToPrecision(PRE); k3P2 := 3 * k + 2; // 3k+2 s3kp2 := s3kp2 * k3P2; // 2.5.8.(3k+2) s3kp2 := s3kp2.RoundToPrecision(PRE); k3p11 := 3 * (k + 1) + 1; // 3*(k+1)+1 k3p11h := k3p11h * (k3p11 - 2) * (k3p11 - 1) * (k3p11); // (3*(k+1)+1)! k3p11h := k3p11h.RoundToPrecision(PRE); tmp := s3kp2 * sxh3 / k3p11h; // 2.5.8.(3k+2) * x^(3k) / ((3*(k+1)+1)!) s1 := s1 + tmp; // Σ s1 := s1.RoundToPrecision(PRE); if s1 = sb then break; sb := s1; end; s1 := s1 * x + x; // x + xΣ ai0 := Ai0S; aid := AidS; bi0 := Bi0S; bid := BidS; Ai := s0 * ai0; Ai := Ai + s1 * aid; Bi := s0 * bi0; Bi := Bi + s1 * bid; end;
マクローリン展開を更に整理をすると次の様な簡単な、展開式になります。
計算速度は、Airy functionの中で一番速く計算できます。
const PRE = 250; // Bigdecimal 有効桁数 // 多倍長計算 BigDecimal マクローリン展開 procedure Airy_functions(x : Bigdecimal; var Ai, Bi : Bigdecimal); const Ai0S = '3.55028053887817239260063186004183176397979174199177240583326510300810042450126712957174246054040271688420448730349495839758292670446161937E-1'; AidS ='-2.58819403792806798405183560189203963479091138354934582210001813856102772676790280654196405827275384313371193211789133381275035952167626014E-1'; Bi0S = '6.14926627446000735150922369093613553594728188648596505040878753014296519305520640529387343345267569240728438782242516724523554227287639109E-1'; BidS = '4.48288357353826357914823710398828390866226799212262061082808778372330755009780647185046574400736362878496329249031699773802889479552819613E-1'; var n : integer; s0, s1, sb: Bigdecimal; s23, s34 : Bigdecimal; xh3, sxh3, tmp : Bigdecimal; ai0, aid, bi0, bid : Bigdecimal; begin s0 := 0; // 0 sb := 0; // 0 xh3 := x * x * x; // x^3 sxh3 := xh3; s23 := 1; // 1 for n := 1 to KMmax do begin s23 := s23 * (3 * n - 1) * (3 * n); // (2,3),(5,6),,,((3n-1) * 3n) s23 := s23.RoundToPrecision(PRE); // 桁数制限 tmp := sxh3 / s23; // 除算は規定で桁数制限有り s0 := s0 + tmp; // s0 := s0 + (x^3)/((2,3),(5,6),,,)((3n-1) * 3n)) s0 := s0.RoundToPrecision(PRE); // 桁数制限 if s0 = sb then break; // Σ値が変化しなくなったら終了 sxh3 := sxh3 * xh3; // x^6 9 12 sxh3 := sxh3.RoundToPrecision(PRE); // 桁数制限 sb := s0; end; s0 := s0 + 1; s1 := 0; sb := 0; sxh3 := xh3; // x^3 s34 := 1; for n := 1 to KMmax do begin s34 := s34 * (3 * n) * (3 * n + 1); // (3,4),(6,7),,,(3n * (3n+1)) s34 := s34.RoundToPrecision(PRE); // 桁数制限 tmp := sxh3 / s34; // 除算は規定で桁数制限有り s1 := s1 + tmp; // s1 := s1 + (x^3n)/((3,4),(6,7),,,(3n * (3n+1))) s1 := s1.RoundToPrecision(PRE); // 桁数制限 if s1 = sb then break; // Σ値が変化しなくなったら終了 sxh3 := sxh3 * xh3; // x^6 9 12 sxh3 := sxh3.RoundToPrecision(PRE); // 桁数制限 sb := s1; end; s1 := s1 * x + x; // x + xΣ x + Σ(x^(3n+1)/(3n * (3n+1))) ai0 := Ai0S; aid := AidS; bi0 := Bi0S; bid := BidS; Ai := s0 * ai0; Ai := Ai + s1 * aid; Bi := s0 * bi0; Bi := Bi + s1 * bid; end;
一般 Airy 関数
一般 Airy関数の詳細については特殊関数 グラフィックスライブラリーを参照して下さい。
通常のAiry関数の次数ベッセル関数の次数V=1/3として計算していますが、一般 Airy関数では、次数V=1が通常のAiry
関数と同じになるようにして計算しています。
次数がV=-1だと無限大なるので、次数Vは-1より大きい値となります。
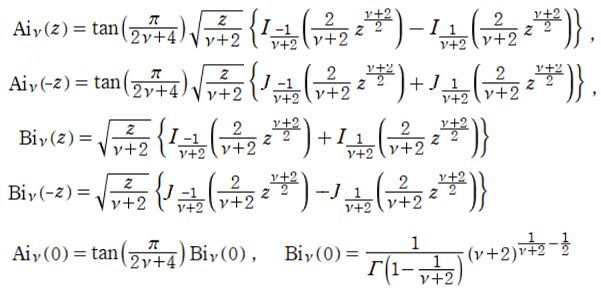
次数vの値が-1だと、tanの値が無限大となります。
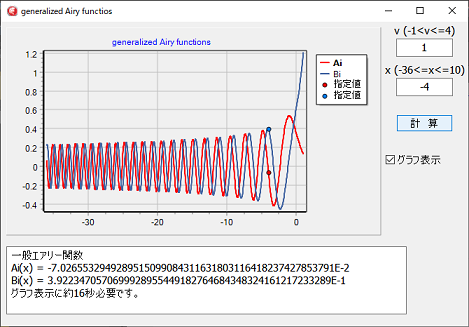
vの値が大きくなると、計算に大きな桁数が必要となるので、ここのプログラムでは、次数の最大値をv=4にしています。
漸近計算が出来ないため、グラフの計算に時間が掛かるので、次数vの値が変更されない限り、グラフの曲線は再計算せず、指定値のみ計算します。
プログラム
// generalized Airy関数 多倍長 // pv. mv J, I 用次数 // tanpis2 tan(π/(2v+4)) // v generalized Airyの次数 v=1 が Airyの(1/3)vに相当 // z 値 procedure generalized_Airy_functions(pv, mv, tanpis2, v, z : mp_float; var Ai, Bi : mp_float); label EXT; var az: mp_float; vp2, s2vp2, vp2s2 : mp_float; bi0, ai0 : mp_float; harf, invvp2, tmp, tmf : mp_float; sqrtzsvp2, zij: mp_float; IJmv, IJpv : mp_float; begin mpf_init(az); mpf_init3(vp2, s2vp2, vp2s2); mpf_init2(bi0, ai0); mpf_init4(harf, invvp2, tmp, tmf); mpf_init2(sqrtzsvp2, zij); mpf_init2(IJmv, IJpv); mpf_add(v, two, vp2); // v + 2 if mpf_is0(z) then begin mpf_div(one, two, harf); // 1/2 mpf_inv(vp2, invvp2); // 1/(v+2) mpf_sub(invvp2, harf, tmp); // 1/(v+2)-1/2 mpf_expt(vp2, tmp, tmp); // (v+2)^(1/(v+2)-1/2) mpf_sub(one, invvp2, tmf); // 1-1/(v+2) gammaMul(tmf, tmf); // Γ(1-1/(v+2)); mpf_div(tmp, tmf, bi); // bi0 = ((v+2)^(1/(v+2)-1/2))/Γ(1-1/(v+2)) mpf_mul(tanpis2, bi, ai); // ai0 = tan(π/(2v+4)) * Bi0 goto EXT; end; mpf_abs(z, az); mpf_div(az, vp2, tmp); // z/(v+2) mpf_sqrt(tmp, sqrtzsvp2); // √z/(v+2) mpf_div(two, vp2, s2vp2); // 2/(v+2); mpf_div(vp2, two, vp2s2); // (v+2)/2 mpf_expt(az, vp2s2, tmf); // z^((v+2)/2) mpf_mul(tmf, s2vp2, zij); // zij = 2/(v+2) * z^((v+2)/2) if mpf_is_gt(z, zero) then begin Jvx(mv, zij, IJmv, true); // I-v Jvx(pv, zij, IJpv, true); // I+v mpf_sub(IJmv, IJpv, tmf); // I-v - I+v mpf_mul(tmf, sqrtzsvp2, tmp); // (I-v - I+v) * √(z/(v+2) mpf_mul(tmp, tanpis2, Ai); // Ai = (I-v - I+v) * √(z/(v+2) * tan(π/(2v+4)) mpf_add(IJmv, IJpv, tmf); // I-v + I+v mpf_mul(tmf, sqrtzsvp2, Bi); // Bi := (I-v + I+v) * √(z/(v+2) end; if mpf_is_lt(z, zero) then begin Jvx(mv, zij, IJmv, false); // J-v Jvx(pv, zij, IJpv, false); // J+v mpf_add(IJmv, IJpv, tmf); // J-v + J+v mpf_mul(tmf, sqrtzsvp2, tmp); // (J-v + J+v) * √(z/(v+2) mpf_mul(tmp, tanpis2, Ai); // Ai = (J-v + I+v) * √(z/(v+2) * tan(π/(2v+4)) mpf_sub(IJmv, IJpv, tmf); // J-v - J+v mpf_mul(tmf, sqrtzsvp2, Bi); // Bi := (J-v - J+v) * √(z/(v+2) end; EXT: mpf_clear(az); mpf_clear3(vp2, s2vp2, vp2s2); mpf_clear2(bi0, ai0); mpf_clear4(harf, invvp2, tmp, tmf); mpf_clear2(sqrtzsvp2, zij); mpf_clear2(IJmv, IJpv); end;
Airy_function.zip
三角関数、逆三角関数、その他関数 に戻る