第２種球ベッセル関数

ベッセル関数の詳細については、Webで検索して参照してください。

　左図は第２種の球ベッセル関数の計算式ですが、第２種ベッセル関数の実数計算により簡単に求めることが出来ます。
第２種ベッセル関数の計算については、第２種ベッセル関数を参照すれば分かります。

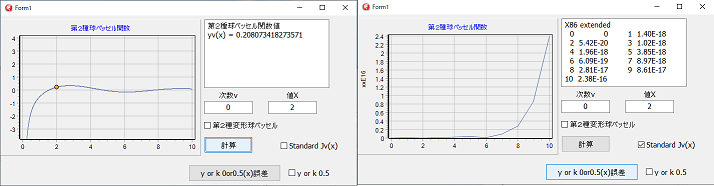
　次の図は、プログラムの実行画面です。
Xの値が大きくなると、計算の有効桁数の関係で、誤差が大きくなるのは第２種ベッセル関数と変わりません。
あまり大きな値を与えると、誤差の方が大きくなります。

　プログラムは、第２種ベッセル関数から、第２種球ベッセルに変更するにあたって、計算精度向上の為、ガンマ関数、ディガンマ関数の計算方法を変更してあります。
ガンマ関数は、対数計算、ディガンマ関数は、ゼロ以上の整数計算にしました。
第２種ベッセル関数も変更すれは、計算精度が向上します。

プログラム

// Xの値　積分計算の上限値MNによってオーバーフローを発生するので
// コンパイル設定にオーバーフローチックが必須です。
// 第二種ベッセル関数の場合次数vが整数の時と、非整数の時で、別の計算をします。
// Xの値が大きくなると誤差が大きくなります 演算有効桁数不足
unit Main;

interface

uses
  Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
  Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.ExtCtrls, Vcl.StdCtrls, Vcl.Buttons, system.Math,
  system.UITypes, VclTee.TeeGDIPlus, VCLTee.TeEngine, VCLTee.Series,
  VCLTee.TeeProcs, VCLTee.Chart;

type
  TForm1 = class(TForm)
    BitBtn1: TBitBtn;
    Memo1: TMemo;
    LabeledEdit1: TLabeledEdit;
    Chart1: TChart;
    Series1: TLineSeries;
    CheckBox1: TCheckBox;
    LabeledEdit2: TLabeledEdit;
    Series2: TPointSeries;
    Button1: TButton;
    CheckBox3: TCheckBox;
    CheckBox2: TCheckBox;
    procedure BitBtn1Click(Sender: TObject);
    procedure Button1Click(Sender: TObject);
  private
    { Private 宣言 }
  public
    { Public 宣言 }
    procedure GraphNnX(xmax, v: extended);
    procedure GraphKnX(xmax, v:extended);
  end;

var
  Form1: TForm1;

implementation

{$R *.dfm}

const

// 誤差計算用データー
  k05x: array[0..10] of extended = (infinity,
                                  0.4802524860099896844602,
                                  0.07891087361460348685438,
                                  0.01849841602458628046582,
                                  0.004980195513475615411195,
                                  0.001443218477709391358495,
                                  4.377616999209552134537E-4,
                                  1.369687289039624644564E-4,
                                  4.382884545220336481172E-5,
                                  1.426538241889837020678E-5,
                                  4.70533267971335579845E-6
                                 );

  k0x: array[0..10] of extended = (infinity,
                                  0.3678794411714423215955,
                                  0.067667641618306345947,
                                  0.01659568945595464765978,
                                  0.00457890972218354507343,
                                  0.001347589399817093419327,
                                  4.131253627777264038409E-4,
                                  1.302688522220737440005E-4,
                                  4.193282848781397985267E-5,
                                  1.371220045407550549974E-5,
                                  4.539992976248485153559E-6
                                 );

  y05x: array[0..10] of extended = (-infinity,
                                  -0.979105073187779411997,
                                  -0.0948550227282578848964,
                                   0.2349348211023303844977,
                                   0.2493629593212646219752,
                                   0.0828771619936813904809,
                                  -0.08954637974475401842893,
                                  -0.1433759573238180132626,
                                  -0.07003871851786339196898,
                                   0.04357964394070161754787,
                                   0.09869296282843609949355
                                 );

  y0x: array[0..10] of extended = (infinity,
                                 -0.5403023058681397174009,
                                  0.2080734182735711934988,
                                  0.3299974988668151524239,
                                  0.1634109052159029786598,
                                 -0.05673243709264525289333,
                                 -0.1600283811083943367576,
                                 -0.1077003220490435197345,
                                  0.01818750422607669073361,
                                  0.1012366957649641098187,
                                  0.08390715290764524522589
                                );


//ベルヌーイ数B(2)、B(4)、B(6)、...、B(20)

  B : array[1..10] of extended = ( 1.0 / 6,           // B(2)
                                  -1.0 / 30,
                                   1.0 / 42,
                                  -1.0 / 30,
                                   5.0 / 66,
                                -691.0 / 2730,
                                   7.0 / 6,
                               -3617.0 / 510,
                               43867.0 / 798,
                             -174611.0 / 330);        //  B(20)

  m: integer = sizeof(B) div sizeof(extended);

//------------------------------------------------------------------------------
// 対数ガンマ関数
function Log_Gamma(x: extended): extended;
var
  i : integer;
  sum : extended;
  xx, v  : extended;
  ln_sqrt_2pi: extended;
begin
  ln_sqrt_2pi := ln(sqrt(2 * pi));                    // = ln(2 * pi) / 2;
  sum := 0;
  v := 1;
　while x < m do begin
    v := v * x;
    x := x + 1;
  end;
  xx := 1 / (x * x);
  for i := m downto  2 do
    sum := (sum + B[i] / (i * 2 * (2 * i - 1))) * xx;
  result := (sum + B[1] / 2) / x
      + ln_sqrt_2pi - ln(v) - x + (x - 0.5) * ln(x);
end;

// ガンマ関数
function Gamma_Function(x: extended): extended;
begin
  if x < 0 then begin
    result := pi / (sin(pi * x) * exp(log_Gamma(1 - x)));
  end
  else begin
    result := exp(Log_Gamma(x));
  end;
end;

//------------------------------------------------------------------------------
// ディガンマ関数 整数n >= 0
function Digamma_Function(n: integer): extended;
const
  g= 0.5772156649015328606065120;
var
  s : extended;
  k : integer;
begin
  if n = 0 then begin
    result := -infinity;
    exit;
  end;
  if n = 1 then begin
    result := -g;
    exit;
  end;
  s := 0;
  for k := 1 to n - 1 do s := s + 1 / k;
  result := s - g;
end;

//----------------------- new --------------------------------------------------
// X 値
// v 次数
// flag false 通常 true 変形
function Jvx(v, x: double; flag: boolean): extended;
var
  k : integer;
  g, j, bkk: extended;

  function Bk(k : integer): extended;
  var
    kn : integer;
    Bn, Y, Zk: extended;
  begin
    Y := -(x / 2) * (x / 2);
    if flag then Y := -Y;
    Bn := 1;
    for kn := 1 to k do begin
      Zk := Y / (kn * (kn + v));
      Bn := Zk * Bn;
    end;
    result := Bn
  end;

begin
  g := Gamma_Function(1 + v);
  bkk := 0;
  for k := 0 to 100 do  bkk := bkk + Bk(k);
  j := power(x / 2, v) / g * bkk;
  result := j;
end;

// 第１種ベッセル関数 Γ関数使用
// X 値
// v 次数
// flag false 通常 true 変形
function BesselG(X: extended; v: extended;  flag: boolean): extended;
const
  MN = 100;
var
  M : Integer;
  B, S  : extended;
begin
  S := 0;
  for M := 0 to MN do begin
    B := 1 / Gamma_Function(M + 1) / Gamma_Function(M + v + 1);   // B = 1 / (Γ(m + 1)Γ(m + n + 1))
    if not flag then
      S := S + power(-1, M) * B * power(X / 2, 2 * M + v)
    else
      S := S + B * power(X / 2, 2 * M + v)
  end;
  result := S;
end;

// 第２種ベッセル関数
// 次数v   非整数
// 値 x
function Yax(v, x: extended): extended;
begin
  if Form1.CheckBox2.Checked = true then
    result := (BesselG(x, v, false) * cos(v * pi) - BesselG(x, -v, false)) / sin(v * pi)
  else
    result := (Jvx(v, x, false) * cos(v * pi) - Jvx(-v, x, false)) / sin(v * pi);
end;

// 第２種ベッセル関数
// X　値
// n 次数 整数
// Mの値は積分上は∞となっていますが精度上50程度で問題ないようです。
function Ynx(x: extended; n: integer): extended;
const
  {$IFDEF CPUX64}
  M = 50;
  {$ELSE}
  M = 100;                                  // 値を大きくするとオーバーフローします。
  {$ENDIF}
var
  k : integer;
  a, b, c: extended;
begin
  if Form1.checkbox2.Checked = true then
    a := 2 / pi * ln(x / 2) * BesselG(x, n, False)
  else
    a := 2 / pi * ln(x / 2) * Jvx(n, x, False);
  b := 0;
  for k := 0 to n - 1 do
    b := b + (Gamma_Function(n - k) / Gamma_Function(k + 1)) * power(x / 2, 2 * k - n);
  b := b / pi;
  c := 0;
  for k := 0 to M do
    c := c + power(-1, k) * (Digamma_Function(K + 1) + Digamma_Function(k + n + 1))
                         * power(x / 2, 2 * k + n) / (Gamma_Function(k + 1) * Gamma_Function(n + k + 1));
  c := c / pi;
  result := (a - b - c);
end;

// 第２種変形ベッセル関数
// 次数v   非整数
// 値 x
function Kax(v, x: extended): extended;
begin
  if Form1.checkbox2.Checked = true then
    result := pi / 2 * ((BesselG(x, -v, true) - BesselG(x, v, true)) / sin(v * pi))
  else
    result := pi / 2 * ((Jvx(-v, x, true) - Jvx(v, x, true)) / sin(v * pi));
end;

// 第２種変形ベッセル関数
// X　値
// n 次数 整数
// Mnの値は積分上は∞となっていますが精度上50程度で問題ないようです。
function KnX(x: extended; n: integer): extended;
const
  {$IFDEF CPUX64}
  MN = 50;
  {$ELSE}
  MN = 100;                                  // 値を大きくするとオーバーフローします。
  {$ENDIF}
var
  a, b, c: extended;
  p : integer;
begin
  if Form1.CheckBox2.Checked = True then
    a := power(-1, n + 1) * BesselG(x, n, true) * ln(x / 2)
  else
    a := power(-1, n + 1) * Jvx(n, x, true) * ln(x / 2);
  b := 0;
  for p := 0 to Mn do
    b := b + 1 / Gamma_Function(p + 1) / Gamma_Function(n + p + 1) * power(x / 2, 2 * p)
    * (Digamma_Function(p + 1) + Digamma_Function(p + n + 1));
  b := b * power(- 1, n) / 2 * power(x / 2, n);
  c := 0;
  for p := 0 to n - 1 do
    c := c + power(-1, p) * Gamma_Function(n - p) / Gamma_Function(p + 1) * power(x / 2, 2 * p);
  c := c / 2 * power(x / 2, -n);
  result := a + b + c;
end;

// 第２種ベッセル関数
// v 次数
// x 値
function Yvx(v, x: extended): extended;
var
  n: integer;
begin
  n := round(v);
  if n = v then begin
    if n < 0 then n := abs(n);
    result := Ynx(x, n);
    if v < 0 then result := result * power(-1, n);
  end
  else result := Yax(v, x);
end;

// 第２種球ベッセル関数グラフ表示
// xmax Xの最大値
// n 次数
procedure TForm1.GraphNnX(xmax, v: extended);
const
  NMAX = 1000;
var
  Y, X: extended;
  I  : integer;
  XMIN: extended;
begin
  XMIN := 0.001;
  for I := 0 to NMAX - 1 do begin
    X := XMIN + (xmax - XMIN) * I / NMAX;
    Y := sqrt(pi / (2 * x)) * Yvx(v + 0.5, X);
    if Y > 10000 then Y := 10000;
    if Y < -10000 then Y := -10000;
    Series1.AddXY(X, Y);
  end;
end;

// 第２種変形ベッセル関数
// v 次数
// x 値
function kvx(v, x: extended): extended;
var
  n: integer;
begin
  n := round(v);
  if n = v then begin
    if n < 0 then n := abs(n);
    result := KnX(x, n);
  end
  else result := KaX(v, x);
end;

// 第２種変形球ベッセル関数グラフ表示
// xmax Xの最大値
// n 次数
procedure TForm1.GraphKnX(xmax, v: extended);
const
  NMAX = 1000;
var
  Y, X: extended;
  I: integer;
  XMIN: extended;
begin
  XMIN := 0.001;
  for I := 1 to NMAX - 1 do begin
    X := XMIN + (xmax - XMIN) * I / NMAX;
    Y := sqrt(2 / (pi * x)) * Kvx(v + 0.5, x);
    if Y > 10000 then Y := 10000;
    if Y < -10000 then Y := -10000;
    Series1.AddXY(X, Y);
  end;
end;

// 第２種球ベッセル関数計算
procedure TForm1.BitBtn1Click(Sender: TObject);
var
  x, v, y: extended;
  ch: integer;
begin
  val(Labelededit2.Text, v, ch);
  if ch <> 0 then begin
    MessageDlg('次数xに間違いがあります。', mtInformation, [mbOk], 0, mbOk);
    exit;
  end;
  val(Labelededit1.Text, x, ch);
  if ch <> 0 then begin
    MessageDlg('値xに間違いがあります。', mtInformation, [mbOk], 0, mbOk);
    exit;
  end;
  if x < 0 then begin
    MessageDlg('値xは0(ゼロ)以上にして下さい。', mtInformation, [mbOk], 0, mbOk);
    exit;
  end;
  if x > 30 then begin
    MessageDlg('値xが大きすぎます。', mtInformation, [mbOk], 0, mbOk);
    exit;
  end;
  Series1.Clear;
  Series2.Clear;
  memo1.Clear;
  y := 0;
  Chart1.Title.Text.Clear;
  chart1.LeftAxis.Title.Caption := '';
  if checkbox1.Checked = false then begin
    Chart1.Title.Text.Append('第２種球ベッセル関数');
    if x > 0 then begin
      y := sqrt(pi / (2 * x)) * Yvx(v + 0.5, X);
      if Chart1.LeftAxis.Minimum >= y + 4 then begin
        Chart1.LeftAxis.Minimum := y - 4;
        Chart1.LeftAxis.Maximum := y + 4;
      end
      else begin
        Chart1.LeftAxis.Maximum := y + 4;
        Chart1.LeftAxis.Minimum := y - 4;
      end;
      GraphNnX(10, v);
      memo1.Lines.Add('第２種球ベッセル関数値');
      memo1.Lines.Add('yv(x) = ' + floatTostr(y));
    end;
  end
  else begin
    Chart1.Title.Text.Append('第２種変形球ベッセル関数');
    if x > 0 then begin
      y := sqrt(2 / (pi * x)) * Kvx(v + 0.5, x);
      if Chart1.LeftAxis.Minimum >= y + 4 then begin
        Chart1.LeftAxis.Minimum := y - 1;
        Chart1.LeftAxis.Maximum := Y + 4;
      end
      else begin
        Chart1.LeftAxis.Maximum := Y + 4;
        Chart1.LeftAxis.Minimum := y - 1;
      end;
      GraphKnX(10, v);
      memo1.Lines.Add('第２種変形球ベッセル関数値');
      memo1.Lines.Add('kv(x) = ' + floatTostr(y));
    end;
  end;
  if (x > 0) and (abs(y) < 9996) then Series2.AddXY(x, y);
  if x = 0 then begin
    if checkbox1.Checked = false then begin
      memo1.Lines.Add('第２種球ベッセル関数値');
      if v > 0 then
        memo1.Lines.Add('yv(x) = - ∞')
      else
        memo1.Lines.Add('yv(x) = ∞');
    end
    else begin
      memo1.Lines.Add('第２種変形球ベッセル関数値');
      memo1.Lines.Add('kv(x) = ∞');
    end;
  end;
end;

// 計算誤差の確認
procedure TForm1.Button1Click(Sender: TObject);
var
  i, p, l: integer;
  yk: extended;
  def : extended;
  defs, re, ex, ads, no : string;
begin
  memo1.Clear;
  Series1.Clear;
  Series2.Clear;
  chart1.LeftAxis.AutomaticMaximum := true;
  chart1.LeftAxis.Minimum := 0;
  {$IFDEF CPUX64}
  chart1.LeftAxis.Title.Caption := 'xxE16';
  Memo1.Lines.Append('X64 double');
  {$ELSE}
  chart1.LeftAxis.Title.Caption := 'xxE16';
  Memo1.Lines.Append('X86 extended');
  {$ENDIF}
  for i := 0 to 10 do begin
    if i <> 0 then begin
      if checkbox3.Checked = true then begin
        if checkbox1.Checked = false then begin
          yk := sqrt(pi / (2 * i)) * Yvx(1, i);
          def := abs(Y05x[i] - yk);
        end
        else begin
          yk := sqrt(2 / (pi * i)) * kvx(1, i);
          def := abs(k05x[i] - yk);
        end;
      end
      else begin
        if checkbox1.Checked = false then begin
          yk := sqrt(pi / (2 * i)) * Yvx(0.5, i);
          def := abs(Y0x[i] - yk);
        end
        else begin
          yk := sqrt(2 / (pi * i)) * kvx(0.5, i);
          def := abs(k0x[i] - yk);
        end;
      end;
    end
    else def := 0;
    {$IFDEF CPUX64}
    Series1.AddXY(i, def * 1E16);
    {$ELSE}
    Series1.AddXY(i, def * 1E16);
    {$ENDIF}
    if def <> 0 then
      defs := floatTostr(def)
    else defs := '      0';

    l := length(defs);
    p := pos('E', defs, 1);
    re := copy(defs, 0, 4);
    ex := copy(defs, p, l - p + 1);
    no := inttostr(i);
    if i < 10 then no := '  ' + no;
    if i mod 2 = 0 then  begin
      ads := no + '  ' + re + ex;
      if i = 10 then memo1.Lines.Text := memo1.Lines.Text + ads;
    end
    else begin
      ads := ads + '      ' + no + '  ' + re + ex;
      memo1.Lines.Append(ads);
    end;
  end;
end;

end.

　　　Spherical_Bessel2a_function.zip

各種プログラム計算例に戻る