
誤差関数erf の 1 - Γ(1/2, z2)/√π は γ(1/2,z2)/√π と同じです。
ガウシアン分布
ガウシアン分布(ガウス分布)は正規分布で、確率論や統計学で用いられています。
平均 μ = 0, σ2 = 1 の時は標準正規分布と呼ばれています。
詳細についてはウィキペディア(Wikipedia)を見て下さい。

誤差関数erf の 1 - Γ(1/2, z2)/√π は γ(1/2,z2)/√π と同じです。
標準正規分布については、不完全ガンマ関数の応用にもありますので参照してください。
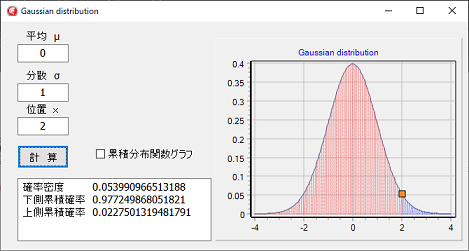
分散はσ2ではなく σ なので注意してください
プログラム
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.Buttons, Vcl.ExtCtrls, VclTee.TeeGDIPlus,
VCLTee.Series, VCLTee.TeEngine, VCLTee.TeeProcs, VCLTee.Chart;
type
TForm1 = class(TForm)
Memo1: TMemo;
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
LabeledEdit3: TLabeledEdit;
BitBtn1: TBitBtn;
Chart1: TChart;
Series1: TLineSeries;
Series2: TPointSeries;
Series3: TLineSeries;
CheckBox1: TCheckBox;
procedure BitBtn1Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
const
//ベルヌーイ数B(2)、B(4)、B(6)、...、B(16)
B : array[1..8] of double = ( 1.0 / 6, // B(2)
-1.0 / 30,
1.0 / 42,
-1.0 / 30,
5.0 / 66,
-691.0 / 2730,
7.0 / 6,
-3617.0 / 510); // B(16)
m: integer = sizeof(B) div sizeof(double);
function gamma(x: double): double; // ガンマ関数
var
i : integer;
sum : double;
xx, v : double;
xj : double;
lng : double;
ln_sqrt_2pi: double;
begin
ln_sqrt_2pi := ln(sqrt(2 * pi)); // = ln(2 * pi) / 2;
sum := 0;
v := 1;
while x < m do begin
v := v * x;
x := x + 1;
end;
xx := x * x;
xj := x;
lng := ln_sqrt_2pi - x + (x - 0.5) * ln(x) - ln(v);
for i := 1 to m do begin
sum := sum + B[i] / (i * 2 * (2 * i - 1)) / xj;
xj := xj * xx;
end;
result := exp(sum + lng);
end;
// γ(a, x)
function incomplete_gamma(a, x: double): double; // 第1種不完全ガンマ関数
var
k : integer;
term, previous : double;
begin
result := 0;
if x = 0 then exit;
term := exp(a * ln(x) - x) / a;
result := term;
for k := 1 to 1000 do begin
term := term * x / (a + k);
previous := result;
result := result + term;
if result = previous then begin
exit;
end;
end;
Form1.Memo1.Lines.add ('p_gamma(): 収束しません');
end;
// Γ(1/2, x^2) := gamma(1 / 2) - incomplete_gamma(1/2, x^2);
// γ(1/2, x^2) := incomplete_gamma(1/2, x^2);
function erf(x: double): double;
begin
result := incomplete_gamma(1 / 2 , x * x) / sqrt(pi);
// result := 1 - (gamma(1 / 2) - incomplete_gamma(1 / 2 , x * x)) / sqrt(pi);
end;
// 確率密度関数
function probability_density(u, x, s: double): double;
begin
result := 1 / sqrt(2 * pi * s * s) * exp(- (x - u) * (x - u) / 2 / s / s);
end;
// 下側累積分布す関数
function cumulative_distribution(u, x, s: double): double;
begin
result := (1 + erf((x - u) / sqrt(2 * s * s))) / 2;
if x < u then result := 1 - result;
end;
// 計算実行
procedure TForm1.BitBtn1Click(Sender: TObject);
var
x, u, s, xb: double;
fx, sx : double;
ch : integer;
dx, yb : double;
lng : double;
lfg : boolean;
col : Tcolor;
begin
val(LabeledEdit1.Text, u, ch);
if ch <> 0 then begin
application.MessageBox('平均値uに間違いがあります。','注意', 0);
exit;
end;
val(LabeledEdit2.Text, s, ch);
if ch <> 0 then begin
application.MessageBox('分散σに間違いがあります。','注意', 0);
exit;
end;
if s <= 0 then begin
application.MessageBox('分散σはゼロより大きくして下さい。','注意', 0);
exit;
end;
val(LabeledEdit3.Text, x, ch);
if ch <> 0 then begin
application.MessageBox('位置xに間違いがあります。','注意', 0);
exit;
end;
fx := probability_density(u, x, s);
sx := cumulative_distribution(u, x, s);
series1.Clear;
series2.Clear;
series3.Clear;
memo1.Clear;
memo1.Lines.Add('確率密度 ' + floatTostr(fx));
memo1.Lines.Add('下側累積確率 ' + floatTostr(sx));
memo1.Lines.Add('上側累積確率 ' + floatTostr(1 - sx));
if checkbox1.Checked = false then series2.AddXY(x, fx)
else series2.AddXY(x, sx);
lng := 4 * (trunc(s / 1.2) + 1);
if abs(x) + abs(u) > lng - 1 then lng := abs(x) + abs(u) + 1;
dx := lng / 100;
if checkbox1.Checked = false then begin
yb := 0;
series3.AddXY(-lng, yb);
lfg := false;
for ch := -100 to 100 do begin
xb := dx * ch;
fx := probability_density(u, xb, s);
if (not lfg) then begin
if (xb <= x) then col := clRed else col := clBlue;
series3.AddXY(xb, fx,'', col);
series3.AddXY(xb, 0,'', col);
series3.AddXY(xb + dx, 0,'', col);
end;
series1.AddXY(xb, fx);
if lfg then lfg := false else lfg := true;
end;
end
else begin
for ch := -100 to 100 do begin
xb := dx * ch;
sx := cumulative_distribution(u, xb, s);
series1.AddXY(xb, sx);
end;
end;
end;
end.