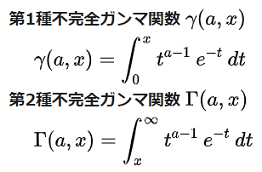
第1種不完全ガンマ関数は0~Xの不定積分で、第2種不完全ガンマ関数はX~∞の不定積分となります。
不完全ガンマ関数は、それ自身がそのまま使用されることは無く、分散や確率の計算に使用されます。
2020/08/26 C言語辞典の不完全ガンマ関数を修正したプログラムに第二種不完全ガンマ関数を直接計算するルーチンも修正追加しました。
不完全ガンマ関数
不完全ガンマ関数は、0~X と X~∞の不定積分です。
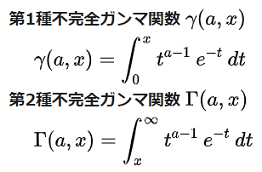
第1種不完全ガンマ関数は0~Xの不定積分で、第2種不完全ガンマ関数はX~∞の不定積分となります。
不完全ガンマ関数は、それ自身がそのまま使用されることは無く、分散や確率の計算に使用されます。
詳細は、ウィキペディア 不完全ガンマ関数 を参照してください。
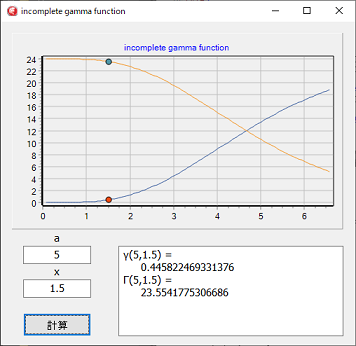
プログラム
次のプログラムはMathematics Source Library C & ASM にあった
incomplete_gamma_function.c をDelphiに変換したものです。
使用されていないルーチンや無駄なルーチンもあるので、他のプログラムに組み込む場合は、後述のプログラムの方が、小さく簡単です。
実行画面は、同じです。
//---------------------------------------------------------------- // http://www.mymathlib.com/functions/ // Mathematics Source Library C & ASM // gamma function convert C -> delphi //---------------------------------------------------------------- unit main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls, Vcl.Buttons, system.UITypes, VclTee.TeeGDIPlus, VCLTee.Series, VCLTee.TeEngine, VCLTee.TeeProcs, VCLTee.Chart; type TForm1 = class(TForm) BitBtn1: TBitBtn; LabeledEdit1: TLabeledEdit; LabeledEdit2: TLabeledEdit; Memo1: TMemo; Chart1: TChart; Series1: TLineSeries; Series2: TLineSeries; Series3: TPointSeries; Series4: TPointSeries; procedure FormCreate(Sender: TObject); procedure BitBtn1Click(Sender: TObject); private { Private 宣言 } function Gamma_Function(x: double): double; function xGamma_Function(x: extended): extended; function xGamma(x: extended): extended; function Duplication_Formula(two_x: extended): extended; function Gamma_Function_Max_Arg: double; function xGamma_Function_Max_Arg: extended; function Ln_Gamma_Function(x: double): double; function xLn_Gamma_Function(x: extended): extended; function xLnGamma_Asymptotic_Expansion(x: extended): extended; function Factorial(n: integer): double; function xFactorial(n :integer): extended; function Factorial_Max_Arg: integer; function Entire_Incomplete_Gamma_Function(x, nu: double): double; function xEntire_Incomplete_Gamma_Function(x, nu: extended): extended; function xSmall_x(x, nu: extended): extended; function xMedium_x(x, nu: extended): extended; function xLarge_x(x, nu: extended): extended; function Incomplete_Gamma_Function(x, nu: double): double; function xIncomplete_Gamma_Function(x, nu: extended): extended; public { Public 宣言 } end; var Form1: TForm1; implementation {$R *.dfm} uses math; const LONG_MAX = 2147483647; e = 2.71828182845904523536028747; exp_g_o_sqrt_2pi = 6.23316569877722552586386e+3; g = 9.65657815377331589457187; max_double_arg: double = 171.6243769; max_long_double_arg: extended = 1755.5; a: array[0..8] of extended = ( +1.14400529453851095667309e+4, -3.23988020152318335053598e+4, +3.50514523505571666566083e+4, -1.81641309541260702610647e+4, +4.63232990536666818409138e+3, -5.36976777703356780555748e+2, +2.28754473395181007645155e+1, -2.17925748738865115560082e-1, +1.08314836272589368860689e-4 ); //============================================================================= // // この関数はLanczosの式を使用して実際のGamma(x)を計算します。 // xの範囲は -(max_double_arg-1) < x < max_double_arg。 // ガンマ関数は複素平面で有理型であり、 // 正でない整数の値、xaの正の整数または半分の正の整数をテストすると、 // 約1.9e-16の最大絶対相対誤差です。 // x > max_double_argの場合、xGamma_Function(x)を使用する必要があります。 // または lnGamma(x) を計算します。 // x < 0の場合、ln(Gamma(x))は複素数になる可能性があることに注意してください。 // 複素数の計算はプログラムに組んでありません // 戻り値 // xが正で、max_double_argより小さい場合、Gamma(x)は // 返され、x> max_double_argの場合、maxdoubleが返されます。 // xが非正の整数、つまりxが極の場合、maxdoubleが返されます。 // (Gamma(x)は極の両側で符号を変更することに注意してください)。 // xが非正の非整数の場合 Gamma(x)> maxdouble場合、maxdoubleが返され、 // Gamma(x)<-maxdoubleの場合、-maxdoubleが返されます。 // //============================================================================= //================ ガンマ関数 =================== // Γ(x) function TForm1.Gamma_Function(x: double): double; var g: extended; maxx: double; begin maxx := max_double_arg; if x >= maxx then begin result := maxdouble; exit; end; g := xGamma_Function(x); if abs(g) < maxdouble then result := g else if g < 0 then result := -maxdouble else result := maxdouble; end; //============================================================================= // // この関数はLanczosの式を使用して実際のGamma(x)を計算します。 // xの範囲は -(max_long_double_arg-1) < x < max_long_double_arg。 // ガンマ関数は複素平面で有理型であり、正でない整数の値 // xaの正の整数または半分の正の整数をテストすると、 // 最大絶対相対誤差は約3.5e-16です。 // // x > max_long_double_argの場合、lnGamma(x)を使用する必要があります。 // x < 0 の場合、ln(Gamma(x)) は複素数になる可能性があることに注意してください。 // // 戻り値 // xが正で、max_long_double_argより小さい場合、Gamma(x) // が返され、x > max_long_double_argの場合、maxextendedが返されます。 // xが正でない整数の場合、maxextendedが // 返されます(Gamma(x)は値の両側で符号を変更することに注意してください)。 // xが非正の非整数の場合でx>-(max_long_double_arg + 1)の場合 // Gamma(x)が返されます。それ以外の場合は0.0が返されます // //============================================================================= function TForm1.xGamma_Function(x: extended): extended; var sin_x: extended; rg: extended; ix: int64; begin if x > 0 then if x <= max_long_double_arg then begin result := xGamma(x); exit; end else begin result := maxextended; exit; end; if x > -LONG_MAX then begin ix := round(x); if x = ix then begin result := maxextended; exit; end; end; sin_x := sin(pi * x); if sin_x = 0 then begin result := maxextended; exit; end; if x < - max_long_double_arg - 1 then begin result := 0; exit; end; rg := xGamma(1 - x) * sin_x / pi; if rg <> 0 then result := 1 / rg else result := maxextended; end; //============================================================================= // // この関数はLanczosの式を使用して実際のGamma(x)を計算します。 // x、ここで0<x<=900。900<x<1755.5の場合、倍数公式を使用します。 // 関数power()。結果の相対誤差は約10^-16です。x = 0付近を除きます。 // x>1755.5の場合、lnGamma(x)を計算する必要があります。 // xが正で1755.5未満の場合、Gamma(x)が返され、 // x>1755.5の場合、maxextendedが返されます。 // //============================================================================= function TForm1.xGamma(x: extended): extended; var xx: extended; temp: extended; n, i: integer; xx2 : extended; begin if x < 1 then xx := x + 1 else xx := x; n := sizeof(a) div sizeof(extended); if x > max_long_double_arg then begin result := maxextended; exit; end; if x > 900 then begin result := Duplication_Formula(x); exit; end; temp := 0; for i := n - 1 downto 0 do temp := temp + a[i] / (xx + i); temp := temp + 1; xx2 := (xx - 0.5) / 2; temp := temp * (power((g + xx - 0.5) / e, xx2) / exp_g_o_sqrt_2pi ); temp := temp * power((g + xx - 0.5) / e, xx2); // X64 オーバーフロー対策 if x < 1 then result := temp / x else result := temp; end; //============================================================================= // // この関数は倍数公式を使用してGamma(two_x)を返します。 // //============================================================================= function TForm1.Duplication_Formula(two_x: extended): extended; var x: extended; g: extended; n: integer; begin x := 0.5 * two_x; n := round(two_x) - 1; g := power(2.0, two_x - 1.0 - n); g := g * power(2, n); g := g / sqrt(pi); g := g * xGamma_Function(x); g := g * xGamma_Function(x + 0.5); result := g; end; //============================================================================= // // この関数は、Gamma_Functionの最大引数を返します。 // Gamma_Functionは引数が1より大きい場合、< maxdoubleという数値が返されます。 // //============================================================================= function TForm1.Gamma_Function_Max_Arg: double; begin result := max_double_arg; end; //============================================================================= // // この関数は、xGamma_Functionの最大引数を返します。 // xGamma_Functionは引数が1より大きい場合、< maxextendedという数値が返されます。 // //============================================================================= function TForm1.xGamma_Function_Max_Arg: extended; begin result := max_long_double_arg; end; //***************************************************************************** //============================================================================= // // 正の実数xに対するGamma(x)の自然対数を計算します。 // //============================================================================= //============================================================================= // Ln_Gamma_Function(x) および xLn_Gamma_Function(x) // // Gamma_Function_Max_Arg = 171とすると、 // 0 < x <= 171の場合、ln(gamma(x))は、Gamma_Function(x)からの結果。 // x> 171の場合、ln(gamma(x)は漸近展開を使用して計算されます。 // ln(gamma(x)〜ln(2sqrt(2pi))-x + (x-1/2)ln x + // B[2j] / [2j *(2j-1)* x^(2j-1)]の合計、 // 合計 jは1から3で、B[2j]は2j番目のベルヌーイ数です。 // //============================================================================= function TForm1.Ln_Gamma_Function(x: double): double; begin // 正の引数の 0 <x <= Gamma_Function_Max_Arg // の場合、Log(Gamma(x)を返します。 if x <= Gamma_Function_Max_Arg then result := ln(Gamma_Function(x)) //そうでない場合は、ln Gamma(x) の漸近展開から結果を返します。 else result := xLnGamma_Asymptotic_Expansion(x); end; //============================================================================= // // 正の実数のGamma(x)の自然対数を計算します // // Gamma_Function_Max_Arg = 171とすると、 // 0 <x <= 171の場合、ln(gamma(x))は // Gamma_Function(x)からの結果の値。 // x> 171の場合、ln(gamma(x)) は漸近展開を使用して計算されます。 // ln(gamma(x))〜ln(2sqrt(2pi))-x +(x-1/2)ln x + // B[2j] / [2j *(2j-1)* x^(2j-1)]の合計、 // 合計 jは1から3で、B[2j]は2j番目のベルヌーイ数です。 // //============================================================================= function TForm1.xLn_Gamma_Function(x: extended): extended; begin // 正の引数の場合、0 <x <= Gamma_Function_Max_Arg() // の場合、LogGamma(x)を返します。 if x <= xGamma_Function_Max_Arg then result := ln(xGamma_Function(x)) // そうでない場合は、ln Gamma(x) の漸近展開から結果を返します。 else result := xLnGamma_Asymptotic_Expansion(x); end; //============================================================================= // // この関数は、漸近を評価することでlog(gamma(x)を推定します // // ln(Gamma(x))〜ln(2sqrt(2pi))-x +(x-1/2)ln(x) + // B[2j] / [2j *(2j-1)* x^(2j-1)]の合計、 // 合計 jは1から3で、B[2j]は2j番目のベルヌーイ数です。 // //============================================================================= const log_sqrt_2pi = 9.18938533204672741780329736e-1; //ベルヌーイ数B(2)、B(4)、B(6)、...、B(20) B : array[0..9] of extended = ( 1.0 / (6 * 2 * 1), -1.0 / (30 * 4 * 3), 1.0 / (42 * 6 * 5), -1.0 / (30 * 8 * 7), 5.0 / (66 * 10 * 9), -691.0 / (2730 * 12 * 11), 7.0 / (6 * 14 * 13), -3617.0 / (510 * 16 * 15), 43867.0 / (798 * 18 * 17), -174611.0 / (330 * 20 * 19)); m: integer = sizeof(B) div sizeof(extended); function TForm1.xLnGamma_Asymptotic_Expansion(x: extended): extended; //const // m = 3; // 3で十分な精度が得られます。 var i : integer; term: array[0..9] of extended; sum : extended; xx : extended; xj : extended; lngamma : extended; begin sum := 0; xx := x * x; xj := x; lngamma := log_sqrt_2pi - xj + (xj - 0.5) * ln(xj); for i := 0 to m - 1 do begin term[i] := B[i] / xj; xj := xj * xx; end; for i := m - 1 downto 0 do sum := sum + term[i]; result := lngamma + sum; end; //============================================================================== //////////////////////////////////////////////////////////////////////////////// // 階乗 ルーチン: // // xFactorial // // Factorial_Max_Arg // //////////////////////////////////////////////////////////////////////////////// //////////////////////////////////////////////////////////////////////////////// // 関数Factorial(n)およびxFactorial(n)はn!を返します。 // // 0 <= n <= Factorial_Max_Arg()の場合。n> Factorial_Max_Argの場合、 // // 次にDBL_MAXが返され、n <0の場合は0が返されます。 // // 関数Factorial_Max_Argは最大引数を返します // // 関数FactorialおよびxFactorial。 // //////////////////////////////////////////////////////////////////////////////// const factorials: array [0..170] of extended = ( 1.000000000000000000000e+0, // 0! 1.000000000000000000000e+0, // 1! 2.000000000000000000000e+0, // 2! 6.000000000000000000000e+0, // 3! 2.400000000000000000000e+1, // 4! 1.200000000000000000000e+2, // 5! 7.200000000000000000000e+2, // 6! 5.040000000000000000000e+3, // 7! 4.032000000000000000000e+4, // 8! 3.628800000000000000000e+5, // 9! 3.628800000000000000000e+6, // 10! 3.991680000000000000000e+7, // 11! 4.790016000000000000000e+8, // 12! 6.227020800000000000000e+9, // 13! 8.717829120000000000000e+10, // 14! 1.307674368000000000000e+12, // 15! 2.092278988800000000000e+13, // 16! 3.556874280960000000000e+14, // 17! 6.402373705728000000000e+15, // 18! 1.216451004088320000000e+17, // 19! 2.432902008176640000000e+18, // 20! 5.109094217170944000000e+19, // 21! 1.124000727777607680000e+21, // 22! 2.585201673888497664000e+22, // 23! 6.204484017332394393600e+23, // 24! 1.551121004333098598400e+25, // 25! 4.032914611266056355840e+26, // 26! 1.088886945041835216077e+28, // 27! 3.048883446117138605015e+29, // 28! 8.841761993739701954544e+30, // 29! 2.652528598121910586363e+32, // 30! 8.222838654177922817726e+33, // 31! 2.631308369336935301672e+35, // 32! 8.683317618811886495518e+36, // 33! 2.952327990396041408476e+38, // 34! 1.033314796638614492967e+40, // 35! 3.719933267899012174680e+41, // 36! 1.376375309122634504632e+43, // 37! 5.230226174666011117600e+44, // 38! 2.039788208119744335864e+46, // 39! 8.159152832478977343456e+47, // 40! 3.345252661316380710817e+49, // 41! 1.405006117752879898543e+51, // 42! 6.041526306337383563736e+52, // 43! 2.658271574788448768044e+54, // 44! 1.196222208654801945620e+56, // 45! 5.502622159812088949850e+57, // 46! 2.586232415111681806430e+59, // 47! 1.241391559253607267086e+61, // 48! 6.082818640342675608723e+62, // 49! 3.041409320171337804361e+64, // 50! 1.551118753287382280224e+66, // 51! 8.065817517094387857166e+67, // 52! 4.274883284060025564298e+69, // 53! 2.308436973392413804721e+71, // 54! 1.269640335365827592597e+73, // 55! 7.109985878048634518540e+74, // 56! 4.052691950487721675568e+76, // 57! 2.350561331282878571829e+78, // 58! 1.386831185456898357379e+80, // 59! 8.320987112741390144276e+81, // 60! 5.075802138772247988009e+83, // 61! 3.146997326038793752565e+85, // 62! 1.982608315404440064116e+87, // 63! 1.268869321858841641034e+89, // 64! 8.247650592082470666723e+90, // 65! 5.443449390774430640037e+92, // 66! 3.647111091818868528825e+94, // 67! 2.480035542436830599601e+96, // 68! 1.711224524281413113725e+98, // 69! 1.197857166996989179607e+100, // 70! 8.504785885678623175212e+101, // 71! 6.123445837688608686152e+103, // 72! 4.470115461512684340891e+105, // 73! 3.307885441519386412260e+107, // 74! 2.480914081139539809195e+109, // 75! 1.885494701666050254988e+111, // 76! 1.451830920282858696341e+113, // 77! 1.132428117820629783146e+115, // 78! 8.946182130782975286851e+116, // 79! 7.156945704626380229481e+118, // 80! 5.797126020747367985880e+120, // 81! 4.753643337012841748421e+122, // 82! 3.945523969720658651190e+124, // 83! 3.314240134565353266999e+126, // 84! 2.817104114380550276949e+128, // 85! 2.422709538367273238177e+130, // 86! 2.107757298379527717214e+132, // 87! 1.854826422573984391148e+134, // 88! 1.650795516090846108122e+136, // 89! 1.485715964481761497310e+138, // 90! 1.352001527678402962552e+140, // 91! 1.243841405464130725548e+142, // 92! 1.156772507081641574759e+144, // 93! 1.087366156656743080274e+146, // 94! 1.032997848823905926260e+148, // 95! 9.916779348709496892096e+149, // 96! 9.619275968248211985333e+151, // 97! 9.426890448883247745626e+153, // 98! 9.332621544394415268170e+155, // 99! 9.332621544394415268170e+157, // 100! 9.425947759838359420852e+159, // 101! 9.614466715035126609269e+161, // 102! 9.902900716486180407547e+163, // 103! 1.029901674514562762385e+166, // 104! 1.081396758240290900504e+168, // 105! 1.146280563734708354534e+170, // 106! 1.226520203196137939352e+172, // 107! 1.324641819451828974500e+174, // 108! 1.443859583202493582205e+176, // 109! 1.588245541522742940425e+178, // 110! 1.762952551090244663872e+180, // 111! 1.974506857221074023537e+182, // 112! 2.231192748659813646597e+184, // 113! 2.543559733472187557120e+186, // 114! 2.925093693493015690688e+188, // 115! 3.393108684451898201198e+190, // 116! 3.969937160808720895402e+192, // 117! 4.684525849754290656574e+194, // 118! 5.574585761207605881323e+196, // 119! 6.689502913449127057588e+198, // 120! 8.094298525273443739682e+200, // 121! 9.875044200833601362412e+202, // 122! 1.214630436702532967577e+205, // 123! 1.506141741511140879795e+207, // 124! 1.882677176888926099744e+209, // 125! 2.372173242880046885677e+211, // 126! 3.012660018457659544810e+213, // 127! 3.856204823625804217357e+215, // 128! 4.974504222477287440390e+217, // 129! 6.466855489220473672507e+219, // 130! 8.471580690878820510985e+221, // 131! 1.118248651196004307450e+224, // 132! 1.487270706090685728908e+226, // 133! 1.992942746161518876737e+228, // 134! 2.690472707318050483595e+230, // 135! 3.659042881952548657690e+232, // 136! 5.012888748274991661035e+234, // 137! 6.917786472619488492228e+236, // 138! 9.615723196941089004197e+238, // 139! 1.346201247571752460588e+241, // 140! 1.898143759076170969429e+243, // 141! 2.695364137888162776589e+245, // 142! 3.854370717180072770522e+247, // 143! 5.550293832739304789551e+249, // 144! 8.047926057471991944849e+251, // 145! 1.174997204390910823948e+254, // 146! 1.727245890454638911203e+256, // 147! 2.556323917872865588581e+258, // 148! 3.808922637630569726986e+260, // 149! 5.713383956445854590479e+262, // 150! 8.627209774233240431623e+264, // 151! 1.311335885683452545607e+267, // 152! 2.006343905095682394778e+269, // 153! 3.089769613847350887959e+271, // 154! 4.789142901463393876336e+273, // 155! 7.471062926282894447084e+275, // 156! 1.172956879426414428192e+278, // 157! 1.853271869493734796544e+280, // 158! 2.946702272495038326504e+282, // 159! 4.714723635992061322407e+284, // 160! 7.590705053947218729075e+286, // 161! 1.229694218739449434110e+289, // 162! 2.004401576545302577600e+291, // 163! 3.287218585534296227263e+293, // 164! 5.423910666131588774984e+295, // 165! 9.003691705778437366474e+297, // 166! 1.503616514864999040201e+300, // 167! 2.526075744973198387538e+302, // 168! 4.269068009004705274939e+304, // 169! 7.257415615307998967397e+306 // 170! ); NN: integer = sizeof(factorials) div sizeof(extended); ////////////////////////////////////////////////////////////////////////////////// // function Factorial(n: integer): // // この関数はn!を計算します0 <= n <= Factorial_Max_Arg()の場合。 // // n> Factorial_Max_Arg()の場合、DBL_MAXが返され、n <0の場合、0が返されます。 // // // //引数: // // n 階乗関数の引数。 // // // //戻り値: // // nが負の場合、0が返されます。n> Factorial_Max_Argの場合、DBL_MAXが返されます。// // 0 <= n <= Factorial_Max_Arg()の場合、 n!返されます。 // // // ////////////////////////////////////////////////////////////////////////////////// function TForm1.Factorial(n: integer): double; begin // For a negative argument (n < 0) return 0.0 // if n < 0 then begin result := 0.0; exit; end; // For a large postive argument (n >= N) return DBL_MAX // if n >= NN then begin result := Maxdouble; exit; end; // Otherwise return n!. result := factorials[n]; end; ///////////////////////////////////////////////////////////////////////////////// // function xFactorial(n : integer): extended; // // // // この関数はn!を計算します 0 <= n <= Factorial_Max_Arg()の場合 // // n> Factorial_Max_Arg()の場合、DBL_MAXが返され、n <0の場合、0が返されます。// // // // 戻り値: // // nが負の場合、0が返されます。n> Factorial_Max_Arg()の場合、 // // 次にDBL_MAXが返されます。0 <= n <= Factorial_Max_Arg()の場合、 // // n!返されます。 // ///////////////////////////////////////////////////////////////////////////////// function TForm1.xFactorial(n: integer): extended; begin // For a negative argument (n < 0) return 0.0 if n < 0 then begin result := 0.0; exit; end; // For a large postive argument (n >= N) return DBL_MAX if n >= NN then begin result := MaxDouble; exit; end; // Otherwise return n!. result := factorials[n]; end; //////////////////////////////////////////////////////////////////////////////// // function Factorial_Max_Arg: integer // // // // この関数は、Factial関数の最大引数を返します // //////////////////////////////////////////////////////////////////////////////// function TForm1.Factorial_Max_Arg: integer; begin result := NN - 1; end; //////////////////////////////////////////////////////////////////////////////// // Entire_Incomplete_Gamma_Function // // xEntire_Incomplete_Gamma_Function // // 不完全なガンマ関数全体。正規化とも呼ばれます // // 不完全なガンマ関数、0からxまでの積分として定義 // // 被積分関数t ^(nu-1)exp(-t)/ gamma(nu)dt。 // // パラメータnuは 形状パラメータと呼ばれることもあります。 // ////////////////////////////////////////////////// ///////////////////////////// ////////////////////////////////////////////////// ///////////////////////////// // function Entire_Incomplete_Gamma_Function(x,nu: double): double // // 引数 // // x : double 被積分関数で与えられる上限 // // nu: double不完全なガンマ関数全体の形状パラメーター。 // ////////////////////////////////////////////////// ///////////////////////////// function TForm1.Entire_Incomplete_Gamma_Function(x, nu: double): double; begin result := xEntire_Incomplete_Gamma_Function(x, nu); end; ////////////////////////////////////////////////// ////////////////////////////// // function xEntire_Incomplete_Gamma_Function(x、nu: extended): extended // // 不完全なガンマ関数全体。正規化とも呼ばれます // // 不完全なガンマ関数、0からxのxまでの積分として定義 // // 被積分関数 t ^(nu-1)exp(-t)/ gamma(nu)dt // // パラメータnuは 形状パラメータと呼ばれることもあります。 // // // // 引数: // // x: extended 上記の被積分関数を使用した積分の上限。 // // nu: extended 不完全なガンマ全体の形状パラメータ 。 // ////////////////////////////////////////////////// ////////////////////////////// function TForm1.xEntire_Incomplete_Gamma_Function(x, nu: extended): extended; begin if x = 0.0 then begin result := 0.0; exit; end; if abs(x) <= 1.0 then begin result := xSmall_x(x, nu); exit; end; if abs(x) < (nu + 1.0) then begin result := xMedium_x(x, nu); exit; end; result := xLarge_x(x, nu); end; ///////////////////////////////////////////////////////////////////////////////// // function xSmall_x(x、nu: extended): extended; // // // // この関数は、不完全なガンマ関数全体を近似します // // x、ここで -1 <= x <=1 // // 引数: // // x extended 被積分関数が記述された積分の上限 // // Entire_Incomplete_Gamma_Functionの下のセクション。 // // long double nu不完全なガンマ全体の形状パラメータ // // 戻り値: // // 不完全なガンマ関数全体: // // I(0、x)t ^(nu-1)Exp(-t)dt / Gamma(nu)。 // ///////////////////////////////////////////////////////////////////////////////// const Nterms= 20; function TForm1.xSmall_x(x, nu: extended): extended; var terms : array [0..Nterms - 1] of extended; x_term : extended; x_power : extended; sum : extended; i : integer; begin x_term := -x; x_power := 1.0; for i := 0 to Nterms - 1 do begin terms[i] := (x_power / xFactorial(i)) / (i + nu); x_power := x_power * x_term; end; sum := terms[Nterms-1]; for i := Nterms-2 downto 0 do sum := sum + terms[i]; if nu <= Gamma_Function_Max_Arg then result := power(x,nu) * sum / xGamma_Function(nu) else result := exp(nu * ln(x) + ln(sum) - xLn_Gamma_Function(nu)); end; //////////////////////////////////////////////////////////////////////////////// // function xMedium_x(x、nu: extended):extended // // // //この関数は、不完全なガンマ関数全体を近似します // // x、ここで 1 <x <nu +1 // // // // nu + 1 < xの場合、xLarge_x(x、nu)を使用する必要があります。 // // // // 引数: // // x : extended 被積分関数が記述された積分の上限 // // Entire_Incomplete_Gamma_Functionの下のセクション。 // // nu: extended 不完全なガンマ全体の形状パラメータ // // 戻り値: // // 不完全なガンマ関数全体: // // I(0、x)t ^(nu-1)exp(-t)dt / gamma(nu) // //////////////////////////////////////////////////////////////////////////////// var DBL_EPSILON : double; function TForm1.xMedium_x(x, nu: extended): extended; var coef : extended; term : extended; corrected_term : extended; temp_sum : extended; correction : extended; sum1 : extended; sum2 : extended; epsilon : extended; i : integer; begin term := 1.0 / nu; corrected_term := term; temp_sum := term; correction := -temp_sum + corrected_term; sum1 := temp_sum; epsilon := 0.0; if nu > Gamma_Function_Max_Arg then begin coef := exp(nu * ln(x) - x - xLn_Gamma_Function(nu)); if coef > 0.0 then epsilon := DBL_EPSILON / coef; end else begin coef := power(x, nu) * exp(-x) / xGamma_Function(nu); epsilon := DBL_EPSILON / coef; end; if epsilon <= 0.0 then epsilon := DBL_EPSILON; i := 1; while term > epsilon * sum1 do begin term := term * x / (nu + i); corrected_term := term + correction; temp_sum := sum1 + corrected_term; correction := (sum1 - temp_sum) + corrected_term; sum1 := temp_sum; inc(i); end; sum2 := sum1; sum1 := sum1 * coef; correction := correction + sum2 - sum1 / coef; term := term * x / (nu + i); sum2 := term + correction; inc(i); while term + correction > epsilon * sum2 do begin term := term * x / (nu + i); corrected_term := term + correction; temp_sum := sum2 + corrected_term; correction := (sum2 - temp_sum) + corrected_term; sum2 := temp_sum; inc(i); end; sum2 := sum2 + correction; sum2 := sum2 * coef; result := sum1 + sum2; end; ///////////////////////////////////////////////////////////////////////////////// // function xLarge_x(x、nu: extended) // // // // この関数は、不完全なガンマ関数全体を//近似します // // x、ここで nu + 1 <= x // // // // 0 <= x <nu + 1の場合、xSmall_x(x、nu)を使用する必要があります // // // // 引数: // // x: extended被積分関数が記述された積分の上限 // // Entire_Incomplete_Gamma_Functionの下のセクション // // nu: extended 不完全なガンマ全体の形状パラメータ // // 戻り値: // // xが正で171より小さい場合、Gamma(x)が返され // // x> 171の場合、MAXDoubleが返されます。 // ///////////////////////////////////////////////////////////////////////////////// function TForm1.xLarge_x(x, nu: extended): extended; var temp : extended; sum : extended; coef : extended; i : integer; n : integer; begin temp := 1.0 / nu; sum := temp; n := trunc(x - nu - 1.0) + 1; for i := 1 to n - 1 do begin temp := temp * x / (nu + i); sum := sum + temp; end; if nu <= Gamma_Function_Max_Arg then begin coef := power(x, nu) * exp(-x) / xGamma_Function(nu); result := xMedium_x(x, nu + n) + coef * sum; end else result := exp(ln(sum) + nu * ln(x) - x - xLn_Gamma_Function(nu)) + xMedium_x(x, nu + n); end; ///////////////////////////////////////////////////////////////////////////////// //ファイル:incomplete_gamma_function // // // // Incomplete_Gamma_Function // // xIncomplete_Gamma_Function // // 不完全なガンマ関数は0からxまでの積分として定義されます // // 被積分関数t ^(nu-1)exp(-t)dtのパラメータnuは // // 時々 形状パラメータと呼ばれます。 // ///////////////////////////////////////////////////////////////////////////////// ///////////////////////////////////////////////////////////////////////////////// // function Incomplete_Gamma_Function(x、nu: double):double; // // 引数: // // x: double 与えられた被積分関数を使った積分の上限 // // nu: double 不完全なガンマ関数の形状パラメーター // // // // 戻り値: // // 不完全なガンマ関数 Integral [0、x] t ^(nu-1)exp(-t)dt // ///////////////////////////////////////////////////////////////////////////////// function TForm1.Incomplete_Gamma_Function(x, nu: double): double; begin result := xIncomplete_Gamma_Function(x, nu); end; //////////////////////////////////////////////////////////////////////////////// // function xIncomplete_Gamma_Function(x、nu: extended): extended; // // // // 不完全なガンマ関数は0からxまでの積分として定義されます // // 被積分関数t ^(nu-1)exp(-t)dtのパラメータnuは時々 // // 形状パラメータと呼ばれます。 // // // // 引数: // // x : extended 上記の被積分関数を使用した積分の上限 // // nu : extended 不完全なガンマ関数の形状パラメーター // // // // 戻り値: // // 不完全なガンマ関数 Integral [0、x] t ^(nu-1)exp(-t)dt。 // //////////////////////////////////////////////////////////////////////////////// function TForm1.xIncomplete_Gamma_Function(x, nu: extended): extended; begin if x = 0.0 then begin result := 0.0; exit; end; if nu <= Gamma_Function_Max_Arg then result := xEntire_Incomplete_Gamma_Function(x, nu) * xGamma_Function(nu) else result := exp(ln(xEntire_Incomplete_Gamma_Function(x,nu)) + xLn_Gamma_Function(nu)); end; ////////////////////////////////////////////////////////////////////// // // // DBL_EPSILONの設定 // // // // 1に加算して1以上になる一番小さい値を計算します // ////////////////////////////////////////////////////////////////////// procedure TForm1.FormCreate(Sender: TObject); var i : integer; y, z : double; begin i := 0; z := 1; DBL_EPSILON := 1; repeat DBL_EPSILON := DBL_EPSILON / 2; y := z + DBL_EPSILON; inc(i); until (y = 1) or (i > 70); DBL_EPSILON := DBL_EPSILON * 2; end; //============================== // 入力値計算とグラフ作図 //============================== procedure TForm1.BitBtn1Click(Sender: TObject); var ch : integer; x, nu: double; GI, G : double; MIN, MAX: double; dx : double; i : integer; begin val(LabeledEdit1.Text, x, Ch); if ch <> 0 then begin MessageDlg('xの値に間違いがあります。', mtInformation, [mbOk], 0, mbOk); exit; end; if x < 0 then begin MessageDlg('負数のxは計算出来ません', mtInformation, [mbOk], 0, mbOk); exit; end; val(LabeledEdit2.Text, nu, Ch); if ch <> 0 then begin MessageDlg('aの値に間違いがあります。', mtInformation, [mbOk], 0, mbOk); exit; end; if nu <= 0 then begin MessageDlg('aはゼロより大きくして下さい計算出来ません。', mtInformation, [mbOk], 0, mbOk); exit; end; GI := Incomplete_Gamma_Function(x, nu); G := Gamma_Function(nu); Memo1.Clear; Memo1.Lines.Add('γ(' + floatTostr(nu) + ',' + floatTostr(x) + ') = '); Memo1.Lines.Add(' ' + floatTostr(GI)); Memo1.Lines.Add('Γ(' + floatTostr(nu) + ',' + floatTostr(x) + ') = '); Memo1.Lines.Add(' ' + floatTostr(G - GI)); Series1.Clear; Series2.Clear; Series3.Clear; Series4.Clear; Series3.AddXY(x, GI); Series4.AddXY(x, G - GI); MIN := x / 20; MAX := MIN + x + 5; dx := (MAX - MIN) / 100; for i := 0 to 100 do begin x := dx * i + min; GI := Incomplete_Gamma_Function(x, nu); Series1.AddXY(x, GI); Series2.AddXY(x, G - GI); end; end; end.
次のプログラムは、C言語辞典にある不完全ガンマ関数を修正したものです。
C言語辞典では、第1種不完全ガンマ関数の使用例となっていますので、第1種不完全ガンマ関数部分を取り出し、
第2種はガンマ関数から第1種を差し引いて計算する方法と、 x の値が 1 + a より大きい場合は、 第2種不完全ガンマ関数を直接計算する方法を選択出来るようにしています。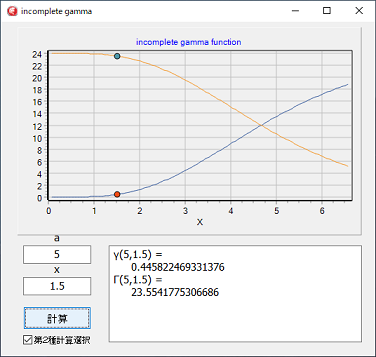
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, VclTee.TeeGDIPlus,
VCLTee.Series, VCLTee.TeEngine, Vcl.ExtCtrls, VCLTee.TeeProcs, VCLTee.Chart,
Vcl.Buttons, system.UITypes;
type
TForm1 = class(TForm)
Memo1: TMemo;
LabeledEdit1: TLabeledEdit;
BitBtn1: TBitBtn;
LabeledEdit2: TLabeledEdit;
Chart1: TChart;
Series1: TLineSeries;
Series2: TLineSeries;
Series3: TPointSeries;
Series4: TPointSeries;
procedure BitBtn1Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
const
//ベルヌーイ数B(2)、B(4)、B(6)、...、B(16)
B : array[1..8] of double = ( 1.0 / 6, // B(2)
-1.0 / 30,
1.0 / 42,
-1.0 / 30,
5.0 / 66,
-691.0 / 2730,
7.0 / 6,
-3617.0 / 510); // B(16)
m: integer = sizeof(B) div sizeof(double);
function Gamma(x: double): double; // ガンマ関数
var
i : integer;
sum : double;
xx, v : double;
xj : double;
lng : double;
ln_sqrt_2pi: double;
begin
ln_sqrt_2pi := ln(sqrt(2 * pi)); // = ln(2 * pi) / 2;
sum := 0;
v := 1;
while x < m do begin
v := v * x;
x := x + 1;
end;
xx := x * x;
xj := x;
lng := ln_sqrt_2pi - x + (x - 0.5) * ln(x) - ln(v);
for i := 1 to m do begin
sum := sum + B[i] / (i * 2 * (2 * i - 1)) / xj;
xj := xj * xx;
end;
result := exp(sum + lng);
end;
// γ(a, x)
function incomplete_gamma(a, x: double): double; // 第1種不完全ガンマ関数
var
k : integer;
term, previous : double;
begin
result := 0;
if x = 0 then exit;
term := exp(a * ln(x) - x) / a;
result := term;
for k := 1 to 1000 do begin
term := term * x / (a + k);
previous := result;
result := result + term;
if result = previous then begin
exit;
end;
end;
Form1.Memo1.Lines.add ('p_gamma(): 収束しません');
end;
// Γ(a, x)
function incomplete_gamma2(a, x: double): double; // 第2種不完全ガンマ関数
var
k : integer;
w, temp, previous : double;
la, lb : double;
begin
if x < 1 + a then begin
result := Gamma(a) - incomplete_gamma1(a, x);
exit;
end;
la := 1; // Laguerreの多項式
lb := 1 + x - a;
w := exp(a * ln(x) - x);
result := w / lb;
for k := 2 to 1000 do begin
temp := ((k - 1 - a) * (lb - la) + (k + x) * lb) / k;
la := lb;
lb := temp;
w := w * (k - 1 - a) / k;
temp := w / (la * lb);
previous := result;
result := result + temp;
if result = previous then exit;
end;
Form1.Memo1.Lines.add ('q_gamma: 収束しません');
end;
procedure TForm1.BitBtn1Click(Sender: TObject);
var
ch : integer;
x, a: double;
GI, G : double;
MIN, MAX: double;
dx : double;
i : integer;
begin
val(LabeledEdit1.Text, x, Ch);
if ch <> 0 then begin
MessageDlg('xの値に間違いがあります。', mtInformation,
[mbOk], 0, mbOk);
exit;
end;
if x < 0 then begin
MessageDlg('負数のxは計算出来ません', mtInformation,
[mbOk], 0, mbOk);
exit;
end;
val(LabeledEdit2.Text, a, Ch);
if ch <> 0 then begin
MessageDlg('aの値に間違いがあります。', mtInformation,
[mbOk], 0, mbOk);
exit;
end;
if a <= 0 then begin
MessageDlg('aはゼロより大きくして下さい計算出来ません。', mtInformation,
[mbOk], 0, mbOk);
exit;
end;
GI := incomplete_gamma(a, x);
if checkbox1.Checked = false then
G := gamma(a) - GI
else
G := incomplete_gamma2(a, x);
Memo1.Clear;
Memo1.Lines.Add('γ(' + floatTostr(a) + ',' + floatTostr(x) + ') = ');
Memo1.Lines.Add(' ' + floatTostr(GI));
Memo1.Lines.Add('Γ(' + floatTostr(a) + ',' + floatTostr(x) + ') = ');
Memo1.Lines.Add(' ' + floatTostr(G));
Series1.Clear;
Series2.Clear;
Series3.Clear;
Series4.Clear;
Series3.AddXY(x, GI);
Series4.AddXY(x, G);
MIN := x / 20;
MAX := MIN + x + 5;
dx := (MAX - MIN) / 100;
for i := 0 to 100 do begin
x := dx * i + MIN;
GI := incomplete_gamma(a, x);
Series1.AddXY(x, GI);
if checkbox1.Checked = false then
G := gamma(a) - GI
else
G := incomplete_gamma2(a, x);
Series2.AddXY(x, G);
end;
end;
end.