簡単な有限要素法

　有限要素法の計算は、インターネットで検索すれば、沢山紹介されています。
しかし、実際に計算をしてみないと、どのような物かわかりません、とは言っても、実際にプログラムを組むのは、面倒でしょう。
ここには、有限要素法の簡単なプログラムが収録されています。
計算の方法については、参考書、インターネットを参照して下さい、収録してあるプログラムは、１９８６年頃に、参考書を見ながら、入力したものです。
圧縮ファイルに入っているのは、立体トラス、二次元の三角薄板モード、ラーメン　二次元の振動解析、二次元の三角薄板モード用再分割ソフトです。
　ラーメンには、使用方法のヘルプファイルも入っています。
　ここにあるプログラムを作成した時代は、パソコンに搭載されているメモリーの容量は数Mバイト程度の時代のものです、計算速度も今の百分の一以下でした。
要素数を、少し多くすると、メモリーが足りなくなるか、計算が終わるのに一時間も二時間も掛かり、バグで計算が終わらないのか、時間が掛かっているだけなのか判別がつかない事もありました。
　各プログラムには、データーを入力しなくても、試し計算が出来る様にテストモードを設定してあります、それを実行してみれば、何を入力すれば良いのか分かるでしょう。

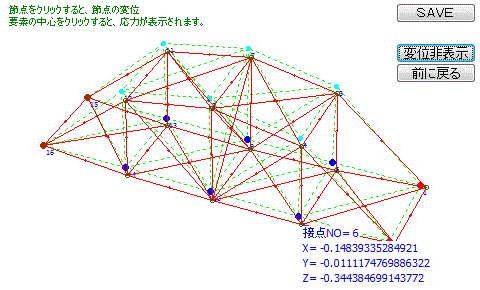
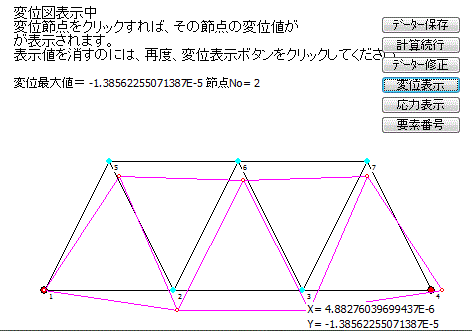　左図は、薄板モードの計算結果のグラフィック出力例です。
このモードは、均一荷重による圧縮の場合は、精度良く結果が出ますが、曲げに関しては、要素数をかなり増やしても、解に近づきません。
この時代の参考書には、計算結果が、あまり変化しなくなるまで要素の数を増やすようにと、書いてありました。しかし、前にも書いたように、メモリーは少ない、計算は遅いで、実用に使用するのはあきらめました。
２０００年台に入ると、メモリーも飛躍的増え、計算速度も早くなったので、再度確認をしましたが、曲げに関しては、要素数を信じられないぐらい多くしないと理論解に近づきません、やはり、実用にはほど遠いものでした。
計算精度を７０％程度と割り切ってしまえば良いのかも知れませんが。
　再度確認といっても、最初はＮ８８ＢＡＳＩＣで、次はＭＳＢＡＳＩＣ、Ｗｉｎｄｏｗｓになってからは、Ｃ、ＶＢとなり、現在はＤｅｌｐｈｉを使用しています。
Ｃ、ＶＢは、ほんの僅かの期間しか使用する事はありませんでした、Ｄｅｌｐｈｉの方が技術計算のプログラムを作るのに、相性が良かったからです。
とにかく、言語を変える度に入力しなおしとなりました。
　トラス、ラーメンの計算は、剛性としてを要素材料のデーターがそのまま使用されるので、微小たわみの計算結果は、理論解とほぼ同じ結果となります。
微小たわみが、理論解と同じになれば、大たわみの計算は、荷重を分割して繰り返し計算すれば、かなり解に近似した結果を得ることが出来ます。

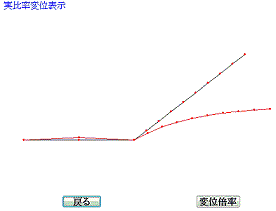　左図はラーメン計算で板バネの先端に上から荷重を掛け、荷重を分割して計算した結果あらわしてますが、かなり、理論解に近い結果となっています。

　板バネの先端に回転荷重をかけ３００分割して計算すると、きれいな円弧撓みとして決算結果が表示されました。
実際の撓みに非常に近い結果となっています。
ラーメンの場合、要素数をあまり増やさなくても、良い結果が得られ、実用になるようです。
そこで、ラーメンの計算ソフトには、要素のデーターを容易に入力出来るように、材料名を選択することにより、その材料の特性値を自動的に入力する機能と、断面形状を選んで、その寸法を入力すれば、断面二次モーメント、断面係数、面積を計算するルーチンが組み込んであります。
これで、かなり入力の手間を省略することが出来ています。

　トラスについては、筆者の仕事上で使う機会がなかったので、確認をしていません。
立体トラスのグラフィック表示は三次元で、マウスで視点を自由に変えられるようになっています、但しＺ軸は固定です。
　二次元の振動解析についても、薄板モードに関しては、圧縮方向の振動周波数はかなり一致しますが、曲げ方向の周波数は高い値となり一致しません。
当然、要素の数を多くすれば近い値にはなりますが、振動解析は計算に時間がかかります。
テストデーターを保存し、マージソフトで再分割し、要素数を増やし、順次計算をしてみれば良いでしょう。

　Finite_Element_Method_A.zip

各種プログラム計算例に戻る