誤差関数(Error function)
ガウスの誤差関数
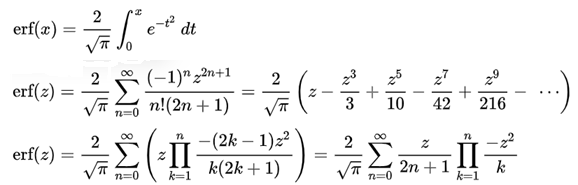
一番上の式が誤差関数の定義で、次はテイラー級数です。
三番目の計算式がありますが、プログラム的には。二番目の式のΣの中の分子を ｚ (－ｚ2)ｎにした方が計算効率が良いように思われますのでプログラムはｚ
(－ｚ2)ｎで作成してあります。
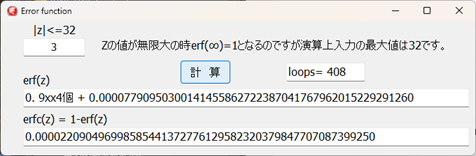左図は、此処での誤差関数計算プログラムを実行した場合のものですが、誤差関数の値は、zの値が無限大で誤差関数の値は1になるのですが、Zの値が10.7程度で50桁表示でerf(z)の表示値が"1"になってしまいます。
erfc(z)の値を観れば、"1"で無いことはわかるのですが、勘違いを防ぐために、9の数＋9以後の値として表示する様にしました。
通常の表示も可能です。
例 0.99532226501895273416206925636725292861089179704006 = 0.9xx2 +
0.00532226501895273416206925636725292861089179704006
0.99999998458274209971998114784032651311595142785475 = 0.9xx7 +
8.458274209971998114784032651311595142785475e-8
の様な表示なります。
ｚの値は、複素数でも良いらしいのですが、プログラムは複素数には対応していません。
又、プログラムの現在のｚの値の最大の入力値は32ですが、これを大きくする為には、有効桁数大きくすることと、収束判定値を小さくする必要があります。
収束判定値は、EPSCの値と同時にpi_biig functonの左シフトの値を変更する必要があります。
演算の有効桁数は、除算時の有効桁数なのですが、乗算や加減算では有効桁数に丸められる事は無いので適時丸める必要があります。
特に、除算前には、有効桁数を揃えないと、正常に除算が行われないことがあります。
プログラム
Biginteger & Bigdecimal の組み込み方は第１種ケルビン関数を参照して下さい。
unit main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls, system.UITypes;
type
TForm1 = class(TForm)
zEdit: TLabeledEdit;
calcBtn: TButton;
ansREdit: TLabeledEdit;
nEdit: TEdit;
OneMansEdit: TLabeledEdit;
Label1: TLabel;
CheckBox1: TCheckBox;
procedure calcBtnClick(Sender: TObject);
procedure FormCreate(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses Velthuis.BigIntegers, Velthuis.Bigdecimals;
const
EPSC = '1e-500'; // 収束反対値
DPS = 1000; // 除算有効桁数
precisions : integer = DPS; // 有効桁数
ZINMAX = '32'; // |z|の入力最大値 有効桁数と収束判定値の関係での値
// 有効桁数が不足、収束判定値が大きいと演算結果が
// 1.0を超えます。
//------------------------------------------------------------------------------
// π
// https://www.kurims.kyoto-u.ac.jp/~ooura/pi_fft-j.html
// T.Ooura AGM アルゴリズ
function pi_big: Bigdecimal;
var
n, dpcs : integer;
rmback : BigDecimal.RoundingMode;
SQRT_SQRT_EPSILON, c, b, e : BigDecimal;
npow : Bigdecimal;
a, one, two, four, five, eight : Bigdecimal;
begin
rmBack := BigDecimal.DefaultRoundingMode; // 除算丸めモードバックアップ
dpcs := precisions + 5; // 指定精度 + α
BigDecimal.DefaultPrecision := dpcs;
BigDecimal.DefaultRoundingMode := rmNearesteven;
one := '1';
one := one.RoundToPrecision(dpcs); // oneの有効桁数をdpcsに設定
two := '2';
four := '4';
five := '5';
eight := '8';
SQRT_SQRT_EPSILON := one / BigDecimal.IntPower(two, dpcs shl 1); // 収束判定値
c := BigDecimal.Sqrt(one / eight, dpcs * 2);
a := one + c + c + c;
b := BigDecimal.Sqrt(a, dpcs * 2);
e := b - five / eight;
b := b + b;
c := e - c;
a := a + e;
npow := '4';
n := 0;
while (e > SQRT_SQRT_EPSILON) and (n < 100) do begin
npow := npow + npow; // 8,16,32,64
e := (a + b) / two; // 平均値 除算有効桁数での丸め
b := a * b;
b := b.RoundToPrecision(dpcs); // pcs + α 丸め
b := BigDecimal.Sqrt(b, dpcs * 2); // 平方根有効桁数での丸め
e := e - b;
b := b + b;
c := c - e;
a := e + b;
inc(n);
end;
e := e * e;
e := e.RoundToPrecision(dpcs); // pcs + α 丸め
e := e / four; // e = e * e / 4
a := a + b;
result := (a * a - e - e / two) / (a * c - e) / npow; // 除算の順番に注意
result := result.RoundToPrecision(precisions); // 指定の精度に丸め
BigDecimal.DefaultPrecision := precisions; // 除算演算精度復帰
BigDecimal.DefaultRoundingMode := rmBack; // 除算丸めモード復帰
end;
//------------------------------------------------------------------------------
// erf(z)
function Error_function(z : bigdecimal): bigdecimal;
var
mzh2, zhn, s, tmp : bigdecimal;
epsilon, pai2, sabs : bigdecimal;
one, two, n, nl, nn : bigdecimal;
dpcs : integer;
begin
dpcs := precisions; // 除算有効桁数
epsilon := EPSC; // 収束判定値
one := bigdecimal.One; // 1
two := one + one; // 2
pai2 := pi_big; // π
pai2 := two / pai2.Sqrt(pai2, dpcs + dpcs); // 2/√(π)
mzh2 := -z * z; // -z^2
s := z; // n = 0時 z
nl := one; // 0! = 1
zhn := z; // n = 0時 z
n := one; // n=1から
repeat
nn := n + n + one; // 2n+1
nn := nn * nl; // n!(2n+1)
zhn := zhn * mzh2; // ((-1)^n)(z^(2n+1))
nn := nn.RoundToPrecision(dpcs); // 除算前桁合わせ
zhn := zhn.RoundToPrecision(dpcs); // 除算前桁合わせ
tmp := zhn / nn; // ((-1)^n)(z^(2n+1))/(n!(2n+1))
s := s + tmp; // Σ+Δ
n := n + one; // inc(n)
nl := nl * n; // n!
sabs := tmp.Abs(tmp); // |Δ|
until sabs < epsilon;
result := s * pai2; // Σ* 2/√(π)
form1.nedit.Text := 'loops= ' + n.ToString;
end;
//------------------------------------------------------------------------------
// 答0.99・9xxxの9の値を数えると同時に元の値から0.99・9xxx-0.99・9で0.00・xxxを得ます。
function nineNo(x : bigdecimal; var ans: bigdecimal): integer;
const
NINE = '9';
var
char9 : char;
i, lng, count : integer;
str, ninestr : string;
s9f : boolean;
nines : bigdecimal;
begin
s9f := false;
char9 := NINE;
str := x.ToPlainString;
lng := length(str);
ninestr := '0.';
count := 0;
for i := 1 to lng do begin
if str[i] = char9 then begin
if i = 3 then s9f := true;
if s9f then begin
inc(count);
ninestr := ninestr + char9;
end;
end
else s9f := false;
end;
if count > 0 then begin
nines := ninestr;
ans := x - nines;
end
else ans := x;
result := count;
end;
//------------------------------------------------------------------------------
// error function calc
// zの値が∞だとerror関数の値が1になるのですが、演算桁数の関係で
// 50桁表示でzの値が10.7程度で1になってしまうため9の数での表現を採用しています。
Procedure calc_error_function;
var
z, absz, ans, mans, ansm99, zmax, one, ansmone : bigdecimal;
nineN, dispn : integer;
str99 : string;
begin
zmax := ZINMAX;
try
z := form1.zEdit.Text;
except
on EConverterror do begin
MessageDlg('z の値に間違いがあります。', mtError, [mbOK], 0);
exit;
end;
end;
absz := z.Abs(z);
if absz > zmax then begin
MessageDlg('z の絶対値が演算の最大値より大きくなっています。', mtError, [mbOK], 0);
exit;
end;
one := bigdecimal.One;
// error 関数計算
ans := Error_function(z);
// errorC 関数計算
mans := bigdecimal.One - ans;
// zの値が1.2を超えると0.999・・9の9の値が増えるの9の値を数で表現 0. + 9の数＋0.99・9を減算した値として表示
if z >= 0 then nineN := nineNo(ans, ansm99)
else nineN := nineNo(-ans, ansm99);
dispn := 50 - nineN;
if dispn < 3 then dispn := 5;
if nineN = 0 then ansm99 := ansm99.RoundToPrecision(50)
else ansm99 := ansm99.RoundToPrecision(dispn);
if ans = '0' then form1.ansREdit.Text := '0.0'
else begin
if (nineN > 0) and (Form1.CheckBox1.Checked = false) then begin
if ansm99 = bigdecimal.Zero then str99 := '0'
else str99 := ansm99.ToString;
if z >= 0 then Form1.ansREdit.Text := '0. 9xx' + inttostr(nineN) + '個 + ' + str99
else Form1.ansREdit.Text := '-0. 9xx' + inttostr(nineN) + '個 - ' + str99;
end
else begin
ans := ans.RoundToPrecision(50);
Form1.ansREdit.Text := ans.ToString;
end;
end;
if mans > one then ansmone := mans - one
else ansmone := mans;
nineN := nineNo(ansmone, ansm99);
dispn := 50 - nineN;
if dispn < 3 then dispn := 5;
if nineN = 0 then ansm99 := ansm99.RoundToPrecision(50)
else ansm99 := ansm99.RoundToPrecision(dispn);
if (nineN > 0) and (Form1.CheckBox1.Checked = false) then begin
if ansm99 = bigdecimal.Zero then str99 := '0'
else str99 := ansm99.ToString;
if mans > one then Form1.OneMansEdit.Text := '1. 9xx' + inttostr(nineN) + '個 + ' + str99
else Form1.OneMansEdit.Text := '0. 9xx' + inttostr(nineN) + '個 + ' + str99;
end
else begin
mans := mans.RoundToPrecision(50);
form1.OneMansEdit.Text := mans.ToString;
end;
end;
//------------------------------------------------------------------------------
// 有効桁数と収束判定値のデフォルト値をセット
procedure TForm1.calcBtnClick(Sender: TObject);
begin
bigdecimal.DefaultPrecision := DPS;
calc_error_function;
end;
procedure TForm1.FormCreate(Sender: TObject);
begin
zedit.EditLabel.Caption := '|z|<=' + ZINMAX;
label1.Caption := 'Zの値が無限大の時erf(∞)=1となるのですが演算上入力の最大値は' + ZINMAX + 'です。';
nEdit.Text := 'loops ='
end;
end.
error_function.zip
三角関数、逆三角関数、その他関数 に戻る