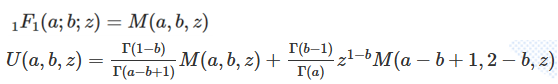
第2種合流型超幾何関数(Confluent Hypergeometric function of Second kind)
第2種合流型超幾何関数についての詳細は、インターネットで検索して下さい。
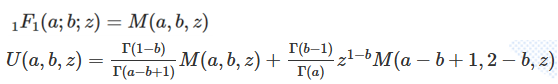
第2種合流型幾何関数は、第1種の計算が元になっているのですが、Γ関数の分数の計算があり、分子が無限大になる場合と、第1種の計算が無限大になる場合があるので、極限の計算が必要です。
極限の計算は、ガウスの超幾何関数で、微小値Δの加減で計算すれば良いことがわかっているので、此処でもその手法を使用します。
ガウスの超幾何関数に対して、cの値が無くなっているので、ガウスの超幾何関数より有効桁数は少なくΔ値は大きくしてあります。
極限計算の為の±Δの計算は、bの値が整数の時のみとなります。
計算は第1種を使用するので、第1種の計算結果も表示します、第1種には極限計算はありません。
プログラム
Bigintegr & Bigdecimal の組み込み方は第1種ケルビン関数を参照して下さい。
main.pas
// 合流型超幾何関数 unit main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Velthuis.BigIntegers, Velthuis.Bigdecimals, Vcl.StdCtrls, Vcl.ExtCtrls, Vcl.Buttons, Vcl.Imaging.pngimage, system.UITypes, complex_sub; type TForm1 = class(TForm) izEdit: TLabeledEdit; zEdit: TLabeledEdit; ibEdit: TLabeledEdit; bEdit: TLabeledEdit; iaEdit: TLabeledEdit; aEdit: TLabeledEdit; epsEdit: TLabeledEdit; PrecisionEdit: TLabeledEdit; Memo1: TMemo; CalcBtn: TBitBtn; Image1: TImage; deltEdit: TLabeledEdit; BitBtn1: TBitBtn; procedure CalcBtnClick(Sender: TObject); procedure FormCreate(Sender: TObject); procedure BitBtn1Click(Sender: TObject); private { Private 宣言 } function inputcheck(var precision: integer): boolean; public { Public 宣言 } end; var Form1: TForm1; implementation {$R *.dfm} //------------------------------------------------------------------------------ // a, b, z 因数 // eps 収束判定値 // pre 有効桁数 // ans 答え // 戻り値 正常 0 1 +∞ -1 -∞ function Confluent_Hypergeometri_of_first(aa, bb, zz: combig; eps : bigdecimal; var ans : combig): integer; var a, b, z, czero, siguma, azsbnn : combig; az, bnn : combig; ap, bp, an, bn, zn : combig; np, nn , comabs : bigdecimal; n : integer; begin result := 0; czero.r := zero; // czero czero.i := zero; a := aa; // a b := bb; // b z := zz; // z ap := a; // (a) = a bp := b; // (b) = b np := one; // (n) = 1 an := ap; // (a)n = (a); bn := bp; // (b)n = (b) nn := np; // n! = (n) zn := z; // z^n = z n := 1; siguma := czero; // Σ=0 azsbnn.r := one; azsbnn.i := zero; repeat az := cmul(an, zn); // (a)n * z^n if caeqb(az, czero) then begin // (a)n * z^n = 0 comabs := zero; // 収束値=0 break; end; if caeqb(bn, czero) then begin // (b)n = 0 az := cmul(cmul(ap, z), azsbnn); // (a)nz^n/(b)'n 'n=n-1 azsbnn=(a)'nz^'n/(b)'n if az.r >= zero then result := 1 else result := -1; break; end; bnn := cmulb(bn, nn); // (b)n * n! az := combiground(az); // precisionsに丸め bnn := combiground(bnn); // precisionsに丸め azsbnn := cdiv(az, bnn); // α = ((a)n * z^n) / ((b)n * n!) siguma := cadd(siguma, azsbnn); // Σ = Σ+ α ap.r := ap.r + one; // a=a+1 bp.r := bp.r + one; // b=b+1 np := np + one; // n=n+1 an := cmul(an, ap); // (a)n bn := cmul(bn, bp); // (b)n zn := cmul(zn, z); // z^n nn := nn * np; // n! an := combiground(an); // (a)n precisionsに丸め bn := combiground(bn); // (b)n precisionsに丸め zn := combiground(zn); // z^n precisionsに丸め nn := nn.RoundToPrecision(precisions); //n! precisionsに丸め comabs := cabs(azsbnn); // comabs = |azsbnn| inc(n); until (comabs <= eps) or (n > 10000); if result <> 0 then ans := az else ans := caddb(siguma, one); // Σ=Σ+1 comabs := comabs.RoundToPrecision(15); if result = 0 then form1.Memo1.Lines.Append('loop = ' + inttostr(n) + ' 収束値 ' + comabs.ToString); end; //------------------------------------------------------------------------------ // x <= 0 で 整数なら result = true function zeroorounderbig(xx: combig): boolean; var xc : bigdecimal; x : combig; begin // xxの値を変化させるxxの元値を解放不可になるのでコピーして使用します x := xx; result := false; if not x.i.IsZero then exit; // frac 桁落ち対策 x.r := x.r.RoundToPrecision(200); xc := x.r.Frac; if not xc.IsZero then exit;; if x.r.IsNegative or x.r.IsZero then result := true; end; //------------------------------------------------------------------------------ // aa, bb, zz 因数 // eps 収束判定値 // ans 答え // 戻り値 正常 0 // ±∞が発生しないようにbにΔ値加減算(極限計算)する必要があります。 // 発生しない場合は、Δ値加減算の必要ありません。 function Confluent_Hypergeometri_of_second_sub(aa, bb, zz: combig; eps : bigdecimal; var ans : combig): integer; var cone, ctwo, czero : combig; a, b, z, onemb, bmone, ambpone, twomb: combig; gonemb, gambpone, gbmone, ga, zhonemb: combig; g1, g2, m1, m2, fa, fb : combig; begin a := aa; b := bb; z := zz; cone.r := one; // 1+0i cone.i := zero; ctwo := cadd(cone, cone); // 2+0i czero.r := zero; // 0+0i czero.i := zero; onemb := csub(cone, b); // 1-b ambpone := cadd(csub(a, b), cone); // a-b-1 bmone := csub(b, cone); // b-1 twomb := csub(ctwo, b); // 2-b // Γ値計算 if not zeroorounderbig(ambpone) then begin // not (ambpone <= 0 整数) gammabig(onemb, gonemb); // Γ(1-b) gammabig(ambpone, gambpone); // Γ(a-b+1) gonemb := combiground(gonemb); // precisions 丸め gambpone := combiground(gambpone); // precisions 丸め g1 := cdiv(gonemb, gambpone); // Γ(1-b)/Γ(a-b+1) end else g1 := czero; // 分母が±∞ならゼロ if not zeroorounderbig(a) then begin // not (a <= 0 整数) gammabig(bmone, gbmone); // Γ(b-1) gammabig(a, ga); // Γ(a) gbmone := combiground(gbmone); // precisions 丸め ga := combiground(ga); // precisions 丸め g2 := cdiv(gbmone, ga); // Γ(b-1)/ Γ(a) end else g2 := czero; // 分母が±∞ならゼロ // M(a,b,z) 計算 result := Confluent_Hypergeometri_of_first(a, b, z, eps, m1); // M1 if result <> 0 then exit; // ±∞時エラー終了 // M(a-b+1,2-b,z) 計算 result := Confluent_Hypergeometri_of_first(ambpone, twomb, z, eps, m2); // M2 if result <> 0 then exit; // ±∞時エラー終了 // Γ(1-b)/Γ(a-b+1)*M(a,b,z) fa := cmul(g1, m1); // fa = g1 * m1 zhonemb := pow_big(z, onemb, eps); // z^(1-b) // Γ(b-1)/ Γ(a) * z^(1-b) * M(a-b+1,2-b,z) fb := cmul(cmul(g2, zhonemb), m2); // fb = g2 * z^(1-b) * M2 // Γ(1-b)/Γ(a-b+1)*M(a,b,z) + Γ(b-1)/ Γ(a) * z^(1-b) * M(a-b+1,2-b,z) ans := combiground(cadd(fa, fb)); // ans = fa + fb precisions 丸め end; // aa, bb, zz 因数 // eps 収束判定値 // ans 答え // 極限計算 b a <=0 整数時Γ/Γ計算は0になるので、bのみ±Δ極限計算 // 戻り値 0 正常 1 or -1 演算エラー function Confluent_Hypergeometri_of_second(aa, bb, zz: combig; eps : bigdecimal; var ans : combig): integer; var a, b, z : combig; cone, ctwo, bpmd : combig; ans1, ans2 : combig; rfrac : bigdecimal; fm, f1, f2 : integer; begin // ±∞が発生しないようにΔ値加減算設定(極限計算用) a := aa; b := bb; z := zz; cone.r := one; cone.i := zero; ctwo := cadd(cone, cone); // b が整数なら fm = 1 極限計算 fm := 0; rfrac := b.r.Frac; if (rfrac = zero) and (b.i = zero) then fm := 1; f2 := 0; if fm <> 0 then begin // ±Δ 計算 bpmd := caddb(b, delt); // b+Δb f1 := Confluent_Hypergeometri_of_second_sub(a, bpmd, z, eps, ans1); bpmd := csubb(b, delt); // b-Δb f2 := Confluent_Hypergeometri_of_second_sub(a, bpmd, z, eps, ans2); ans := cdiv(cadd(ans1, ans2), ctwo); // (ans(+Δ) + ans(-Δ)) / 2 end else // Δ無し f1 := Confluent_Hypergeometri_of_second_sub(a, b, z, eps, ans); result := 0; if (f1 <> 0) or (f2 <> 0) then result := $1; if fm <> 0 then result := result or $100; end; //------------------------------------------------------------------------------ // 入力値の最大値最小値のチェック function inbigcheck(s, xtext: string): boolean; const MAXSTR = '200'; MINSTR = '1e-100'; var max, min, x: bigdecimal; begin result := false; try x := xtext; except on EConverterror do begin MessageDlg(s + ' の値に間違いがあります。', mtError, [mbOK], 0); // application.MessageBox(pchar(s + ' の値に間違いがあります。'),'エラー', 0); exit; end; end; max := MAXSTR; min := MinSTR; if x.Abs(x) > max then begin application.MessageBox(pchar('abs(' + s + ')の値が大きすぎます。' + #13#10 + '±' + MAXSTR + 'が限度です。'),'注意',0); exit; end; if (x.Abs(x) < min) and (x.Abs(x) <> zero) then begin application.MessageBox(pchar('abs(' + s + ')の値が小さすぎます。' + #13#10 + '±' + MINSTR + 'が限度です。'),'注意',0); exit; end; result := true; end; // 入力チェック function TForm1.inputcheck(var precision: integer): boolean; const DMIN = '1e-100'; DMAX = '1e-10'; var chd: double; ch : integer; deltmax, deltmin : bigdecimal; begin result := false; if not inbigcheck('a 実数', aedit.Text) then exit;; if not inbigcheck('b 実数', bedit.Text) then exit;; if not inbigcheck('z 実数', zedit.Text) then exit;; if not inbigcheck('aの虚数', iaedit.Text) then exit;; if not inbigcheck('bの虚数', ibedit.Text) then exit;; if not inbigcheck('zの虚数', izedit.Text) then exit;; try delt := deltedit.Text; except on EConverterror do begin application.MessageBox(pchar('Δ の値に間違いがあります。'), nil); exit; end; end; deltmin := DMIN; deltmax := DMAX; if delt > deltmax then begin application.MessageBox('Δ値 は1e-10 より小さくして下さい。','注意',0); exit; end; if delt < deltmin then begin application.MessageBox('Δ値 は1e-100 より大きくして下さい。','注意',0); exit; end; val(precisionedit.Text, precision, ch); if ch <> 0 then begin application.MessageBox('有効桁数 の値に間違いがあります。','注意',0); exit; end; if precision < 10 then begin application.MessageBox('有効桁数 は10以上にして下さい。','注意',0); exit; end; if precision > 1000 then begin application.MessageBox('有効桁数 は1000以下にして下さい。','注意',0); exit; end; val(epsedit.Text, chd, ch); if ch <> 0 then begin application.MessageBox('収束判定値に間違いがあります。','注意',0); exit; end; if chd < 1e-100 then begin application.MessageBox('収束判定値は1e-100より大きくして下さい。','注意',0); exit; end; if chd > 1e-1 then begin application.MessageBox('収束判定値は1e-1より小さく下さい。','注意',0); exit; end; result := true; end; //------------------------------------------------------------------------------ // 数値の後ろのゼロ消去 function ZeroErase(s : string): string; const EP = 'e'; ZC = '0'; dt = '.'; var c : char; i, j, k, l : integer; begin l := length(s); // l文字長さ j := 1; // j=1初期化 for i := 1 to l do begin // 一文字目から c := s[i]; // 一文字取り出し if c = EP then begin // 'e'だったら j := i - 1; // eの前の文字No break; // ブレーク end; j := i; // 'e'がなかったらj=i end; result := ''; // ''設定 if j < l then begin // jが文字長さより小さかったら for i := l downto j + 1 do // 文字の後ろから result := s[i] + result; // 'e'迄コピー end; K := 1; // k=1初期化 for i := j downto 1 do begin // 'e'の前の文字から c := s[i]; // 一文字取り出し'0'は読み飛ばす if c <> ZC then begin // '0'で無かったら k := i; // k=i if c = DT then k := k + 1; // '.'だったら k=i+1 '.'の後の'0'は残す break; // ブレーク end; end; for i := k downto 1 do // kから1文字目までコピー result := s[i] + result; // 前に追加コピー end; //------------------------------------------------------------------------------ // 表示桁数設定 function roundNumber(rn: string): integer; const MS = '-'; var leng, i : integer; str : string; ch : char; lm, ll : double; begin str := ''; // '' leng := length(rn); // 文字長さ '1e-nn' result := 0; for i := leng downto 1 do begin // 後ろから '-'の後ろの文字取り出し ch := rn[i]; // 1文字取り出し if ch = MS then begin // '-'だったら result := strtoint(str); // 数値に変換 break; // ブレーク end; str := ch + str; // 前に文字追加 end; if result = 0 then begin // -'が無かったら lm := strtofloat(rn); // 数値に変換 im result := 0; // 1 ll := 1; // ll=1 repeat ll := ll / 10; // ll<=im まで10で除算 inc(result); // result := result + 1 until ll < lm; dec(result); // result := result - 1 end; if result > 50 then result := 50; end; // 計算 procedure TForm1.CalcBtnClick(Sender: TObject); const ZE = '1e-55'; // ゼロ判定値 var a, b, z, ans : combig; eps : bigdecimal; f1 : integer; absans, zem, tmb : bigdecimal; begin if inputcheck(precisions) = false then exit; // 入力値チェック bigdecimal.DefaultPrecision := precisions; // 有効桁数 a.r := aedit.Text; // a.re a.i := iaedit.Text; // a.im b.r := bedit.Text; // b.re b.i := ibedit.Text; // b.im z.r := zedit.Text; // z.re z.i := izedit.Text; // z/im eps := epsedit.Text; // 収束判定値 zem := ZE; // ゼロ判定値 tmb := delt / eps; // Δ/ 収束判定値 if tmb < 10 then begin application.MessageBox('収束判定値はΔ値の10分の1以下にしてください。','注意',0); end; memo1.Clear; memo1.Lines.Append('第1種合流型超幾何関数 M(a,b,z)'); f1 := Confluent_Hypergeometri_of_first(a, b, z, eps, ans); if f1 = 0 then begin ans.r := ans.r.RoundToPrecision(60); ans.i := ans.i.RoundToPrecision(60); memo1.Lines.Append(' (60桁表示)'); memo1.Lines.Append(' (' + ans.r.ToString + ')'); memo1.Lines.Append(' (' + ans.i.ToString + ' i' + ')'); absans := absans.Abs(ans.r); if absans < zem then ans.r := zero; absans := absans.Abs(ans.i); if absans < zem then ans.i := zero; ans.r := ans.r.RoundToPrecision(roundNumber(epsedit.Text)); ans.i := ans.i.RoundToPrecision(roundNumber(epsedit.Text)); memo1.Lines.Append('ans ' + intTostr(roundNumber(epsedit.Text)) + '桁に丸め'); if ans.r = zero then memo1.Lines.Append(' 0.0') else memo1.Lines.Append(ZeroErase(' ' + ans.r.ToString)); if ans.i = zero then memo1.Lines.Append(' 0.0 i') else memo1.Lines.Append(ZeroErase(' ' + ans.i.ToString) + ' i'); end else begin memo1.Lines.Append('ans'); if ans.r > zero then memo1.Lines.Append(' ∞'); if ans.r < zero then memo1.Lines.Append(' -∞'); if ans.i > zero then memo1.Lines.Append(' +∞ i'); if ans.i < zero then memo1.Lines.Append(' -∞ i'); end; memo1.Lines.Append(''); memo1.Lines.Append('第2種合流型超幾何関数 U(a,b,z)'); f1 := Confluent_Hypergeometri_of_second(a, b, z, eps, ans); // 第2種合流型超幾何関数は必ず収束するので±∞は発生しません、念の為。 if f1 and $1 <> 0 then begin memo1.Lines.Append('±∞ 演算エラー'); exit; end; ans.r := ans.r.RoundToPrecision(60); ans.i := ans.i.RoundToPrecision(60); memo1.Lines.Append(' (60桁表示)'); memo1.Lines.Append(' (' + ans.r.ToString + ')'); memo1.Lines.Append(' (' + ans.i.ToString + ' i' + ')'); if f1 and $100 = 0 then memo1.Lines.Append('ans ' + intTostr(roundNumber(epsedit.Text)) + '桁に丸め') else memo1.Lines.Append('ans ' + intTostr(roundNumber(epsedit.Text)) + '桁に丸め 極限値計算 '); ans.r := ans.r.RoundToPrecision(roundNumber(epsedit.Text)); ans.i := ans.i.RoundToPrecision(roundNumber(epsedit.Text)); absans := absans.Abs(ans.r); if absans < zem then ans.r := zero; absans := absans.Abs(ans.i); if absans < zem then ans.i := zero; if ans.r = zero then memo1.Lines.Append(' 0.0') else memo1.Lines.Append(ZeroErase(' ' + ans.r.ToString)); // 最後の行は改行しない if ans.i = zero then memo1.Text := memo1.Text + ' 0.0 i' else memo1.Text := memo1.Text + ZeroErase(' ' + ans.i.ToString) + ' i '; end; //------------------------------------------------------------------------------ // デフォルト値に設定 procedure TForm1.BitBtn1Click(Sender: TObject); begin deltedit.Text := DELTB; epsedit.Text := EPS; end; //------------------------------------------------------------------------------ // 初期設定 procedure TForm1.FormCreate(Sender: TObject); begin precisionedit.Text := intTostr(DPS); deltedit.Text := DELTB; memo1.Clear; end; end.
complex_sub.pas
unit complex_sub; interface uses Velthuis.BigIntegers, Velthuis.Bigdecimals; type combig = record // 複素数構造体 r : bigdecimal; i : bigdecimal; end; var zero, one : bigdecimal; // 0, 1 precisions : integer; // 有効桁数 paib : bigdecimal; // π maxmpfbig : Bigdecimal; // Γ(0)値 ]:∞の代用 delt : bigdecimal; // 極限値用Δ log_2pis2 : combig; // Ln(2π)/2 ctwo, cone : combig; // 2+0i, 1+0i const DPS = 200; // 除算時有効桁数 NB = 120; // ベルヌーイ数 配列数 NB + 1 EPSC = '1e-100'; // log_big 収束反対値 ln(x) EPS = '1e-60'; // 合流型超幾何関数収束判定値 DELTB = '1e-30'; // 極限値Δ function combiground(x : combig): combig; function cadd(a, b: comBig): ComBig; function csub(a, b: ComBig): ComBig; function caddb(a: combig; b:bigdecimal): combig; function csubb(a : combig; b: bigdecimal): combig; function cmulb(a: Combig; b: bigdecimal): ComBig; function cmul(a, b: Combig): ComBig; function cdivb(a: Combig; b: bigdecimal): Combig; function cdiv(a, b: Combig): Combig; function caeqb(x, y : combig): boolean; function cabs(a : combig): bigdecimal; function gammabig(xx : combig; var ans: combig) : integer; function pow_big(x, y : combig; eps : bigdecimal): combig; function pi_big: Bigdecimal; function log_big(z : combig; eps : bigdecimal; dpcs: integer): combig; implementation //------------------------------ comprex calc------------------------------------------- var z10 : combig; Z10F : boolean = false; BM : array[0..NB] of Bigdecimal; // ベルヌーイ数配列 tmpb: combig; epsb : bigdecimal; // x: combig dpcs桁に丸め function combiground(x : combig): combig; begin result.r := x.r.RoundToPrecision(precisions); result.i := x.i.RoundToPrecision(precisions); end; // ComBig複素数の加算 function cadd(a, b: comBig): ComBig; begin result.r := a.r + b.r; result.i := a.i + b.i; end; // ComBig複素数の減算 function csub(a, b: ComBig): ComBig; begin result.r := a.r - b.r; result.i := a.i - b.i; end; // combig + bigdecimal function caddb(a: combig; b:bigdecimal): combig; begin result.r := a.r + b; result.i := a.i; end; // combig - bigdecimal function csubb(a : combig; b: bigdecimal): combig; begin result.r := a.r - b; result.i := a.i; end; // Combig bigdecimalの乗算 function cmulb(a: Combig; b: bigdecimal): ComBig; begin result.r := a.r * b; result.i := a.i * b; end; // Combig複素数の乗算 function cmul(a, b: Combig): ComBig; begin result.r := a.r * b.r - a.i * b.i; result.i := a.r * b.i + a.i * b.r; result := combiground(result); end; // Combig bigdecimalの除算 function cdivb(a: Combig; b: bigdecimal): Combig; begin if b <> Bigdecimal.Zero then begin result.r := a.r / b; result.i := a.i / b; end else begin result.r := Bigdecimal.Zero; result.i := Bigdecimal.Zero; end; end; // Combig複素数の除算 function cdiv(a, b: Combig): Combig; var bb, arbraibi, aibrarbi: Bigdecimal; begin bb := b.r * b.r + b.i * b.i; arbraibi := a.r * b.r + a.i * b.i; aibrarbi := a.i * b.r - a.r * b.i; bb := bb.RoundToPrecision(precisions); arbraibi := arbraibi.RoundToPrecision(precisions); aibrarbi := aibrarbi.RoundToPrecision(precisions); if bb <> Bigdecimal.Zero then begin result.r := arbraibi / bb; result.i := aibrarbi / bb; end else begin result.r := Bigdecimal.Zero; result.i := Bigdecimal.Zero; end; end; // a:combig = b:combig function caeqb(x, y : combig): boolean; begin if (x.r = y.r) and (x.i = y.i) then result := true else result := false; end; // Combigの絶対値 function cabs(a : combig): bigdecimal; var arh2, aih2 : bigdecimal; tmp : bigdecimal; begin arh2 := a.r * a.r; aih2 := a.i * a.i; arh2 := arh2.RoundToPrecision(precisions); aih2 := aih2.RoundToPrecision(precisions); tmp := arh2 + aih2; result := bigdecimal.Sqrt(tmp, precisions); end; //------------------------------------------------------------------------------ // 最大公約数 ユークリッドの互除法 BigInteger function gcd_BigInteger(x, y: BigInteger): BigInteger; var t : BigInteger; begin while y <> 0 do begin t := x mod y; x := y; y := t; end; result := x; end; // π // https://www.kurims.kyoto-u.ac.jp/~ooura/pi_fft-j.html // T.Ooura AGM アルゴリズ function pi_big: Bigdecimal; var n, dpcs : integer; rmback : BigDecimal.RoundingMode; SQRT_SQRT_EPSILON, c, b, e : BigDecimal; npow : Bigdecimal; a, one, two, four, five, eight : Bigdecimal; begin rmBack := BigDecimal.DefaultRoundingMode; // 除算丸めモードバックアップ dpcs := precisions + 5; // 指定精度 + α BigDecimal.DefaultPrecision := dpcs; BigDecimal.DefaultRoundingMode := rmNearesteven; one := '1'; one := one.RoundToPrecision(dpcs); // oneの有効桁数をdpcsに設定 two := '2'; four := '4'; five := '5'; eight := '8'; SQRT_SQRT_EPSILON := one / BigDecimal.IntPower(two, dpcs shl 0); // 収束判定値 c := BigDecimal.Sqrt(one / eight, dpcs * 2); a := one + c + c + c; b := BigDecimal.Sqrt(a, dpcs * 2); e := b - five / eight; b := b + b; c := e - c; a := a + e; npow := '4'; n := 0; while (e > SQRT_SQRT_EPSILON) and (n < 100) do begin npow := npow + npow; // 8,16,32,64 e := (a + b) / two; // 平均値 除算有効桁数での丸め b := a * b; b := b.RoundToPrecision(dpcs); // pcs + α 丸め b := BigDecimal.Sqrt(b, dpcs * 2); // 平方根有効桁数での丸め e := e - b; b := b + b; c := c - e; a := e + b; inc(n); end; e := e * e; e := e.RoundToPrecision(dpcs); // pcs + α 丸め e := e / four; // e = e * e / 4 a := a + b; result := (a * a - e - e / two) / (a * c - e) / npow; // 除算の順番に注意 result := result.RoundToPrecision(precisions); // 指定の精度に丸め BigDecimal.DefaultPrecision := precisions; // 除算演算精度復帰 BigDecimal.DefaultRoundingMode := rmBack; // 除算丸めモード復帰 end; // ベルヌーイ数 // Akiyama-Tanigawa algorithm // BigInteger procedure Bernoulli_number_BigInteger; const n = (NB + 1) * 2; var m, j, k, dpcs: integer; a : array of BigInteger; // 分子 b : array of BigInteger; // 分母 tmpN : BigInteger; // 分子 tmpD : BigInteger; // 分母 gcd : BigInteger; // 最大公約数 b0 : BigInteger; ad, bd : bigdecimal; begin setlength(a, n + 1); setlength(b, n + 1); dpcs := BigDecimal.DefaultPrecision; k := 0; for m := 0 to n do begin a[m] := 1; // 分子 初期値 b[m] := (m + 1); // 分母 初期値 for j := m - 1 downto 0 do begin tmpN := a[j] * b[j + 1] - a[j + 1] * b[j]; // 分子 tmpN := tmpN * (j + 1); // 〃 tmpD := b[j] * b[j + 1]; // 分母 gcd := gcd_BigInteger(tmpN, tmpD); // 最大公約数 a[j] := tmpN div gcd; b[j] := tmpD div gcd; end; ad := a[0]; ad := ad.RoundToPrecision(dpcs); // dpcs桁に丸め if (m > 0) and (m mod 2 = 0) then begin b0 := b[0]; // logΓ関数用に分母値Bの値計算 b0 := b0 * m * (m -1); // m ベルヌーイ数No bd := b0; bd := bd.RoundToPrecision(dpcs); // dpcs桁に丸め BM[k] := ad / bd; inc(k); end; end; end; // z 入力値 複素数 // eps 収束判定値 // dpcs 有効桁数 // ndis 収束表示 true 表示 false 非表示 function log_big_sub(z : Combig; eps : bigdecimal; dpcs: integer; ndis: boolean): Combig; const NN = 1000000; var s, x, zm1, zp1, xh2, xg, n2p1 : ComBig; one, two : Combig; xgsn : Combig; asabs : bigdecimal; n : integer; begin one.r := Bigdecimal.One; // 1 one.i := Bigdecimal.Zero; // two := cadd(one, one); // 2 zm1 := csub(z, one); // z - 1 zp1 := cadd(z, one); // z + 1 x := cdiv(zm1, zp1); // x = (z-1)/(z+1) s.r := Bigdecimal.Zero; s.i := Bigdecimal.Zero; xh2 := cmul(x, x); // x^2 xg := x; // n = 0; x^(2n+1) n2p1 := one; // 2n+1 = 1 n := 0; repeat xg.r := xg.r.RoundToPrecision(dpcs); xg.i := xg.i.RoundToPrecision(dpcs); xgsn := cdiv(xg, n2p1); // x^(2n+1) / (2n+1) s := cadd(s, xgsn); // Σ xg := cmul(xg, xh2); // x^(2n+1) n2p1 := cadd(n2p1, two); // 2n + 1 inc(n); asabs := cabs(xgsn); until (asabs < eps) or (n > NN); s := cmul(s, two); result := s; end; // z 因数 // eps 収束判定値 // dpcs 有効桁数 // 返り値 対数複素数 function log_big(z : combig; eps : bigdecimal; dpcs: integer): combig; var zb : combig; z10n : combig; Zmax, ten, one, bn : bigdecimal; pi_big2: bigdecimal; begin if (z.r = bigdecimal.Zero) and (z.i = bigdecimal.Zero) then begin result.r := bigdecimal.Zero; result.i := bigdecimal.Zero; exit; end; pi_big2 := paib / bigdecimal.Two; // paib = pi_bigs zb := z; // 虚数と実数両方ともゼロでないなら 実数部側を大きな値にして演算誤差を小さくします if (zb.r <> bigdecimal.Zero) and (zb.i <> bigdecimal.Zero) then begin if zb.i.Abs(zb.i) > zb.r.Abs(zb.r) then begin // 虚数の絶対値が実数の絶対値より大きい時入れ替え z.r := zb.i; z.i := zb.r; if zb.i < bigdecimal.Zero then begin // 虚数が負数だったら符号反転 z.r := -z.r; z.i := -z.i; end; end else begin // 虚数の絶対値が実数の絶対値と等しいか小さい時 if zb.r < bigdecimal.Zero then begin // 実数の値が負数だったら符号反転 z.r := -zb.r; z.i := -zb.i; end; end; end; // z.rが0でz.iがゼロでない時 虚数部と実数部入れ替え if (zb.r = bigdecimal.Zero) and (zb.i <> bigdecimal.Zero) then begin z.r := zb.i; z.i := zb.r; if z.r < bigdecimal.Zero then z.r := -z.r; // 実数部が負数だったら符号反転 虚数部ゼロなのでそのまま end; // 実数部が負数ので虚数部ゼロの時符号を反転 虚数部ゼロなのでそのまま if (zb.r <> bigdecimal.Zero) and (zb.i = bigdecimal.Zero) then if zb.r < bigdecimal.Zero then z.r := -zb.r; // 10の対数を利用して大きな値の計算を速くします ten := '10'; ten := ten.RoundToPrecision(dpcs); // dpcs桁合わせ one := bigdecimal.One; bn := bigdecimal.Zero; if not Z10F then begin z10.r := ten; // z10 : cbig Z!0F : boolean main.pas z10.i := bigdecimal.Zero; z10 := log_big_sub(z10, eps, dpcs, false); // 10の対数 Z10F := true; end; zmax := cabs(z); // zの絶対値 zmax := zmax.RoundToPrecision(dpcs); // dpcs桁合わせ z.r := z.r.RoundToPrecision(dpcs); // dpcs桁合わせ z.i := z.i.RoundToPrecision(dpcs); // dpcs桁合わせ // 10で除算又は乗算して値がの値が1~10の範囲に入るようにします。 repeat if zmax > ten then begin // zmaxが10より大きい時10で除算 z.r := z.r / ten; z.i := z.i / ten; zmax := zmax / ten; bn := bn + one; // 10で除算した回数 +になります。 end; if zmax < one then begin // zmaxが1より小さい時10を乗算 z.r := z.r * ten; z.i := z.i * ten; zmax := zmax * ten; bn := bn - one; // 10を乗算した回数 -になります。 end; until (zmax <= ten) and (zmax >= one); //---------------------------------------- // 修正された値で対数計算 result := log_big_sub(z, eps, dpcs, true); // 10の対数補正 z10n.r := z10.r * bn; // 加算する対数値計算10の対数値のn倍 z10n.i := z10.i * bn; result.r := result.r + z10n.r; // 10の対数値のn倍加算 result.i := result.i + z10n.i; //---------------------------------------- // z.rがゼロでz.iがゼロでない時 虚数部π/2補正 if (zb.r = bigdecimal.Zero) and (zb.i <> bigdecimal.Zero) then begin if zb.i >= bigdecimal.Zero then result.i := result.i + pi_big2 else result.i := result.i - pi_big2; end; // z.rの値が負数のきと符号を変更して計算しているの虚数部π補正。 if (zb.r < bigdecimal.Zero) and (zb.i = bigdecimal.Zero) then result.i := result.i + pi_big; // 虚数と実数両方ともゼロでない時 if (zb.r <> bigdecimal.Zero) and (zb.i <> bigdecimal.Zero) then begin // 次数部絶対値より虚数部の絶対値が大きい場合 if zb.i.Abs(zb.i) > zb.r.Abs(zb.r) then begin if zb.i > bigdecimal.Zero then result.i := -result.i + pi_big2 // π/2補正 else result.i := -result.i - pi_big2; end // 実数部が負数の時 else begin if zb.r < bigdecimal.Zero then if zb.i > bigdecimal.Zero then result.i := result.i + pi_big // π補正 else result.i := result.i - pi_big end; end; end; // ログガンマ多倍長 procedure log_GammaMul(x: combig; var ans : combig); var xx, v, w : combig; tmp, tmp0, s, cans : combig; i: integer; begin xx := x; // x->xx コピーして使用 v := cone; // 1 + 0i tmp.i := bigdecimal.Zero; // 0 + 0i tmp.r := NB; // NB + 0i while xx.r < tmp.r do begin v := cmul(v, xx); // v = v * x // 繰り返し計算による桁憎防止 v := combiground(v); xx := cadd(xx, cone); // x := x + 1 end; tmp := cmul(xx, xx); // x^2 w := cdiv(cone, tmp); // w = 1 / x^2 s := combiground(s); tmp.i := bigdecimal.Zero; for i := NB downto 1 do begin tmp.r := s.r + BM[i]; // tmp = s + B[i] tmp.i := s.i; s := cmul(tmp, w); // s = tmp * w // 繰り返し計算による桁憎防止 s := combiground(s); end; tmp.r := s.r + BM[0]; // tmp = s + B[0] tmp.i := s.i; s := cdiv(tmp, xx); // s = (s + B[0]) / x s := cadd(s, log_2pis2); // s = s + ln(2π)/2 tmp := log_big(v, epsb, Precisions); // ln(v) s := csub(s, tmp); // s := s - ln(v) s := csub(s, xx); // s := s - x tmp := cdiv(cone, ctwo); // tmp = 1/2 tmp0 := csub(xx, tmp); // tmp0 = x - 1/2 tmp := log_big(xx, epsb, Precisions); // ln(x) tmp0 := cmul(tmp0, tmp); // tmp0 = (x - 1/2) * ln(x) cans := cadd(s, tmp0); // ans = s + (x - 1/2) * ln(x) // 解答桁合わせ cans := combiground(cans); ans := cans; end; // sin(z) // eps 収束判定値 // dpcs 有効桁数 // 返り値 sin複素数 function sin_big(z : Combig; eps : bigdecimal; dpcs: integer): Combig; var zh2n1, zh2: combig; fa2n1, fn, one : bigdecimal; s, sb, tmp : combig; abss: bigdecimal; FG : boolean; begin // n = 0 one := bigdecimal.One; zh2n1 := z; // z^(2n+1) zh2 := cmul(z,z); // z^2 fa2n1 := one; // (2n+1)! fn := one; // (2*0+1)! s := z; // z FG := false; // 次は奇数 // n = 1 ~ repeat sb := s; zh2n1 := cmul(zh2n1, zh2); // z^(2n+1) = z^(2n+1) * Z^2 fn := fn + one; // fn = fn + 1 fa2n1 := fa2n1* fn; // (2n+1)! = fa2n1*fn fn := fn + one; // fn = fn + 1 fa2n1 := fa2n1* fn; // (2n+1)! = fa2n1*fn // 除算前に桁揃え fa2n1 := fa2n1.RoundToPrecision(dpcs); zh2n1.r := zh2n1.r.RoundToPrecision(dpcs); zh2n1.i := zh2n1.i.RoundToPrecision(dpcs); tmp := cdivb(zh2n1, fa2n1); // z^(2n+1) / (2n+1)! if FG then begin // 偶数なら s := cadd(s, tmp); // 加算 FG := false; // 次は奇数 end else begin // 奇数なら s := csub(s, tmp); // 減算 FG := true; // 次は偶数 end; abss := cabs(tmp); // |tmp| until abss < eps; result := s; end; // exp(x) テイラー級数 // x 入力値 複素数 // dpcs 有効桁数 // eps 収束判定値 // x / 8 -> ans^8 8で除算後 級数計算 最後に8乗 function exp_big(x: Combig; dpcs: integer; eps : bigdecimal): Combig; var xh, s, si: Combig; one, ass, eight, i, ih : bigdecimal; begin one := bigdecimal.One; eight := bigdecimal.Ten - bigdecimal.Two; eight := eight.RoundToPrecision(dpcs); x.r := x.r.RoundToPrecision(dpcs); x.i := x.i.RoundToPrecision(dpcs); x := cdivb(x, eight); // x/8 i := one; ih := i; xh := x; s := x; repeat i := i + one; ih := ih * i; // i! xh := cmul(xh, x); // x^n xh.r := xh.r.RoundToPrecision(dpcs); xh.i := xh.i.RoundToPrecision(dpcs); si := cdivb(xh, ih); // x^n/i! s := cadd(s, si); ass := cabs(si); until (ass < eps); s.r := s.r + one; s := cmul(s, s); // x^2 s := cmul(s, s); // x^4 result := cmul(s, s); // x^8 result.r := result.r.RoundToPrecision(dpcs); result.i := result.i.RoundToPrecision(dpcs); end; // 多倍長ガンマ 複素数 // xの値が 0 と負整数の時Γは∞になるので∞フラグセット値は1を返します。 function gammabig(xx : combig; var ans: combig) : integer; var tmp, sinx, logG, cpai : combig; x : combig; czero, cans : combig; btwo, eps : bigdecimal; begin czero.r := bigdecimal.Zero; czero.i := bigdecimal.Zero; btwo := bigdecimal.Two; eps := '1e-200'; // xxの値を変化させるxxの元値を解放不可になるのでコピーして使用します x := xx; // 虚数部がゼロで実数部がゼロを含み負の整数だったら∞ if (x.i = czero.i) and (x.r <= czero.r) then begin tmp.r := x.r.Frac; // 実数部の小数点以下取り出し if tmp.r = czero.r then begin // 小数点以下がゼロだったら ans.r := maxmpfbig; tmp.r := x.r / btwo; tmp.r := tmp.r.Frac; if tmp.r <> czero.r then ans.r := -ans.r; // 奇数だったら符号反転 ans.i := czero.i; result := 1; // ∞フラグセット exit; // 終了 end; end; cpai.r := paib; cpai.i := czero.i; // π+ 0i // 除算時用桁合わせ cpai := combiground(cpai); if x.r < czero.r then begin // x.real < 0 tmp := cmul(x, cpai); // x*π tmp := combiground(tmp); sinx := sin_big(tmp, eps, Precisions); // sin(πx); tmp := csub(cone, x); // 1-x log_GammaMul(tmp, LogG); // loggamma(1-x); logG := exp_big(logG, Precisions, eps); // exp(loggamma) cpai := combiground(cpai); sinx := combiground(sinx); tmp := cdiv(cpai, sinx); // π/sin(πx) logG := combiground(logG); tmp := combiground(tmp); cans := cdiv(tmp, logG); end else begin // x.real >= 0 log_GammaMul(x, logG); // logGamma(x) cans := exp_big(logG, Precisions, eps); // exp(loggamma) end; ans := combiground(cans); result := 0; // 成功フラグ値 end; // x^y // exp[ln(x) * y] // 実数、虚数部がゼロになる条件でも、演算誤差により、ゼロにならないのて、条件判定をして強制的 // にゼロにしています。 function pow_big(x, y : combig; eps : bigdecimal): combig; var dpcs : integer; harf, absi, absy, four : bigdecimal; lnx, tmp : combig; begin if (x.r = bigdecimal.zero) and (x.i = bigdecimal.zero) then begin result.r := bigdecimal.Zero; result.i := bigdecimal.Zero; exit; end; dpcs := BigDecimal.DefaultPrecision; lnx := log_big(x, eps, dpcs); // ln(x) lnx := combiground(lnx); // ppcs 丸め y := combiground(y); // ppcs 丸め tmp := cmul(lnx, y); tmp := combiground(tmp); // ln(x) * y result := exp_big(tmp, dpcs, eps); // xの虚数部とyの虚数部0なら if (x.i = bigdecimal.zero) and (y.i = bigdecimal.Zero) then begin harf := bigdecimal.One / bigdecimal.Two; // 0.5 absy := y.r.Abs(y.r); // yの実数部の絶対値 absi := absy.Frac; // yの実数部の絶対値の小数部 absi := absi - harf; // yの実数部の絶対値の小数部と0.5の差分 // 差分がゼロ(yの実数部の小数部が0.5) if absi = bigdecimal.Zero then // xの実数部が0と等しいか0より大きいなら if x.r >= bigdecimal.zero then result.i := bigdecimal.zero // 答えの虚数部0 // 0より小さいなら else result.r := bigdecimal.zero; // 答えの実数部0 absi := y.r.Frac; // 乗数の小数部 if absi = bigdecimal.Zero then result.i := bigdecimal.Zero; // 整数なら答えの虚数部0 end; // xの整数部とyの虚数部が0なら if (x.r = bigdecimal.Zero) and (y.i = bigdecimal.Zero) then begin absi := y.r.Frac; // 乗数の小数部 if absi = bigdecimal.Zero then begin // 整数なら absy := y.r / bigdecimal.Two; // 偶数奇数確認 absi := absy.Frac; // 小数部 if absi = bigdecimal.Zero then result.i := bigdecimal.Zero // 偶数なら虚数部0 else result.r := bigdecimal.Zero; // 奇数なら実数部0 end; end; absy := x.r.Abs(x.r); // |x.r| absi := x.i.Abs(x.i); // |x.i| // xの実数部と虚数部の絶対値が等しくてy.rがゼロでなかったら if (absy = absi) and (y.i = bigdecimal.Zero) and not (y.r = bigdecimal.Zero) then begin absi := y.r.Frac; // 乗数の小数部 if absi = bigdecimal.Zero then begin // 整数なら absy := y.r / bigdecimal.Two; // 偶数奇数確認 absi := absy.Frac; // 小数部 if absi = bigdecimal.Zero then begin // 偶数なら four := bigdecimal.Two + bigdecimal.Two; // 4 absy := y.r / four; // 4偶数奇数確認 absi := absy.Frac; // 小数部 if absi = bigdecimal.Zero then result.i := bigdecimal.Zero // 偶数なら 虚数部0 y= 4 8 else result.r := bigdecimal.Zero; // 奇数なら 虚数部0 y= 2 6 10 end; end; end; end; // 初期値設定 initialization precisions := DPS; BigDecimal.DefaultPrecision := precisions; zero := bigdecimal.Zero; one := bigdecimal.One; cone.r := bigdecimal.One; cone.i := bigdecimal.Zero; // 1 + 0i ctwo.r := bigdecimal.Two; ctwo.i := bigdecimal.Zero; // 2 + 0i paib := pi_big; // π maxmpfbig := '1.0e+1000000'; // 有効桁数 演算最大値 ガンマ計算時最大値 epsb := EPSC; tmpb.r := paib + paib; // 2π tmpb.i := bigdecimal.Zero;; log_2pis2 := log_big(tmpb, epsb, DPS); // Ln(2π) // 除算前桁合わせ log_2pis2.r := log_2pis2.r.RoundToPrecision(DPS); // dpcs桁に丸め log_2pis2.i := log_2pis2.i.RoundToPrecision(DPS); // dpcs桁に丸め log_2pis2 := cdiv(log_2pis2, ctwo); // Ln(2π)/2 Bernoulli_number_BigInteger; // ベルヌーイ数配列作成 end.
![]() Confluent_Hypergeometric_function_of_second.zip
Confluent_Hypergeometric_function_of_second.zip
三角関数、逆三角関数、その他関数 に戻る