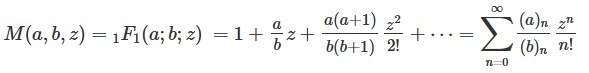
M(b,b;z) = ez
2025-03-25
b=0 時 答え∞が表示されないのを修正しました。
第1種合流型超幾何関数(Confluent Hypergeometric function of first)(クンマー関数)
第1種合流型超幾何関数についての詳細は、インターネットで検索して下さい。
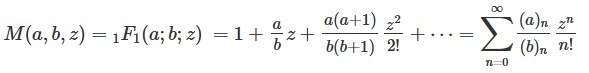
M(b,b;z) = ez
ガウスの超幾何関数と違って、bの値が0或いは負の整数のとき±∞になる以外は、必ず収束します。
分母の階乗係数の方(n!)が多いのでzの値に関わらず収束します。
プログラム
Bigintegr & Bigdecimal の組み込み方は第1種ケルビン関数を参照して下さい。
unit main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Velthuis.BigIntegers, Velthuis.Bigdecimals,
Vcl.StdCtrls, Vcl.ExtCtrls, Vcl.Buttons, Vcl.Imaging.pngimage;
type
TForm1 = class(TForm)
izEdit: TLabeledEdit;
zEdit: TLabeledEdit;
ibEdit: TLabeledEdit;
bEdit: TLabeledEdit;
iaEdit: TLabeledEdit;
aEdit: TLabeledEdit;
epsEdit: TLabeledEdit;
PrecisionEdit: TLabeledEdit;
Memo1: TMemo;
CalcBtn: TBitBtn;
procedure CalcBtnClick(Sender: TObject);
private
{ Private 宣言 }
function inputcheck(var precision: integer): boolean;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
type
combig = record
r : bigdecimal;
i : bigdecimal;
end;
var
zero, one : bigdecimal; // 0, 1
precisions : integer; // 有効桁数
//------------------------------ comprex calc-------------------------------------------
// x: combig dpcs桁に丸め
function combiground(x : combig): combig;
begin
result.r := x.r.RoundToPrecision(precisions);
result.i := x.i.RoundToPrecision(precisions);
end;
// ComBig複素数の加算
function cadd(a, b: comBig): ComBig;
begin
result.r := a.r + b.r;
result.i := a.i + b.i;
end;
{
// ComBig複素数の減算
function csub(a, b: ComBig): ComBig;
begin
result.r := a.r - b.r;
result.i := a.i - b.i;
end;
}
// combig + bigdecimal
function caddb(a: combig; b:bigdecimal): combig;
begin
result.r := a.r + b;
result.i := a.i;
end;
{
// combig - bigdecimal
function csubb(a : combig; b: bigdecimal): combig;
begin
result.r := a.r - b;
result.i := a.i;
end;
}
// Combig bigdecimalの乗算
function cmulb(a: Combig; b: bigdecimal): ComBig;
begin
result.r := a.r * b;
result.i := a.i * b;
end;
// Combig複素数の乗算
function cmul(a, b: Combig): ComBig;
begin
result.r := a.r * b.r - a.i * b.i;
result.i := a.r * b.i + a.i * b.r;
result := combiground(result);
end;
{
// Combig bigdecimalの除算
function cdivb(a: Combig; b: bigdecimal): Combig;
begin
if b <> Bigdecimal.Zero then begin
result.r := a.r / b;
result.i := a.i / b;
end
else begin
result.r := Bigdecimal.Zero;
result.i := Bigdecimal.Zero;
end;
end;
}
// Combig複素数の除算
function cdiv(a, b: Combig): Combig;
var
bb, arbraibi, aibrarbi: Bigdecimal;
begin
bb := b.r * b.r + b.i * b.i;
arbraibi := a.r * b.r + a.i * b.i;
aibrarbi := a.i * b.r - a.r * b.i;
bb := bb.RoundToPrecision(precisions);
arbraibi := arbraibi.RoundToPrecision(precisions);
aibrarbi := aibrarbi.RoundToPrecision(precisions);
if bb <> Bigdecimal.Zero then begin
result.r := arbraibi / bb;
result.i := aibrarbi / bb;
end
else begin
result.r := Bigdecimal.Zero;
result.i := Bigdecimal.Zero;
end;
end;
// a:combig = b:combig
function caeqb(x, y : combig): boolean;
begin
if (x.r = y.r) and (x.i = y.i) then result := true
else result := false;
end;
// Combigの絶対値
function cabs(a : combig): bigdecimal;
var
arh2, aih2 : bigdecimal;
tmp : bigdecimal;
begin
arh2 := a.r * a.r;
aih2 := a.i * a.i;
arh2 := arh2.RoundToPrecision(precisions);
aih2 := aih2.RoundToPrecision(precisions);
tmp := arh2 + aih2;
result := bigdecimal.Sqrt(tmp, precisions);
end;
//------------------------------------------------------------------------------
// a, b, z 因数
// eps 収束判定値
// pre 有効桁数
// ans 答え
// 戻り値 正常 0 1 +∞ -1 -∞
function Confluent_Hypergeometri_of_first(aa, bb, zz: combig; eps : bigdecimal; var ans : combig): integer;
var
a, b, z, czero, siguma, azsbnn : combig;
az, bnn : combig;
ap, bp, an, bn, zn : combig;
np, nn , comabs : bigdecimal;
n : integer;
begin
result := 0;
czero.r := zero; // czero
czero.i := zero;
a := aa; // a
b := bb; // b
z := zz; // z
ap := a; // (a) = a
bp := b; // (b) = b
np := one; // (n) = 1
an := ap; // (a)n = (a);
bn := bp; // (b)n = (b)
nn := np; // n! = (n)
zn := z; // z^n = z
n := 1;
siguma := czero; // Σ=0
azsbnn.r := one;
azsbnn.i := zero;
repeat
az := cmul(an, zn); // (a)n * z^n
if caeqb(az, czero) then begin // (a)n * z^n = 0
break;
end;
if caeqb(bn, czero) then begin // (b)n = 0
az := cmul(cmul(ap, z), azsbnn);
if az.r >= zero then result := 1
else result := -1;
break;
end;
bnn := cmulb(bn, nn); // (b)n * n!
az := combiground(az); // precisionsに丸め
bnn := combiground(bnn); // precisionsに丸め
azsbnn := cdiv(az, bnn); // α = ((a)n * z^n) / ((b)n * n!)
siguma := cadd(siguma, azsbnn); // Σ = Σ+ α
ap.r := ap.r + one; // a=a+1
bp.r := bp.r + one; // b=b+1
np := np + one; // n=n+1
an := cmul(an, ap); // (a)n
bn := cmul(bn, bp); // (b)n
zn := cmul(zn, z); // z^n
nn := nn * np; // n!
an := combiground(an); // (a)n precisionsに丸め
bn := combiground(bn); // (b)n precisionsに丸め
zn := combiground(zn); // z^n precisionsに丸め
nn := nn.RoundToPrecision(precisions); //n! precisionsに丸め
comabs := cabs(azsbnn); // comabs = |azsbnn|
inc(n);
until (comabs <= eps) or (n > 10000);
if result <> 0 then
ans := az
else
ans := caddb(siguma, one); // Σ + 1
form1.Memo1.Lines.Append('loop = ' + inttostr(n));
end;
//------------------------------------------------------------------------------
// 入力値の最大値最小値のチェック
function inbigcheck(s, xtext: string): boolean;
const
MAXSTR = '200';
MINSTR = '1e-100';
var
max, min, x: bigdecimal;
begin
result := false;
try
x := xtext;
except
on EConverterror do begin
application.MessageBox(pchar(s + ' の値に間違いがあります。'), nil);
exit;
end;
end;
max := MAXSTR;
min := MinSTR;
if x.Abs(x) > max then begin
application.MessageBox(pchar('abs(' + s + ')の値が大きすぎます。' + #13#10 +
'±' + MAXSTR + 'が限度です。'),'注意',0);
exit;
end;
if (x.Abs(x) < min) and (x.Abs(x) <> zero) then begin
application.MessageBox(pchar('abs(' + s + ')の値が小さすぎます。' + #13#10 +
'±' + MINSTR + 'が限度です。'),'注意',0);
exit;
end;
result := true;
end;
// 入力チェック
function TForm1.inputcheck(var precision: integer): boolean;
var
chd: double;
ch : integer;
begin
result := false;
if not inbigcheck('a 実数', aedit.Text) then exit;;
if not inbigcheck('b 実数', bedit.Text) then exit;;
if not inbigcheck('z 実数', zedit.Text) then exit;;
if not inbigcheck('aの虚数', iaedit.Text) then exit;;
if not inbigcheck('bの虚数', ibedit.Text) then exit;;
if not inbigcheck('zの虚数', izedit.Text) then exit;;
val(precisionedit.Text, precision, ch);
if ch <> 0 then begin
application.MessageBox('有効桁数 の値に間違いがあります。','注意',0);
exit;
end;
if precision < 10 then begin
application.MessageBox('有効桁数 は10以上にして下さい。','注意',0);
exit;
end;
if precision > 1000 then begin
application.MessageBox('有効桁数 は1000以下にして下さい。','注意',0);
exit;
end;
val(epsedit.Text, chd, ch);
if ch <> 0 then begin
application.MessageBox('収束判定値に間違いがあります。','注意',0);
exit;
end;
if chd < 1e-100 then begin
application.MessageBox('収束判定値は1e-100より大きくして下さい。','注意',0);
exit;
end;
if chd > 1e-1 then begin
application.MessageBox('収束判定値は1e-1より小さく下さい。','注意',0);
exit;
end;
result := true;
end;
//------------------------------------------------------------------------------
// 数値の後ろのゼロ消去
function ZeroErase(s : string): string;
const
EP = 'e';
ZC = '0';
dt = '.';
var
c : char;
i, j, k, l : integer;
begin
l := length(s);
j := 1;
for i := 1 to l do begin
c := s[i];
if c = EP then begin
j := i - 1;
break;
end;
j := i;
end;
result := '';
if j < l then begin
for i := l downto j + 1 do
result := s[i] + result;
end;
K := 1;
for i := j downto 1 do begin
c := s[i];
if c <> ZC then begin
k := i;
if c = DT then k := k + 1;
break;
end;
end;
for i := k downto 1 do
result := s[i] + result;
end;
// 計算
procedure TForm1.CalcBtnClick(Sender: TObject);
var
a, b, z, ans : combig;
eps : bigdecimal;
f : integer;
begin
if inputcheck(precisions) = false then exit;
bigdecimal.DefaultPrecision := precisions;
a.r := aedit.Text;
a.i := iaedit.Text;
b.r := bedit.Text;
b.i := ibedit.Text;
z.r := zedit.Text;
z.i := izedit.Text;
eps := epsedit.Text;
zero := bigdecimal.Zero;
one := bigdecimal.One;
memo1.Clear;
memo1.Lines.Append('第1種合流型超幾何関数');
f := Confluent_Hypergeometri_of_first(a, b, z, eps, ans);
if f = 0 then begin
ans.r := ans.r.RoundToPrecision(50);
ans.i := ans.i.RoundToPrecision(50);
if ans.r = zero then
memo1.Lines.Append('0.0')
else
memo1.Lines.Append(ZeroErase(ans.r.ToString));
if ans.i = zero then
memo1.Lines.Append('0.0 i')
else
memo1.Lines.Append(ZeroErase(ans.i.ToString) + ' i');
end
else begin
if ans.r > zero then memo1.Lines.Append('∞');
if ans.r < zero then memo1.Lines.Append('-∞');
if ans.i > zero then memo1.Lines.Append('+∞ i');
if ans.i < zero then memo1.Lines.Append('-∞ i');
end;
end;
end.
![]() Confluent_Hypergeometric_function_of_first.zip
Confluent_Hypergeometric_function_of_first.zip
三角関数、逆三角関数、その他関数 に戻る