カールソンの楕円積分複素数計算
ＲＣ，ＲＦ，ＲＪの複素数計算プログラムを作成したので、楕円積分 離心率(Ｋ)、積分範囲（Ｘ）指定のプログラムを作成しました。
積分範囲ＸはＸ＝ｓｉｎ（Φ）の範囲です。
角度は、Φ＝ｓｉｎ－１（Ｘ）で、Ｘの値に１以上を指定すると、１迄の値として実数部の値がπ／２となり、１を超えた部分が虚数－Φ’ｉの値となります。
いくら大きな値を指定しても１の値を超えた部分は、虚数になります。
左図のプログラムでは、積分範囲の指定に角度が有りますが、実数部の角度は９０°迄で、実数部に９０°を指定した時のみ、虚数部の角度が指定できます。
虚数部の角度値はマイナスの値を指定します。
ｓｉｎ（Φ）の計算をすると、積分範囲X必ず実数のみの値となり虚数はゼロになります。
積分範囲Ｘの値に１以上を或いは、離心率の値に１以上を指定すると、楕円積分結果に虚数部が現れますが、ＲＦ、ＲＪの引数に虚数部の値は有りません。
離心率ｋの値に１以上を指定した場合は、実際の実数の積分範囲は９０°以下になります。
第三種楕円積分の特性値（ａ）或いは、パラメータ（ｍ）の値に関しては複素数の入力が出来るようにしても、その計算結果がどの様な意味をもっているのか解らないのと、検算も出来ないので、実数のみの入力になっています。
ランデン変換の複素数計算第一二種のランデン変換楕円積分の積分範囲指定の角度は、９０°を超えた場合、９０°分割の計算になっています。
ランデン変換の複素数計算と値が一致するのは、積分範囲Ｘの値が１（ｓｉｎ９０°）迄です。
又、ランデン変換では、離心率ｋの値に１を越えてランデン変換することが出来ないので、１より大きい場合は、１より小さくなるように変換をして計算していますし、負数の場合は、正の値で１以下になる様に変換して計算していますが、カールソンので楕円積分では、その必要性はありません。
高精度計算サイトのフリー計算に、ここのカールソンの複素数のプログラムと同じ計算があるのですが、離心率ｋの値によっては、積分範囲Ｘの値が１．２辺りを越えると計算結果の値があわなくなります、原因は判りませんプログラムにミスは無いと思うのですが。
プログラム（Variant変数使用）
離心率 k = 1
で89.9997°範囲Ｘの値は0.999999999986292で、 第三種の特性値 ａ＝１の時、積分角度８９．８°でこの時の範囲Ｘの値は0.99999390765779でゼロでの除算が発生します。
あきらかに、演算の有効桁数が不足しています。
// 1/31/2021 // プログラムは https://arxiv.org/abs/math/9409227 のレポートを元に作成しています // 離心率k= 1 角度φ=89.9999°近辺でゼロでの除算と桁落ちが発生します // 係数a= 1 角度φ=89.8°近辺でゼロでの除算と桁落ちが発生します unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls, Vcl.Buttons; type TForm1 = class(TForm) Edit1: TEdit; Label1: TLabel; LabeledEdit1: TLabeledEdit; LabeledEdit2: TLabeledEdit; LabeledEdit3: TLabeledEdit; Button1: TButton; Button2: TButton; LabeledEdit4: TLabeledEdit; Edit2: TEdit; Edit3: TEdit; Edit4: TEdit; Edit5: TEdit; Edit6: TEdit; Label2: TLabel; Label3: TLabel; Memo1: TMemo; LabeledEdit5: TLabeledEdit; LabeledEdit6: TLabeledEdit; RadioButton1: TRadioButton; RadioButton2: TRadioButton; procedure Button1Click(Sender: TObject); procedure Button2Click(Sender: TObject); private { Private 宣言 } function datainput(var a, x, k: double; var FI: boolean): boolean; procedure calc_Third_elliptic_integral_complex; public { Public 宣言 } end; var Form1: TForm1; implementation {$R *.dfm} uses system.Math, System.VarCmplx; var ERRF : integer; ZeroF : integer; // 複素数の生成 function Vc(a, b: double): Variant; begin result := varascomplex(result); result.real := a; result.Imaginary := b; end; // ---------------- RC --------------------------------------------------------- function RCC(x, y: variant): variant; label Ext; const r = 1E-24; c1 = 3 / 10; c2 = 1 / 7; c3 = 3 / 8; c4 = 9 / 22; c5 = 159 / 208; c6 = 9 / 8; var xt, yt, w, yb : variant; lamda, A0, Q : variant; s, Am : variant; m : integer; pt : double; begin if Varcomplexabs(y) = 0 then begin // m := 0; result := Vc(0, 0); ZeroF := ZeroF or 1; goto Ext; end; if (y.real > 0) or (y.Imaginary <> 0) then begin xt := x; yt := y; w := Vc(1, 0); end else begin xt := x - y; yt := - y; pt := xt.real * xt.real + xt.Imaginary * xt.Imaginary; if pt < 1E-5 then begin // 演算エラー回避 if xt.real > 0 then xt := Vc(1E-5, 0) else xt := Vc(-1E-5, 0); ERRF := ERRF or 1; end; w := Varcomplexsqrt(x / xt); end; yb := yt; A0 := (xt + yt + yt) / 3; Am := A0; Q := power(3 * r, -1 / 8) * Varcomplexabs(A0 - xt); m := 0; repeat lamda := 2 * Varcomplexsqrt(xt) * Varcomplexsqrt(yt) + yt; xt := (xt + lamda) / 4; yt := (yt + lamda) / 4; Am := (Am + lamda) / 4; m := m + 1; until (power(4, -m) * Q < Varcomplexabs(Am)) or (m > 10); pt := am.real * am.real + am.Imaginary * am.Imaginary; if pt < 1E-5 then begin // 演算エラー回避 if am.real > 0 then am := Vc(1E-5, 0) else am := Vc(-1E-5, 0); ERRF := ERRF or 1; end; s := (yb - A0) / Varcomplexpower(4, m) / Am; result := w * (1 + s * s * (c1 + s * (c2 + s * (c3 + s * (c4 + s * (c5 + s * c6)))))) / Varcomplexsqrt(Am); Ext: // Form1.Memo1.Lines.Append('RC Loop数 = ' + intTostr(m)); end; // ---------------- RF --------------------------------------------------------- // RF function RFC(x, y, z: variant): variant; label Ext; const r = 1E-24; c1 = 1 / 10; c2 = 1 / 14; c3 = 1 / 24; c4 = 3 / 44; var one : variant; lamda : variant; xm, ym, zm : variant; A0, Am, Q : variant; sqrtx, sqrty, sqrtz : variant; m : integer; X0, Y0, Z0 : variant; E2, E3 : variant; pt : double; begin m := 0; if Varcomplexabs(x) = 0 then inc(m); if Varcomplexabs(y) = 0 then inc(m); if Varcomplexabs(z) = 0 then inc(m); if m > 1 then begin // m := 0; result := Vc(0, 0); ZeroF := ZeroF or 2; goto Ext; end; one := Vc(1, 0); xm := x; ym := y; zm := z; A0 := (xm + ym + zm) / 3; Am := A0; Q := power(3 * r, -1 / 6) * max(Varcomplexabs(A0 - xm), max(Varcomplexabs(A0 - ym), Varcomplexabs(A0 - zm))); m := 0; repeat sqrtx := Varcomplexsqrt(xm); sqrty := Varcomplexsqrt(ym); sqrtz := Varcomplexsqrt(zm); lamda := sqrtx * (sqrty + sqrtz) + sqrty * sqrtz; xm := (xm + lamda) / 4; ym := (ym + lamda) / 4; zm := (zm + lamda) / 4; Am := (Am + lamda) / 4; m := m + 1; until power(4, -m) * Q < Varcomplexabs(Am); pt := Am.real * Am.real + Am.Imaginary * Am.Imaginary; if pt < 1E-5 then begin // 演算エラー回避 if Am.real > 0 then Am := Vc(1E-5, 0) else Am := Vc(-1E-5, 0); ERRF := ERRF or 2; end; X0 := (A0 - x) / Varcomplexpower(4, m) / Am; Y0 := (A0 - y) / Varcomplexpower(4, m) / Am; Z0 := -X0 - Y0; E2 := X0 * Y0 - Z0 * Z0; E3 := X0 * Y0 * Z0; result := VarcomplexPower(Am, -1 / 2) * (one - c1 * E2 + c2 * E3 + c3 * E2 * E2 - c4 * E2 * E3); Ext: // Form1.Memo1.Lines.Append('RF Loop数 = ' + intTostr(m)); end; // ---------------- RJ --------------------------------------------------------- function minc3(a, b, c: variant): variant; var tmp : variant; begin if Varcomplexabs(a) < Varcomplexabs(b) then tmp := a else tmp := b; if Varcomplexabs(tmp) < Varcomplexabs(c) then result := tmp else result := c; end; function maxc3(a, b, c: variant): variant; var tmp : variant; begin if Varcomplexabs(a) > Varcomplexabs(b) then tmp := a else tmp := b; if Varcomplexabs(tmp) > Varcomplexabs(c) then result := tmp else result := c; end; // RJ function RJC(x, y, z, p: variant): variant; label Ext; const r = 1E-24; c1 = 3 / 14; c2 = 1 / 6; c3 = 9 / 88; c4 = 3 / 22; c5 = 9 / 52; c6 = 3 / 26; var one : variant; rj, xt, yt, zt, pt : variant; sum, a, b, rho, A0 : variant; tau, rcx, lamda, Q : variant; m, Am : variant; sqrtx, sqrty, sqrtz, sqrtp: variant; delta, dm, em : variant; test : integer; X0, Y0, Z0, P0 : variant; E2, E3, E4, E5 : variant; pm : double; begin m := 0; if Varcomplexabs(x) = 0 then inc(m); if Varcomplexabs(y) = 0 then inc(m); if Varcomplexabs(z) = 0 then inc(m); if Varcomplexabs(p) = 0 then inc(m); if m > 1 then begin // m := 0; result := Vc(0, 0); ZeroF := ZeroF or 4; goto Ext; end; sum := Vc(0, 0); one := Vc(1, 0); if (p.real <= 0) and (y.real > 0) then test := -1 else test := 1; if test > 0 then begin xt := x; yt := y; zt := z; pt := p; a := Vc(0, 0); b := Vc(0, 0); rcx := Vc(0, 0); end else begin xt := minc3(x, y, z); zt := maxc3(x, y, z); yt := x + y + z - xt - zt; if Varcomplexabs(yt - p) > 1E-5 then a := VarComplexInverse(yt - p) // 演算エラー回避 else begin a := 1E100; ERRF := ERRF or 4; end; b := a * (zt - yt) * (yt - xt); pt := yt + b; Pm := yt.real * yt.real + yt.Imaginary * yt.Imaginary; if Pm < 1E-5 then begin // 演算エラー回避 if yt.real > 0 then yt := Vc(1E-5, 0) else yt := Vc(-1E-5, 0); ERRF := ERRF or 4; end; rho := xt * zt / yt; tau := p * pt / yt; rcx := rcc(rho, tau); end; A0 := (xt + yt + zt + pt + pt) / 5; AM := A0; delta := (pt - xt) * (pt - yt) * (pt - zt); Q := power(r / 4, -1 / 6) * max(Varcomplexabs(A0 - xt), max(Varcomplexabs(A0 - yt), max(Varcomplexabs(A0 - zt), Varcomplexabs(A0 - pt)))); m := 0; repeat sqrtx := Varcomplexsqrt(xt); sqrty := Varcomplexsqrt(yt); sqrtz := Varcomplexsqrt(zt); sqrtp := Varcomplexsqrt(pt); lamda := sqrtx * (sqrty + sqrtz) + sqrty * sqrtz; dm := (sqrtp + sqrtx) * (sqrtp + sqrty) * (sqrtp + sqrtz); Pm := dm.real * dm.real + dm.Imaginary * dm.Imaginary; if Pm < 1e-5 then begin if dm.real > 0 then dm := Vc(1E-5, 0) else dm := Vc(-1E-5, 0); ERRF := ERRF or 4; end; em := Varcomplexpower(4, -3 * m) * delta / dm / dm; sum := sum + Varcomplexpower(4, -m) / dm * Rcc(one, one + em); Am := (Am + lamda) / 4; xt := (xt + lamda) / 4; yt := (yt + lamda) / 4; zt := (zt + lamda) / 4; pt := (pt + lamda) / 4; m := m + 1; until power(4, - m) * Q < Varcomplexabs(am); X0 := (A0 - x) / Varcomplexpower(4, m) / Am; Y0 := (A0 - y) / Varcomplexpower(4, m) / Am; Z0 := (A0 - z) / Varcomplexpower(4, m) / Am; P0 := (-X0 - Y0 - Z0) / 2; E2 := X0 * Y0 + X0 * Z0 + Y0 * Z0 - 3 * P0 * P0; E3 := X0 * Y0 * Z0 + 2 * E2 * P0 + 4 * P0 * P0 * P0; Pm := P0.real * P0.real + P0.Imaginary * P0.Imaginary; if Pm > 1e-11 then // !E-11より小さいと0とみなされるので回避 E4 := (2 * X0 * Y0 * Z0 + E2 * P0 + 3 * P0 * P0 * P0) / P0 else begin E4 := Vc(0, 0); // 十分に小さいので計算結果は変わりません // ERRF := ERRF or 4; // 演算結果に影響なし end; E5 := X0 * Y0 * Z0 * P0 * P0; rj := Varcomplexpower(4, -m) * Varcomplexpower(Am, -3 / 2) * (one - c1 * E2 + c2 * E3 + c3 * E2 * E2 - c4 * E4 - c5 * E2 * E3 + c6 * E5) + 6 * sum; if test < 0 then rj := a * (b * rj + 3 * (rcx - rfc(xt, yt, zt))); result := rj; // form1.Canvas.TextOut(250,5,' '); // form1.Canvas.TextOut(250,5,'rj 判定 ' + floatTostr(test)); Ext: // Form1.Memo1.Lines.Append('RJ Loop数 = ' + intTostr(m)); end; // ---------------- Elliptic intehral Calc ------------------------------------- // 楕円積分計算 procedure TForm1.calc_Third_elliptic_integral_complex; var a, k, kmax, x, m : double; xb : double; c : variant; mc, qc : variant; rf0, rj0 : variant; afk : variant; ek, fk : variant; ac : variant; FI : boolean; qmax : double; function rinteg2: variant; // 第二種積分 begin rf0 := RFC(c - 1, c - mc, c); rj0 := RJC(c - 1, c - mc, c, c); result := rf0 - mc / 3 * rj0; end; function rinteg3(a: variant): variant; // 第一三種積分 begin rf0 := RFC(c - 1, c - mc, c); rj0 := RJC(c - 1, c - mc, c, c - a); result := rf0 + a / 3 * rj0; end; begin if not datainput(a, x, k, FI) then exit; ZeroF := 0; ERRF := 0; xb := x; x := abs(x); qc := varcomplexarcsin(x); qmax := pi / 2; m := k * k; if FI then m := -m; // kが虚数だったらm -> -m if m > 1 then begin // パラメータm ,k が１より大きかったら qmax := arcsin(1 / abs(k)); // 実数積分角度位置 end; if x = 0 then begin Edit1.Text := '0'; Edit3.Text := '0'; Edit5.Text := '0'; Edit2.Text := ''; Edit4.Text := ''; Edit6.Text := ''; exit; end; kmax := 1 / sin(qmax); // 実数積分角度位置での最大離心率計算 Memo1.Clear; Memo1.Lines.Append('実数積分角度 = ' + floatTostr(qmax / pi * 180) + '°'); Memo1.Lines.Append('最大離心率 = ±' + floatTostr(kmax)); if x <= 1 then begin Kmax := 1 / x; Memo1.Lines.Append('指定角度の最大離心率 = ±' + floatTostr(kmax)); end; c := 1 / varcomplexsin(qc) / varcomplexsin(qc); mc := Vc(m, 0); ac := Vc(a, 0); if ((a = 1) and (x = 1)) or ((m = 1) and (x = 1)) then begin afk := Vc(infinity, 0); end else begin afk := rinteg3(ac); // 第三種積分 end; if xb < 0 then afk := -afk; Edit1.Text := floatTostr(afk.real); if (m = 1) and (x = 1) then begin ek := Vc(1, 0); // 第二種 1 end else begin ek := rinteg2; // 第二種積分 end; if xb < 0 then ek := -ek; Edit3.Text := floatTostr(ek.real); if (m = 1) and (x = 1) then begin fk := Vc(infinity, 0); // 第一種∞ end else begin ac := Vc(0, 0); fk := rinteg3(ac); // 第一種積分 end; if xb < 0 then fk := -fk; Edit5.Text := floatTostr(fk.real); Edit2.Text := floatTostr(afk.Imaginary) + 'i'; Edit4.Text := floatTostr(ek.Imaginary) + 'i'; Edit6.Text := floatTostr(fk.Imaginary) + 'i'; if ERRF and 1 <> 0 then Memo1.Lines.Text := Memo1.Lines.Text + (#13#10 + 'RCで ゼロでの除算がありました。'); if ERRF and 2 <> 0 then Memo1.Lines.Text := Memo1.Lines.Text + (#13#10 + 'RFで ゼロでの除算がありました。'); if ERRF and 4 <> 0 then Memo1.Lines.Text := Memo1.Lines.Text + (#13#10 + 'RJで ゼロでの除算がありました。'); if ZeroF and 1 <> 0 then Memo1.Lines.Text := Memo1.Lines.Text + (#13#10 + 'RCで 引数 y=0 がありました。'); if ZeroF and 2 <> 0 then Memo1.Lines.Text := Memo1.Lines.Text + (#13#10 + 'RFで 引数 ゼロが二個 がありました。'); if ZeroF and 4 <> 0 then Memo1.Lines.Text := Memo1.Lines.Text + (#13#10 + 'RJで 引数 ゼロが二個 がありました。'); end; // ---------------- 入力処理 --------------------------------------------------- var XF: boolean; // データの入力 // a 第三種楕円積分特性値 n // deg 積分角度 // k 離心率 // FI 離心率 虚数フラグ true で虚数 function TForm1.datainput(var a, x, k: double; var FI: boolean): boolean; var ch, l : integer; degr, degi : double; m : double; degc, xc : Variant; kstr, kss : string; c : char; begin result := False; FI := False; val(LabeledEdit1.Text, a, ch); if ch <> 0 then begin application.MessageBox('a(特性)の値に間違いがあります。','a(特性)',0); exit; end; val(LabeledEdit2.Text, degr, ch); if ch <> 0 then begin application.MessageBox('φ(deg)の値に間違いがあります。','φ(deg)',0); exit; end; if abs(degr) > 90 then begin application.MessageBox('φ(deg)の絶対値値は90°迄です。','φ(deg)',0); exit; end; val(LabeledEdit5.Text, degi, ch); if ch <> 0 then begin application.MessageBox('φ(deg)iの値に間違いがあります。','φ(deg)',0); exit; end; if (abs(degr) < 90) and (degi <> 0) then begin application.MessageBox('φ(deg)が90°以下の場合φ(deg)iの値はゼロです。','φ(deg)',0); exit; end; if (degr * degi > 0) and (abs(degr) >= 90) then begin application.MessageBox('φ(deg)とφ(deg)iの符号は±を逆にして下さい','φ(deg)',0); exit; end; if radiobutton1.Checked = true then begin kstr := LabeledEdit3.Text; l := length(kstr); // 文字の長さ取得 c := kstr[l]; // iの文字確認 if (c = 'i') or (c = 'I') then begin // i虚数指定だったら kss := copy(kstr, 1, l - 1); // iの前までコピー FI := true; // 虚数フラグセット end else Kss := kstr; val(kss, k, ch); if ch <> 0 then begin application.MessageBox('k(離心率)の値に間違いがあります。','k(離心率)',0); exit; end; end; if radiobutton2.Checked = true then begin val(LabeledEdit6.Text, m, ch); if ch <> 0 then begin application.MessageBox('ｍの値に間違いがあります。','m=k^2',0); exit; end; if m < 0 then FI := true; // 虚数フラグセット k := sqrt(abs(m)); // k =√m end; degc := varascomplex(degc); xc := varascomplex(xc); // q := deg * pi / 180; degc.real := degr / 180 * pi; degc.Imaginary := degi / 180 * pi ; if not XF then begin xc := varcomplexsin(degc); LabeledEdit4.Text := floattostr(xc.real); x := xc.real; end else x := strtofloat(LabeledEdit4.Text); result := true; end; // 角度入力 procedure TForm1.Button1Click(Sender: TObject); begin XF := False; calc_Third_elliptic_integral_complex; end; // Xの値入力 procedure TForm1.Button2Click(Sender: TObject); var x : double; ch : integer; q : variant; begin q := varascomplex(q); val(LabeledEdit4.Text, x, ch); if ch <> 0 then begin application.MessageBox('Xの値に間違いがあります。','X(1≧X≧-1)',0); exit; end; XF := True; q := varcomplexarcsin(x); LabeledEdit2.Text := floatTostr(q.real / pi * 180); LabeledEdit5.Text := floatTostr(q.Imaginary / pi * 180); calc_Third_elliptic_integral_complex; end; end.
ＤｏｕｂｌｅとＶａｒｉａｎｔの組み合わせプログラム
ＲＣ，ＲＦ，ＲＪの計算に、ｄｏｕｂｌｅの複素数を出来る限り使用した場合。
（データーの入出力は、Ｖａｒｉａｎｔのまゝです。）
ａ＝１ ｋ＝１ でも、８９．９９９９°迄は、ゼロでの除算が発生しません。
角度のを入力にＶａｒｉａｎｔの複素数を使用しているので、入出力も全て、Ｄｏｕｂｌｅ使用すれば、もう少し、ゼロでの除算の改善が出来るかもしれませんが、全て多倍長複素数のプログラムを作成したので、このプログラムの改善はここ迄としました。
Doubleの複素数の平方根に関しては、VariantのVarcomplexに用意されている、平方根の方が、精度が高いことが判明しました。
Doubleではなく、Extendedを使用するとほゞ同じ精度の複素数の平方根を得ることができます。
// 1/31/2021 // プログラムは https://arxiv.org/abs/math/9409227 のレポートを元に作成しています。 // sin sqrt power はdelphiのVarComplexを使用します。 // 離心率k=1 角度φ=89.99995°近辺で桁落ちによる演算エラーが発生します。 // 係数a= 1 角度φ=89.99995°近辺でゼロでの除算と桁落ちが発生します。 unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls, Vcl.Buttons; type TForm1 = class(TForm) Edit1: TEdit; Label1: TLabel; LabeledEdit1: TLabeledEdit; LabeledEdit2: TLabeledEdit; LabeledEdit3: TLabeledEdit; Button1: TButton; Button2: TButton; LabeledEdit4: TLabeledEdit; Edit2: TEdit; Edit3: TEdit; Edit4: TEdit; Edit5: TEdit; Edit6: TEdit; Label2: TLabel; Label3: TLabel; Memo1: TMemo; LabeledEdit5: TLabeledEdit; RadioButton1: TRadioButton; RadioButton2: TRadioButton; LabeledEdit6: TLabeledEdit; procedure Button1Click(Sender: TObject); procedure Button2Click(Sender: TObject); private { Private 宣言 } function datainput(var a, x, k: double; var FI: boolean): boolean; procedure calc_Third_elliptic_integral_complex; public { Public 宣言 } end; var Form1: TForm1; implementation {$R *.dfm} uses system.Math, System.VarCmplx; var ZeroF : integer; ERRF : integer; // 複素数の生成 function Varcomplex(a, b: double): Variant; begin result := varascomplex(result); result.real := a; result.Imaginary := b; end; // 複素数構造体 type TCdouble = record r : double; i : double; end; // 複素数の生成 function Vc(a, b: double): Variant; begin result := varascomplex(result); result.real := a; result.Imaginary := b; end; // 複素数変換 Varint to TCdouble function VtoT(x : variant): TCdouble; begin result.r := x.real; result.i := x.Imaginary; end; // 複素数変換 TCdouble to variant; function TtoV(x : TCdouble): variant; begin result := varascomplex(result); result.real := x.r; result.Imaginary := x.i; end; // TCdouble複素数の生成 function MCdouble(r, i: double): TCdouble; begin result.r := r; result.i := i; end; // TCdouble複素数の加算 function cadd(a, b: TCdouble): TCdouble; begin result.r := a.r + b.r; result.i := a.i + b.i; end; // TCdouble複素数の減算 function csub(a, b: TCdouble): TCdouble; begin result.r := a.r - b.r; result.i := a.i - b.i; end; // TCdouble複素数の乗算 function cmul(a, b: TCdouble): TCdouble; begin result.r := a.r * b.r - a.i * b.i; result.i := a.r * b.i + a.i * b.r; end; // TCdouble複素数とDoubleの乗算 function cmuld(a: TCdouble; b: double): TCdouble; begin result.r := a.r * b; result.i := a.r * b; end; // TCdouble複素数とDoubleの除算 function cdivd(a: TCdouble; b: double): TCdouble; begin result.r := a.r / b; result.i := a.i / b; end; // TCdouble複素数の除算 function cdiv(a, b: TCdouble): TCdouble; var bb: double; begin result.r := 0; result.i := 0; bb := b.r * b.r + b.i * b.i; if bb <> 0 then begin result.r := (a.r * b.r + a.i * b.i) / bb; result.i := (a.i * b.r - a.r * b.i) / bb; end; end; // TCdouble複素数の符号反転 function cchs(a: TCdouble): TCdouble; begin result.r := -a.r; result.i := -a.i; end; // 複素数の平方根 function tsqrt(x: TCdouble): TCdouble; var xv, xs : variant; begin xv := varcomplex(x.r, x.i); xs := varcomplexsqrt(xv); result := MCdouble(xs.real, xs.imaginary); end; // 複素数 x^y 演算variant complex function tpower(x: TCdouble; p : double): TCdouble; var xv, xs : variant; begin xv := varcomplex(x.r, x.i); xs := varcomplexpower(xv, p); result := MCdouble(xs.real, xs.Imaginary); end; // 複素数の絶対値 function cabs(x: TCdouble): double; var a : double; begin a := x.r * x.r + x.i * x.i; result := sqrt(a); end; // ---------------- RC --------------------------------------------------------- // RC function RCd(x, y: TCdouble): TCdouble; label Ext; const r = 1E-24; c1d = 3 / 10; c2d = 1 / 7; c3d = 3 / 8; c4d = 9 / 22; c5d = 159 / 208; c6d = 9 / 8; var xt, yt : TCdouble; lamda, Am : TCdouble; A0, s, yb : TCdouble; one, p4, w : TCdouble; c1, c2, c3, c4, c5, c6 : TCdouble; d2 : TCdouble; tmp : TCdouble; Q : Double; m : integer; begin if cabs(y) = 0 then begin // yがゼロだったら終了 result := MCdouble(0, 0); // m := 0; ZeroF := ZeroF or 1; goto Ext; end; one := MCdouble(1, 0); c1 := MCdouble(c1d, 0); c2 := MCdouble(c2d, 0); c3 := MCdouble(c3d, 0); c4 := MCdouble(c4d, 0); c5 := MCdouble(c5d, 0); c6 := MCdouble(c6d, 0); d2 := MCdouble(2, 0); if (y.r > 0) or (y.i <> 0) then begin xt := x; yt := y; w := MCdouble(1, 0); end else begin xt := csub(x, y); yt := cchs(y); w := tsqrt(cdiv(x, xt)); end; yb := yt; A0 := cdivd(cadd(xt,cadd(yt, yt)), 3); Am := A0; Q := 1 / power(3 * r, 1 / 8) * cabs(csub(A0, xt)); m := 0; repeat lamda := cadd(cmul(d2, cmul(tsqrt(xt), tsqrt(yt))), yt); xt := cdivd(cadd(xt, lamda), 4); yt := cdivd(cadd(yt, lamda), 4); Am := cdivd(cadd(Am, lamda), 4); inc(m); until power(4, -m) * Q < cabs(Am); p4 := MCdouble(power(4, m), 0); s := cdiv(cdiv(csub(yb, A0), p4), Am); tmp := cadd(c5, cmul(s, c6)); tmp := cadd(c4, cmul(s, tmp)); tmp := cadd(c3, cmul(s, tmp)); tmp := cadd(c2, cmul(s, tmp)); tmp := cadd(c1, cmul(s, tmp)); tmp := cadd(one, cmul(s, cmul(s, tmp))); result := cdiv(cmul(w, tmp), tsqrt(Am)); // varcomplexsqrtを使用します Ext: // Form1.Memo1.Lines.Append('RC Loop数 = ' + intTostr(m)); end; // ---------------- RF --------------------------------------------------------- // RF function RFd(x, y, z: TCdouble): TCdouble; label Ext; const r = 1E-30; c1d = 1 / 10; c2d = 1 / 14; c3d = 1 / 24; c4d = 3 / 44; var one : TCdouble; lamda : TCdouble; xm, ym, zm : TCdouble; A0, Am : TCdouble; sqrtx, sqrty, sqrtz : TCdouble; m : integer; X0, Y0, Z0 : TCdouble; E2, E3 : TCdouble; c1, c2, c3, c4 : TCdouble; d3, d4, p4, tmp : TCdouble; Q : double; begin m := 0; if cabs(x) = 0 then inc(m); if cabs(y) = 0 then inc(m); if cabs(z) = 0 then inc(m); if m > 1 then begin // ゼロが二個有ったら終了 // m := 0; result := MCdouble(0, 0); ZeroF := ZeroF or 2; goto Ext; end; one := MCdouble(1, 0); c1 := MCdouble(c1d, 0); c2 := MCdouble(c2d, 0); c3 := MCdouble(c3d, 0); c4 := MCdouble(c4d, 0); d3 := MCdouble(3, 0); d4 := MCdouble(4, 0); xm := x; ym := y; zm := z; A0 := cdiv(cadd(xm, cadd(ym, zm)), d3); Am := A0; Q := power(3 * r, -1 / 6) * max(cabs(csub(A0, xm)), max(cabs(csub(A0, ym)), cabs(csub(A0, zm)))); m := 0; repeat sqrtx := tsqrt(xm); sqrty := tsqrt(ym); sqrtz := tsqrt(zm); lamda := cadd(cmul(sqrtx,(cadd(sqrty, sqrtz))), cmul(sqrty,sqrtz)); xm := cdivd(cadd(xm, lamda), 4); ym := cdivd(cadd(ym, lamda), 4); zm := cdivd(cadd(zm, lamda), 4); Am := cdivd(cadd(Am, lamda), 4); m := m + 1; until power(4, -m) * Q < cabs(Am); p4 := MCdouble(power(4, m), 0); X0 := cdiv(cdiv(csub(A0, x), p4), Am); Y0 := cdiv(cdiv(csub(A0, y), p4), Am); Z0 := csub(cchs(X0), Y0); E2 := csub(cmul(X0, Y0), cmul(Z0, Z0)); E3 := cmul(X0, cmul(Y0, Z0)); tmp := csub(one, cmul(c1, E2)); tmp := cadd(tmp, cmul(c2, E3)); tmp := cadd(tmp, cmul(E2, cmul(c3, E2))); tmp := csub(tmp, cmul(E3,cmul(c4, E2))); result := cmul(cdiv(one, tsqrt(Am)), tmp); // varcomplexsqrtを使用します Ext: // Form1.Memo1.Lines.Append('RF Loop数 = ' + intTostr(m)); end; // ---------------- RJ --------------------------------------------------------- // 複素数３個の最小値 function minc3d(a, b, c: TCdouble): TCdouble; var tmp : TCdouble; begin if cabs(a) < cabs(b) then tmp := a else tmp := b; if cabs(tmp) < cabs(c) then result := tmp else result := c; end; // 複素数３個の最大値 function maxc3d(a, b, c: TCdouble): TCdouble; var tmp : TCdouble; begin if cabs(a) > cabs(b) then tmp := a else tmp := b; if cabs(tmp) > cabs(c) then result := tmp else result := c; end; // RJ function RJd(x, y, z, p: TCdouble): TCdouble; label Ext; const r = 1E-30; var one : TCdouble; rj, xt, yt, zt, pt : TCdouble; sum, a, b, rho, A0 : TCdouble; tau, rcx, lamda, Am : TCdouble; sqrtx, sqrty, sqrtz, sqrtp, dm, em : TCdouble; delta : TCdouble; c1, c2, c3 : TCdouble; c4, c5, c6 : TCdouble; X0, Y0, Z0, P0 : TCdouble; E2, E3, E4, E5 : TCdouble; d0, d2, d3, d4, d5, d6 : TCdouble; p4 : TCdouble; powa, def : TCdouble; Q, pm : double; test, m : integer; begin m := 0; if cabs(x) = 0 then inc(m); if cabs(y) = 0 then inc(m); if cabs(z) = 0 then inc(m); if cabs(p) = 0 then inc(m); if m > 1 then begin // ゼロが二個有ったら終了 // m := 0; result := MCdouble(0, 0); ZeroF := ZeroF or 4; goto Ext; end; c1 := MCdouble(3 / 14, 0); c2 := MCdouble(1 / 6, 0); c3 := MCdouble(9 / 88, 0); c4 := MCdouble(3 / 22, 0); c5 := MCdouble(9 / 52, 0); c6 := MCdouble(3 / 26, 0); d0 := MCdouble(0, 0); d2 := MCdouble(2, 0); d3 := MCdouble(3, 0); d4 := MCdouble(4, 0); d5 := MCdouble(5, 0); d6 := MCdouble(6, 0); sum := MCdouble(0, 0); one := MCdouble(1, 0); if (p.r <= 0) and (y.r > 0) then test := -1 else test := 1; if test > 0 then begin xt := x; yt := y; zt := z; pt := p; a := MCdouble(0, 0); b := MCdouble(0, 0); rcx := MCdouble(0, 0); end else begin xt := minc3d(x, y, z); zt := maxc3d(x, y, z); yt := cadd(x, cadd(y, csub(z, cadd(xt, zt)))); if cabs(csub(yt, p)) <> 0 then a := cdiv(one, csub(yt, p)) // 演算エラー回避 else begin a := MCdouble(+1E100, 0); ERRF := ERRF or 4; end; b := cmul(cmul(a, csub(zt, yt)), csub(yt, xt)); pt := cadd(yt, b); rho := cmul(xt, cdiv(zt, yt)); tau := cmul(p, cdiv(pt, yt)); rcx := rcd(rho, tau); end; A0 := cdiv(cadd(xt, cadd(yt, cadd(zt, cadd(pt, pt)))), d5); AM := A0; delta := cmul(csub(pt, xt), cmul(csub(pt, yt), csub(pt, zt))); Q := power(r / 4, -1 / 6) * max(cabs(csub(A0, xt)), max(cabs(csub(A0, yt)), max(cabs(csub(A0, zt)), cabs(csub(A0, pt))))); m := 0; repeat sqrtx := tsqrt(xt); sqrty := tsqrt(yt); sqrtz := tsqrt(zt); sqrtp := tsqrt(pt); lamda := cadd(cmul(sqrtx, cadd(sqrty, sqrtz)), cmul(sqrty, sqrtz)); dm := cmul(cadd(sqrtp, sqrtx), cmul(cadd(sqrtp, sqrty), cadd(sqrtp,sqrtz))); p4 := tpower(d4, -3 * m); em := cdiv(cdiv(cmul(p4, delta), dm), dm); p4 := tpower(d4, -m); def := Rcd(one, cadd(one, em)); sum := cadd(sum, cmul(cdiv(p4, dm), def)); Am := cdivd(cadd(Am, lamda), 4); xt := cdivd(cadd(xt, lamda), 4); yt := cdivd(cadd(yt, lamda), 4); zt := cdivd(cadd(zt, lamda), 4); pt := cdivd(cadd(pt, lamda), 4); m := m + 1; until power(4, -m) * Q < cabs(am); p4 := tpower(d4, m); X0 := cdiv(cdiv(csub(A0, x), p4), Am); Y0 := cdiv(cdiv(csub(A0, y), p4), Am); Z0 := cdiv(cdiv(csub(A0, z), p4), Am); P0 := cdivd(csub(csub(csub(d0, X0), Y0), Z0), 2); E2 := csub(cmul(Y0, Z0), cmul(d3, cmul(P0, P0))); E2 := cadd(cmul(X0, Y0), cadd(cmul(X0, Z0), E2)); E3 := cmul(d4, cmul(P0, cmul(P0, P0))); E3 := cadd(cmul(X0, cmul(Y0, Z0)), cadd(cmul(d2, cmul(E2, P0)), E3)); Pm := P0.r * P0.r + P0.i * P0.i; if Pm > 1e-100 then begin // 分母ゼロ回避 E4 := cadd(cmul(E2, P0), cmul(d3, cmul(P0, cmul(P0, P0)))); E4 := cadd(cmul(d2, cmul(X0, cmul(Y0, Z0))), E4); E4 := cdiv(E4, P0); end else E4 := MCdouble(0, 0); E5 := cmul(X0, cmul(Y0, cmul(Z0, cmul(P0, P0)))); p4 := tpower(d4, -m); powa := tpower(Am, -3 / 2); def := csub(one, cmul(c1, E2)); def := cadd(def, cmul(c2, E3)); def := cadd(def, cmul(c3, cmul(E2, E2))); def := csub(def, cmul(c4, E4)); def := csub(def, cmul(c5, cmul(E2, E3))); def := cadd(def, cmul(c6, E5)); rj := cadd(cmul(p4, cmul(powa, def)), cmul(d6, sum)); if test < 0 then rj := cmul(a, (cadd(cmul(b ,rj), cmul(d3, csub(rcx, rfd(xt, yt, zt)))))); result := rj; // form1.Canvas.TextOut(250,320,' '); // form1.Canvas.TextOut(250,320,'rj 判定 ' + floatTostr(test)); Ext: // Form1.Memo1.Lines.Append('RJ Loop数 = ' + intTostr(m)); end; // ---------------- Elliptic intehral Calc ------------------------------------- // 楕円積分計算 procedure TForm1.calc_Third_elliptic_integral_complex; var a, k, kmax, x, m : double; c, xc : variant; mc : variant; rf0, rj0 : variant; rft, rjt : TCdouble; afk : variant; ek, fk : variant; ac : variant; tc1, tcm, tc : TCdouble; tca : TCdouble; FI : boolean; qmax, xb : double; function rinteg2: variant; // 第二種積分 begin tc1 := VtoT(c - 1); tcm := VtoT(c - mc); tc := VtoT(c); rft := RFd(tc1, tcm, tc); rjt := RJd(tc1, tcm, tc, tc); rf0 := TtoV(rft); rj0 := TtoV(rjt); result := rf0 - mc / 3 * rj0; end; function rinteg3(a: variant): variant; // 第一三種積分 begin tc1 := VtoT(c - 1); tcm := VtoT(c - mc); tc := VtoT(c); tca := VtoT(c - a); rft := RFd(tc1, tcm, tc); rjt := RJd(tc1, tcm, tc, tca); rf0 := TtoV(rft); rj0 := TtoV(rjt); result := rf0 + a / 3 * rj0; end; begin if not datainput(a, x, k, FI) then exit; ERRF := 0; ZeroF := 0; xc := varascomplex(xc); xb := x; x := abs(x); xc.real := x; xc.Imaginary := 0; qmax := pi / 2; m := k * k; if FI then m := -m; // kが虚数だったらm -> -m if m > 1 then begin // パラメータm ,k が１より大きかったら qmax := arcsin(1 / abs(k)); // 実数積分角度位置 end; if x = 0 then begin Edit1.Text := '0'; Edit3.Text := '0'; Edit5.Text := '0'; Edit2.Text := ''; Edit4.Text := ''; Edit6.Text := ''; exit; end; kmax := 1 / sin(qmax); // 実数積分角度位置での最大離心率計算 Memo1.Clear; Memo1.Lines.Append('実数積分角度 = ' + floatTostr(qmax / pi * 180) + '°'); Memo1.Lines.Append('最大離心率 = ±' + floatTostr(kmax)); if x <= 1 then begin kmax := 1 / x; // 実数積分角度位置での最大離心率計算 Memo1.Lines.Append('指定角度の最大離心率 = ±' + floatTostr(kmax)); end; c := 1 / xc / xc; mc := Vc(m, 0); ac := Vc(a, 0); if ((a = 1) and (x = 1)) or ((m = 1) and (x = 1)) then begin afk := Vc(infinity, 0); end else begin afk := rinteg3(ac); // 第三種積分 end; if xb < 0 then afk := -afk; Edit1.Text := floatTostr(afk.real); if (m = 1) and (x = 1) then begin ek := Vc(1, 0); // 第二種 1 end else begin ek := rinteg2; // 第二種積分 end; if xb < 0 then ek := -ek; Edit3.Text := floatTostr(ek.real); if (m = 1) and (x = 1) then begin fk := Vc(infinity, 0); // 第一種∞ end else begin ac := Vc(0, 0); fk := rinteg3(ac); // 第一種積分 end; if xb < 0 then fk := -fk; Edit5.Text := floatTostr(fk.real); Edit2.Text := floatTostr(afk.Imaginary) + 'i'; Edit4.Text := floatTostr(ek.Imaginary) + 'i'; Edit6.Text := floatTostr(fk.Imaginary) + 'i'; if ERRF and 4 <> 0 then Memo1.Lines.Text := Memo1.Lines.Text + ('RJ ゼロでの除算がありました。'); if ZeroF and 1 <> 0 then Memo1.Lines.Text := Memo1.Lines.Text + (#13#10 + 'RCで 引数 y=0 がありました。'); if ZeroF and 2 <> 0 then Memo1.Lines.Text := Memo1.Lines.Text + (#13#10 + 'RFで 引数 ゼロが二個 がありました。'); if ZeroF and 4 <> 0 then Memo1.Lines.Text := Memo1.Lines.Text + (#13#10 + 'RJで 引数 ゼロが二個 がありました。'); end; // ---------------- 入力処理 --------------------------------------------------- var XF: boolean; // データの入力 // a 第三種楕円積分特性値 n // deg 積分角度 // k 離心率 // FI 離心率 虚数フラグ true で虚数 function TForm1.datainput(var a, x, k: double; var FI: boolean): boolean; var ch, l : integer; degr, degi : double; m : double; degc, xc : Variant; kstr, kss : string; c : char; begin result := False; FI := False; val(LabeledEdit1.Text, a, ch); if ch <> 0 then begin application.MessageBox('a(特性)の値に間違いがあります。','a(特性)',0); exit; end; val(LabeledEdit2.Text, degr, ch); if ch <> 0 then begin application.MessageBox('φ(deg)の値に間違いがあります。','φ(deg)',0); exit; end; if abs(degr) > 90 then begin application.MessageBox('φ(deg)の絶対値値は90°迄です。','φ(deg)',0); exit; end; val(LabeledEdit5.Text, degi, ch); if ch <> 0 then begin application.MessageBox('φ(deg)iの値に間違いがあります。','φ(deg)',0); exit; end; if (abs(degr) < 90) and (degi <> 0) then begin application.MessageBox('φ(deg)が90°以下の場合φ(deg)iの値はゼロです。','φ(deg)',0); exit; end; if (degr * degi > 0) and (abs(degr) >= 90) then begin application.MessageBox('φ(deg)とφ(deg)iの符号は±を逆にして下さい','φ(deg)',0); exit; end; if radiobutton1.Checked = true then begin kstr := LabeledEdit3.Text; l := length(kstr); // 文字の長さ取得 c := kstr[l]; // iの文字確認 if (c = 'i') or (c = 'I') then begin // i虚数指定だったら kss := copy(kstr, 1, l - 1); // iの前までコピー FI := true; // 虚数フラグセット end else Kss := kstr; val(kss, k, ch); end; if ch <> 0 then begin application.MessageBox('k(離心率)の値に間違いがあります。','k(離心率)',0); exit; end; if radiobutton2.Checked = true then begin val(LabeledEdit6.Text, m, ch); if ch <> 0 then begin application.MessageBox('ｍの値に間違いがあります。','m=k^2',0); exit; end; if m < 0 then FI := true; // 虚数フラグセット k := sqrt(abs(m)); // k =√m end; degc := varascomplex(degc); xc := varascomplex(xc); // q := deg * pi / 180; degc.real := degr / 180 * pi; degc.Imaginary := degi / 180 * pi ; if not XF then begin xc := varcomplexsin(degc); LabeledEdit4.Text := floattostr(xc.real); x := xc.real; end else x := strtofloat(LabeledEdit4.Text); result := true; end; procedure TForm1.Button1Click(Sender: TObject); begin XF := False; calc_Third_elliptic_integral_complex; end; procedure TForm1.Button2Click(Sender: TObject); var x : double; xc : variant; ch : integer; q : variant; begin val(LabeledEdit4.Text, x, ch); if ch <> 0 then begin application.MessageBox('Xの値に間違いがあります。','X(1≧X≧-1)',0); exit; end; XF := True; q := varascomplex(q); xc := varascomplex(xc); xc.real := x; xc.Imaginary := 0;; q := varcomplexarcsin(xc); LabeledEdit2.Text := floatTostr(q.real / pi * 180); LabeledEdit5.Text := floatTostr(q.Imaginary / pi * 180); calc_Third_elliptic_integral_complex; end; end.
多倍長演算による楕円積分
多倍長の組み込みは MPArithからmparith_2018-11-27.zipをダウンロードして下さい。
Zipファイルを解凍して、解凍したフォルダーにパス(ツール->オプション->Delphiオプション->ライブラリ->ライブラリパス)を追加し、Uses に mp_types, mp_real, mp_cmplx,
mp_baseを追加すれば使用可能になります。
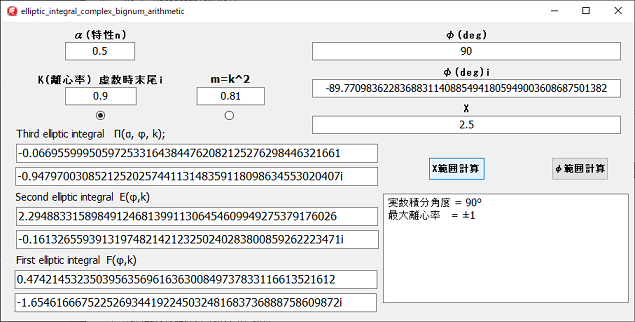各値の入力条件は、Ｖａｒｉａｎｔ複素数の計算と同じです。
演算の有効桁数が７４桁と多いので、桁落ちによるゼロでの除算は発生しません。
（全ての条件でテストはしていませんので発生の可能性はあります。）
複素数の演算は、非常に演算時間がかかります。
値が無限大になる条件の場合、値にＭａｘｄｏｕｂｌｅの値を返すと同時に無限大のフラグを使用して、無限大の表示をしています。
多倍長の値にＩｎｆｉｎｉｔｙが無い為です。
演算精度として５０桁程度出る様に、収束判定値を設定しています。
データーの入力は、テキストから直接多倍長に変換するルーチンを使用しています、一旦Doubleに変換してから多倍長にした方が簡単なのですが、Doubleに変換するときの桁落ちをなくす為です。
入力データーの入力ミスの確認は、Doubleで確認し、実際の多倍長への入力は、直接変換しているので、コンパイル時、Doubleの変数に入力された値が使用されていませんと、警告がでますが無視をして下さい。
多倍長プログラム
プログラムの内容は、Ｖａｒｉａｎｔ複素数と同じですが、多倍長は Function が使用出来ないので、非常に長くなっています。
// 1/31/2021 // プログラムは https://arxiv.org/abs/math/9409227 のレポートを元に作成しています // 引数のエラー 桁落ちによるゼロでの除算回避を入れてありますが桁数が多い為発生しないようです。 unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls, Vcl.Buttons, mp_real, mp_cmplx, mp_types, mp_base; type TForm1 = class(TForm) Edit1: TEdit; Label1: TLabel; LabeledEdit1: TLabeledEdit; LabeledEdit2: TLabeledEdit; LabeledEdit3: TLabeledEdit; Button1: TButton; Button2: TButton; LabeledEdit4: TLabeledEdit; Edit2: TEdit; Edit3: TEdit; Edit4: TEdit; Edit5: TEdit; Edit6: TEdit; Label2: TLabel; Label3: TLabel; Memo1: TMemo; LabeledEdit5: TLabeledEdit; RadioButton1: TRadioButton; RadioButton2: TRadioButton; LabeledEdit6: TLabeledEdit; procedure Button1Click(Sender: TObject); procedure Button2Click(Sender: TObject); private { Private 宣言 } function datainput(var ac, xc, kc: mp_complex): boolean; procedure calc_Third_elliptic_integral_complex; public { Public 宣言 } end; var Form1: TForm1; implementation {$R *.dfm} uses system.Math; var ERRF : integer; ZeroF : integer; //============================================================================== procedure mpf_max(x, y: mp_float; var ans: mp_float); begin if mpf_is_gt(x, y) then mpf_copy(x, ans) else mpf_copy(y, ans); end; // ---------------- RC --------------------------------------------------------- // RC procedure RCd(x, y: mp_complex; var ans: mp_complex); label Ext; const r = 1E-200; c1d = 3 / 10; c2d = 1 / 7; c3d = 3 / 8; c4d = 9 / 22; c5d = 159 / 208; c6d = 9 / 8; var xt, yt : mp_complex; lamda, Am : mp_complex; A0, s, yb : mp_complex; one, p4, w : mp_complex; c1, c2, c3 : mp_complex; c4, c5, c6 : mp_complex; d2 : mp_complex; sqrtx, sqrty : mp_complex; tmp, tmpa : mp_complex; Q, tmpf, tmpaf : mp_float; m : integer; begin mpc_init2(xt, yt); mpc_init2(lamda, Am); mpc_init3(A0, s, yb); mpc_init3(one, p4, w); mpc_init3(c1, c2, c3); mpc_init3(c4, c5, c6); mpc_init2(sqrtx, sqrty); mpc_init2(tmp, tmpa); mpc_init(d2); mpf_init3(Q, tmpf, tmpaf); mpc_abs(y, tmpf); if mpf_is0(tmpf) then begin // yがゼロだったら終了 mpc_set_dbl(ans, 0, 0); ZeroF := ZeroF or 1; goto Ext; end; mpc_set_dbl(one, 1, 0); mpc_set_dbl(c1, c1d, 0); mpc_set_dbl(c2, c2d, 0); mpc_set_dbl(c3, c3d, 0); mpc_set_dbl(c4, c4d, 0); mpc_set_dbl(c5, c5d, 0); mpc_set_dbl(c6, c6d, 0); mpc_set_dbl(d2, 2, 0); if s_mpf_is_gt0(y.re) or not s_mpf_is0(y.im) then begin mpc_copy(x, xt); mpc_copy(y, yt); mpc_set1(w); end else begin mpc_sub(x, y, xt); mpc_chs(y, yt); mpc_div(x, xt, w); mpc_sqrt(w, w); end; mpc_copy(yt, yb); // yb = yt mpc_add(yt, yt, tmp); // yt + yt mpc_add(tmp, xt, tmp); // 2yt + xt mpc_div_dbl(tmp, 3, A0); // (2yt + xt) / 3 mpc_copy(A0, Am); // Am = A0 mpf_set_dbl(tmpf, 3 * r); // 3 * r mpf_set_dbl(tmpaf, 1 / 8); // 1 / 8 mpf_expt(tmpf, tmpaf, tmpf); // power(3 * r, 1 / 8) mpf_inv(tmpf, tmpf); // 1 / power(3 * r, 1 / 8) mpc_sub(A0, xt, tmpa); // A0 - xt mpc_abs(tmpa, tmpaf); // abs(A0 - xt) mpf_mul(tmpf, tmpaf, Q); // Q = 1 / power(3 * r, 1 / 8) * abs(A0 - xt) m := 0; repeat mpc_sqrt(xt, sqrtx); // √x mpc_sqrt(yt, sqrty); // √y mpc_mul(sqrtx, sqrty, tmp); // sqrtx * sqrty mpc_mul(d2, tmp, tmpa); // 2 * (sqrtx * sqrty) mpc_add(tmpa, yt, lamda); // lamda = 2 * (sqrtx * sqrty) + y mpc_add(xt, lamda, tmp); // x + lamda mpc_div_dbl(tmp, 4.0, xt); // x = (x + lamda) / 4 mpc_add(yt, lamda, tmp); // y + lamda mpc_div_dbl(tmp, 4.0, yt); // y = (y + lamda) / 4 mpc_add(Am, lamda, tmp); // Am + lamda mpc_div_dbl(tmp, 4.0, Am); // Am = (Am + lamda) / 4 inc(m); mpf_set_dbl(tmpf, 4); // 4 mpf_set_dbl(tmpaf, -m); // -m mpf_expt(tmpf, tmpaf, tmpf); // 4^-m mpf_mul(tmpf, Q, tmpaf); // 4^-m * Q mpc_abs(Am, tmpf); // abs(am) until mpf_is_lt(tmpaf,tmpf); // power(4, -m) * Q < cabs(Am) mpf_set_int(tmpf, 4); mpf_set_int(tmpaf, m); mpf_expt(tmpf, tmpaf, tmpf); // 4^m mpf_set_int(tmpaf, 0); mpc_set_mpf(p4, tmpf, tmpaf); // p4 = 4^m + 0i mpc_sub(yb, A0, tmp); // yb - A0 mpc_div(tmp, p4, tmpa); // (yb - A0) / p4 mpc_div(tmpa, Am, s); // s = (yb - A0) / p4 / Am mpc_mul(s, c6, tmpa); mpc_add(tmpa, c5, tmp); mpc_mul(s, tmp, tmpa); mpc_add(tmpa, c4, tmp); mpc_mul(s, tmp, tmpa); mpc_add(tmpa, c3, tmp); mpc_mul(s, tmp, tmpa); mpc_add(tmpa, c2, tmp); mpc_mul(s, tmp, tmpa); mpc_add(tmpa, c1, tmp); mpc_mul(s, tmp, tmpa); mpc_mul(s, tmpa, tmp); mpc_add(one, tmp, tmpa); mpc_mul(w, tmpa, tmp); // w * ??? mpc_sqrt(Am, tmpa); mpc_div(tmp, tmpa, ans); // ans = w * ???? / sqrt(Am) Ext: mpc_clear2(xt, yt); mpc_clear2(lamda, Am); mpc_clear3(A0, s, yb); mpc_clear3(one, p4, w); mpc_clear3(c1, c2, c3); mpc_clear3(c4, c5, c6); mpc_clear2(sqrtx, sqrty); mpc_clear2(tmp, tmpa); mpc_clear(d2); mpf_clear3(Q, tmpf, tmpaf); end; // ---------------- RF --------------------------------------------------------- // RF procedure RFd(x, y, z: mp_complex; var ans : mp_complex); label Ext; const r = 1E-200; c1d = 1 / 10; c2d = 1 / 14; c3d = 1 / 24; c4d = 3 / 44; var one : mp_complex; lamda : mp_complex; xm, ym, zm : mp_complex; A0, Am : mp_complex; sqrtx, sqrty, sqrtz : mp_complex; m : integer; X0, Y0, Z0 : mp_complex; E2, E3 : mp_complex; c1, c2, c3, c4 : mp_complex; d3, d4, p4, tmp : mp_complex; tmpa, tmpb, tmpc : mp_complex; tmpf, tmpaf, tmpbf : mp_float; Q, M4 : mp_float; begin mpc_init2(one, lamda); mpc_init3(xm, ym, zm); mpc_init2(A0, Am); mpc_init3(sqrtx, sqrty, sqrtz); mpc_init3(X0, Y0, Z0); mpc_init2(E2, E3); mpc_init4(c1, c2, c3, c4); mpc_init4(d3, d4, p4, tmp); mpc_init3(tmpa, tmpb, tmpc); mpf_init3(tmpf, tmpaf, tmpbf); mpf_init2(Q, M4); m := 0; mpc_abs(x, tmpf); if mpf_is0(tmpf) then inc(m); mpc_abs(y, tmpf); if mpf_is0(tmpf) then inc(m); mpc_abs(z, tmpf); if mpf_is0(tmpf) then inc(m); if m > 1 then begin // ゼロ二個有ったら終了 mpc_set_dbl(ans, 0, 0); ZeroF := ZeroF or 2; goto Ext; end; mpc_set1(one); mpc_set_dbl(c1, c1d, 0); mpc_set_dbl(c2, c2d, 0); mpc_set_dbl(c3, c3d, 0); mpc_set_dbl(c4, c4d, 0); mpc_set_dbl(d3, 3, 0); mpc_set_dbl(d4, 4, 0); mpf_set_dbl(M4, 4); mpc_copy(x, xm); mpc_copy(y, ym); mpc_copy(z, zm); mpc_add(ym, zm, tmp); // x + y mpc_add(tmp, xm, tmpa); // x + y + z mpc_div(tmpa, d3, A0); // (x + y + z) / 3 mpc_copy(A0, Am); // Am = A0 mpc_sub(A0, xm, tmp); // A0 - x mpc_sub(A0, ym, tmpa); // A0 - Y mpc_sub(A0, zm, tmpb); // A0 - z mpc_abs(tmp, tmpf); // |A0 - x| mpc_abs(tmpa, tmpaf); // |A0 - y| mpc_abs(tmpb, tmpbf); // |A0 - z| mpf_max(tmpf, tmpaf, tmpf); // max(|A0-x|,|A0-y|) mpf_max(tmpf, tmpbf, tmpf); // max(|A0-x|,|A0-y|,|A0-z|) mpf_set_dbl(tmpaf, 3 * r); // (3 * r) mpf_set_dbl(tmpbf, -1 / 6); // -1/6 mpf_expt(tmpaf, tmpbf, tmpaf); // (3 * r)^-1/6 or (3 / r)^1/6 mpf_mul(tmpf, tmpaf, Q); // Q = (3 * r)^-1/6 * max((A0-x),(A0-y),(A0-z)) m := 0; repeat mpc_sqrt(xm, sqrtx); // √x mpc_sqrt(ym, sqrty); // √y mpc_sqrt(zm, sqrtz); // √z mpc_mul(sqrty, sqrtz, tmp); // √y * √z mpc_add(sqrty, sqrtz, tmpa); // √y + √z mpc_mul(tmpa, sqrtx, tmpc); // (√y + √z) * √x mpc_add(tmpc, tmp, lamda); // lamda = √x√y + √x√z + √y√z mpc_add(xm, lamda, tmp); // xm + lamda mpc_div(tmp, d4, xm); // zm = (xm + lamda) / 4 mpc_add(ym, lamda, tmp); // ym + lamda mpc_div(tmp, d4, ym); // ym = (ym + lamda) / 4 mpc_add(zm, lamda, tmp); // zm + lamda mpc_div(tmp, d4, zm); // zm = (zm + lamda) / 4 mpc_add(Am, lamda, tmp); // Am + lamda mpc_div(tmp, d4, Am); // Am = (Am + lamda) / 4 m := m + 1; // inc(m) mpf_set_int(tmpaf, -m); // -m mpf_expt(M4, tmpaf, tmpbf); // 4^-m mpf_mul(tmpbf, Q, tmpf); // 4^-m * Q mpc_abs(Am, tmpaf); // abs(Am) until mpf_is_lt(tmpf, tmpaf); // 4^-m * Q < abs(Am) mpf_set_int(tmpaf, m); // m mpf_expt(M4, tmpaf, tmpf); // 4^m mpf_set0(tmpbf); // 0 mpc_set_mpf(P4, tmpf, tmpbf); // P4 = (4^m, 0i) mpc_sub(A0, x, tmp); // A0 - x mpc_div(tmp, p4, tmpa); // (A0 - x) / 4^m mpc_div(tmpa, Am, X0); // X0 = (A0 - x) / 4^m / Am mpc_sub(A0, y, tmp); // A0 - y mpc_div(tmp, p4, tmpa); // (A0 - y) / 4^m mpc_div(tmpa, Am, Y0); // Y0 = (A0 - y) / 4^m / Am mpc_chs(X0, tmp); // -X0 mpc_sub(tmp, Y0, Z0); // Z0 = -X0 - Y0 mpc_mul(Z0, Z0, tmpa); // Z0^2 mpc_mul(X0, Y0, tmpb); // X0 * Y0 mpc_sub(tmpb, tmpa, E2); // E2 = X0 * Y0 - Z0^2 mpc_mul(X0, Y0, tmpa); // X0 * Y0 mpc_mul(tmpa, Z0, E3); // E3 = X0 * Y0 * Z0 mpc_mul(c1, E2, tmpa); // c1 * E2 mpc_sub(one, tmpa, tmp); // 1 - C1 * E2 mpc_mul(c2, E3, tmpa); // c2 * E3 mpc_add(tmp, tmpa, tmp); // 1 - C1 * E2 + c2 * E3 mpc_mul(c3, E2, tmpa); // c3 * E2 mpc_mul(tmpa, E2, tmpb); // c3 * E2^2 mpc_add(tmp, tmpb, tmp); // 1 - C1 * E2 + c2 * E3 + c3 * E2^2 mpc_mul(c4, E2, tmpa); // c4 * E2 mpc_mul(tmpa, E3, tmpb); // c4 * E2 * E3 mpc_sub(tmp, tmpb, tmp); // 1 - C1 * E2 + c2 * E3 + c3 * E2^2 - c4 * E2 * E3 mpc_sqrt(Am, tmpc); // √Am mpc_div(one, tmpc, tmpb); // 1 / √Am mpc_mul(tmpb, tmp, ans); // ans = 1 / √Am * (1 - C1 * E2 + c2 * E3 + c3 * E2^2 - c4 * E2 * E3 Ext: mpc_clear2(one, lamda); mpc_clear3(xm, ym, zm); mpc_clear2(A0, Am); mpc_clear3(sqrtx, sqrty, sqrtz); mpc_clear3(X0, Y0, Z0); mpc_clear2(E2, E3); mpc_clear4(c1, c2, c3, c4); mpc_clear4(d3, d4, p4, tmp); mpc_clear3(tmpa, tmpb, tmpc); mpf_clear3(tmpf, tmpaf, tmpbf); mpf_clear2(Q, M4); end; // ---------------- RJ --------------------------------------------------------- // 複素数３個の最小値 procedure minc3d(a, b, c: mp_complex; var ans: mp_complex); var tmp : mp_complex; ma, mb, mc : mp_float; begin mpc_init(tmp); mpf_init3(ma, mb, mc); mpc_abs(a, ma); mpc_abs(b, mb); mpc_abs(c, mc); if mpf_is_lt(ma, mb) then mpc_copy(a, tmp) else mpc_copy(b, tmp); mpc_abs(tmp, ma); if mpf_is_lt(mc, ma) then mpc_copy(c, ans) else mpc_copy(tmp, ans); mpc_clear(tmp); mpf_clear3(ma, mb, mc); end; // 複素数３個の最大値 procedure maxc3d(a, b, c: mp_complex; var ans: mp_complex); var tmp : mp_complex; ma, mb, mc : mp_float; begin mpc_init(tmp); mpf_init3(ma, mb, mc); mpc_abs(a, ma); mpc_abs(b, mb); mpc_abs(c, mc); if mpf_is_lt(ma, mb) then mpc_copy(b, tmp) else mpc_copy(a, tmp); mpc_abs(tmp, ma); if mpf_is_lt(mc, ma) then mpc_copy(tmp, ans) else mpc_copy(c, ans); mpc_clear(tmp); mpf_clear3(ma, mb, mc); end; // 複素数4個の最大値 procedure maxc4d(a, b, c, d: mp_complex; var ans: mp_complex); var tmp : mp_complex; ma, mb, mc, md : mp_float; begin mpc_init(tmp); mpf_init4(ma, mb, mc, md); mpc_abs(a, ma); mpc_abs(b, mb); mpc_abs(c, mc); mpc_abs(d, md); if mpf_is_lt(mb, ma) then mpc_copy(a, tmp) else mpc_copy(b, tmp); mpc_abs(tmp, ma); if mpf_is_lt(ma, mc) then mpc_copy(c, tmp); mpc_abs(tmp, ma); if mpf_is_lt(ma, md) then mpc_copy(d, ans) else mpc_copy(tmp, ans); mpc_clear(tmp); mpf_clear4(ma, mb, mc, md); end; // RJ procedure RJd(x, y, z, p: mp_complex; var ans: mp_complex); label Ext; const r = 1E-300; var one : mp_complex; rj, xt, yt, zt, pt : mp_complex; sum, a, b, rho, A0 : mp_complex; tau, rcx, lamda, Am : mp_complex; sqrtx, sqrty, sqrtz, sqrtp : mp_complex; dm, em, delta : mp_complex; c1, c2, c3 : mp_complex; c4, c5, c6 : mp_complex; X0, Y0, Z0, P0 : mp_complex; E2, E3, E4, E5 : mp_complex; d0, d2, d3, d4, d5 : mp_complex; d6, p4, powa, def : mp_complex; tmpa, tmpb, tmpc, tmpd : mp_complex; tmpaf, tmpbf, tmpcf : mp_float; Q, pm : mp_float; test, m : integer; begin mpc_init(one); mpc_init5(rj, xt, yt, zt, pt); mpc_init5(sum, a, b, rho, A0); mpc_init4(tau, rcx, lamda, Am); mpc_init4(sqrtx, sqrty, sqrtz, sqrtp); mpc_init3(dm, em, delta); mpc_init3(c1, c2, c3); mpc_init3(c4, c5, c6); mpc_init4(X0, Y0, Z0, P0); mpc_init4(E2, E3, E4, E5); mpc_init5(d0, d2, d3, d4, d5); mpc_init4(d6, p4, powa, def); mpc_init4(tmpa, tmpb, tmpc, tmpd); mpf_init3(tmpaf, tmpbf, tmpcf); mpf_init2(Q, pm); m := 0; mpc_abs(x, tmpaf); if mpf_is0(tmpaf) then inc(m); mpc_abs(y, tmpaf); if mpf_is0(tmpaf) then inc(m); mpc_abs(z, tmpaf); if mpf_is0(tmpaf) then inc(m); mpc_abs(p, tmpaf); if mpf_is0(tmpaf) then inc(m); if m > 1 then begin // ゼロが二個有ったら終了 mpc_set_dbl(ans, 0, 0); ZeroF := ZeroF or 4; goto Ext; end; mpc_set_dbl(c1, 3 / 14, 0); mpc_set_dbl(c2, 1 / 6, 0); mpc_set_dbl(c3, 9 / 88, 0); mpc_set_dbl(c4, 3 / 22, 0); mpc_set_dbl(c5, 9 / 52, 0); mpc_set_dbl(c6, 3 / 26, 0); mpc_set_dbl(d0, 0, 0); mpc_set_dbl(d2, 2, 0); mpc_set_dbl(d3, 3, 0); mpc_set_dbl(d4, 4, 0); mpc_set_dbl(d5, 5, 0); mpc_set_dbl(d6, 6, 0); mpc_set_dbl(sum, 0, 0); mpc_set_dbl(one, 1, 0); if s_mpf_is_le0(p.re) and s_mpf_is_gt0(y.re) then test := -1 else test := 1; if test > 0 then begin mpc_copy(x, xt); mpc_copy(y, yt); mpc_copy(z, zt); mpc_copy(p, pt); mpc_set_dbl(a, 0, 0); mpc_set_dbl(b, 0, 0); mpc_set_dbl(rcx, 0, 0); end else begin minc3d(x, y, z, xt); // xt = min(x, y, z) maxc3d(x, y, z, zt); // zt = max(x, y, z) mpc_add(xt, zt, tmpa); // xt + zt mpc_sub(z, tmpa, tmpb); // z - (xt + zt); mpc_add(y, tmpb, tmpc); // z - (xt + zt) + y; mpc_add(x, tmpc, yt); // yt := z - (xt + zt) + y + x mpc_sub(yt, p, tmpa); // yt - p mpc_abs(tmpa, tmpaf); // |yt - p| if not s_mpf_is0(tmpaf) then begin // 分母ゼロ回避 mpc_inv(tmpa, a); // a = 1 / (yt - p) end else begin mpc_set_dbl(a, 1E200, 0); ERRF := ERRF or 4; end; mpc_sub(yt, xt, tmpa); // yt - xt mpc_sub(zt, yt, tmpb); // zt - yt mpc_mul(a, tmpa, tmpc); // a * (yt - xt) mpc_mul(tmpc, tmpb, b); // b = a * (yt - xt) * (zt - yt) mpc_add(yt, b, pt); // pt = yt + b mpc_abs(yt, tmpaf); // |yt| if not s_mpf_is0(tmpaf) then begin // 分母ゼロ回避 mpc_mul(xt, zt, tmpa); // xt * zt; mpc_div(tmpa, yt, rho); // rho = xt * zt / yt mpc_mul(p, pt, tmpb); // p * pt mpc_div(tmpb, yt, tau); // tau := p * pt / yt end else begin mpc_set_dbl(rho, 1E200, 0); mpc_set_dbl(tau, 1E200, 0); ERRF := ERRF or 16 + 1; end; rcd(rho, tau, rcx); // rcx := rc(rho, tau); end; mpc_add(pt, pt, tmpa); // 2pt mpc_add(tmpa, zt, tmpb); // zt + 2pt mpc_add(tmpb, yt, tmpa); // yt + zt + 2pt mpc_add(tmpa, xt, tmpb); // xt + yt + zt + 2pt mpc_div(tmpb, d5, A0); // A0 = (xt + yt + zt + 2pt) / 5 mpc_copy(A0, Am); // Am = A0 mpc_sub(pt, xt, tmpa); // pt - xt mpc_sub(pt, yt, tmpb); // pt - yt mpc_sub(pt, zt, tmpc); // pt - zt mpc_mul(tmpa, tmpb, tmpd); // ( pt - xt) * (pt - yt) mpc_mul(tmpd, tmpc, delta); // delta = ( pt - xt) * (pt - yt) * pt - zt mpf_set_dbl(tmpaf, r / 4); // r / 4 mpf_set_dbl(tmpbf, -1 / 6); // -1 / 6 mpf_expt(tmpaf, tmpbf, tmpcf); // (r / 4)^(-1 / 6) mpc_sub(A0, xt, tmpa); // A0 - xt mpc_sub(A0, yt, tmpb); // A0 - yt mpc_sub(A0, zt, tmpc); // A0 - yz mpc_sub(A0, pt, tmpd); // A0 - pt maxc4d(tmpa, tmpb, tmpc, tmpd, tmpa); // Max(?????) mpc_abs(tmpa, tmpaf); // |Max(?????)| mpf_mul(tmpcf, tmpaf, Q); // Q = (r / 4)^(-1 / 6) * |Max(?????)| m := 0; repeat mpc_sqrt(xt, sqrtx); // √x mpc_sqrt(yt, sqrty); // √y mpc_sqrt(zt, sqrtz); // √z mpc_sqrt(pt, sqrtp); // √p mpc_add(sqrty, sqrtz, tmpa); // √y + √z mpc_mul(tmpa, sqrtx, tmpb); // (√y + √z) * √x mpc_mul(sqrty, sqrtz, tmpc); // √y * √z mpc_add(tmpb, tmpc, lamda); // lamda = (√y + √z) * √x + √y * √z mpc_add(sqrtp, sqrtx, tmpa); // √p - √x mpc_add(sqrtp, sqrty, tmpb); // √p - √y mpc_add(sqrtp, sqrtz, tmpc); // √p - √z mpc_mul(tmpa, tmpb, tmpd); // (√p - √x)(√p - √y) mpc_mul(tmpd, tmpc, dm); // dm = (√p - √x)(√p - √y)(√p - √z) mpc_set_dbl(tmpa, -3 * m, 0); // (-3m, 0i) mpc_pow(d4, tmpa, p4); // 4^(-3m, 0i) mpc_abs(dm , tmpaf); if not s_mpf_is0(tmpaf) then begin // ゼロで除算回避 mpc_mul(p4, delta, tmpa); // 4^(-3m, 0i) * δ mpc_div(tmpa, dm, tmpb); // 4^(-3m, 0i) * δ / dm mpc_div(tmpb, dm, em); // em = 4^(-3m, 0i) * δ / dm / dm end else begin mpc_set_dbl(em, 2E200, 0); ERRF := ERRF or 16 + 2; end; mpc_add(one, em, tmpa); // 1 + em rcd(one, tmpa, tmpb); // rc(1, 1+ em) mpc_set_dbl(tmpc, -m, 0); // -m mpc_pow(d4, tmpc, p4); // 4^-m mpc_mul(p4, tmpb, tmpd); // 4^-m * rc(1 + em); if not s_mpf_is0(tmpaf) then begin // ゼロで除算回避 mpc_div(tmpd, dm, def); // def = 4^-m / dm * rc(1 + em) end else begin mpc_set_dbl(def, 1E200, 0); ERRF := ERRF or 16 + 4; end; mpc_add(sum, def, sum); // sum = sum + 4^-m / dm * rc(1 + em) mpc_add(Am, lamda, tmpd); // Am + lamda mpc_div(tmpd, d4, Am); // Am = (Am + lamda) / 4 mpc_add(xt, lamda, tmpd); // xt + lamda mpc_div(tmpd, d4, xt); // xt = (xt + lamda) / 4 mpc_add(yt, lamda, tmpd); // yt + lamda mpc_div(tmpd, d4, yt); // yt = (yt + lamda) / 4 mpc_add(zt, lamda, tmpd); // zt + lamda mpc_div(tmpd, d4, zt); // zt = (zt + lamda) / 4 mpc_add(pt, lamda, tmpd); // pt + lamda mpc_div(tmpd, d4, pt); // pt = (pt + lamda) / 4 m := m + 1; mpc_set_dbl(tmpa, -m, 0); // (-m, 0i) mpc_pow(d4, tmpa, p4); // 4^(-3m, 0i) mpc_abs(p4, tmpbf); // |4^(-3m, 0i)| mpf_mul(tmpbf, Q, tmpaf); // |4^(-3m, 0i)| * Q mpc_abs(Am, tmpcf); // |Am| until mpf_is_lt(tmpaf, tmpcf); // |4^(-3m, 0i)| * Q < |Am| mpc_set_dbl(tmpa, m, 0); // (m, 0i) mpc_pow(d4, tmpa, p4); // 4^(3m, 0i) mpc_mul(p4, Am, tmpd); // 4^(3m, 0i) * Am mpc_sub(A0, x, tmpb); // A0 - x mpc_div(tmpb, tmpd, X0); // X0 = (A0 - x) / 4^3m / Am mpc_sub(A0, y, tmpb); // A0 - y mpc_div(tmpb, tmpd, Y0); // Y0 = (A0 - y) / 4^3m / Am mpc_sub(A0, z, tmpb); // A0 - z mpc_div(tmpb, tmpd, Z0); // Z0 = (A0 - z) / 4^3m / Am mpc_chs(X0, tmpa); // -X0 mpc_sub(tmpa, Y0, tmpb); // -X0 - Y0 mpc_sub(tmpb, Z0, tmpc); // -X0 - Y0 - Z0 mpc_div(tmpc, d2, P0); // P0 = (-X0 - Y0 - Z0) / 2 mpc_sub(A0, y, tmpb); // A0 - y mpc_mul(X0, Y0, tmpa); // X0 * Y0 mpc_mul(X0, Z0, tmpb); // X0 * Z0 mpc_mul(Y0, Z0, tmpc); // Y0 * Z0 mpc_add(tmpa, tmpb, tmpd); // X0 * Y0 + X0 * Z0 mpc_add(tmpc, tmpd, tmpa); // X0 * Y0 + X0 * Z0 + Y0 * Z0 mpc_mul(P0, P0, tmpb); // P0 * p0 mpc_mul(tmpb, d3, tmpc); // 3 * P0 * p0 mpc_sub(tmpa, tmpc, E2); // E2 = X0 * Y0 + X0 * Z0 + Y0 * Z0 - 3 * P0 * p0 mpc_mul(X0, Y0, tmpa); // X0 * Y0 mpc_mul(tmpa, Z0, tmpb); // X0 * Y0 * Z0 mpc_mul(E2, P0, tmpa); // E2 * P0 mpc_mul(tmpa, d2, tmpc); // 2 * E2 * P0 mpc_mul(P0, P0, tmpa); // P0 * P0 mpc_mul(tmpa, P0, tmpd); // P0 * P0 * p0 mpc_mul(tmpd, d4, tmpa); // 4 * P0 * P0 * p0 mpc_add(tmpb, tmpc, tmpd); // X0 * Y0 * Z0 + 2 * E2 * P0 mpc_add(tmpd, tmpa, E3); // E3 = X0 * Y0 * Z0 + 2 * E2 * P0 + 4 * P0 * P0 * p0 mpc_abs(P0, Pm); // |P0| if not s_mpf_is0(Pm) then begin // |P0| <> 0 // 分母ゼロ回避 mpc_mul(P0, P0, tmpa); // P0 * P0 mpc_mul(tmpa, P0, tmpb); // tmpb P0 * P0 * P0 mpc_mul(tmpb, d3, tmpa); // tmpa 3 * P0 * P0 * P0 mpc_mul(E2, P0, tmpb); // tmpb E2 * P0 mpc_mul(X0, Y0, tmpc); // tmpc X0 * Y0 mpc_mul(tmpc, Z0, tmpd); // tmpd X0 * Y0 * Z0 mpc_mul(tmpd, d2, tmpc); // tmpc 2 * X0 * Y0 * Z0 mpc_add(tmpc, tmpb, tmpd); // tmpd = tmpc + tmpb 2 * X0 * Y0 * Z0 + E2 * P0 mpc_add(tmpd, tmpa, tmpb); // tmpb = tmpd + tmpa 2 * X0 * Y0 * Z0 + E2 * P0 + 3 * P0 * P0 * P0 mpc_div(tmpb, P0, E4); // E4 = tmpb / po 2 * X0 * Y0 * Z0 + E2 * P0 + 3 * P0 * P0 * P0 / P0 end else begin mpc_set_dbl(E4, 0, 0); // P0がゼロの時は誤差が小さくなっているで問題なし // ERRF := ERRF or 16 + 8; end; mpc_mul(X0, Y0, tmpa); // X0 * Y0 mpc_mul(tmpa, Z0, tmpb); // X0 * Y0 * Z0 mpc_mul(tmpb, P0, tmpc); // X0 * Y0 * Z0 * P0 mpc_mul(tmpc, P0, E5); // E5 = X0 * Y0 * Z0 * P0 * P0 mpc_set_dbl(tmpb, -m, 0); // -m, 0i mpc_pow(d4, tmpb, P4); // p4 = d4^-m mpc_set_dbl(tmpc, -3 / 2, 0); // -3 / 2, 0i mpc_pow(Am, tmpc, powa); // Am^(-3 / 2) mpc_mul(c1, E2, tmpa); // c1 * E2 mpc_sub(one, tmpa, def); // 1 - c1 * E2 mpc_mul(c2, E3, tmpb); // c2 * E3 mpc_add(def, tmpb, tmpc); // 1 - c1 * E2 + c2 * E3 mpc_mul(E2, E2, tmpb); // E2 * E2 mpc_mul(c3, tmpb, tmpd); // c3 * E2 * E2 mpc_add(tmpd, def, tmpa); // 1 - c1 * E2 + c2 * E3 + c3 * E2 * E2 mpc_mul(c4, E4, tmpb); // c4 * E4 mpc_mul(E2, E3, tmpc); // E2 * E3 mpc_mul(c5, tmpc, tmpd); // c5 * E2 * E3 mpc_sub(tmpa, tmpb, tmpc); // 1 - c1 * E2 + c2 * E3 + c3 * E2 * E2 - c4 * E4 mpc_sub(tmpc, tmpd, tmpa); // 1 - c1 * E2 + c2 * E3 + c3 * E2 * E2 - c4 * E4 - c5 * E2 * E3 mpc_mul(c6, E5, tmpb); // c6 * E5 mpc_add(tmpa, tmpb, def); // def = 1 - c1*E2 + c2*E3 + c3*E2*E2 - c4*E4 - c5*E2*E3 + c6*E5 mpc_mul(d6, sum, tmpa); // 6 * sum mpc_mul(powa, def, tmpb); // powa * def mpc_mul(tmpb, p4, tmpc); // d4^-m * powa * def mpc_add(tmpc, tmpa, rj); // rj = d4^-m * powa * def + 6 * sum if test < 0 then begin rfd(xt, yt, zt, tmpa); // rf(xt, yt, zt) mpc_sub(rcx, tmpa, tmpb); // rcx - rf(xt, yt, zt) mpc_mul(d3, tmpb, tmpc); // 3 * (rcx - rf(xt, yt, zt)) mpc_mul(b, rj, tmpd); // b * rj mpc_add(tmpc, tmpd, tmpa); // b * rj + 3 * (rcx - rf(xt, yt, zt)) mpc_mul(a, tmpa, rj); // rj = a * (b * rj + 3 * (rcx - rf(xt, yt, zt))) end; mpc_copy(rj, ans); EXT: mpc_clear(one); mpc_clear5(rj, xt, yt, zt, pt); mpc_clear5(sum, a, b, rho, A0); mpc_clear4(tau, rcx, lamda, Am); mpc_clear4(sqrtx, sqrty, sqrtz, sqrtp); mpc_clear3(dm, em, delta); mpc_clear3(c1, c2, c3); mpc_clear3(c4, c5, c6); mpc_clear4(X0, Y0, Z0, P0); mpc_clear4(E2, E3, E4, E5); mpc_clear5(d0, d2, d3, d4, d5); mpc_clear4(d6, p4, powa, def); mpc_clear4(tmpa, tmpb, tmpc, tmpd); mpf_clear3(tmpaf, tmpbf, tmpcf); mpf_clear2(Q, pm); end; // ---------------- Elliptic intehral Calc ------------------------------------- // 楕円積分計算 procedure TForm1.calc_Third_elliptic_integral_complex; label Ext; var kmax : double; c, mc, qc : mp_complex; rf0, rj0 : mp_complex; rft, rjt : mp_complex; afk, ek, fk, kc : mp_complex; tc1, tcm : mp_complex; tca, ac, one : mp_complex; tmpa, tmpb, d3 : mp_complex; tmpaf, tmpbf : mp_float; qmax : double; xc, ans : mp_complex; mdeg, ma, mk : mp_float; mq, mx, mm : mp_float; Intf : integer; k1x1F : boolean; a1x1F : boolean; // 第二種積分 procedure rinteg2(var ans: mp_complex); begin mpc_sub(c, one, tc1); // c - 1 mpc_sub(c, mc, tcm); // c - m RFd(tc1, tcm, c, rf0); RJd(tc1, tcm, c, c, rj0); mpc_mul(mc, rj0, tmpa); // m * rj mpc_div(tmpa, d3, tmpb); // m * rj / 3 mpc_sub(rf0, tmpb, ans); // ans = rf - rj / 3 end; // 第一三種積分 procedure rinteg3(ac: mp_complex; var ans: mp_complex); begin mpc_sub(c, one, tc1); // c - 1 mpc_sub(c, mc, tcm); // c - m mpc_sub(c, ac, tca); // c - a RFd(tc1, tcm, c, rf0); RJd(tc1, tcm, c, tca, rj0); mpc_mul(ac, rj0, tmpa); // a * rj mpc_div(tmpa, d3, tmpb); // a * rj / 3 mpc_add(rf0, tmpb, ans); // ans = rf + a * rj / 3 end; begin mpc_init3(c, mc, qc); mpc_init2(rf0, rj0); mpc_init2(rft, rjt); mpc_init3(afk, ek, fk); mpc_init2(tc1, tcm); mpc_init3(tca, ac, one); mpc_init3(tmpa, tmpb, d3); mpf_init3(tmpaf, tmpbf, mm); mpc_init3(xc, kc, ans); mpf_init5(mdeg, ma, mk, mq, mx); // データー入力 エラーが有ったら終了 if not datainput(ac, xc, kc) then goto Ext; ERRF := 0; ZeroF := 0; mpc_set_dbl(one, 1, 0); mpc_set_dbl(d3, 3, 0); mpc_mul(kc, kc, mc); mpf_set_int(tmpaf, 1); qmax := pi / 2; if mpf_is_gt(mc.re, tmpaf) then begin // パラメータm ,k が１より大きかったら mpf_copy(kc.re, tmpaf); // k mpf_inv(tmpaf, tmpbf); // 1/k mpf_arcsin(tmpbf, tmpaf); // sin^-1(1/k) qmax := abs(mpf_todouble(tmpaf)) end; Edit1.Text := '0'; Edit3.Text := '0'; Edit5.Text := '0'; Edit2.Text := ''; Edit4.Text := ''; Edit6.Text := ''; mpc_abs(xc, tmpbf); // |xc| // 積分範囲がゼロだったら終了 if s_mpf_is0(tmpbf) then goto Ext; kmax := 1 / sin(qmax); // 実数積分角度位置での最大離心率計算 Memo1.Clear; Memo1.Lines.Append('実数積分角度 = ' + floatTostr(qmax / pi * 180) + '°'); Memo1.Lines.Append('最大離心率 = ±' + floatTostr(kmax)); mpf_set1(tmpaf); if mpf_is_le(tmpbf, tmpaf) then begin mpc_inv(xc, tmpa); kmax := mpf_todouble(tmpa.re); Memo1.Lines.Append('指定角度の最大離心率 = ±' + floatTostr(kmax)); end; mpc_mul(xc, xc, tmpb); // xc^2 mpc_inv(tmpb, c); // c = 1 / xc^2 Intf := 0; // ∞フラグ mpf_abs(xc.re, tmpaf); mpf_abs(kc.re, tmpbf); // x = 1 k = 1 check フラグセット if mpf_is1(tmpaf) and mpf_is0(xc.im) and mpf_is1(tmpbf) and mpf_is0(kc.im) then k1x1F := true else k1x1F := False; // x = 1 a = 1 check フラグセット if mpf_is1(tmpaf) and mpf_is0(xc.im) and mpf_is1(ac.re) and mpf_is0(ac.im) then a1x1F := true else a1x1F := False; if k1x1f or a1x1f then begin mpc_set_dbl(afk, maxdouble, 0); // 第三種∞ Intf := Intf or 1; end else begin rinteg3(ac, afk); // 第三種積分 end; mpf_copy(afk.im, tmpaf); // 虚数部が1E-55より小さかったら0に mpf_abs(tmpaf, tmpbf); mpf_set_dbl(tmpaf, 1E-55); if mpf_is_lt(tmpbf, tmpaf) then mpf_set0(afk.im); if not s_mpf_is_ge0(xc.re) then mpc_chs(afk, afk); // 積分範囲が-だったら符号反転 if Intf and 1 = 0 then Edit1.Text := string(mpf_decimal_alt(afk.re, 50)) // 第三種 実数部出力 else begin if s_mpf_is_ge0(xc.re) then Edit1.Text := '∞' else Edit1.Text := '-∞'; end; if k1x1F then begin // k = 1 and x = 1 mpc_set_dbl(ek, 1, 0); // 第二種 1 end else begin rinteg2(ek); // 第二種積分 end; mpf_copy(ek.im, tmpaf); // 虚数部が1E-55より小さかったら0に mpf_abs(tmpaf, tmpbf); mpf_set_dbl(tmpaf, 1E-55); if mpf_is_lt(tmpbf, tmpaf) then mpf_set0(ek.im); if not s_mpf_is_ge0(xc.re) then mpc_chs(ek, ek); // 積分範囲が-だったら符号反転 Edit3.Text := string(mpf_decimal_alt(ek.re, 50)); // 第二種種 実数部出力 if k1x1F then begin // k = 1 and x = 1 mpc_set_dbl(fk, maxdouble, 0); // 第一種∞ Intf := Intf or 2; end else begin mpc_set_dbl(ac, 0, 0); // acにゼロセット rinteg3(ac, fk); // 第一種積分 end; mpf_copy(fk.im, tmpaf); // 虚数部が1E-55より小さかったら0に mpf_abs(tmpaf, tmpbf); mpf_set_dbl(tmpaf, 1E-55); if mpf_is_lt(tmpbf, tmpaf) then mpf_set0(fk.im); if not s_mpf_is_ge0(xc.re) then mpc_chs(fk, fk); // 積分範囲が-だったら符号反転 if Intf and 2 = 0 then Edit5.Text := string(mpf_decimal_alt(fk.re, 50)) // 第一種 実数部出力 else begin if s_mpf_is_ge0(xc.re) then Edit5.Text := '∞' else Edit5.Text := '-∞'; end; if Intf and 1 = 0 then Edit2.Text := string(mpf_decimal_alt(afk.im, 50) + 'i'); // 第三種 虚数部出力 Edit4.Text := string(mpf_decimal_alt(ek.im, 50) + 'i'); // 第二種 虚数部出力 if Intf and 2 = 0 then Edit6.Text := string(mpf_decimal_alt(fk.im, 50) + 'i'); // 第一種 虚数部出力 if ERRF <> 0 then Form1.Memo1.Lines.Append('RJ ゼロでの除算あり code=' + intTostr(ERRF)); if ZeroF and 1 <> 0 then Memo1.Lines.Text := Memo1.Lines.Text + (#13#10 + 'RCで 引数 y=0 がありました。'); if ZeroF and 2 <> 0 then Memo1.Lines.Text := Memo1.Lines.Text + (#13#10 + 'RFで 引数 ゼロが二個 がありました。'); if ZeroF and 4 <> 0 then Memo1.Lines.Text := Memo1.Lines.Text + (#13#10 + 'RJで 引数 ゼロが二個 がありました。'); Ext: mpc_clear3(c, mc, qc); mpc_clear2(rf0, rj0); mpc_clear2(rft, rjt); mpc_clear3(afk, ek, fk); mpc_clear2(tc1, tcm); mpc_clear3(tca, ac, one); mpc_clear3(tmpa, tmpb, d3); mpf_clear3(tmpaf, tmpbf, mm); mpc_clear3(xc, kc, ans); mpf_clear5(mdeg, ma, mk, mq, mx); end; // ---------------- 入力処理 --------------------------------------------------- var XF: boolean; // 角度入力、範囲入力 選択フラグ // データの入力 // ac 第三種楕円積分特性値 n // xc 積分範囲 // kc 離心率 function TForm1.datainput(var ac, xc, kc: mp_complex): boolean; label Ext; var FI : boolean; ch, l : integer; a, k, degr, degi : double; m : double; qc : mp_complex; kstr, kss : string; c : char; mdeg, mdegi, tmpaf, tmpbf : mp_float; mq, mk, mx, ma : mp_float; begin result := False; FI := False; val(LabeledEdit1.Text, a, ch); if ch <> 0 then begin application.MessageBox('a(特性)の値に間違いがあります。','a(特性)',0); exit; end; val(LabeledEdit2.Text, degr, ch); if ch <> 0 then begin application.MessageBox('φ(deg)の値に間違いがあります。','φ(deg)',0); exit; end; if abs(degr) > 90 then begin application.MessageBox('φ(deg)の絶対値値は90°迄です。','φ(deg)',0); exit; end; val(LabeledEdit5.Text, degi, ch); if ch <> 0 then begin application.MessageBox('φ(deg)iの値に間違いがあります。','φ(deg)',0); exit; end; if (abs(degr) < 90) and (degi <> 0) then begin application.MessageBox('φ(deg)が90°以下の場合φ(deg)iの値はゼロです。','φ(deg)',0); exit; end; if (degr * degi > 0) and (abs(degr) >= 90) then begin application.MessageBox('φ(deg)とφ(deg)iの符号は±を逆にして下さい','φ(deg)',0); exit; end; if radiobutton1.Checked = true then begin kstr := LabeledEdit3.Text; l := length(kstr); // 文字の長さ取得 c := kstr[l]; // iの文字確認 if (c = 'i') or (c = 'I') then begin // i虚数指定だったら kss := copy(kstr, 1, l - 1); // iの前までコピー FI := true; // 虚数フラグセット end else Kss := kstr; val(kss, k, ch); // kss 数値確認 if ch <> 0 then begin application.MessageBox('k(離心率)の値に間違いがあります。','k(離心率)',0); exit; end; end; if radiobutton2.Checked = true then begin val(LabeledEdit6.Text, m, ch); if ch <> 0 then begin application.MessageBox('ｍの値に間違いがあります。','m=k^2',0); exit; end; if m < 0 then FI := true; // 虚数フラグセット end; mpc_init(qc); mpf_init4(mdeg, mdegi, tmpaf, tmpbf); mpf_init4(mq, mx, mk, ma); mpf_set0(tmpaf); mpf_read_decimal(ma, PAnsiChar(ansistring(LabeledEdit1.Text + #00))); // a mpc_set_mpf(ac, ma, tmpaf); if radiobutton2.Checked = true then begin mpf_read_decimal(mk, PAnsiChar(ansistring(LabeledEdit6.Text + #00))); // m mpf_abs(mk, mk); // |m| mpf_sqrt(mk, mk); // √m end; if radiobutton1.Checked = true then begin mpf_read_decimal(mk, PAnsiChar(ansistring(kss))); // k string -> mk mp_float end; if FI then mpc_set_mpf(kc, tmpaf, mk) // 虚数だったら kc=(0, mki) else mpc_set_mpf(kc, mk, tmpaf); // 実数だったら kc=(mk, 0i) if not XF then begin mpf_read_decimal(mdeg, PAnsiChar(ansistring(LabeledEdit2.Text + #00))); mpf_div_dbl(mdeg, 180, tmpaf); // mdeg / 180 mpf_set_pi(tmpbf); // pi mpf_mul(tmpaf, tmpbf, mdeg); // mdeg = mdeg / 180 * pi mpf_read_decimal(mdegi, PAnsiChar(ansistring(LabeledEdit5.Text + #00))); mpf_div_dbl(mdegi, 180, tmpaf); // degi / 180 mpf_mul(tmpaf, tmpbf, mdegi); // mdegi = mdei / 180 * pi mpc_set_mpf(qc, mdeg, mdegi); mpc_sin(qc, xc); // sin(qc) LabeledEdit4.Text:= string(mpf_decimal_alt(xc.re, 50)); mpf_set0(xc.im); end else begin mpf_read_decimal(mx, PAnsiChar(ansistring(LabeledEdit4.Text + #00))); mpf_set0(tmpaf); mpc_set_mpf(xc, mx, tmpaf); end; result := true; mpc_clear(qc); mpf_clear4(mdeg, mdegi, tmpaf, tmpbf); mpf_clear4(mq, mx, mk, ma); end; // 角度入力 procedure TForm1.Button1Click(Sender: TObject); begin Button1.Enabled := False; XF := False; calc_Third_elliptic_integral_complex; Button1.Enabled := True; end; // Xの値入力 procedure TForm1.Button2Click(Sender: TObject); var x : double; ch : integer; mx , tmpaf, tmpbf: mp_float; mxc, mcq : mp_complex; begin val(LabeledEdit4.Text, x, ch); if ch <> 0 then begin application.MessageBox('Xの値に間違いがあります。','X',0); exit; end; Button2.Enabled := False; mpf_init3(mx, tmpaf, tmpbf); mpc_init2(mxc, mcq); XF := True; mpf_read_decimal(mx, PAnsiChar(ansistring(LabeledEdit4.Text + #00))); mpf_set0(tmpaf); mpc_set_mpf(mxc, mx, tmpaf); mpc_arcsin(mxc, mcq); mpf_set_pi(tmpaf); mpf_div(mcq.re, tmpaf, tmpbf); // xc.re / pi mpf_mul_dbl(tmpbf, 180, mx); // xc.re / pi * 180 LabeledEdit2.Text:= string(mpf_decimal_alt(mx, 50)); mpf_div(mcq.im, tmpaf, tmpbf); // xc.re / pi mpf_mul_dbl(tmpbf, 180, mx); // xc.re / pi * 180 LabeledEdit5.Text:= string(mpf_decimal_alt(mx, 50)); calc_Third_elliptic_integral_complex; mpf_clear3(mx, tmpaf, tmpbf); mpc_clear2(mxc, mcq); Button2.Enabled := True; end; end.
elliptic_integral_complex.zip
各種プログラム計算例に戻る