ランデン変換による第一二種楕円積分
１．離心率Ｋが１以上でも虚数部のない計算
ランデン変換による楕円積分は、楕円の周長で取り上げていますが、楕円積分の離心率関連のパラメーターの範囲が狭かったので改めて追加しました。
複素数の楕円積分との比較の為でもあります。
プログラムは、Mathematics Source Library C & ASM にあるランデン変換のプログラムをＤｅｌｐｈｉ用にしたものです。
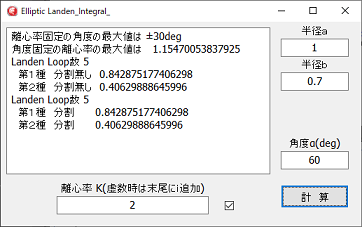離心率ｋに入力の制限はありません、虚数を入力する場合は、数字の末尾に ｉ を付加します。(例 0.7i)
虚数の入力によりパラメーターｍ (ｍ＝ｋ＾２)の値にマイナスの値を指定できます。
角度の値は実数のみですが大さには制限があのません。
複素数を使用していないので、虚数部の計算はありません。
離心率に１より大きい値を指定にすると、虚数の積分範囲が発生しますが、この値は計算されません。
９０°以上の場合、実数部分だけが積分され、１８０°を指定すると、９０°の倍の値になります。
半径指定による離心率ｋの計算は、実数の計算のみで虚数の入力は出来ません。
プログラム
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.Buttons, Vcl.ExtCtrls;
type
TForm1 = class(TForm)
parameter_k_Edit: TLabeledEdit;
arc_degree_Edit: TLabeledEdit;
BitBtn1: TBitBtn;
Memo1: TMemo;
radius_a_Edit: TLabeledEdit;
radius_b_Edit: TLabeledEdit;
CheckBox1: TCheckBox;
procedure FormCreate(Sender: TObject);
procedure BitBtn1Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses system.Math;
var
LDBL_EPSILON: extended;
//------------------------------------------------------------------------------
// ランデン変換楕円積分 第一種第二種
function Landen_Transform(phi, parameter: extended; var F, Fk, E, Ek: extended): integer;
var
two_n: extended;
a, g, a_old, g_old: extended;
tan_2n_phi, sum, integral: extended;
n : integer;
begin
two_n := 1.0;
a := 1.0;
g := sqrt(1.0 - parameter);
sum := 2.0 * (2.0 - parameter);
integral := 0.0;
n := 0;
repeat
tan_2n_phi := tan(two_n * phi); // tan(90°) = -3.68934 E19 無限大になりません
sum := sum - two_n * (a - g) * (a - g);
two_n := two_n + two_n;
phi := phi - arctan((a - g) * tan_2n_phi / (a + g * tan_2n_phi * tan_2n_phi)) / two_n;
integral := integral + (a - g) * sin(two_n * phi);
g_old := g;
a_old := a;
a := (g_old + a_old) / 2;
g := sqrt(g_old * a_old);
inc(n);
until (abs(a_old - g_old) <= (a_old * LDBL_EPSILON));
F := phi / g;
Fk := PI / 2 / g;
E := 1 / 2 * integral + 1 / 4 * sum * phi / g;
Ek := PI / 8 / a * sum;
result := n;
end;
//------------------------------------------------------------------------------
// 離心率ｋの値が１より大きい場合の計算
// 正しい答えがでる角度の最大値があるので注意が必要です。
// GF フラグ true で分割なし計算
// 虚数部分はありません
function Large_Modulus_prus(phi, ki: extended; var F, K, E, Ek: extended; GF: boolean): integer;
var
m : extended;
sin_phi: extended;
n : integer;
signphi : integer;
begin
signphi := sign(phi);
m := ki * ki;
phi := abs(phi);
n := trunc((phi + PI / 2 )/ PI);
phi := phi - n * PI;
n := n + n;
sin_phi := sin(phi);
if abs(sin_phi) >= 1.0 / ki then begin // 実数積分範囲を越えたら90°+ n * 90迄計算
if phi > 0.0 then phi := PI / 2 // 虚数部分は計算されません
else phi := - PI/ 2;
end
else phi := arcsin(ki * sin_phi);
if GF then begin
result := Landen_Transform(abs(phi + n * pi / 2), 1 / m, F, K, E, Ek);
E := E * ki + (1.0 - m) * F / ki;
F := F / ki;
E := E * signphi;
F := F * signphi;
exit;
end;
result := Landen_Transform(abs(phi), 1 / m, F, K, E, Ek);
Ek := ki * Ek + (1.0 - m) * K / ki;
E := ki * E + (1.0 - m) * F / ki;
if phi >= 0.0 then begin
F := F + n * K;
E := E + n * Ek;
end
else begin
F := n * K - F;
E := n * Ek - E;
end;
F := F / ki * signphi;
E := E * signphi;
end;
// 離心率ｋの値がＫ＞１の場合の計算
// 正しい答えの出る角度と離心率表示
procedure Large_Modulus_prus_k(phiin, kin: extended);
var
F, E: extended;
K, EK: extended;
i: integer;
degmax, kmax: extended;
begin
degmax := arcsin(sqrt(1 / (kin * kin))) / pi * 180;
kmax := sin(phiin);
if kmax <> 0 then begin
kmax := sqrt(1 / (kmax * kmax));
Form1.Memo1.Lines.Append('離心率固定の角度の最大値は ±' + floatTostr(degmax) + 'deg');
Form1.Memo1.Lines.Append('角度固定の離心率の最大値は ' + floatTostr(kmax));
end;
i := Large_Modulus_prus(phiin, kin, F, K, E, Ek, True);
Form1.Memo1.Lines.Append('Landen Loop数 ' + intTostr(i));
Form1.Memo1.Lines.Append(' 第１種 分割無し ' + floatTostr(F));
Form1.Memo1.Lines.Append(' 第２種 分割無し ' + floatTostr(E));
i := Large_Modulus_prus(phiin, kin, F, K, E, Ek, False);
Form1.Memo1.Lines.Append('Landen Loop数 ' + intTostr(i));
Form1.Memo1.Lines.Append(' 第１種 分割 ' + floatTostr(F));
Form1.Memo1.Lines.Append(' 第２種 分割 ' + floatTostr(E));
end;
//------------------------------------------------------------------------------
// パラメータmの値がマイナスの時の計算
// GF フラグ true で分割なし計算
function Elliptic_Integrals(phi, m: extended; var F, K, E, Em: extended; GF: boolean): integer;
var
n: integer;
pai, pis2: extended;
begin
if GF then begin
result := Landen_Transform(abs(phi), m, F, K, E, Em);
exit;
end;
pai := pi;
pis2 := pi / 2;
n := trunc((phi + pis2) / pai);
phi := phi - n * pai;
n := n + n;
result := Landen_Transform(abs(phi), m, F, K, E, Em);
if phi >= 0.0 then begin
F := F + n * K;
E := E + n * Em;
end
else begin
F := n * K - F;
E := n * Em - E;
end;
end;
// パラメータｍの値がｍ＜０の時の計算
procedure Elliptic_Integral_minus_m(phiin, m: extended);
var
F, E: extended;
K, EK : extended;
dum : extended;
signphi : extended;
phi : extended;
i : integer;
begin
signphi := sign(phiin);
phi := PI / 2 - abs(phiin);
i := Elliptic_Integrals(phi, abs(m / (1.0 - m)), F, K, E, Ek, True);
dum := sqrt(1.0 - m);
if abs(phiin) > pi / 2 then begin
F := signphi * (F + K) / dum;
E := signphi * (E + EK) * dum;
end
else begin
F := signphi * (K - F) / dum;
E := signphi * (EK - E) * dum;
end;
K := K / dum;
Ek:= Ek * dum;
Form1.Memo1.Lines.Append('Landen Loop数 ' + intTostr(i));
Form1.Memo1.Lines.Append(' 第１種 分割無し ' + floatTostr(F));
Form1.Memo1.Lines.Append(' 第２種 分割無し ' + floatTostr(E));
i := Elliptic_Integrals(phi, abs(m / (1.0 - m)), F, K, E, Ek, False);
Form1.Memo1.Lines.Append('Landen Loop数 ' + intTostr(i));
F := signphi * (K - F) / dum;
E := signphi * (EK - E) * dum;
K := K / dum;
Ek:= Ek * dum;
Form1.Memo1.Lines.Append(' 第１種 90°分割 ' + floatTostr(F));
Form1.Memo1.Lines.Append(' 第２種 90°分割 ' + floatTostr(E));
end;
//------------------------------------------------------------------------------
// パラメータｍの値が ｍ＞＝１の時の計算
procedure Elliptic_Integral_FS(phi, m: extended);
var
n, i: integer;
F, K, E, Ek: extended;
begin
if m = 1.0 then begin
if abs(phi) >= PI / 2 then begin
F := infinity;
if phi < 0 then F := -F;
end
else begin
K := tan(Phi);
F := sign(Phi) * ln(abs(K) + sqrt(1.0 + K * K));
end;
if (abs(phi) <= PI / 2) then begin
E := sin(phi);
end
else begin
n := trunc((abs(phi) + PI / 2) / PI);
E := n + n + sin(abs(phi) - n * PI);
if phi < 0 then E := - E;
end;
K := infinity;
EK := 1;
Form1.Memo1.Lines.Append(' 第１種 m = 1 ' + floatTostr(F));
Form1.Memo1.Lines.Append(' 第２種 m = 1 ' + floatTostr(E));
exit;
end;
// 分割無し計算
i := Landen_Transform(abs(phi), m, F, K, E, Ek);
Form1.Memo1.Lines.Append('Landen Loop数 ' + intTostr(i));
F := sign(phi) * F;
E := sign(phi) * E;
Form1.Memo1.Lines.Append(' 第１種 分割無し ' + floatTostr(F));
Form1.Memo1.Lines.Append(' 第２種 分割無し ' + floatTostr(E));
// 90°分割計算
n := trunc((phi + PI / 2) / PI);
phi := phi - n * PI;
n := n + n;
i := Landen_Transform(abs(phi), m, F, K, E, Ek);
Form1.Memo1.Lines.Append('Landen Loop数 ' + intTostr(i));
F := sign(phi) * F + n * K;
E := sign(phi) * E + n * Ek;
Form1.Memo1.Lines.Append(' 第１種 90°分割 ' + floatTostr(F));
Form1.Memo1.Lines.Append(' 第２種 90°分割 ' + floatTostr(E));
end;
//------------------------------------------------------------------------------
procedure TForm1.BitBtn1Click(Sender: TObject);
var
kin, m : extended;
a, b : extended;
deg, phi : extended;
ch,l : integer;
kstr, kss : string;
c : char;
kssF : boolean;
begin
val(radius_a_edit.Text, a, ch);
if ch <> 0 then begin
application.MessageBox('半径aの値に間違いがあります。','注意',0);
exit;
end;
if a <= 0 then begin
application.MessageBox('半径aの値は０より大きくして下さい。','注意',0);
exit;
end;
val(radius_b_edit.Text, b, ch);
if ch <> 0 then begin
application.MessageBox('半径bの値に間違いがあります。','注意',0);
exit;
end;
if b < 0 then begin
application.MessageBox('半径ｂの値は０以上にして下さい。','注意',0);
exit;
end;
val(arc_degree_edit.Text, deg, ch);
if ch <> 0 then begin
application.MessageBox('積分の範囲αの値に間違いがあります。','注意',0);
exit;
end;
memo1.Clear;
kssF := False;
if checkbox1.Checked then begin // k指定計算
kstr := parameter_k_edit.Text;
if kstr = '' then begin
application.MessageBox('離心率kの値がありません。','注意',0);
exit;
end;
l := length(kstr); // 文字の長さ
c := kstr[l]; // 最後の文字取得
if (c = 'i') or (c = 'I') then begin // i だったら虚数
kssF := True; // 虚数フラグセット
kss := copy(kstr,1, l - 1); // iの前までコピー
end
else Kss := kstr;
val(Kss, kin, ch);
if ch <> 0 then begin
application.MessageBox('離心率kの値に間違いがあります。','注意',0);
exit;
end;
m := kin * kin; // k^2
if kssF then m := -m; // 虚数指定だったらm -> -m
end
else begin // k指定で無かったら
m := 1 - b * b / a / a; // m = (a^2-b^2)/a^2 k = √m
kin := sqrt(abs(m));
if m >= 0 then
parameter_k_edit.Text := floatTostr(kin)
else
parameter_k_edit.Text := floatTostr(kin) + 'i';
end;
phi := deg / 180 * pi;
if (m >= 0) and (m <= 1) then begin // 0 <= m <=1 -1 <= K <= 1
Elliptic_Integral_FS(phi,m);
end;
if m < 0 then begin // m < 0 k > 0i
Elliptic_Integral_minus_m(phi, m);
end;
if m > 1 then begin // m > 1 k > 1 or k < -1
kin := sqrt(m);
Large_Modulus_prus_k(phi, kin);
end;
end;
//------------------------------------------------------------------------------
// 初期設定
procedure TForm1.FormCreate(Sender: TObject);
var
one, tmp: extended;
begin
one := 1;
LDBL_EPSILON := one;
repeat
LDBL_EPSILON := LDBL_EPSILON / 2;
tmp := LDBL_EPSILON + one;
until tmp = one;
LDBL_EPSILON := LDBL_EPSILON * 2; // extended LDBL_EPSILON := 2^(1-64)
memo1.Clear;
memo1.Lines.Append('第１種、第２種楕円積分');
end;
end.
２．Ｋ離心率が１以上の場合は、虚数部のある計算
Mathematics Source Library C & ASM にあるランデン変換では、計算途中に、関数ｔａｎ()の計算があり、複素数の計算時、分母がゼロになる計算が発生するのと同時に計算誤差が大きい為、配列によるランデン変換の計算を複素数の計算に変更して計算出来るようにしました。
複素数の計算に、ｄｅｌｐｈｉ標準のＶａｒｉａｎｔ変数を使用すると、桁落ちが発生するルーチンには、多倍長と、ｄｏｕｂｌｅの複素数の計算を採用しました。
全てを多倍長で計算すれば良かったのですが、全て多倍長にしてしまうと、プログラムを読みづらくなるのと、手間がかかるので、部分的にしました。
多倍長の組み込みは
MPArithからmparith_2018-11-27.zipをダウンロードします。
ファイルの日付が変わるので、変わっていたら新しいのをダウンロードして下さい。
Zipファイルを解凍して、解凍したフォルダーにパス(ツール->オプション->Delphiオプション->ライブラリ->ライブラリパス)を追加し、Uses に mp_types, mp_real, mp_cmplx, mp_baseを追加すれば使用可能になります。
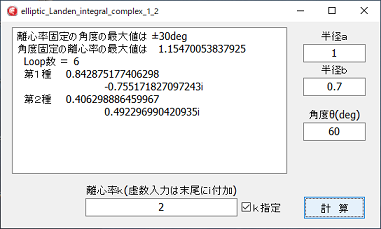計算は、ｋ離心率の値が１を越えた場合のランデン変換計算だけ、複素数の計算をしています。
離心率の値が１以下の場合は、実数のみで ｄｏｕｂｌｅの精度の計算です。
複素数のランデン変換のルーチンは、積分角度が９０°を越える場合９０°象限分割方式でないと計算出来ないので、実数のランデン変換も同じ方法としました。
実数のランデン変換を使用せず、複素数のランデン変換だけでも計算は可能です。
実際に複素数が必要なのは、離心率ｋの値が１以上の値を処理する Large_Modulus_prus_complex ルーチンの
phi := VarComplexarcsin(ki * sin_phi);
の行からです。
複素数の逆ｓｉｎ関数の引数が１より大きくなると、複素数の角度に虚数が値の値が発生します。
積分範囲の指定に楕円の中心に対する角度として指定する方法と、ｓｉｎ-1（ｘ）の ｘ の値を指定する場合があります。
ｘ の値を指定した場合、±１を越える部分は、全て虚数の角度となります。
積分範囲を角度で指定した場合で、90°を越えて指定した場合は、一般的には楕円の中心に対する角度の指定として計算していますので90°単位の象限分割計算となります。
計算によっては、90°を越えても、ｓｉｎ（角度）として、±１ の範囲の計算としている場合もありますので注意が必要です。
プログラム
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.Buttons, Vcl.ExtCtrls;
type
TForm1 = class(TForm)
radius_a_Edit: TLabeledEdit;
radius_b_edit: TLabeledEdit;
arc_degree_edit: TLabeledEdit;
BitBtn1: TBitBtn;
Memo1: TMemo;
k_Edit: TLabeledEdit;
CheckBox1: TCheckBox;
procedure BitBtn1Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses system.Math, System.VarCmplx, mp_real, mp_cmplx, mp_types, mp_base;
var
LDBL_EPSILON: double;
// 複素数構造体
type
TCdouble = record
r : double;
i : double;
end;
// 複素数変換 Varint to TCdouble
function VtoT(x : variant): TCdouble;
begin
result.r := x.real;
result.i := x.Imaginary;
end;
// 複素数変換 TCdouble to variant;
function TtoV(x : TCdouble): variant;
begin
result := varascomplex(result);
result.real := x.r;
result.Imaginary := x.i;
end;
// TCdouble複素数の除算
function cdiv(a, b: TCdouble): TCdouble;
var
bb: double;
begin
result.r := 0;
result.i := 0;
bb := b.r * b.r + b.i * b.i;
if bb <> 0 then begin
result.r := (a.r * b.r + a.i * b.i) / bb;
result.i := (a.i * b.r - a.r * b.i) / bb;
end;
end;
// 複素数の生成
function Varcomplex(a, b: double): Variant;
begin
result := varascomplex(result);
result.real := a;
result.Imaginary := b;
end;
//--------------------------------------------------------------------------------------------------
// 第１種第２種不完全楕円積分 Large_Modulus_prus_complex 専用
// FBnKn[0] 第１種楕円積分解
// EBnKn[0] 第２種楕円積分解
// ランデン変換
// Q 角度 rad
// m = k^2
// 虚数部の値が必要なので複素数の計算をします。
// このルーチンもランデン変換ですが、tanの計算が無く桁落ちが発生しずらいので採用しています。
// 90°(pi/2)以上は90°分割計算が必要です。
//--------------------------------------------------------------------------------------------------
function second_imperfect_elliptic_integral(Q, m: variant; var F, E: variant): integer;
var
I, MI : integer;
k : double;
Kn : array of double; // Kn
knd : array of variant; // k'n
N2SKn : array of variant; // 2/(1+Kn)
T2SKnd : array of variant; // П2/(1+Kn')
BRad : array of variant; // β(rad)
SinBn : array of variant; // sinβn
FBnKn : array of variant; // F(βn,kn)
EBnKn : array of variant; // E(βn,kn)
mtmp0, mtmp1 : mp_complex;
tmp0 : variant;
LnD : variant;
mpt0, mpt1 : TCdouble;
begin
mpc_init2(mtmp0, mtmp1);
k := sqrt(m.real);
MI := 0;
LND := 0;
setlength(kn, MI + 1); // kn
kn[0] := K;
while LND <> Kn[MI] do begin
LnD := Kn[MI];
inc(MI);
setlength(kn, MI + 1); // kn
kn[MI] := 2 * sqrt(Kn[MI - 1])/(1 + Kn[MI - 1]);
end;
Dec(MI);
setlength(kn, MI + 1); // kn
setlength(knd, MI + 1); // k'n
setlength(N2SKn, MI + 1); // 2/(1+Kn)
setlength(T2SKnd, MI + 1); // П2/(1+Kn')
setlength(BRad, MI + 1); // β(rad)
setlength(SinBn, MI + 1); // sinβn
setlength(FBnKn, MI + 1); // F(βn,kn)
setlength(EBnKn, MI + 1); // E(βn,kn)
knd[0] := Varcomplex(1, 0);
for I := 1 to MI do
knd[I] := Varcomplex((1 - kn[I - 1]) / (1 + Kn[I - 1]), 0);
for I := 0 to MI do
N2SKn[I] := Varcomplex(2 / (1 + kn[I]), 0);
T2SKnd[MI] := N2SKn[MI];
for I := MI - 1 downto 0 do
T2SKnd[I] := T2SKnd[I + 1] * N2SKn[I];
BRad[0] := Q;
for I := 1 to MI do
BRad[I] := (Varcomplexarcsin(kn[I - 1] * Varcomplexsin(Brad[I - 1])) + Brad[I - 1]) / 2;
for I := 0 to MI do
SinBn[I] := Varcomplexsin(Brad[I]);
// ゼロで除算防止 Varcomplexcos(Brad[MI]) だと積分角度が270°で桁落ちにより 0 になります
mpc_set_dbl(mtmp0, Brad[MI].real, Brad[MI].Imaginary); // variant -> mpc
mpc_cos(mtmp0, mtmp1); // 多倍長複素数cos
mpt0.r := mpf_todouble(mtmp1.re); // mpc.re -> TCdouble.r
mpt0.i := mpf_todouble(mtmp1.im); // mpc.im -> TCdouble.i
tmp0 := 1 + Varcomplexsin(Brad[MI]);
mpt1 := VtoT(tmp0); // variant -> TCdouble
mpt0 := cdiv(mpt1, mpt0); // (1 + Varcomplexsin(Brad[MI])) / Varcomplexcos(Brad[MI]);
mpc_set_dbl(mtmp0, mpt0.r, mpt0.i); // TCdouble -> mpc_complex
mpc_ln(mtmp0, mtmp1); // ln((1+sin(Brad[MI]))/ cos(brad[MI])
Lnd := Varcomplex(0, 0);
LnD.real := mpf_todouble(mtmp1.re); // mpc_coplex->variant
LnD.Imaginary := mpf_todouble(mtmp1.im);
for I := 0 to MI do
FBnKn[I] := T2SKnd[I] * LnD;
F := FBnKn[0];
mpc_set_dbl(mtmp0, Brad[MI].real, Brad[MI].Imaginary); // variant -> mpc
mpc_sin(mtmp0, mtmp1); // 多倍長複素数sin
EBnKn[MI] := Varcomplex(0, 0);
EBnKn[MI].real := mpf_todouble(mtmp1.re);
EBnKn[MI].Imaginary := mpf_todouble(mtmp1.im);
// EBnKn[MI] := Varcomplexsin(Brad[MI]);
for I := MI - 1 downto 0 do
EBnKn[I] := (2 * EBnKn[I + 1] + 2 * knd[I + 1] * FBnKn[I + 1]) / (1 + knd[I + 1]) - kn[I] * SinBn[I];
E := EBnKn[0];
result := MI + 1;
mpc_clear2(mtmp0, mtmp1);
end;
//--------------------------------------------------------------------------------------------------
// 離心率 ｋの値が Ｋ＞１の場合の複素数計算。
// 分割角度角度90°分割計算。
// 虚数部があり非分割での計算不可。
// ｋ離心率の値が１を超えると、双曲線となり虚数部が発生します。
//--------------------------------------------------------------------------------------------------
function Large_Modulus_prus_complex(phi, ki: variant; var F, E: variant): integer;
var
one : variant;
m : variant;
sin_phi : variant;
Fk, Ek : variant;
n, nn : integer;
signphi : integer;
signp : integer;
mm : variant;
phib : variant;
pai : double;
l1, l2 : integer;
begin
m := varascomplex(m);
mm := varascomplex(mm);
sin_phi := varascomplex(sin_phi);
one := Varcomplex(1, 0); // one = 1 + 0i
pai := PI; // πextended -> double;
signphi := sign(phi.real); // 角度の符号取得
m := ki * ki; // m = k^2
// 象限の積分
phi.real := abs(phi.real); // 角度の絶対値
n := trunc((phi.real + pai / 2 ) / pai); // 積分角度 90度の倍数
phi := phi - n * pai; // 象限の積分角度
signp := sign(phi.real);
sin_phi := VarComplexSin(phi); // sin(象限の積分角度)
phi := VarComplexarcsin(ki * sin_phi); // 離心率k>1によるd象限の積分角
nn := n + n; // nn = 2n
mm := VarComplexInverse(m); // mm := 1/m
// pai := VarComplexAngle(phi); // 複素数平面角度
// Form1.Memo1.Lines.Append('複素数平面角度 = ' + floatTostr(pai / pi * 180));
if phi.real < 0 then phi := -phi; // phi.real > 0 に設定
l1 := second_imperfect_elliptic_integral(phi, mm, F, E); // ランデン変換積分
// 90°の積分
phib := varcomplex(pai / 2, 0 ); // 積分角度90°
sin_phi := varcomplexsin(phib);
phib := VarComplexarcsin(ki * sin_phi); // 離心率 k > 1 によるの積分角
l2 := second_imperfect_elliptic_integral(phib, mm, Fk, Ek); // ランデン変換積分90°
EK := ki * EK + (one - m) * FK / Ki;
E := ki * E + (one - m) * F / Ki;
// 奇数偶数象限による計算
if signp > 0 then begin
F := F + nn * FK;
E := E + nn * EK;
end
else begin
F := nn * FK - F;
E := nn * EK - E;
end;
F := F / ki;
E := E * signphi; // 積分角度の方向で符号設定
F := F * signphi;
result := max(l1, l2); // ループ数
end;
//--------------------------------------------------------------------------------------------------
// ランデン変換楕円積分 第一種第二種 完全 不完全 実数計算
// m < 1
// 第一種第二種楕円積分と完全と不完全積分が同時に行なわれます。
// 積分角度の上限はありません。
//--------------------------------------------------------------------------------------------------
function Landen_Transform(phi, parameter: double; var F, Fk, E, Ek: double): integer;
var
two_n: double;
a, g, a_old, g_old: double;
tan_2n_phi, sum, integral: double;
n : integer;
begin
two_n := 1.0;
a := 1.0;
g := sqrt(1.0 - parameter);
sum := 2.0 * (2.0 - parameter);
integral := 0.0;
n := 0;
repeat
tan_2n_phi := tan(two_n * phi); // tan(90°) = -3.68934 E19 無限大になりません
sum := sum - two_n * (a - g) * (a - g);
two_n := two_n + two_n;
phi := phi - arctan((a - g) * tan_2n_phi / (a + g * tan_2n_phi * tan_2n_phi)) / two_n;
integral := integral + (a - g) * sin(two_n * phi);
g_old := g;
a_old := a;
a := (g_old + a_old) / 2;
g := sqrt(g_old * a_old);
inc(n);
until (abs(a_old - g_old) <= (a_old * LDBL_EPSILON));
F := phi / g;
Fk := PI / 2 / g;
E := 1 / 2 * integral + 1 / 4 * sum * phi / g;
Ek := PI / 8 / a * sum;
result := n;
end;
//--------------------------------------------------------------------------------------------------
// パラメータｍの値がマイナスの時のサブルーチン90°分割計算 実数計算。
function Elliptic_Integrals(phi, m: double; var F, Fk, E, Ek: double): integer;
var
n: integer;
pai, pis2: double;
begin
pai := PI;
pis2 := PI / 2;
n := trunc((phi + pis2) / pai);
phi := phi - n * pai;
n := n + n;
result := Landen_Transform(abs(phi), m, F, Fk, E, Ek);
if phi >= 0.0 then begin
F := F + n * Fk;
E := E + n * Ek;
end
else begin
F := n * Fk - F;
E := n * EK - E;
end;
end;
//--------------------------------------------------------------------------------------------------
// パラメータｍの値がｍ＜０の時の計算。
// パラメータの値をプラスに変換して計算します。
// 引数は複素数ですが虚数部がゼロなので実数計算します。
//--------------------------------------------------------------------------------------------------
function Elliptic_Integral_minus_m(phiin, min: variant; var Fin, Ein : variant): integer;
var
F, E: double;
K, EK : double;
dum : double;
signphi : double;
phi, m : double;
i : integer;
begin
phi := phiin.real;
m := min.real;
signphi := sign(phi);
phi := PI / 2 - abs(phi);
dum := sqrt(1.0 - m);
i := Elliptic_Integrals(phi, abs(m / (1.0 - m)), F, K, E, Ek);
F := signphi * (K - F) / dum;
E := signphi * (EK - E) * dum;
Fin.real := F;
Ein.real := E;
result := i;
end;
//--------------------------------------------------------------------------------------------------
// パラメータｍの値が 0 < ｍ <＝１の時の計算。
// 一般的な値の計算です。
// ｍ＝１の時はランデン変換積分計算はありません。
// 引数は複素数ですが、虚数部がゼロなので実数計算をします。
//--------------------------------------------------------------------------------------------------
function Elliptic_Integral_FS(phiin, min: variant; var Fin, Ein : variant): integer;
var
F, E: double;
n, i: integer;
K, Ek, m, phi: double;
begin
phi := phiin.real;
m := min.real;
if m = 1 then begin
if abs(phi) >= PI / 2 then begin
F := infinity;
if phi < 0 then F := -F;
end
else begin
K := tan(Phi);
F := sign(Phi) * ln(abs(K) + sqrt(1.0 + K * K));
end;
if (abs(phi) <= PI / 2) then begin
E := sin(phi);
end
else begin
n := trunc((abs(phi) + PI / 2) / PI);
E := n + n + sin(abs(phi) - n * PI);
if phi < 0 then E := - E;
end;
Fin.real := F;
Ein.real := E;
result := 0;
exit;
end;
// 90°分割計算
n := trunc((phi + PI / 2) / PI);
phi := phi - n * PI;
n := n + n;
i := Landen_Transform(abs(phi), m, F, K, E, Ek);
F := sign(phi) * F + n * K;
E := sign(phi) * E + n * Ek;
Fin.real := F;
Ein.real := E;
result := i;
end;
//--------------------------------------------------------------------------------------------------
//--------------------------------------------------------------------------------------------------
// 楕円の半径 あるいは 離心率から楕円積分計算をします。
// 離心率kの値として虚数入力可能文字の末尾にｉ付加です。
// kの値に入力制限はありません。
//--------------------------------------------------------------------------------------------------
procedure TForm1.BitBtn1Click(Sender: TObject);
var
ch, l : integer;
a, b, deg : double;
q, k, m, degb : double;
ac, bc : variant;
kc, mc, qc : variant;
F, E : variant;
kstr, kss : string;
c : char;
kssF : boolean;
degmax, kmax : double;
pai : double;
begin
val(radius_a_edit.Text, a, ch);
if ch <> 0 then begin
application.MessageBox('半径aの値に間違いがあります。','注意',0);
exit;
end;
if a <= 0 then begin
application.MessageBox('半径aの値は０より大きくして下さい。','注意',0);
exit;
end;
val(radius_b_edit.Text, b, ch);
if ch <> 0 then begin
application.MessageBox('半径bの値に間違いがあります。','注意',0);
exit;
end;
if b < 0 then begin
application.MessageBox('半径ｂの値は０以上にして下さい。','注意',0);
exit;
end;
val(arc_degree_edit.Text, deg, ch);
if ch <> 0 then begin
application.MessageBox('積分の範囲αの値に間違いがあります。','注意',0);
exit;
end;
if abs(deg) > 360 then begin
application.MessageBox('積分の範囲αの値は±360°以下にして下さい。','注意',0);
exit;
end;
kssF := false;
if checkbox1.Checked then begin // 離心率 k 指定なら
kstr := k_edit.Text;
if kstr = '' then begin
application.MessageBox('離心率kの値がありません。','注意',0);
exit;
end;
l := length(kstr); // 文字の長さ取得
c := kstr[l]; // iの文字確認
if (c = 'i') or (c = 'I') then begin // i虚数指定だったら
kssF := True; // 虚数フラグセット
kss := copy(kstr, 1, l - 1); // iの前までコピー
end
else Kss := kstr;
val(Kss, k, ch);
if ch <> 0 then begin
application.MessageBox('離心率kの値に間違いがあります。','注意',0);
exit;
end;
m := k * k;
if kssF then m := -m; // 虚数だったら m = -m
end
else begin // 離心率 k 指定でないなら k計算
m := 1 - b * b / a / a; // m = (a^2-b^2)/a^2 k = √m
k := sqrt(abs(m)); // kの絶対値 表示用
if m >= 0 then
k_edit.Text := floatTostr(k)
else
k_edit.Text := floatTostr(k) + 'i';
end;
memo1.Clear;
pai := pi; // pi extended => pai double
degb := deg; // 修正前の値を保存
q := deg / 180 * pai; // 角度rad変換
F := varcomplex(0, 0);
E := varcomplex(0 ,0);
ac := Varcomplex(a, 0); // 複素数に入力値セット
bc := Varcomplex(b, 0);
qc := Varcomplex(q, 0);
if checkbox1.Checked then // 離心率 k 指定なら
mc := Varcomplex(m, 0) // 入力値m=ki^2 セット
else
mc := (VarComplexSqr(ac) -VarComplexSqr(bc)) / VarComplexSqr(ac); // a,bの値からmの計算
kc := VarComplexSqrt(mc); // k = √m
if m > 1 then begin // k > 1 m > 1
ch := Large_Modulus_prus_complex(qc, kc, F, E); // k m が１より大きい場合の計算
degmax := arcsin(sqrt(1 / (k * k))) / pi * 180;
if abs(degb) < 90 then kmax := sin(abs(degb) / 180 * pi)
else kmax := 1;
if kmax <> 0 then begin
kmax := sqrt(1 / (kmax * kmax));
Form1.Memo1.Lines.Append('離心率固定の角度の最大値は ±' + floatTostr(degmax) + 'deg');
Form1.Memo1.Lines.Append('角度固定の離心率の最大値は ' + floatTostr(kmax));
end;
end
else begin
if m >= 0 then ch := Elliptic_Integral_FS(qc, mc, F, E); // ｍ＞＝０
if m < 0 then ch := Elliptic_Integral_minus_m(qc, mc, F, E); // ｍ＜ ０
end;
Memo1.Lines.Append(' Loop数 ＝ ' + inttostr(ch));
Memo1.Lines.Append(' 第１種 ' + floatTostr(F.real));
Memo1.Lines.Append(' ' + floatTostr(F.Imaginary) + 'i');
Memo1.Lines.Append(' 第２種 ' + floatTostr(E.real));
Memo1.Lines.Append(' ' + floatTostr(E.Imaginary) + 'i');
end;
// 判定値 LDBL_EPSILONの設定
procedure TForm1.FormCreate(Sender: TObject);
var
one, tmp: double;
begin
one := 1;
LDBL_EPSILON := one;
repeat
LDBL_EPSILON := LDBL_EPSILON / 2;
tmp := LDBL_EPSILON + one;
until tmp = one;
LDBL_EPSILON := LDBL_EPSILON * 2; // LDBL_EPSILON := 2^(1-32)
memo1.Clear;
memo1.Lines.Append('第１種、第２種楕円積分');
end;
end.
second_Elliptic_Landen_parameter.zip
各種プログラム計算例に戻る