2018-09-18 Qiita コミュニティ 2次曲線の式から楕円パラメータを導出する にあった:変換計算式の追加。
此処での変換式は、楕円の角度を求めるとき以外三角関数を使用せず、二元二次式の係数から全て求めています。
問題なく 長半径、短半径、角度、中心座標を求められます。
2017-08-16 新しい変換計算の確認
二元二次式から問題なく楕円の一般式 に変換できる計算方法があったので確認をしました。
以前の計算では、楕円の角度が45°の時、半径a, bの値が正確に求めることが出来ませんでした。
計算方法は、"楕円と楕円の衝突"その7 楕円と楕円の衝突に楕円の縦横変倍があるのですが、縦横変倍に二元二次式を利用していて、その中で二元二次式から一般式に変換を行っている計算があり、その計算で、どのような楕円の二元二次式の値でも正しく、長半径、短半径、角度、中心座標が求められことが分かりました。
これで、無駄な座標変換と、再計算は必要なくなります。
楕円の最小二乗法、ガウスジョルダン法による 二元二次方程式の係数推定値から、楕円一般式変換時の問題確認
楕円の二元二次方程式から、楕円の一般式に変換する計算の確認をしてみました。
楕円近似のプログラムに組み込まれていますが、楕円の角度45°の時の、半径a,bの値がズレ、座標変換をして半径を求める方法を追加したので、その時の検討内容です。
最小二乗法、ガウスジョルダンにより楕円の二元二次方程式を求めた時、楕円の一般式に変換しないと、楕円の描画が面倒になります。
楕円の一般式から、二元二次方程式に変換する場合は、計算は面倒ですが、確実に変換することが可能です。
但し、Sin関数、Cos関数等による桁落ちの問題はあります。
座標の値から、楕円の二元二次方程式の係数を求める場合、楕円の座標(X、Y)の点データーが最低5個あれば、AX^2+BXY+CY^2+DX+EY+Fの各係数の値を求めることが出来ます。
A~F迄の値をすべて求めるのは困難なので、Aの値を1に、或いはFの値を1に固定して、求めます。
二元二次方程式にしてしまうと、A~Fの値は、比率さえ変更しなければ、どんな値でもよく無限に存在するので、どれかを最初に固定して求める必要があります。
楕円の軸角 θ はArctan2(B, A-C) / 2 で、各値の比率が変わらなければ、簡単に求めることが出来ます。
又、中心座標も、Aの値が1になる様に係数を変更すれば、できます。
今までの計算方法では、半径aとbは、三角関数sinとcosを使用して、求めますが、軸角45°の時、sinとcosの値が同じになり、正しい値を求めることが出来ません。
しかし、新しい計算方法だと、問題なく正しい値を計算することができます。
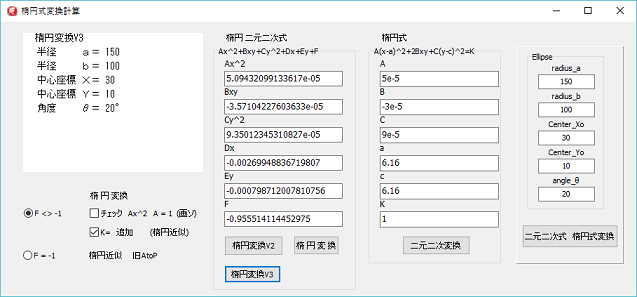
"楕円変換V2"のボタンが、楕円と楕円の衝突にあった計算方法の実行ボタンです。
"楕円変換V3"のボタンが、2次曲線の式から楕円パラメータを導出するによる計算の実行ボタンです。

楕円の半径a,b、中心座標Xo,Yo、角度θ を、二元二次方程式に変換し、各係数を求め、更に元の半径a,b、中心座標Xo,Yo、角度θ へ逆算するプログラムです。
上図左側は、二元二次に変換し、そのまま、逆変換した場合です。右側は、Aの値を1にした場合です。
楕円の角度が45°の場合、二元二次の係数の係数から、半径を計算しようとすると、上図右の様に半径a,bが同じ値になってしまいます。
プログラムは、イメージングソリューションにある逆変換の計算式を使用した場合です。
Fの値を1にして、逆変換する計算式も組み込んでみましたが、計算結果は同じように、半径a,bが同じ値になってしまいます。
色々なパターンについて、確認をすると、イメージングソリューションの逆変換計算は、45°ジャストの時に半径a,bが同じ値になり、僅かでもズレれば、かなり正解に近い値を得られるようです。
同じ様に、最小二乗法のプログラムで、楕円変換式のAtoPの計算も45°に近い角度の場合正しい半径の値を得ることが出来ません。
最小二乗法による計算の場合、元のデーターは、X,Yの座標データーであり、楕円の角度は正しい答えが得られることから、座標変換をして45°以外の角度にすれば、正しい半径の値を得ることが出来ます。
新しい その7 楕円と楕円の衝突
と
2次曲線の式から楕円パラメータを導出する の方法であれば、楕円の二元二次の値であれば、いつでも正しい結果が得られることがわかります。
次の計算例は、最小二乗法による楕円の係数を求めるプログラムで、45°の楕円の座標から二元二次の係数を求め、半径a,b、中心座標Xo,Yo、角度θ をイメージングソリューションの計算で求めている場合です。
ここのプログラムは、最小二乗法のプログラムで、楕円近似の古いプログラムです。
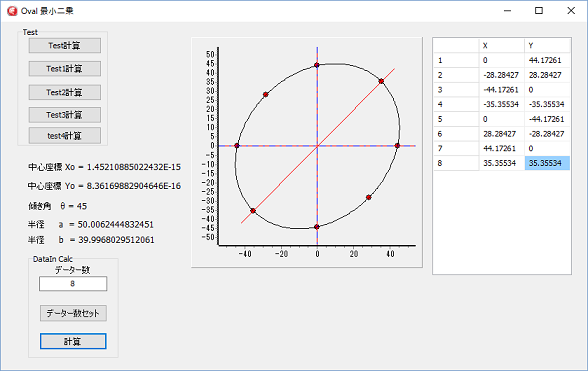
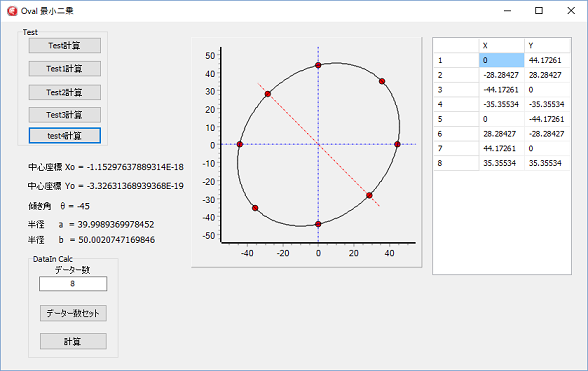
上図左は、演算精度Doubleで、右はEXtendedで計算しています。
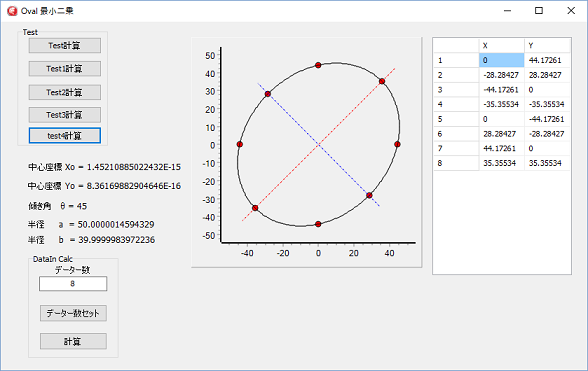
計算のデーターは、長半径が50で、短半径が40、中心座標0,0、軸角45°です。
不思議な事に、Doubleと、Extendedでは、半径a.bの値が逆になり、軸角+-逆になっています。
結果的には同じですが、やはり、Extendedの方が正解に近いです。
ジャスト45だと、半径a.bが同じになってしまう筈ですが、誤差が小さいので、45°表示されていますが、計算値はジャスト45°に成ってないようです。
試しにプログラムの中のArctan2(A, 1-B) / 2のBの値を if B=1 then **** とプログラムしてみると、1になっていないことが確認できます。
角度も、pi/4と比較すると、ジャスト45°ではないようです。
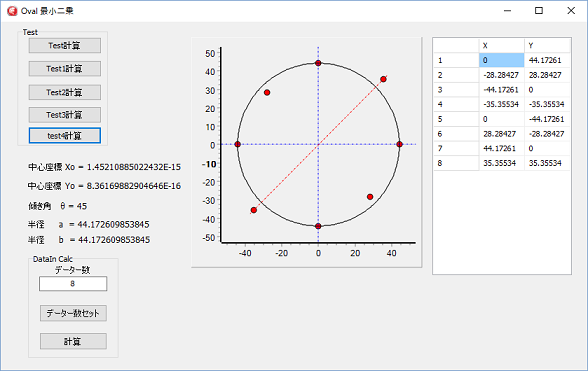
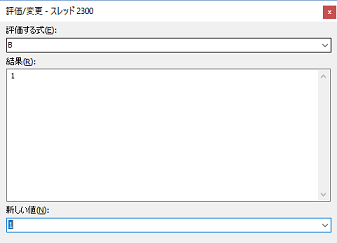
左図は、デバッグモードでArctan2(A, 1-B) / 2のBの値を1に強制変更した場合です。
上図は、デバッグ時の評価変更の画面で、評価時Bの値は1と表示されます。
しかし、新しい値に1といれ、新しい値に変更すると、左図の様に、半径a,bが同じ値になり円になります。
要するに、45°近辺の時、二進浮動小数点の値を、十進の値に変更して表示するとき、丸められて表示されない桁の値で計算されていることになります。
次は0°に座標変換して、半径a.bの値を求めたものです。
新しい計算方法であれば座標変換をしなくても正しい値を得ることができます。
 計算精度は、Doubleですが、半径は、かなり精度の高い結果となっています。
計算精度は、Doubleですが、半径は、かなり精度の高い結果となっています。
元のデーターが小数点以下5桁に対して、半径も小数点以下5桁の精度になっていてかなり良い結果となっています。
ガウスジョルダン法によるプログラム例
ガウスジョルダン法で、楕円の5点のデーターを入力して、楕円の値を求めるプログラムを検討してみました。
"新しい変換計算"にチェックを入れると、"座標変換"のチェックの有無に関わらず、座標変換計算は行われません。
新しい計算方法であればいつでも正しい結果が得られます。
変換確認プログラム
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.ExtCtrls, Vcl.StdCtrls, math;
type
TForm1 = class(TForm)
Image1: TImage;
Panel1: TPanel;
Ellipse1Box: TGroupBox;
radius_a1_Edit: TLabeledEdit;
radius_b1_Edit: TLabeledEdit;
Center_x1_Edit: TLabeledEdit;
Center_y1_Edit: TLabeledEdit;
angle_q1_Edit: TLabeledEdit;
Button2: TButton;
CheckBox1: TCheckBox;
RadioButton1: TRadioButton;
RadioButton2: TRadioButton;
GroupBox1: TGroupBox;
LabeledEdit7: TLabeledEdit;
LabeledEdit8: TLabeledEdit;
LabeledEdit9: TLabeledEdit;
LabeledEdit10: TLabeledEdit;
LabeledEdit11: TLabeledEdit;
Button4: TButton;
LabeledEdit12: TLabeledEdit;
Label1: TLabel;
CheckBox2: TCheckBox;
GroupBox2: TGroupBox;
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
LabeledEdit3: TLabeledEdit;
LabeledEdit4: TLabeledEdit;
LabeledEdit5: TLabeledEdit;
LabeledEdit6: TLabeledEdit;
Button1: TButton;
Button3: TButton;
Label2: TLabel;
Button5: TButton;
Label3: TLabel;
procedure Button1Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure Button2Click(Sender: TObject);
procedure Button3Click(Sender: TObject);
procedure Button4Click(Sender: TObject);
procedure Button5Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
function datainput(var A, B, C, D, E, F: double): boolean;
procedure elementsCalc; // 各要素計算
procedure elementCalc;
procedure quadratic_transform(a, b, x, y, qdeg: double; var A0, B0, C0, D0, E0, F0: double);
procedure imageClear;
procedure PtoA; // 係数変換 P to A
procedure AtoP; // 係数変換 A to P
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
var
A1, B1, C1, D1, E1, F1 : double;
LL : string;
Q : double; // 軸角
Xo, Yo : double; // 原点
Ar, Br : double;
// 画面の消去
procedure TForm1.imageClear;
begin
image1.Canvas.Brush.Style := bsSolid;
image1.Canvas.Brush.Color := clWhite;
image1.Canvas.FillRect(Rect(0, 0, image1.Width, image1.Height));
end;
//-------------------------------------
// AX^2 + BXY + CY^2 + DX + EY + F = 0
// 二元二次楕円式の値の入力処理
//-------------------------------------
function TForm1.datainput(var A, B, C, D, E, F: double): boolean;
var
ch : integer;
begin
result := false;
val(LabeledEdit1.Text, A, ch);
if ch <> 0 then begin
application.MessageBox('Aの入力に誤りがあります', '注意', 0);
exit;
end;
val(LabeledEdit2.Text, B, ch);
if ch <> 0 then begin
application.MessageBox('Bの入力に誤りがあります', '注意', 0);
exit;
end;
val(LabeledEdit3.Text, C, ch);
if ch <> 0 then begin
application.MessageBox('Cの入力に誤りがあります', '注意', 0);
exit;
end;
val(LabeledEdit4.Text, D, ch);
if ch <> 0 then begin
application.MessageBox('Dの入力に誤りがあります', '注意', 0);
exit;
end;
val(LabeledEdit5.Text, E, ch);
if ch <> 0 then begin
application.MessageBox('Eの入力に誤りがあります', '注意', 0);
exit;
end;
val(LabeledEdit6.Text, F, ch);
if ch <> 0 then begin
application.MessageBox('Fの入力に誤りがあります', '注意', 0);
exit;
end;
result := true;
end;
//-----------------------------------------------------------------------
// 此処での計算は、楕円の全ての二元二次式から 楕円の係数を計算できます
// AX^2 + BXY + CY^2 + DX + EY + F
// h,v 中心座標
// Q: 楕円の傾き角
// ar,br 楕円の半径
//-----------------------------------------------------------------------
procedure TForm1.Button3Click(Sender: TObject);
var
xy, cosQ, sinQ : double;
h, v : double;
At, Bt : double;
kd : double;
ar, br : double;
A, B, C, D, E, F : double;
begin
if not datainput(A, B, C, D, E, F) then exit;
// 楕円の各係数計算
xy := (B * B - 4 * A * C);
h := (2 * D * C - E * B) / xy; // 原点からのX方向移動量
v := (2 * A * E - D * B) / xy; // 原点からのy方向移動量
Q := - arctan2(B, C - A) / 2; // 標準楕円からの回転角
cosQ := cos(Q);
sinQ := sin(Q);
at := A * cosQ * cosQ + B * cosQ * sinQ + C * sinQ * sinQ;
bt := A * sinQ * sinQ - B * cosQ * sinQ + C * cosQ * cosQ;
kd := A * h * h + B * h * v + C * v * v + D * h + E * v + F;
imageClear;
image1.Canvas.TextOut(10, 0,' 楕円変換V2');
if (at * kd > 0) or (bt * kd > 0) then begin
image1.Canvas.TextOut(10, 120,' 半径が虚数なので双曲線です。');
ar := sqrt(abs(Kd / at)); // 虚数半径a
br := sqrt(abs(kd / bt)); // 虚数半径b
image1.Canvas.TextOut(20, 20, '半径 a= ' + floatTostrF(ar, ffGeneral, 8, 3) + 'i');
image1.Canvas.TextOut(20, 40, '半径 b= ' + floatTostrF(br, ffGeneral, 8, 3) + 'i');
end
else begin
ar := sqrt(-Kd / at); // 半径a
br := sqrt(-kd / bt); // 半径b
image1.Canvas.TextOut(20, 20, '半径 a= ' + floatTostrF(ar, ffGeneral, 8, 3));
image1.Canvas.TextOut(20, 40, '半径 b= ' + floatTostrF(br, ffGeneral, 8, 3));
end;
image1.Canvas.TextOut(20, 60, '中心座標 X= ' + floatTostrF(h, ffGeneral, 8, 3));
image1.Canvas.TextOut(20, 80, '中心座標 Y= ' + floatTostrF(v, ffGeneral, 8, 3));
image1.Canvas.TextOut(20, 100, '角度 θ= ' + floatTostrF(Q / pi * 180, ffGeneral, 10, 3)+'°');
end;
//--------------------------------------------------------------
// 楕円の二元二次から楕円係数変換
// AX^2 + 2BXY + CY^2 + 2DX + 2EY + F
// sinθ cosθを使用しない方法
// 参照 https://qiita.com/haniwo820/items/98670ea4abc545cf86b6
//--------------------------------------------------------------
procedure TForm1.Button5Click(Sender: TObject);
var
x0, y0: double;
ar, br, a2, b2 : double;
ab: double;
A, B, C, D, E, F : double;
begin
if not datainput(A, B, C, D, E, F) then exit;
B := B / 2;
D := D / 2;
E := E / 2;
x0 := 0;
y0 := 0;
a2 := 0;
b2 := 0;
if A * C - B * B <> 0 then begin
x0 := (B * E - C * D) / (A * C - B * B);
y0 := (B * D - A * E) / (A * C - B * B);
ab := 2 * ((C * D - B * E) * D + (A * E - B * D) * E - (A * C - B * B) * F);
if A + C - sqrt((A - C) * (A - C) + 4 * B * B) <> 0 then
a2 := ab / (A * C- B * B) / (A + C - sqrt((A - C) * (A - C) + 4 * B * B));
if A + C + sqrt((A - C) * (A - C) + 4 * B * B) <> 0 then
b2 := ab / (A * C- B * B) / (A + C + sqrt((A - C) * (A - C) + 4 * B * B));
end;
ar := sqrt(abs(a2));
br := sqrt(abs(b2));
Q := - arctan2((2 * B) , (C - A)) / 2;
imageClear;
image1.Canvas.TextOut(10, 0,' 楕円変換V3');
if (a2 < 0) or (b2 < 0) then begin
image1.Canvas.TextOut(10, 120,' 半径が虚数なので双曲線です。');
image1.Canvas.TextOut(20, 20, '半径 a= ' + floatTostrF(ar, ffGeneral, 8, 3) + 'i');
image1.Canvas.TextOut(20, 40, '半径 b= ' + floatTostrF(br, ffGeneral, 8, 3) + 'i');
end
else begin
image1.Canvas.TextOut(20, 20, '半径 a= ' + floatTostrF(ar, ffGeneral, 8, 3));
image1.Canvas.TextOut(20, 40, '半径 b= ' + floatTostrF(br, ffGeneral, 8, 3));
end;
image1.Canvas.TextOut(20, 60, '中心座標 X= ' + floatTostrF(x0, ffGeneral, 8, 3));
image1.Canvas.TextOut(20, 80, '中心座標 Y= ' + floatTostrF(y0, ffGeneral, 8, 3));
image1.Canvas.TextOut(20, 100, '角度 θ= ' + floatTostrF(Q / pi * 180, ffGeneral, 10, 3)+'°');
end;
//----------------------------------------------------
// A(x-a)^2 + 2Bxy + C(y-c) = K
// をAx^2 + Bxy + Cy^2 + Dx + Ey + F = 0 に変換します
//----------------------------------------------------
procedure TForm1.Button4Click(Sender: TObject);
var
ch : integer;
A, B, C, K : double;
sa, sc : double;
begin
val(LabeledEdit7.Text,A,ch);
if ch <> 0 then begin
application.MessageBox('Aは数値ではありません。', 'A', 0);
exit;
end;
val(LabeledEdit8.Text,B,ch);
if ch <> 0 then begin
application.MessageBox('Bは数値ではありません。', 'B', 0);
exit;
end;
val(LabeledEdit9.Text,C,ch);
if ch <> 0 then begin
application.MessageBox('Cは数値ではありません。', 'C', 0);
exit;
end;
val(LabeledEdit10.Text,sa,ch);
if ch <> 0 then begin
application.MessageBox('aは数値ではありません。', 'a', 0);
exit;
end;
val(LabeledEdit11.Text,sc,ch);
if ch <> 0 then begin
application.MessageBox('cは数値ではありません。', 'c', 0);
exit;
end;
val(LabeledEdit12.Text,K,ch);
if ch <> 0 then begin
application.MessageBox('Kは数値ではありません。', 'K', 0);
exit;
end;
LabeledEdit1.Text := floattostr(A);
LabeledEdit2.Text := floattostr(2 * B);
LabeledEdit3.Text := floattostr(C);
LabeledEdit4.Text := floattostr(-2 * A * sa);
LabeledEdit5.Text := floattostr(-2 * C * sc);
LabeledEdit6.Text := floattostr(A * sa * sa + C * sc * sc - K);
end;
//--------------------------------------------
// Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 から
// 通常の楕円データーに変換します
// Xo,Yo // 中心座標
// Q: // 楕円の傾き角
// Ao,Bo // 楕円の半径
//--------------------------------------------
procedure TForm1.Button1Click(Sender: TObject);
begin
// Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 の A,B,C,D,E,F の入力
if not datainput(A1, B1, C1, D1, E1, F1) then exit;
if RadioButton1.Checked then
if CheckBox1.Checked then elementCalc // 半径a, b 傾き角θ 中心座標Xo,yo 計算(画像ソリューション)
else elementsCalc; // 半径a, b 傾き角θ 中心座標Xo,yo 計算(最初の楕円近似計算)
if RadioButton2.Checked then AtoP; // 係数変換 A to P
end;
//--------------------------------------------------------
// 楕円の方程式 二元二次方程式への変換
// AX^2 + BXY + CY^2 + DX + EY + F の A,B,C,D,E,F
// 二元二次方程式から更に
// A(x-a)^2 + 2Bxy + C(y-c)^2 = 1 にへんかんします。
//--------------------------------------------------------
procedure TForm1.Button2Click(Sender: TObject);
var
Ch : integer;
a, c : double;
A0, B0, C0, K : double;
begin
// 楕円1のデーター
val(radius_a1_Edit.Text, ar, ch);
if ch <> 0 then begin
application.MessageBox('楕円の半径a数値ではありません。', '楕円の半径a', 0);
exit;
end;
if ar <= 0 then begin
application.MessageBox('楕円の半径aがゼロ 又はゼロ以下です。', '楕円の半径a', 0);
exit;
end;
val(radius_b1_Edit.Text, br, ch);
if ch <> 0 then begin
application.MessageBox('楕円の半径b数値ではありません。', '楕円の半径b', 0);
exit;
end;
if br <= 0 then begin
application.MessageBox('楕円の半径bがゼロ 又はゼロ以下です。', '楕円の半径b', 0);
exit;
end;
val(Center_x1_Edit.Text, Xo, ch);
if ch <> 0 then begin
application.MessageBox('楕円の中心位置x数値ではありません。', '楕円の中心位置x', 0);
exit;
end;
val(Center_y1_Edit.Text, Yo, ch);
if ch <> 0 then begin
application.MessageBox('楕円の中心位置y数値ではありません。', '楕円の中心位置y', 0);
exit;
end;
val(angle_q1_Edit.Text, q, ch);
if ch <> 0 then begin
application.MessageBox('楕円の角度θ数値ではありません。', '楕円の角度θ', 0);
exit;
end;
// 係数変換 Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0; (F = -1)
if RadioButton2.Checked then PtoA;
// 係数変換 Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0; (F <> -1)
if RadioButton1.Checked then quadratic_transform(ar, br, Xo, Yo, q, A1, B1, C1, D1, E1, F1);
LabeledEdit1.Text := floatTostr(A1);
LabeledEdit2.Text := floatTostr(B1);
LabeledEdit3.Text := floatTostr(C1);
LabeledEdit4.Text := floatTostr(D1);
LabeledEdit5.Text := floatTostr(E1);
LabeledEdit6.Text := floatTostr(F1);
// A(x-a)^2 + 2Bxy + C(y-c)^2 = 1 の式へ変換します
A0 := A1;
B0 := B1 / 2;
C0 := C1;
a := -D1 / 2 / A0;
c := -E1 / 2 / C0;
K := A0 * a * a + C0 * c * c - F1;
A0 := A0 / K;
B0 := B0 / K;
C0 := C0 / K;
K := 1;
LabeledEdit7.Text := floatTostr(A0);
LabeledEdit8.Text := floatTostr(B0);
LabeledEdit9.Text := floatTostr(C0);
LabeledEdit10.Text := floatTostr(a);
LabeledEdit11.Text := floatTostr(c);
LabeledEdit12.Text := floatTostr(K);
end;
//--------------- F使用ルーチンを追加した場合 使用可------------
// 楕円近似 最小二乗法ので最初に使用した計算方法
// 計算の中にFの値が有りませんでした
// 改良しFを使用したルーチン追加してみました。
// 角度θ, 中心座標 Xo, Y0 から K=Axo^2+Bxoyo+Cyo^2+Dxo+Eyo+Fで
// 計算されたKの値を使用しないと正しい答えが出ません
//---------------------------------------------------------------
procedure TForm1.elementsCalc; // 各要素計算
var
A, B, C, D, E : double;
K : double;
begin
A := A1 / 2;
B := B1 / 2;
C := C1 / 2;
D := D1 / 2;
E := E1 / 2;
if (A1 * C1 - B * B) = 0 then // 分母が0なのか確認する
begin
LL := '入力した値に誤りがあります。';
application.MessageBox(pointer(LL),'注意',0);
exit;
end;
Xo := (B * E - C1 * D) / (A1 * C1 - B * B);
Yo := (B * D - A1 * E) / (A1 * C1 - B * B);
Q := - arctan2(B1, C1 - A1); // 軸角の二倍
Ar := (A - C) * cos(Q) + B * sin(Q) + (A + C);
Br := (C - A) * cos(Q) - B * sin(Q) + (A + C);
imageClear;
if (Ar = 0) or (Br = 0) then begin
image1.Canvas.TextOut(10, 120,' 半径がゼロで楕円ではありません。');
exit;
end;
// Fの値を使用しない場合
if not CheckBox2.Checked then begin
image1.Canvas.TextOut(10, 0,' 楕円近似 K= 無し');
if (Ar < 0) or (Br < 0) then begin
image1.Canvas.TextOut(10, 120,' 半径が虚数なので双曲線です。');
Ar := abs(Ar);
Br := abs(Br);
end;
Ar := 1 / sqrt(Ar);
Br := 1 / sqrt(Br);
image1.Canvas.TextOut(20, 20, '半径 a= ' + floatTostrF(Ar, ffGeneral, 8, 3));
image1.Canvas.TextOut(20, 40, '半径 b= ' + floatTostrF(Br, ffGeneral, 8, 3));
end
// Fの値を使用した場合 K=Ax^2+Bxy+Cy^2+Dx+Ey+F 追加
else begin
image1.Canvas.TextOut(10, 0,' 楕円近似 K= 追加');
K := A1 * Xo * Xo + B1 * Xo * Yo + C1 * Yo * Yo + D1 * Xo + E1 * Yo + F1;
if (Ar * K > 0) or (Br * K > 0) then begin
image1.Canvas.TextOut(10, 120,' 半径が虚数なので双曲線です。');
Ar := sqrt(abs(K / Ar));
Br := sqrt(abs(K / Br));
image1.Canvas.TextOut(20, 20, '半径 a= ' + floatTostrF(Ar, ffGeneral, 8, 3) + 'i');
image1.Canvas.TextOut(20, 40, '半径 b= ' + floatTostrF(Br, ffGeneral, 8, 3) + 'i');
end
else begin
Ar := sqrt(-K / Ar);
Br := sqrt(-K / Br);
image1.Canvas.TextOut(20, 20, '半径 a= ' + floatTostrF(Ar, ffGeneral, 8, 3));
image1.Canvas.TextOut(20, 40, '半径 b= ' + floatTostrF(Br, ffGeneral, 8, 3));
end;
end;
Q := Q / 2; // 軸角
image1.Canvas.TextOut(20, 60, '中心座標 X= ' + floatTostrF(Xo, ffGeneral, 8, 3));
image1.Canvas.TextOut(20, 80, '中心座標 Y= ' + floatTostrF(Yo, ffGeneral, 8, 3));
image1.Canvas.TextOut(20, 100, '角度 θ= ' + floatTostrF(q / pi * 180, ffGeneral, 10, 3)+'°');
end;
//-------------------使用不可-----------------
// 楕円二元二次方程式を 楕円の通常式に変換
// 画像ソリューションにある計算方法
// 45°の時正しく半径を変換できません
//--------------------------------------------
procedure TForm1.elementCalc; // 各要素計算
var
A,B,C,D,E : double;
XPY2, EC2, XMY2, ES2, SWS: double;
begin
// Xo,Yo // 中心座標
// Q: // 楕円の傾き角
// Ao,Bo // 楕円の半径
// 行列inv_a と 行列bの積の結果から、直接c1[]を使用しても良いのだか
// 計算を分かりやすくするため、A~Eに値をコピーする
A := B1 / A1;
B := C1 / A1;
C := D1 / A1;
D := E1 / A1;
E := F1 / A1;
// 中心座標計算
if (4 * B - A * A) = 0 then // 分母が0なのか確認する
begin
LL := '入力した値に誤りがあります。';
application.MessageBox(pointer(LL),'注意',0);
exit;
end;
Xo := (A * D - 2 * B * C) / (4 * B - A * A);
Yo := (A * C - 2 * D) / (4 * B - A * A);
// 傾き角計算
Q := - arctan2(A ,(B - 1)) / 2;
// if B = 1 then Q := pi / 4
// else Q := arctan(A / (1 - B)) / 2;
// Q := arctan(A / (1 - B)) / 2 - pi / 2; // 角度を90どずらすと、半径 A と B が逆になる
// 半径 A 計算
XPY2 := (Xo * cos(Q) + Yo * sin(Q)) * (Xo * cos(Q) + Yo * sin(Q));
EC2 := E * cos(Q) * cos(Q);
XMY2 := (Xo * sin(Q) - Yo * cos(Q)) * (Xo * sin(Q) - Yo * cos(Q));
ES2 := E * sin(Q) * sin(Q);
SWS := (sin(Q) * sin(Q) - B * cos(Q) * cos(Q)) / (cos(Q) * cos(Q) - B * sin(Q) * sin(Q));
Ar := sqrt(abs(XPY2 - EC2 - (XMY2 - ES2) * SWS));
// 半径 B 計算
XPY2 := (Xo * sin(Q) - Yo * cos(Q)) * (Xo * sin(Q) - Yo * cos(Q));
EC2 := E * sin(Q) * sin(Q);
XMY2 := (Xo * cos(Q) + Yo * sin(Q)) * (Xo * cos(Q) + Yo * sin(Q));
ES2 := E * cos(Q) * cos(Q);
SWS := (cos(Q) * cos(Q) - B * sin(Q) * sin(Q)) / (sin(Q) * sin(Q) - B * cos(Q) * cos(Q));
Br := sqrt(abs(XPY2 - EC2 - (XMY2 - ES2) * SWS));
imageClear;
image1.Canvas.TextOut(10, 0,' 画像処理 ソリューション');
image1.Canvas.TextOut(20, 20, '半径 a= ' + floatTostrF(Ar, ffGeneral, 8, 3));
image1.Canvas.TextOut(20, 40, '半径 b= ' + floatTostrF(Br, ffGeneral, 8, 3));
image1.Canvas.TextOut(20, 60, '中心座標 X= ' + floatTostrF(Xo, ffGeneral, 8, 3));
image1.Canvas.TextOut(20, 80, '中心座標 Y= ' + floatTostrF(Yo, ffGeneral, 8, 3));
image1.Canvas.TextOut(20, 100, '角度 θ= ' + floatTostrF(q / pi * 180, ffGeneral, 10, 3)+'°');
end;
//-------------------------------------------------
// 楕円の方程式 二次方程式への変換
// AX^2 + BXY + CY^2 + DX + EY + F の A,B,C,D,E,F
// F <> -1 と A = 1
//-------------------------------------------------
procedure TForm1.quadratic_transform(a, b, x, y, qdeg: double; var A0, B0, C0, D0, E0, F0: double);
var
Q : double;
sin_Q, cos_q : double;
ah2, bh2 : double;
sinh2, cosh2 : double;
sincosQ : double;
xh2, yh2, xy : double;
begin
Q := qdeg / 180 * pi; // ラジアン単位に変換
sin_Q := sin(Q);
cos_Q := cos(Q);
ah2 := a * a;
bh2 := b * b;
sinh2 := sin_Q * sin_Q;
cosh2 := cos_Q * cos_Q;
sincosQ := sin_Q * cos_Q;
xh2 := x * x;
yh2 := y * y;
xy := x * y;
A0 := cosh2 / ah2 + sinh2 / bh2;
B0 := 2 * (1 / ah2 - 1 / bh2) * sincosQ;
C0 := sinh2 / ah2 + cosh2 / bh2;
D0 := -2 * ((x * cosh2 + y * sincosQ) / ah2 + (x * sinh2 - y * sincosQ) / bh2);
E0 := -2 * ((x * sincosQ + y * sinh2) / ah2 + (y * cosh2 - x * sincosQ) / bh2);
F0 := (xh2 * cosh2 + 2 * xy * sincosQ + yh2 * sinh2) / ah2
+ (xh2 * sinh2 - 2 * xy * sincosQ + yh2 * cosh2) / bh2
- 1;
// A = 1 に変換します
if CheckBox1.Checked then begin
B0 := B0 / A0;
C0 := C0 / A0;
D0 := D0 / A0;
E0 := E0 / A0;
F0 := F0 / A0;
A0 := A0 / A0;
end;
end;
//-----------------------------------------------------------
// 楕円の方程式 Ax^2 + Bxy + Cy^2 + Dx + Ey + F に変換
// F = -1 に変換
// ○/F が無ければ通常の変換ですがその時はFの符号を反転します
//-----------------------------------------------------------
procedure TForm1.PtoA; // 係数変換 P to A
var
C, S, F: double;
begin
Q := q / 180 * pi;
C := COS(Q);
S := SIN(Q);
F := 1 - Power(((Xo * C + Yo * S) / ar), 2) - Power(((Xo * S - Yo * C) / br), 2);
// F1 := Power(((Xo * C + Yo * S) / ar), 2) + Power(((Xo * S - Yo * C) / br), 2) - 1;
A1 := Power((C / ar), 2) + Power((S / br), 2);
B1 := (1 / Power(ar, 2) - 1 / Power(br, 2)) * C * S * 2;
C1 := Power(S / ar, 2) + Power(C / br, 2);
D1 := - (Xo * C + Yo * S) * C * 2 / Power(ar, 2) - (Xo * S - Yo * C) * S * 2 / Power(br, 2);
E1 := - (Xo * C + Yo * S) * S * 2 / Power(ar, 2) + (Xo * S - Yo * C) * C * 2 / Power(br, 2);
// F1 を使用した場合以下不要です
A1 := A1 / F;
B1 := B1 / F;
C1 := C1 / F;
D1 := D1 / F;
E1 := E1 / F;
F1 := -1;
end;
//-------------------使用不可-----------------------------------
// 楕円近似計算最小二乗法+ガウスニュートン法で使用していた計算
// Ax^2 + Bxy + Cy^2 + Dx + Ey + F から
// 半径 a, b 角度θ 座標 Xo, Yo に変換します
// F = -1 でないと正しく変換できません
// 楕円の角度が45度の時は半径a, b を正しく計算できません
// a,bの値が同じになってしまいます。
//--------------------------------------------------------------
procedure TForm1.AtoP; // 係数変換 A to P
var
C, S, K: double;
begin
Q := - 1 / 2 * ARCTAN2(B1, (C1 - A1));
C := COS(Q);
S := SIN(Q);
// 下記に変更すれば F1 = -1 でなくてもOKです
// K := 1 / (-F1 + (C * C - S * S) / 4
K := 1 / (1 + (C * C - S * S) / 4
* (Power((D1 * C + E1 * S), 2) / (A1 * C * C - C1 * S * S)
- Power((D1 * S - E1 * C), 2) / (A1 * S * S - C1 * C * C)));
// 次の計算ar,brは45°の時あきらかに同じ値になります
ar := Sqrt(Abs( (C * C - S * S) / (A1 * C * C - C1 * S * S) / K));
br := Sqrt(Abs(-(C * C - S * S) / (A1 * S * S - C1 * C * C) / K));
Xo :=-(ar * ar * C * (D1 * C + E1 * S) + br * br * S * (D1 * S - E1 * C)) / 2 * K;
Yo :=-(ar * ar * S * (D1 * C + E1 * S) - br * br * C * (D1 * S - E1 * C)) / 2 * K;
imageClear;
image1.Canvas.TextOut(10, 0,' 楕円近似 AtoP');
image1.Canvas.TextOut(20, 20, '半径 a= ' + floatTostrF(Ar, ffGeneral, 8, 3));
image1.Canvas.TextOut(20, 40, '半径 b= ' + floatTostrF(Br, ffGeneral, 8, 3));
image1.Canvas.TextOut(20, 60, '中心座標 X= ' + floatTostrF(Xo, ffGeneral, 8, 3));
image1.Canvas.TextOut(20, 80, '中心座標 Y= ' + floatTostrF(Yo, ffGeneral, 8, 3));
image1.Canvas.TextOut(20, 100, '角度 θ= ' + floatTostrF(q / pi * 180, ffGeneral, 10, 3)+'°');
end;
//-----------------------
// 初期設定
//-----------------------
procedure TForm1.FormCreate(Sender: TObject);
begin
imageClear;
image1.Canvas.Font.Name := 'MS ゴシック';
// image1.Canvas.Font.Style := [fsbold];
image1.Canvas.Font.Height := 14;
end;
end.
ガウスジョルダン法のプログラム例
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, VclTee.TeeGDIPlus, Vcl.StdCtrls, Vcl.ExtCtrls,
VCLTee.TeEngine, VCLTee.Series, VCLTee.TeeProcs, VCLTee.Chart, Vcl.Grids, math;
type
TForm1 = class(TForm)
StringGrid1: TStringGrid;
Chart1: TChart;
Series1: TPointSeries;
Button1: TButton;
GroupBox2: TGroupBox;
LabeledEdit1: TLabeledEdit;
Button3: TButton;
Button4: TButton;
Image1: TImage;
Button2: TButton;
CheckBox1: TCheckBox;
CheckBox2: TCheckBox;
procedure Button1Click(Sender: TObject);
procedure Button3Click(Sender: TObject);
procedure Button4Click(Sender: TObject);
procedure Chart1AfterDraw(Sender: TObject);
procedure Button2Click(Sender: TObject);
private
{ Private 宣言 }
procedure StrinGridset; // データー表示
procedure calcDsp; // 計算表示
procedure imageClear;
procedure sigmaCalc; // Σの計算
procedure DotGraph; // データーグラフ表示
procedure XYMAXScaleSet; // スケールセット 縦横比を同じにするため
procedure OvalGraph; // 楕円描画
procedure testdataset; // テストデーターの読み込み
procedure test1dataset; // テストデーターの読み込み
procedure coordinate_converter; // 座標変換
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
type
TGaussA = array of array of double;
TGaussB = array of double;
const
unknowns = 5;
var
// 入力データーの数
nd : integer;
// 入力データー
data: array of array of double;
// 座標変換用
Cdata: array of array of double;
Ga: TGaussA; Gb: TGaussB;
A, B, C, D, E, F: double;
ar, br, Xo, Yo, Q : double;
maxn : integer;
// テスト用楕円データー
Testdata: array[0..4,0..1] of string = (('-125.127','134.797'),
('-129.240',' 66.143'),
(' -75.660',' 35.356'),
(' -50.398','110.839'),
(' -95.329','141.0157'));
Testdata1: array[0..4,0..1] of string = ((' 50.00000',' 50.00000'),
('-40.00000',' 40.00000'),
('-50.00000','-50.00000'),
(' 40.00000','-40.00000'),
(' 62.4695047554424262',' 0.00000'));
procedure TForm1.imageClear;
begin
image1.Canvas.Brush.Style := bsSolid;
image1.Canvas.Brush.Color := clWhite;
image1.Canvas.FillRect(Rect(0, 0, image1.Width, image1.Height));
end;
procedure TForm1.OvalGraph; // 楕円描画
var
JJ: integer;
// KK: integer;
Xpos,Ypos: integer;
// AoXo,BoYo,MAoXo,MBoYo: integer;
W: double; // 角度ω
leftD,rightD,topD,BottomD: integer;
begin
Chart1.Canvas.Pen.Color := clBlack;
Chart1.Canvas.Pen.Width := 1;
Chart1.Canvas.Pen.Style := PsSolid;
Chart1.Canvas.Brush.Style := Bsclear;
// 角度を1度毎に分解し計算楕円作図 推定値 楕円半径 A,B 中心位置 X0, Y0 傾き角 θ を使用します
W := 0;
Xpos := Series1.CalcXPosValue(Ar * cos(W) * cos(Q) - Br * sin(W) * sin(Q) + Xo); // X座標 Ao * cos(W) * cos(Q) - Bo * sin(W) * sin(Q) + Xo
Ypos := Series1.CalcYPosValue(Ar * cos(W) * sin(Q) + Br * sin(W) * cos(Q) + Yo); // Y座標 Ao * cos(W) * sin(Q) + Bo * sin(W) * cos(Q) + Yo
Chart1.Canvas.MoveTo(Xpos,Ypos); // Series1.CalcXPosValue(X座標) Chart 上のX位置を求める
for JJ := 0 to 360 do // Series1.CalcYPosValue(Y座標) Chart 上のY位置を求める
begin
W := 2 * pi / 360 * JJ;
Xpos := Series1.CalcXPosValue(Ar * cos(W) * cos(Q) - Br * sin(W) * sin(Q) + Xo);
Ypos := Series1.CalcYPosValue(Ar * cos(W) * sin(Q) + Br * sin(W) * cos(Q) + Yo);
Chart1.Canvas.LineTo(Xpos,Ypos);
end;
// 中心線描画
leftD := Chart1.ChartRect.Left;
rightD := Chart1.ChartRect.Right;
topD := Chart1.ChartRect.Top;
BottomD := Chart1.ChartRect.Bottom;
Xpos := Series1.CalcXPosValue(Xo);
Ypos := Series1.CalcYPosValue(Yo);
Chart1.Canvas.Pen.Color := clBlue;
Chart1.Canvas.Pen.Width := 1;
Chart1.Canvas.Pen.Style := PsDashdot;
Chart1.Canvas.MoveTo(Xpos, topD);
Chart1.Canvas.LineTo(Xpos, BottomD);
Chart1.Canvas.MoveTo(leftD, Ypos);
Chart1.Canvas.LineTo(rightD, Ypos);
// 傾き線の描画
Chart1.Canvas.Pen.Color := clRed;
Xpos := Series1.CalcXPosValue(Ar * 1.2 * cos(Q) + Xo);
Ypos := Series1.CalcYPosValue(Ar * 1.2 * sin(Q) + Yo);
Chart1.Canvas.MoveTo(Xpos,Ypos);
Xpos := Series1.CalcXPosValue(-Ar * 1.2 * cos(Q) + Xo);
Ypos := Series1.CalcYPosValue(-Ar * 1.2 * sin(Q) + Yo);
Chart1.Canvas.LineTo(Xpos,Ypos);
end;
procedure TForm1.testdataset; // テストデーターの読み込み
var
JJ,II: integer;
begin
setlength(data , nd, 2); // データー数分の配列確保
for JJ := 0 to nd - 1 do
begin
for II := 0 to 1 do
data[JJ, II] := strTofloat(Testdata[JJ, II]); // テストデーター
end;
StrinGridset;
for II := 0 to nd - 1 do
begin
stringGrid1.Cells[1, II + 1] := Testdata[II, 0];
stringGrid1.Cells[2, II + 1] := Testdata[II, 1];
end;
end;
procedure TForm1.test1dataset; // テストデーターの読み込み
var
JJ,II: integer;
begin
setlength(data , nd, 2); // データー数分の配列確保
for JJ := 0 to nd - 1 do
begin
for II := 0 to 1 do
data[JJ, II] := strTofloat(Testdata1[JJ, II]); // テストデーター
end;
StrinGridset;
for II := 0 to nd - 1 do
begin
stringGrid1.Cells[1, II + 1] := Testdata1[II, 0];
stringGrid1.Cells[2, II + 1] := Testdata1[II, 1];
end;
end;
procedure TForm1.XYMAXScaleSet; // スケールセット 縦横比を同じにするため
var // のAxis設定
XBMin,XBMax,YLMin,YLMax: double;
BRange, LRange, W : double;
Xposd, Yposd: double;
JJ: integer;
SCsetF : Boolean;
begin
XBMax := data[0, 0];
XBMin := data[0, 0];
YLMax := data[0, 1];
YLMin := data[0, 1];
for JJ := 1 to nd -1 do
begin
if XBMax < data[JJ, 0] then // Xの最大値検索
XBMax := data[JJ, 0]; // Xの最大値
if XBMin > data[JJ, 0] then // Xの最小値検索
XBMin := data[JJ, 0]; // Xの最小値
if YLMax < data[JJ, 1] then // Yの最大値検索
YLMax := data[JJ, 1]; // Yの最大値
if YLMin > data[JJ, 1] then // Yの最小値検索
YLMin := data[JJ, 1]; // Yの最小値
end;
for JJ := 0 to 360 do // Series1.CalcYPosValue(Y座標) Chart 上のY位置を求める
begin
W := 2 * pi / 360 * JJ;
Xposd := Ar * cos(W) * cos(Q) - Br * sin(W) * sin(Q) + Xo;
Yposd := Ar * cos(W) * sin(Q) + Br * sin(W) * cos(Q) + Yo;
if XBMax < Xposd then // Xの最大値検索
XBMax := Xposd; // Xの最大値
if XBMin > Xposd then // Xの最小値検索
XBMin := Xposd; // Xの最小値
if YLMax < Yposd then // Yの最大値検索
YLMax := Yposd; // Yの最大値
if YLMin > Yposd then // Yの最小値検索
YLMin := Yposd; // Yの最小値
end;
BRange := XBMax - XBMin;
LRange := YLMax - YLMin;
if BRange > LRange then LRange := BRange;
if LRange = 0 then LRange := 1; // グラフのレンジが0になるのを防止する
XBMin := Xo - LRange * 0.6;
XBMax := Xo + LRange * 0.6;
YLMin := Yo - LRange * 0.6;
YLMax := Yo + LRange * 0.6;
Chart1.LeftAxis.Automatic := False;
Chart1.BottomAxis.Automatic := False;
SCsetF := False;
if Chart1.LeftAxis.Maximum < YLMin then
begin
Chart1.LeftAxis.Maximum := YLMax;
Chart1.LeftAxis.Minimum := YLMin;
SCsetF := True;
end;
if Chart1.LeftAxis.Minimum > YLMax then
begin
Chart1.LeftAxis.Minimum := YLMIN;
Chart1.LeftAxis.Maximum := YLMAX;
SCsetF := True;
end;
if not SCsetF then
begin
Chart1.LeftAxis.Maximum := YLMax;
Chart1.LeftAxis.Minimum := YLMin;
end;
SCsetF := False;
if Chart1.BottomAxis.Maximum < XBMin then
begin
Chart1.BottomAxis.Maximum := XBMax;
Chart1.BottomAxis.Minimum := XBMin;
SCsetF := True;
end;
if Chart1.BottomAxis.Minimum > XBMax then
begin
Chart1.BottomAxis.Minimum := XBMin;
Chart1.BottomAxis.Maximum := XBMax;
SCsetF := True;
end;
if not SCsetF then
begin
Chart1.BottomAxis.Maximum := XBMax;
Chart1.BottomAxis.Minimum := XBMin;
end;
end;
procedure TForm1.DotGraph; // データーグラフ表示
var
JJ : integer;
begin
Series1.Clear; // グラフクリア
XYMAXScaleSet; // スケールセット
for JJ := 0 to nd -1 do
Series1.AddXY(data[JJ, 0], data[JJ, 1], '', clRed);
// Series1.AddXY(data[JJ, 0], data[JJ, 1], intTostr(JJ), clRed);
// Series1.Marks.Visible:=True;
end;
procedure TForm1.StrinGridset; // データー表示
var
I: integer;
begin
stringGrid1.DefaultRowHeight := 20;
if nd < 1 then stringGrid1.RowCount := 2 // 固定行が1行あるので少なくても2行にする
else stringGrid1.RowCount := nd + 1; // 固定行を1行追加する
stringGrid1.ColCount := 3; // No, X, Y で3列
stringGrid1.ClientHeight := (stringGrid1.DefaultRowHeight + 1) * 16;
stringGrid1.ClientWidth := (stringGrid1.DefaultColWidth + 1) * 3;
stringGrid1.Cells[1, 0] := 'X';
stringGrid1.Cells[2, 0] := 'Y';
if nd = 0 then exit;
for I := 0 to nd - 1 do
begin
stringGrid1.Cells[0, I + 1] := intTostr(I + 1);
// stringGrid1.Cells[1, I + 1] := '';
// stringGrid1.Cells[2, I + 1] := '';
end;
end;
//-----------------------------------------------------------------------------------------
// 連立方程式の解法 ガウス-ジョルダン法
// n:n次方程式
// a:係数を表すn次元配列 入力データー
// b:非同次項を表す1次配列 解
//
// http://www.yamamo10.jp/yamamoto/lecture/2006/5E/Linear_eauations/gaussj_html/node2.html
//-----------------------------------------------------------------------------------------
function gauss_jordan(n: integer; var a: TGaussA; var b: TGaussB): boolean;
var
ipv, i, j : integer;
inv_pivot, temp : real;
big : real;
pivot_row : integer;
// row : array of integer;
begin
result := True;
// setlength(row, unknowns);
pivot_row := -1;
for ipv := 0 to n - 1 do begin
//最大値検索
big := 0.0;
for i := ipv to n - 1 do begin
if abs(a[i, ipv]) > big then begin
big := abs(a[i, ipv]);
pivot_row := i;
end;
end;
if big = 0 then begin
Result := False;
Exit;
end;
// row[ipv] := pivot_row;
// 行の入れ替え
if (ipv <> pivot_row) then begin
for i := 0 to n - 1 do begin
temp := a[ipv, i];
a[ipv, i] := a[pivot_row, i];
a[pivot_row, i] := temp;
end;
temp := b[ipv];
b[ipv] := b[pivot_row];
b[pivot_row] := temp;
end;
// 対角成分=1 ピボット行の処理
inv_pivot := 1.0 / a[ipv, ipv];
a[ipv,ipv] := 1.0;
for j := 0 to n - 1 do begin
a[ipv, j] := a[ipv, j] * inv_pivot;
end;
b[ipv] := b[ipv] * inv_pivot;
// ピボット列=0 ピボット行以外ノ処理
for i := 0 to n - 1 do begin
if (i <> ipv) then begin
temp := a[i, ipv];
a[i, ipv] := 0.0;
for j := 0 to n - 1 do begin
a[i, j] := a[i,j] - temp * a[ipv, j];
end;
b[i] := b[i] - temp * b[ipv];
end;
end;
end;
// 列の入れ替え 逆行列
// 逆行列は使用されません
{ for j := n - 1 downto 0 do begin
if (j <> row[j]) then begin
for i := 0 to n - 1do begin
temp := a[i, j];
a[i, j] := a[i, row[j]];
a[i, row[j]] := temp;
end;
end;
end; }
end;
// 楕円の傾き角で座標変換をします
// 座標変換前の中心座標を計算しておきます
// 座標変換後ガウスジョルダン法で連立方程式を解きます
procedure TForm1.coordinate_converter; // 座標変換
var
lng, QQ : double;
i, j : integer;
Xi, Yi : double;
begin
setlength(Cdata , nd, 2); // データー数分の配列確保
// 座標変換
for j := 0 to nd - 1 do begin
lng := sqrt(data[j, 1] * data[j, 1] + data[j, 0] * data[j, 0]);
QQ := arctan2(data[j, 1], data[j, 0]);
QQ := QQ - Q;
Cdata[j, 0] := lng * cos(QQ);
Cdata[j, 1] := lng * sin(QQ);
end;
// ガウスデータークリア
for i := 0 to maxn - 1 do begin
Gb[i] := 0;
for j := 0 to maxn -1 do
Ga[i, j] := 0;
end;
for i := 0 to nd - 1 do begin // x^2 xy y^2 x y の値セット 5 x 5
Ga[i, 0] := Cdata[i, 0] * Cdata[i, 0];
Ga[i, 1] := Cdata[i, 0] * Cdata[i, 1];
Ga[i, 2] := Cdata[i, 1] * Cdata[i, 1];
Ga[i, 3] := Cdata[i, 0];
Ga[i, 4] := Cdata[i, 1];
Gb[i] := 1;
end;
// 連立方程式をガウス-ジョルダン法で解く
// 此処で計算された、半径が採用されます
if gauss_jordan(unknowns, Ga, Gb) then begin
A := Gb[1] / Gb[0];
B := Gb[2] / Gb[0];
C := Gb[3] / Gb[0];
D := Gb[4] / Gb[0];
E := -1 / Gb[0];
// 中心の座標
Xi := (A * D - 2 * B * C) / (4 * B - A * A);
Yi := (A * C - 2 * D) / (4 * B - A * A);
// 傾き
QQ := ArcTan2(A ,(1 - B)) / 2.0;
// X軸方向の長さA
ar := sqrt(abs(sqr(Xi * cos(QQ) + Yi * sin(QQ)) - E * sqr(cos(QQ)) -
(sqr(Xi * sin(QQ) - Yi * cos(QQ)) - E * sqr(sin(QQ))) *
(sqr(sin(QQ)) - B * sqr(cos(QQ))) / (sqr(cos(QQ))- B * sqr(sin(QQ)))));
// Y軸方向の長さB
br := sqrt(abs(sqr(Xi * sin(QQ) - Yi * cos(QQ)) - E * sqr(sin(QQ)) -
(sqr(Xi * cos(QQ) + Yi * sin(QQ)) - E * sqr(cos(QQ))) *
(sqr(cos(QQ)) - B * sqr(sin(QQ))) / (sqr(sin(QQ)) - B * sqr(cos(QQ)))));
end
else
application.MessageBox('方程式の解法が出来ませんでした。','注意',0)
end;
// 方程式の解法と表示
// ガウスジョルダン法で方程式を解きます
// 座標変換の指定がある場合は、座標変換ガウスジョルダンのルーチンを呼び出します
procedure TForm1.sigmaCalc;
var
i, j : integer;
sinQ, cosQ: double;
xy, h, v, at, bt, kd: double;
begin
maxn := unknowns;
setlength(Ga, maxn, maxn);
setlength(Gb, maxn);
for i := 0 to maxn - 1 do begin
Gb[i] := 0;
for j := 0 to maxn -1 do
Ga[i, j] := 0;
end;
for i := 0 to nd - 1 do begin // x^2 xy y^2 x y の値セット 5 x 5
Ga[i, 0] := data[i, 0] * data[i, 0];
Ga[i, 1] := data[i, 0] * data[i, 1];
Ga[i, 2] := data[i, 1] * data[i, 1];
Ga[i, 3] := data[i, 0];
Ga[i, 4] := data[i, 1];
Gb[i] := 1; // Eの値を-1にします
end;
// 連立方程式をガウス-ジョルダン法で解く
// 座標変換をする場合は、中心座標と、軸角が採用されます
// 軸角が45°であると、半径が正しく計算されないので座標変換をして
// 半径を計算します。
// 角度は、短辺側の角度が計算されます。
if gauss_jordan(unknowns, Ga, Gb) then begin
if checkbox2.Checked = true then begin
A := Gb[0];
B := Gb[1];
C := Gb[2];
D := Gb[3];
E := Gb[4];
F := -1;
// 楕円の各係数計算
xy := (B * B - 4 * A * C);
h := (2 * D * C - E * B) / xy; // 原点からのX方向移動量
v := (2 * A * E - D * B) / xy; // 原点からのy方向移動量
Q := - arctan2(B, C - A) / 2; // 標準楕円からの回転角
if Q < 0 then Q := Q + pi;
cosQ := cos(Q);
sinQ := sin(Q);
at := A * cosQ * cosQ + B * cosQ * sinQ + C * sinQ * sinQ;
bt := A * sinQ * sinQ - B * cosQ * sinQ + C * cosQ * cosQ;
kd := A * h * h + B * h * v + C * v * v + D * h + E * v + F;
ar := sqrt(-Kd / at); // 半径a
br := sqrt(-kd / bt); // 半径b
xo := h;
yo := v;
end
else begin
A := Gb[1] / Gb[0];
B := Gb[2] / Gb[0];
C := Gb[3] / Gb[0];
D := Gb[4] / Gb[0];
E := -1 / Gb[0];
// 中心の座標
Xo := (A * D - 2 * B * C) / (4 * B - A * A);
Yo := (A * C - 2 * D) / (4 * B - A * A);
// 傾き
Q := ArcTan2(A ,(1 - B)) / 2.0;
if checkbox1.Checked = true then coordinate_converter // 座標変換
else begin
sinQ := sin(Q);
cosQ := cos(Q);
// X軸方向の長さA
ar := sqrt(abs(sqr(Xo * cosQ + Yo * sinQ) - E * sqr(cosQ) -
(sqr(Xo * sinQ - Yo * cosQ) - E * sqr(sinQ)) *
(sqr(sinQ) - B * sqr(cosQ)) / (sqr(cosQ)- B * sqr(sinQ))));
// Y軸方向の長さB
br := sqrt(abs(sqr(Xo * sinQ - Yo * cos(Q)) - E * sqr(sinQ) -
(sqr(Xo * cosQ + Yo * sinQ) - E * sqr(cosQ)) *
(sqr(cosQ) - B * sqr(sinQ)) / (sqr(sinQ) - B * sqr(cosQ))));
end;
end;
imageClear;
image1.Canvas.TextOut(20, 20, '半径 a= ' + floatTostrF(Ar, ffGeneral, 8, 3));
image1.Canvas.TextOut(20, 40, '半径 b= ' + floatTostrF(Br, ffGeneral, 8, 3));
image1.Canvas.TextOut(20, 60, '中心座標 X= ' + floatTostrF(Xo, ffGeneral, 8, 3));
image1.Canvas.TextOut(20, 80, '中心座標 Y= ' + floatTostrF(Yo, ffGeneral, 8, 3));
image1.Canvas.TextOut(20, 100, '角度 θ= ' + floatTostr(Q / pi * 180) + '°');
end
else
application.MessageBox('方程式の解法が出来ませんでした。','注意',0)
end;
procedure TForm1.calcDsp; // 計算表示
begin
sigmaCalc; // Σの計算
DotGraph; // データーグラフ表示
end;
procedure TForm1.Chart1AfterDraw(Sender: TObject);
begin
if nd = 0 then exit; // nd が 0 だったら 楕円描画しない
OvalGraph; // 楕円描画
end;
procedure TForm1.Button1Click(Sender: TObject);
begin
nd := unknowns; // テストデーター数
LabeledEdit1.Text := intTostr(nd);
testdataset; // テストデーターの読み込み
calcDsp; // 計算表示
end;
procedure TForm1.Button2Click(Sender: TObject);
begin
nd := unknowns; // テストデーター数
LabeledEdit1.Text := intTostr(nd);
test1dataset; // テストデーターの読み込み
calcDsp; // 計算表示
end;
procedure TForm1.Button3Click(Sender: TObject);
var
check : integer;
begin
val(LabeledEdit1.Text, nd, check);
if check <> 0 then exit;
if nd <> 5 then exit;
setlength(data , nd, 2); // 配列確保
{ for JJ := 0 to nd -1 do // データークリア
begin
for II := 0 to 1 do
data[JJ, II] := 0;
end;}
StrinGridset; // データー表示
end;
procedure TForm1.Button4Click(Sender: TObject);
var
Check,JJ: integer;
Dataind: double;
begin
// if nd <> unknowns then exit;
for JJ := 0 to nd - 1 do
begin
val(stringGrid1.Cells[1,JJ + 1], Dataind, Check);
if Check = 0 then data[JJ, 0] := Dataind
else data[JJ, 0] := 0;
val(stringGrid1.Cells[2,JJ + 1], Dataind, Check);
if Check = 0 then data[JJ, 1] := Dataind
else data[JJ, 1] := 0;
end;
calcDsp; // 計算表示
end;
end.