楕円同士の接線
楕円同士の接線を求めるのには、二つの楕円と、楕円の接線の連立方程式が解ければ良いのですが、半径比が異なり、角度を持っている楕円同士の場合難しいので、楕円外の点と楕円の接線の計算を、二つの楕円で交互に行う事により実現します。
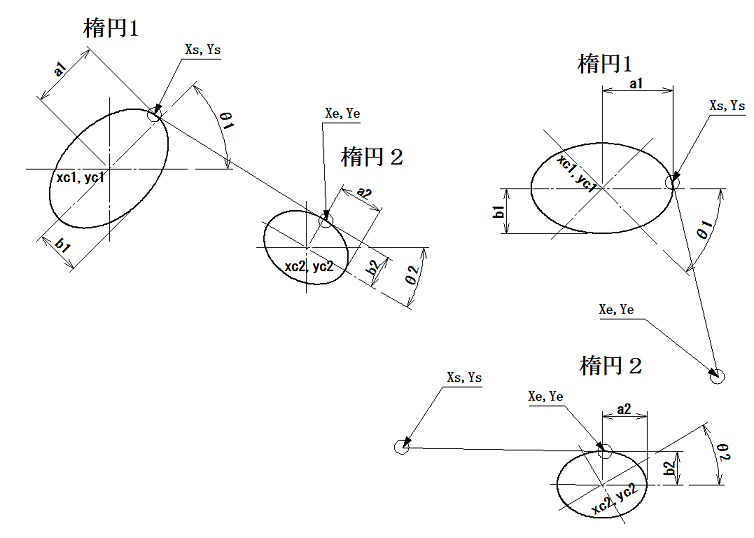最初に、楕円１と楕円２に、仮の接点の位置、Ｘｓ，Ｙｓ Ｘｅ，Ｙｅをそれぞれ与えます。
次に、楕円１に対する、座標Ｘｅ，Ｙｅからの接線の接点Ｘｓ，Ｙｓの座標を計算しなおします。
更に、今度は、楕円２に対する、座標Ｘｓ，Ｙｓからの接線の接点Ｘｅ，Ｙｅを計算します。
この計算を繰り返し、接点の位置が変化しなくなるまで行うことにより、接点と接線を求めます。
数回の繰り返しで、計算は収束します。
楕円は、傾きを持っているので、それぞれの楕円の計算時、原点への移動と、傾きの無いように座標変換を行い計算を行います。
実際の計算
左図、角度θの楕円上座標Ｘθ、Ｙθを求めるのは、接線の計算とは直接は関係ありません。
マウスで、楕円上の仮の接点の位置を与えるのに利用しています。
接点の計算に使用しているのは、左図下側の楕円外の点Ｘｐ，Ｙｐを通る接線です。
楕円外の指定点を通る接線を求める時、楕円のまゝで計算するのは困難なので、円に変換をしてから、接点を求め、楕円の座標に戻して計算します。
ここでは、直線の方程式は求めていません。
２点が与えられるので、簡単に直線の方程式は求めることができます。
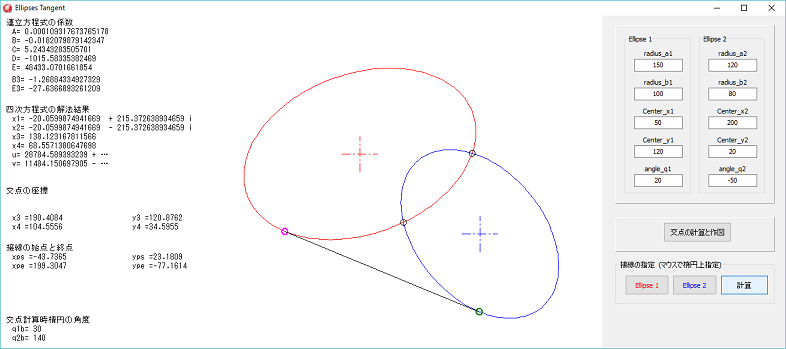左図は、接点を求めるプログラムの実行例です。
新たに、専用のプログラムを作成するのは面倒なので、楕円同士の交点を計算するプログラムに接線の接点を求める計算を追加しました。
交点の位置と、接線の計算は無関係です。
最初に、楕円の作図を行い、次に、楕円１と楕円２の仮の接点の位置を指定します。
仮の位置の指定は、マウスで楕円の線上の近辺をクリックすることにより行います。
指定が終わったら、計算ボタンをクリックすることにより、接点と接線が表示されます。
指定された位置によっては、計算が出来ないことがあります、その場合は改めて指定をし直します。
接点の計算時、接点は２個計算されますが、指定された位置と近い方の接点の位置を採用しています。
プログラム
unit Tangent_Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.ExtCtrls, Vcl.StdCtrls, Vcl.Buttons, math;
type
TForm1 = class(TForm)
Panel1: TPanel;
Ellipse1Box: TGroupBox;
radius_a1_Edit: TLabeledEdit;
radius_b1_Edit: TLabeledEdit;
Center_x1_Edit: TLabeledEdit;
Center_y1_Edit: TLabeledEdit;
angle_q1_Edit: TLabeledEdit;
Ellipse2Box: TGroupBox;
radius_a2_Edit: TLabeledEdit;
radius_b2_Edit: TLabeledEdit;
Center_x2_Edit: TLabeledEdit;
Center_y2_Edit: TLabeledEdit;
angle_q2_Edit: TLabeledEdit;
Panel2: TPanel;
SelectBtn: TBitBtn;
Image1: TImage;
Image2: TImage;
GroupBox1: TGroupBox;
CalcBtn: TButton;
StartPosBtn: TBitBtn;
EndPosBtn: TBitBtn;
procedure FormCreate(Sender: TObject);
procedure SelectBtnClick(Sender: TObject);
procedure Image1MouseUp(Sender: TObject; Button: TMouseButton; Shift: TShiftState; X,
Y: Integer);
procedure StartPosBtnClick(Sender: TObject);
procedure EndPosBtnClick(Sender: TObject);
procedure CalcBtnClick(Sender: TObject);
private
{ Private 宣言 }
procedure imageClear;
function Dist(x1, y1, x2, y2 : double): double;
function Angle(dx, dy: double): double;
procedure LineSub(Tcv: TCanvas; px1, py1, px2, py2: double);
procedure pitchControl(NLine, LW: integer);
procedure LineSubPitch(Tcv : TCanvas; Ln: integer; var i: integer; var d1: double; px1, py1, px2, py2:double);
function angleSe(a, b, rad: double): double;
procedure EllipseEx(Tcv: TCanvas; h, lf, lw: integer; lc: Tcolor; a, b, x, y, rq, sq, eq: double);
procedure quadratic_transform(a, b, x, y, qdeg: double; var A0, B0, C0, D0, E0, F0: double);
procedure inputdata_drawing;
function cross_calc: boolean;
function cross_quadratic(a, b, c, d, e: double; var x1, x2, x3, x4: double): byte;
procedure trance(Xn, Yn, defQ, xo1, yo1: double; var x, y: double);
procedure StraightLineDraw(Tcv: TCanvas; h, lf, lw: integer; lc: Tcolor; xs, ys, xe, ye: double; sf: boolean);
procedure TaninputDraw;
procedure Position_Calc;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
const
PitchN = 5; // 線ピッチ設定数
LineN = 3; // 線種数
LIMIT8 = 0.00000001;
MINIMAM = 1E-13;
type
TLinePitch = Record // 線種用レコード
Pitch : array[0..PitchN] of double; // ピッチ 線長さ 空白の繰り返し
segment : integer; // ピッチ数
End;
var
LPitch : array of TLinePitch; // 線種用 (線ピッチ)
VPitch : array[0..PitchN] of double; // 線幅による線ピッチ設定用
magnification : double;
ar1, ar2 : double;
br1, br2 : double;
xo1, xo2 : double;
yo1, yo2 : double;
q1, q2 : double;
scale : double;
shift_x : double;
shift_y : double;
d01 : double;
d0p : integer;
posXs : double; // 接線始点指定位置X
posYs : double; // 接線始点指定位置y
posXe : double; // 接線終点指定位置X
posYe : double; // 接線終点指定位置y
TanmodF : byte; // bit0 始点指定 bit1 終点位置 bit2 計算
TandrwF : byte; // bit0 始点指定 bit1 終点位置 bit2 交点計算済み 描画
const
draw_margin = 30; // 左右上下作図マージン
procedure TForm1.imageClear;
begin
image1.Canvas.Brush.Style := bsSolid;
image1.Canvas.Brush.Color := clWhite;
image1.Canvas.FillRect(Rect(0, 0, image1.Width, image1.Height));
image2.Canvas.Brush.Style := bsSolid;
image2.Canvas.Brush.Color := clWhite;
image2.Canvas.FillRect(Rect(0, 0, image2.Width, image2.Height));
end;
//-----------------------------------------------
// 線幅によるピッチの補正
// 線幅を広くするとスペースが狭くなるので広げます
// NLine 線種
// LW 線幅
//-----------------------------------------------
procedure TForm1.pitchControl(NLine, LW: integer);
var
i : integer;
begin
// 線幅によるピッチの補正
for i := 0 to pitchN do begin
if i mod 2 <> 0 then // 奇数配列noセグメントがスペース
Vpitch[i] := LPitch[NLine].Pitch[i] + LW // スペースに線幅加算
else
Vpitch[i] := LPitch[NLine].Pitch[i];
end;
end;
//----------------------------
// 作図用 二点間線引き
//----------------------------
procedure TForm1.LineSub(Tcv: TCanvas; px1, py1, px2, py2: double);
var
x1, y1, x2, y2 : integer ;
begin
x1 := Round(px1);
y1 := Round(py1);
x2 := Round(px2);
y2 := Round(py2);
Tcv.MoveTo(x1, y1);
Tcv.LineTo(x2, y2);
end;
//----------------------
// 距離（長さ）を計算
// x1, y1 : 始点
// x2, y2 : 終点
// out : 距離(長さ)
//----------------------
function TForm1.Dist(x1, y1, x2, y2 : double): double;
begin
Result := Sqrt((x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1)) ;
end;
//--------------------------------
// 角度を計算[rad]
// dx : X方向差分
// dy : Y方向差分
// out: 角度 (0～2 * Pi)
//--------------------------------
function TForm1.Angle(dx, dy: double): double ;
var
r : double ;
begin
Result := 0.0;
if (Abs(dx) < LIMIT8) and (Abs(dy) < LIMIT8) then exit;
r := ArcTan2(dy, dx);
if r < 0.0 then r := r + 2.0 * Pi;
Result := r;
end;
//--------------------------------------
// 線分の表示・サブ２：線種指定
// Ln : 線種番号(1-)
// i : 開始セグメント番号(終了時更新)
// d1 : 開始ピッチ長さ (終了時更新)
// px1, py1 : 線分始点[mm]
// px2, py2 : 線分終点[mm]
//--------------------------------------
procedure TForm1.LineSubPitch(Tcv: TCanvas; Ln: integer; var i: integer; var d1: double; px1, py1, px2, py2:double);
var
x1, y1, x2, y2 : double;
a, sa, ca, d, p : double;
PenStyle : TPenstyle;
begin
PenStyle := Tcv.Pen.Style; // 線種バックアップ
Tcv.Pen.Style := psSolid;
if (Ln < 0) or (Ln >= LineN) then begin // 無い線種は実線
LineSub(Tcv, px1, py1, px2, py2);
Tcv.Pen.Style := PenStyle; // 線種戻し
exit;
end;
a := Angle(px2 - px1, py2 - py1); // 角度計算
d := Dist(px1, py1, px2, py2); // 距離計算
ca:= Cos(a); // コサイン
sa:= Sin(a); // サイン
x1:= px1; // 始点x
y1:= py1 ; // 始点y
repeat
p := Vpitch[i] - d1; // ピッチと開始ピッチ長さ差分 残り分
if (p > d) then p := d; // 距離より残り分が大きい場合 距離
x2 := x1 + p * ca ; // 新しい位置計算
y2 := y1 + p * sa ;
if (i mod 2) = 0 then // セグメント偶数毎に線引き 空白部線引きしない
LineSub(Tcv, x1, y1, x2, y2);
x1 := x2; // 終点を始点にセット
y1 := y2;
d := d - p ; // 残り長さ計算
if d > LIMIT8 then begin // 残り長さがあったら
d1 := 0.0; // 開始ピッチ長さクリア
Inc(i); // セグメントカウンターインクリメント
if i >= LPitch[Ln].segment then i := 0; // セグメント数を超えたらゼロに戻し
end;
until d <= LIMIT8;
d1 := d1 + p; // 開始ピッチ長さ
Tcv.Pen.Style := PenStyle; // 線種戻し
end;
//------------------------------------------
// 楕円の開始角を 基礎円の開始角に変換
//------------------------------------------
function TForm1.angleSe(a, b, rad: double): double;
const
KMIN = 0.00000001;
var
l : double;
begin
// 90°, 270°, 0°, 180° 360°近傍は計算しない
if (abs(rad - pi / 2) < KMIN) or (abs(rad - pi - pi / 2) < KMIN)
or (abs(rad) < KMIN) or (abs(rad - pi) < KMIN) or
(abs(rad - pi * 2) < KMIN)
then begin
result := rad;
exit;
end;
// 底辺の長さ計算 ( b / a の値がいつも正の値なので元の角度によって角度を補正)
// 分母がゼロに近くなる時もあるので、判別が不要なarctan2を使用します
l := b / a / tan(rad);
// 180°以下だったら
if rad < pi then
result := arctan2(1, l)
else
// 360°以下だったら
if rad < pi * 2 then
result := arctan2(1, l) + pi
// 360°を超えていたら
else
result := arctan2(1, l) + pi * 2;
end;
//-------------------------------------------------------------
// 直線の描画
// 直線の開始はsfをTrueにします。
// つながった直線、折れ線を描画する場合は、sfをFalseに
//-------------------------------------------------------------
procedure TForm1.StraightLineDraw(Tcv: TCanvas; h, lf, lw: integer; lc: Tcolor; xs, ys, xe, ye: double; sf: boolean);
begin
Tcv.Pen.Width := lw;
Tcv.Pen.Color := lc;
// 線幅によるピッチの補正
pitchControl(lf, lw);
// y方向変換
ys := h - ys;
ye := h - ye;
if sf then begin
d01 := 0;
d0p := 0;
end;
LineSubPitch( // ピッチ線描画
tcv, // TCanvas
lf, // 線種
d0p, // セグメント位置
d01, // 長さ
xs, // 始点X
ys, // 始点Y
xe, // 終点X
ye // 終点Y
);
end;
//---------------------------------------
// 楕円の描画
// Windows為ののy方向変換は,このルーチンで行います。
// tcv 描画キャンバスの指定
// h キャンバスの高さ
// lf 線の種類
// lw 線の幅
// lc 線の色
// a 半径a
// b 半径b
// x 中心位置 x
// y 中心位置 y
// rq 楕円の角度
// sq 描画開始角
// eq 描画終了
//---------------------------------------
procedure TForm1.EllipseEx(Tcv : TCanvas; h, lf, lw: integer; lc: Tcolor; a, b, x, y, rq, sq, eq: double);
var
sqrad, eqrad : double;
qrad : double;
Ssqrad, Seqrad : double;
sp : integer;
dq : double;
d1 : double;
dp : integer;
xf, yf : double;
rdist, nrad : double;
px1, py1 : double;
px2, py2 : double;
i : integer;
begin
Tcv.Pen.Width := lw;
Tcv.Pen.Color := lc;
// y方向変換
y := h - y;
// 線幅によるピッチの補正
pitchControl(lf, lw);
// 終了角と開始角が一致したら全周
if abs(sq - eq) < LIMIT8 then begin
sq := 0;
eq := 360;
end;
// 分割数 半径に応じて調整
sp := round(sqrt(a + b) * 4); // 分割数
// 楕円の計算と描画
sqrad := sq / 180 * pi;
eqrad := eq / 180 * pi;
qrad := pi / 180 * rq; // 回転角 ラジアン
Ssqrad := angleSe(a, b, sqrad); // 基本円角度に変換
Seqrad := angleSe(a, b, eqrad); // 基本円角度に変換
// 分割微小角計算 分割数角度で補正
if Seqrad >= Ssqrad then begin
sp := round(sp * (Seqrad - Ssqrad) / pi);
if sp < 1 then sp := 1;
dq := (Seqrad - Ssqrad) / sp // 分割微小角 ラジアン
end
else begin
sp := round(sp * (Pi * 2 - Ssqrad + Seqrad) / pi);
if sp < 1 then sp := 1;
dq := (Pi * 2 - Ssqrad + Seqrad) / sp; // 分割微小角 ラジアン
end;
// 開始点の計算
d1 := 0; // 長さ
dp := 0; // セグメント位置
xf := cos(Ssqrad) * a; // 基本楕円座標X スタート座標
yf := sin(Ssqrad) * b; // 基本楕円座標y スタート座標
nrad := arctan2(yf, xf) + qrad; // 新しい角度 回転角加算
rdist := sqrt(xf * xf + yf * yf); // 中心と楕円座標の距離
px1 := cos(nrad) * rdist + x; // 開始座標X
py1 := sin(nrad) * -rdist + y; // 開始座標Y -rdistはY座標反転の為
// WindowはY座標方向が逆のため
// 分割数分計算繰り返し描画
for i := 1 to sp do begin
xf := cos(Ssqrad + dq * i) * a;
yf := sin(Ssqrad + dq * i) * b;
nrad := arctan2(yf , xf) + qrad;
rdist := sqrt(xf * xf + yf * yf);
px2 := round(cos(nrad) * rdist + x); // 終点座標X
py2 := round(sin(nrad) * -rdist + y); // 終点座標Y
// ピッチ線描画
LineSubPitch( // ピッチ線描画
tcv, // TCanvas
lf, // 線種
dp, // セグメント位置
d1, // 長さ
px1, // 始点X
py1, // 始点Y
px2, // 終点X
py2 // 終点Y
);
px1 := px2; // 終点Xを始点Xに
py1 := py2; // 終点Yを始点Yに
end;
end;
//-------------------------------------------------
// 楕円の方程式 二次方程式への変換
// AX^2 + BXY + CY^2 + DX + EY + F の A,B,C,D,E,F
//-------------------------------------------------
procedure TForm1.quadratic_transform(a, b, x, y, qdeg: double; var A0, B0, C0, D0, E0, F0: double);
var
Q : double;
sin_Q, cos_q : double;
ah2, bh2 : double;
sinh2, cosh2 : double;
sincosQ : double;
xh2, yh2, xy : double;
begin
Q := qdeg / 180 * pi; // ラジアン単位に変換
sin_Q := sin(Q);
cos_Q := cos(Q);
ah2 := a * a;
bh2 := b * b;
sinh2 := sin_Q * sin_Q;
cosH2 := cos_Q * cos_Q;
sincosQ := sin_Q * cos_Q;
xh2 := x * x;
yh2 := y * y;
xy := x * y;
A0 := cosh2 / ah2 + sinh2 / bh2;
B0 := 2 * (1 / ah2 - 1 / bh2) * sincosQ;
C0 := sinh2 / ah2 + cosh2 / bh2;
D0 := -2 * ((x * cosh2 + y * sincosQ) / ah2 + (x * sinh2 - y * sincosQ) / bh2);
E0 := -2 * ((x * sincosQ + y * sinh2) / ah2 + (y * cosh2 - x * sincosQ) / bh2);
F0 := (xh2 * cosh2 + 2 * xy * sincosQ + yh2 * sinh2) / ah2
+ (xh2 * sinh2 - 2 * xy * sincosQ + yh2 * cosh2) / bh2
- 1;
end;
//-----------------------------------------------------
// 四次 二次方程式の解法 デカルトの方法
// ax^4 + bx^3 + cx^2 + dx + e = 0
// x の 値は 4個
// 虚数にならない X を フラグにして byteで返します
// x1 bit0 x2 bit1 x3 bit2 x4 bit3
//-----------------------------------------------------
function TForm1.cross_quadratic(a, b, c, d, e: double; var x1, x2, x3, x4: double): byte;
const
IMAGIMIN = 1E-8;
var
A3, A2, A1, A0 : double;
b2, b1, b0 : double;
f0 : double;
e1, e0, e1s3, e0s2, e02s4, e13s27 : double;
e02s4pe13s27 : double;
r, rh1s3, cosQ, Q, cosQs3, sinQs3 : double;
u, v, wiupv, t, c1, c0 : double;
up, vm : string;
d1, d0, c1h2s4mc0, d1h2s4md0 : double;
xim1, xim2, xim3, xim4 : string;
b2h2mb0 : double;
ru, rv, ruh1s3, rvh1s3 : double;
Qu, Qv, Qus3, Qvs3 : double;
u1, u2, u3, v1, v2, v3 : double;
u1pv1, u2pv3, u3pv2 : double;
u1S, u2S, u3S, v1S, v2S, v3S : double;
u1pv1S, u2pv3S, u3pv2S : double;
rs1, rs2, rs3, rs4 : byte;
ii : integer;
begin
Result := 0;
u := 0;
v := 0;
if (abs(a) > MINIMAM) then begin
// a=0 の場合は四次方程式でないので解法不可
// x^4 + A3x^3 + A2x^2 + A1x + A0 = 0 に変換
A3 := b / a;
A2 := c / a;
A1 := d / a;
A0 := e / a;
// 四次式の解法
b2 := -3 / 8 * A3 * A3 + A2;
b1 := A3 * A3 * A3 / 8 - A3 * A2 / 2 + A1;
b0 := -3 / 256 * A3 * A3 * A3 * A3 + A3 * A3 * A2 / 16 - A3 * A1 / 4 + A0;
e1 := -b2 * b2 / 3 - 4 * b0;
e0 := -2 / 27 * b2 * b2 * b2 + 8 / 3 * b2 * b0 - b1 * b1;
e1s3 := e1 / 3;
e0s2 := e0 / 2;
e02s4 := e0s2 * e0s2;
e13s27 := e1s3 * e1s3 * e1s3;
e02s4pe13s27 := e02s4 + e13s27; // 判別式
t := b2 * b2 - 4 * b0; // 判別式2
if (b1 <> 0) or (t < 0) then begin
if e02s4pe13s27 >= 0 then begin
u := -e0 / 2 + sqrt(e02s4pe13s27);
if u < 0 then begin // 負数の立方根対策
u := power(-u, 1/3);
u := -u;
end
else u := power(u, 1/3);
v := -e0 / 2 - sqrt(e02s4pe13s27);
if v < 0 then begin // 負数の立方根対策
v := power(-v, 1/3);
v := -v;
end
else v := power(v, 1/3);
wiupv := u + v;
end
else begin
r := sqrt(e02s4 + ABS(e02s4pe13s27)); // r > 0 e02s4 は必ずプラスかゼロなのでゼロ以下は無し
rh1s3 := power(r , 1/3);
if r <> 0 then begin
cosQ := -e0s2 / r;
Q := arccos(cosQ);
cosQs3 := cos(Q / 3);
sinQs3 := sin(Q / 3);
wiupv := 2 * rh1s3 * cosQs3;
u := rh1s3 * cosQs3;
v := u;
end
else
wiupv := 0;
end;
t := wiupv - 2 / 3 * b2; // t > 0
if t < 0 then t := 0; // 基本的に t >= 0 t < 0 時は桁落ちの影響
c1 := sqrt(t);
if c1 <> 0 then c0 := (c1 * c1 * c1 + b2 * c1 - b1) / 2 / c1
else
if b2 * b2 - 4 * b0 > 0 then
c0 := (b2 + sqrt(b2 * b2 - 4 * b0)) / 2
else
c0 := b2 / 2;
d1 := - c1;
d0 := b0 / c0;
end
else begin
c1 := 0;
c0 := (b2 + sqrt(t)) / 2;
d1 := 0;
d0 := (b2 - sqrt(t)) / 2;
end;
if e02s4pe13s27 < 0 then begin
up := floatTostr(rh1s3 * sinQs3) + ' i'; // 複素数処理 textに変換
vm := floatTostr(rh1s3 * sinQs3) + ' i'; // 複素数処理 textに変換
end
else begin
up := '…';
vm := '…';
end;
c1h2s4mc0 := c1 * c1 / 4 - c0;
d1h2s4md0 := d1 * d1 / 4 - d0;
if abs(c1h2s4mc0) < IMAGIMIN then c1h2s4mc0 := 0; // 計算誤差修正
if abs(d1h2s4md0) < IMAGIMIN then d1h2s4md0 := 0; // 微小な複素数は許容
if c1h2s4mc0 >=0 then begin
x1 := -c1 / 2 - A3 / 4 + sqrt(c1h2s4mc0); // x1
xim1 := '';
Result := Result or 1;
x2 := -c1 / 2 - A3 / 4 - sqrt(c1h2s4mc0); // x2
xim2 := '';
Result := Result or 2;
end
else begin
x1 := -c1 / 2 - A3 / 4; // x1
xim1 := ' + ' + floatTostr(sqrt(-c1h2s4mc0)) + ' i'; // 複素数処理 textに変換
x2 := -c1 / 2 - A3 / 4; // x2
xim2 := ' - ' + floatTostr(sqrt(-c1h2s4mc0)) + ' i'; // 複素数処理 textに変換
end;
if d1h2s4md0 >=0 then begin
x3 := -d1 / 2 - A3 / 4 + sqrt(d1h2s4md0); // x3
xim3 := '';
Result := Result or 4;
x4 := -d1 / 2 - A3 / 4 - sqrt(d1h2s4md0); // x4
xim4 := '';
Result := Result or 8;
end
else begin
x3 := -d1 / 2 - A3 / 4; // x3
xim3 := ' + ' + floatTostr(sqrt(-d1h2s4md0)) + ' i'; // 複素数処理 textに変換
x4 := -d1 / 2 - A3 / 4; // x4
xim4 := ' - ' + floatTostr(sqrt(-d1h2s4md0)) + ' i'; // 複素数処理 textに変換
end;
image2.Canvas.TextOut(10, 150,'四次方程式の解法結果');
image2.Canvas.TextOut(20, 165,'x1= ' + floattostr(x1) + ' ' + xim1);
image2.Canvas.TextOut(20, 180,'x2= ' + floattostr(x2) + ' ' + xim2);
image2.Canvas.TextOut(20, 195,'x3= ' + floattostr(x3) + ' ' + xim3);
image2.Canvas.TextOut(20, 210,'x4= ' + floattostr(x4) + ' ' + xim4);
image2.Canvas.TextOut(20, 225, 'u= ' + floattostr(u) + ' + ' + up);
image2.Canvas.TextOut(20, 240, 'v= ' + floattostr(v) + ' - ' + vm);
end;
if (abs(a) <= MINIMAM) and (abs(c) > MINIMAM) then begin
// 二次方程式の解法
a0 := C;
b0 := D;
c0 := E;
f0 := b0 * b0 - 4 * a0 * c0;
if abs(f0) < 1E-8 then f0 := 0;
if f0 >= 0 then begin
X1 := (-b0 + sqrt(f0)) / 2 / a0;
X2 := (-b0 - sqrt(f0)) / 2 / a0;
result := 1 + 2;
end
else begin
x1 := -b0 / a0 / 2;
x2 := x1;
xim1 := floattostr(sqrt(abs(f0))) + ' i';
xim2 := floattostr(- sqrt(abs(f0))) + ' i';
end;
with image2.Canvas do begin
TextOut(10, 150,'二次方程式の解法結果');
TextOut(20, 165,'x1= ' + floattostr(x1) + ' ' + xim1);
TextOut(20, 180,'x2= ' + floattostr(x2) + ' ' + xim2);
end;
end;
end;
// 座標変換されているので元の座標にも戻します
procedure TForm1.trance(Xn, Yn, defQ, xo1, yo1: double; var x, y: double);
var
xh, yh : double;
stn : double;
Q, Q1 : double;
begin
Xn := Xn / scale;
Yn := Yn / scale;
Q := arctan2(Yn, Xn);
Q1 := Q - defQ;
stn := sqrt(xn * xn + yn * yn);
xh := cos(Q1) * stn;
yh := sin(Q1) * stn;
x := xh + xo1;
y := yh + yo1;
end;
//------------------------------------
// 二つの楕円の交点計算
//------------------------------------
function TForm1.cross_calc: boolean;
const
Ftop = 300;
trnQ = 30;
k180 = 180;
k90 = 90;
var
x1, x2, x3, x4 : double;
y1, y2, y3, y4 : double;
A1, B1, C1, D1, E1, F1 : double;
A2, B2, C2, D2, E2, F2 : double;
A3, B3, D3, E3, F3 : double;
A, B, C, D, E : double;
xflag : byte;
dfq, qb, qn : double;
nx, ny : double;
stn : double;
sq, tmq : double;
df1, df2 : double;
xob, yob : double;
q1b, q2b : double;
begin
// 座標変換 楕円１又は 楕円２の角度が30度になるようにして計算します。
// 片方が円でもう一方が楕円の時、楕円の角度が 0, 90, 180, 270 度にある時
// 方程式の解法が正しくできません。
// その時は、楕円の角度が30°になるように座標変換をして計算します
if ar1 > br1 then df1 := br1 / ar1
else df1 := ar1 / br1;
if ar2 > br2 then df2 := br2 / ar2
else df2 := ar2 / br2;
if df1 <= df2 then tmq := q1
else tmq := q2;
// q1又はq2の角度から、0～90どの範囲の角度にします
// 補正角度を小さくするためです
repeat
if tmq >= k90 then tmq := tmq - k90;
if tmq < 0 then tmq := tmq + k90;
until (tmq >= 0) and (tmq < k90);
// 30度との角度差
sq := trnQ - tmq;
nx := xo2 - xo1;
ny := yo2 - yo1;
// 楕円１と２の位置の角度補正
dfq := sq /180 * pi;
qb := arctan2(ny, nx);
qn := qb + dfq;
// 楕円１と２の角度補正
q2b := q2 + sq;
q1b := q1 + sq;
// 0～180°の範囲になるように修正
repeat
if q2b >= k180 then q2b := q2b - k180;
if q2b < 0 then q2b := q2b + k180;
until (q2b < k180) and (q2b >= 0);
repeat
if q1b >= k180 then q1b := q1b - k180;
if q1b < 0 then q1b := q1b + k180;
until (q1b < k180) and (q1b >= 0);
// 楕円２の新しい座標計算
stn := sqrt(nx * nx + ny * ny);
xob := cos(qn) * stn * scale;
yob := sin(qn) * stn * scale;
// 楕円式の変換
quadratic_transform(ar1 * scale, br1 * scale, 0, 0, q1b, A1, B1, C1, D1, E1, F1);
quadratic_transform(ar2 * scale, br2 * scale, xob, yob, q2b, A2, B2, C2, D2, E2, F2);
// y^2 の消去
A3 := A1 / C1 - A2 / C2;
B3 := B1 / C1 - B2 / C2;
D3 := D1 / C1 - D2 / C2;
E3 := E1 / C1 - E2 / C2;
F3 := F1 / C1 - F2 / C2;
// 四次式の係数を求めます
// Ax^4 + Bx^3 + Cx^2 + Dx + E = 0;
A := A1*B3*B3 - A3*B1*B3 + A3*A3*C1;
B := 2*A1*B3*E3 + 2*A3*C1*D3 + B3*B3*D1 - A3*B1*E3 - B1*B3*D3 - A3*B3*E1;
C := A1*E3*E3 + 2*A3*C1*F3 + D3*D3*C1 + 2*B3*D1*E3 + B3*B3*F1 - B1*B3*F3
- B1*D3*E3 - A3*E1*E3 - B3*D3*E1;
D := 2*C1*D3*F3 + D1*E3*E3 + 2*B3*E3*F1 - B3*E1*F3 - D3*E1*E3 - B1*E3*F3;
E := C1*F3*F3 + E3*E3*F1 - E1*E3*F3;
image2.Canvas.Brush.Style := bsClear;
// 連立方程式の係数表示
image2.Canvas.TextOut(10, 5, '連立方程式の係数');
image2.Canvas.TextOut(20, 20, 'A= ' + floatTostr(A));
image2.Canvas.TextOut(20, 35, 'B= ' + floatTostr(B));
image2.Canvas.TextOut(20, 50, 'C= ' + floatTostr(C));
image2.Canvas.TextOut(20, 65, 'D= ' + floatTostr(D));
image2.Canvas.TextOut(20, 80, 'E= ' + floatTostr(E));
image2.Canvas.TextOut(20, 100, 'B3= ' + floatTostr(B3));
image2.Canvas.TextOut(20, 115, 'E3= ' + floatTostr(E3));
image2.Canvas.TextOut(10, 500, '交点計算時楕円の角度');
image2.Canvas.TextOut(20, 515, 'q1b= ' + floatTostr(q1b));
image2.Canvas.TextOut(20, 530, 'q2b= ' + floatTostr(q2b));
result := false;
xflag := 0;
// 連立方程式の解放を行い x の値を計算 x の値から
// y の値を求めます 分母がゼロ場合は計算しません 分母 B3x + E3
// 四次 二次式の解法
if (b3 <> 0) or (E3 <> 0) then
xflag := cross_quadratic(a, b, c, d, e, x1, x2, x3, x4);
// y の値を求めます x が虚数の場合は計算しません
// B3x + E3 がゼロより大きい場合は四次方程式作成に利用した
// yの値を求める式でyの値を計算します
// 楕円の角度を30°にすることにより分母が０になることを防止しています
if xflag <> 0 then begin
if xflag and 1 = 1 then begin
if abs(B3 * x1 + E3) > 0 then
y1 := - (A3 * x1 * x1 + D3 * x1 + F3) / (B3 * x1 + E3)
else xflag := xflag and ($FF - 1);
end;
if xflag and 2 = 2 then begin
if abs(B3 * x2 + E3) > 0 then
y2 := - (A3 * x2 * x2 + D3 * x2 + F3) / (B3 * x2 + E3)
else xflag := xflag and ($FF - 2);
end;
if xflag and 4 = 4 then begin
if abs(B3 * x3 + E3) > 0 then
y3 := - (A3 * x3 * x3 + D3 * x3 + F3) / (B3 * x3 + E3)
else xflag := xflag and ($FF - 4);
end;
if xflag and 8 = 8 then begin
if abs(B3 * x4 + E3) > 0 then
y4 := - (A3 * x4 * x4 + D3 * x4 + F3) / (B3 * x4 + E3)
else xflag := xflag and ($FF - 8);
end;
end
else result := true;
// 計算結果の表示 座標は元の座標に戻します
image2.Canvas.TextOut( 10,Ftop - 15 ,'交点の座標');
if xflag and 1 = 1 then begin
trance(X1, Y1, dfQ, xo1, yo1, x1, y1); // 座標変換 元の座標に戻します
image2.Canvas.TextOut( 20,Ftop ,'x1 =' + floatTostrF(x1,ffFixed,10,4));
image2.Canvas.TextOut(220,Ftop ,'y1 =' + floatTostrF(y1,ffFixed,10,4));
end;
if xflag and 2 = 2 then begin
trance(X2, Y2, dfQ, xo1, yo1, x2, y2);
image2.Canvas.TextOut( 20,Ftop+15,'x2 =' + floatTostrF(x2,ffFixed,10,4));
image2.Canvas.TextOut(220,Ftop+15,'y2 =' + floatTostrF(y2,ffFixed,10,4));
end;
if xflag and 4 = 4 then begin
trance(X3, Y3, dfQ, xo1, yo1, x3, y3);
image2.Canvas.TextOut( 20,Ftop+30,'x3 =' + floatTostrF(x3,ffFixed,10,4));
image2.Canvas.TextOut(220,Ftop+30,'y3 =' + floatTostrF(y3,ffFixed,10,4));
end;
if xflag and 8 = 8 then begin
trance(X4, Y4, dfQ, xo1, yo1, x4, y4);
image2.Canvas.TextOut( 20,Ftop+45,'x4 =' + floatTostrF(x4,ffFixed,10,4));
image2.Canvas.TextOut(220,Ftop+45,'y4 =' + floatTostrF(y4,ffFixed,10,4));
end;
// 交点丸表示
if xflag and 1 = 1 then
EllipseEx(image1.Canvas,
image1.Height,
3,
1,
clblack,
5,
5,
(x1 - shift_x) * magnification + draw_margin,
(y1 - shift_y) * magnification + draw_margin,
0,
0,
360);
if xflag and 2 = 2 then
EllipseEx(image1.Canvas,
image1.Height,
3,
1,
clblack,
5,
5,
(x2 - shift_x) * magnification + draw_margin,
(y2 - shift_y) * magnification + draw_margin,
0,
0,
360);
if xflag and 4 = 4 then
EllipseEx(image1.Canvas,
image1.Height,
3,
1,
clblack,
5,
5,
(x3 - shift_x) * magnification + draw_margin,
(y3 - shift_y) * magnification + draw_margin,
0,
0,
360);
if xflag and 8 = 8 then
EllipseEx(image1.Canvas,
image1.Height,
3,
1,
clblack,
5,
5,
(x4 - shift_x) * magnification + draw_margin,
(y4 - shift_y) * magnification + draw_margin,
0,
0,
360);
end;
//--------------------------------------------------------
// 入力された楕円の描画
// 楕円作図のy方向は、楕円作図ルーチンで修正されます。
//--------------------------------------------------------
procedure TForm1.inputdata_drawing;
var
left_min, left_max : double;
top_min, top_max : double;
all_width, all_height : double;
ac1, ac2 : double;
x1, x2, y1, y2 : double;
begin
// 楕円の半径の大きい方選択
ac1 := ar1;
if ar1 < br1 then begin
ac1 := br1;
end;
ac2 := ar2;
if ar2 < br2 then begin
ac2 := br2;
end;
// 半径を一定の値で計算する為のスケール設定
// CONTRの値を変更した場合は、四次二次連立方程式の判別値 MINIMAM4, MINIMAM2 も変更する必要があります。
if ac2 > ac1 then scale := CONTR / ac2
else scale := CONTR / ac1;
// 作図範囲の設定
left_min := xo1 - ac1;
if xo2 - ac2 < left_min then left_min := xo2 - ac2;
left_max := xo1 + ac1;
if xo2 + ac2 > left_max then left_max := xo2 + ac2;
all_width := left_max - left_min;
top_min := yo1 - ac1;
if yo2 - ac2 < top_min then top_min := yo2 - ac2;
top_max := yo1 + ac1;
if yo2 + ac2 > top_max then top_max := yo2 + ac2;
all_height := top_max - top_min;
top_max := (image1.Height - draw_margin * 2) / all_Height;
magnification := (image1.Width - draw_margin * 2) / all_width;
if magnification > top_max then magnification := top_max;
shift_x := left_min;
shift_y := top_min;
// イメージクリア
imageClear;
// 楕円作図
x1 := (xo1 - left_min) * magnification + draw_margin;
y1 := (yo1 - top_min) * magnification + draw_margin;
x2 := (xo2 - left_min) * magnification + draw_margin;
y2 := (yo2 - top_min) * magnification + draw_margin;
EllipseEx(image1.Canvas,
image1.Height, // canvas高さ
3, // 線種
1, // 線幅
clRed, // 色
ar1 * magnification, // 半径a
br1 * magnification, // 半径b
x1, // 中心位置x
y1, // 中心位置y
q1, // 回転角 deg
0, // 作図開始角
360); // 作図終了角
// 楕円２作図
EllipseEx(image1.Canvas,
image1.Height,
3,
1,
clBlue,
ar2 * magnification,
br2 * magnification,
x2,
y2,
q2,
0,
360);
StraightLineDraw(image1.Canvas, image1.Height, 1, 1, clRed, x1 - 30, y1, x1 + 30, y1, true);
StraightLineDraw(image1.Canvas, image1.Height, 1, 1, clRed, x1, y1 - 30, x1, y1 + 30, true);
StraightLineDraw(image1.Canvas, image1.Height, 1, 1, clBlue, x2 - 30, y2, x2 + 30, y2, true);
StraightLineDraw(image1.Canvas, image1.Height, 1, 1, clBlue, x2, y2 - 30, x2, y2 + 30, true);
end;
procedure TForm1.SelectBtnClick(Sender: TObject);
const
k180 = 180;
var
ch: integer;
begin
// 楕円１のデーター
val(radius_a1_Edit.Text, ar1, ch);
if ch <> 0 then begin
application.MessageBox('楕円１の半径a１数値ではありません。', '楕円１の半径a１', 0);
exit;
end;
if ar1 <= 0 then begin
application.MessageBox('楕円１の半径a１がゼロ 又はゼロ以下です。', '楕円１の半径a１', 0);
exit;
end;
val(radius_b1_Edit.Text, br1, ch);
if ch <> 0 then begin
application.MessageBox('楕円１の半径b１数値ではありません。', '楕円１の半径b１', 0);
exit;
end;
if br1 <= 0 then begin
application.MessageBox('楕円１の半径b１がゼロ 又はゼロ以下です。', '楕円１の半径b１', 0);
exit;
end;
val(Center_x1_Edit.Text, xo1, ch);
if ch <> 0 then begin
application.MessageBox('楕円１の中心位置x１数値ではありません。', '楕円１の中心位置x１', 0);
exit;
end;
val(Center_y1_Edit.Text, yo1, ch);
if ch <> 0 then begin
application.MessageBox('楕円１の中心位置y１数値ではありません。', '楕円１の中心位置y１', 0);
exit;
end;
val(angle_q1_Edit.Text, q1, ch);
if ch <> 0 then begin
application.MessageBox('楕円１の角度θ１数値ではありません。', '楕円１の角度θ１', 0);
exit;
end;
// 楕円２のデーター
val(radius_a2_Edit.Text, ar2, ch);
if ch <> 0 then begin
application.MessageBox('楕円２の半径a２数値ではありません。', '楕円２の半径a２', 0);
exit;
end;
if ar2 <= 0 then begin
application.MessageBox('楕円２の半径a２がゼロ 又はゼロ以下です。', '楕円２の半径a２', 0);
exit;
end;
val(radius_b2_Edit.Text, br2, ch);
if ch <> 0 then begin
application.MessageBox('楕円２の半径b２数値ではありません。', '楕円２の半径b２', 0);
exit;
end;
val(Center_x2_Edit.Text, xo2, ch);
if br2 <= 0 then begin
application.MessageBox('楕円２の半径b２がゼロ 又はゼロ以下です。', '楕円２の半径b２', 0);
exit;
end;
if ch <> 0 then begin
application.MessageBox('楕円２の中心位置x２数値ではありません。', '楕円２の中心位置x２', 0);
exit;
end;
val(Center_y2_Edit.Text, yo2, ch);
if ch <> 0 then begin
application.MessageBox('楕円２の中心位置y２数値ではありません。', '楕円２の中心位置y２', 0);
exit;
end;
val(angle_q2_Edit.Text, q2, ch);
if ch <> 0 then begin
application.MessageBox('楕円２の角度θ２数値ではありません。', '楕円２の角度θ２', 0);
exit;
end;
// 楕円の角度は、一回転180°なので、180°以下にします
repeat
if q1 >= k180 then q1 := q1 - k180;
if q1 < 0 then q1 := q1 + k180;
until (q1 < k180) and (q1 >= 0);
repeat
if q2 >= k180 then q2 := q2 - k180;
if q2 < 0 then q2 := q2 + k180;
until (q2 < k180) and (q2 >= 0);
inputdata_drawing;
// 交点が正しく計算できなかったらエラー表示
if cross_calc then begin
image1.Canvas.TextOut(20, 530,'交点を正しく計算できませんでした。');
end;
TandrwF := $04;
StartPosBtn.Enabled := true;
EndPosBtn.Enabled := true;
CalcBtn.Enabled := False;
end;
//----------------------------楕円の接線計算------------------------------
// a, b 半径
// q 角度
// xo, yo 楕円中心座標
// x, y 接線楕円外始点
// xt, yt 接線位置
//------------------------------------------------------------------------
function Tangent_Calc(a, b, q, xo, yo, x, y: double; var xt, yt: double): boolean;
var
r, qo, qs: double;
xs, ys: double; // 始点座標
xp, yp: double;
Dl, Al: double;
xa1, xa2, ya1, ya2: double;
x1, x2, y1, y2 : double;
begin
// 楕円の位置を原点に角度を０に座標変換
// 楕円中心から始点までの距離
r := sqrt((x - xo) * (x - xo) + (y - yo) * (y - yo));
// 始点の角度
qo := arctan2(y - yo, x- xo);
// 座標変換
qs := qo - q; // 楕円の角度分戻し
xp := cos(qs) * r; // 接線始点の位置x
yp := sin(qs) * r; // 接線始点の位置y
// 現在の接線位置座標変換
r := sqrt((xt - xo) * (xt - xo) + (yt - yo) * (yt - yo));
// 現在の接線位置の角度
qo := arctan2(yt - yo, xt- xo);
// 座標変換
qs := qo - q;
xt := cos(qs) * r; // 現在の接点位置X
yt := sin(qs) * r; // 現在の接点位置y
// 始点位置円座標に変換
ys := yp * a / b;
xs := xp;
// 円との接点計算
// 始点の座標が円内にある場合計算不可
Dl := xs * xs + ys * ys - a * a;
if Dl <= 0 then begin
result := False;
exit;
end;
result := true;
Dl := sqrt(Dl);
Al := xs * xs + ys * ys;
// 円上の座標
xa1 := a * (xs * a + ys * Dl) / Al;
xa2 := a * (xs * a - ys * Dl) / Al;
ya1 := a * (ys * a - xs * Dl) / Al;
ya2 := a * (ys * a + xs * Dl) / Al;
// 楕円の座標に変換
x1 := xa1;
x2 := xa2;
y1 := ya1 * b / a;
y2 := ya2 * b / a;
// 指定点と近いほうの接点選択
Al := sqrt((x1 - xt) * (x1 - xt) + (y1 - yt) * (y1 - yt));
Dl := sqrt((x2 - xt) * (x2 - xt) + (y2 - yt) * (y2 - yt));
if Al < Dl then begin
xt := x1;
yt := y1;
end
else begin
xt := x2;
yt := y2;
end;
// 元の座標系に変換
r := sqrt(xt * xt + yt * yt);
qo := arctan2(yt, xt);
qs := qo + q;
xt := cos(qs) * r + xo;
yt := sin(qs) * r + yo;
end;
// マウスで指定された位置を楕円上の位置に変換
procedure TForm1.Position_Calc;
var
q11, q12, qep: double;
qx, qy: double;
Dis0 : double;
// Dis1 : double;
begin
inputdata_drawing;
cross_calc;
// 楕円1の座標計算
if TanmodF = 1 then begin
qep := q1 / 180 * pi; // 楕円の角度
q11 := arctan2(posYs - yo1, posXs - xo1); // マウス指定点の楕円中心に対する角度
q12 := q11 - qep; // 楕円に対するマウス指定点の角度
if q12 >= 2 * Pi then q12 := q12 - 2 * pi;
if q12 < 0 then q12 := q12 + 2 * pi;
// 楕円上の座標計算 X座標
if (abs(q12 - pi / 2) < 1E-7) or (abs(q12 - pi / 2 - pi) < 1E-7) then qx := 0
else
qx := 1 / sqrt((1 / ar1) * (1 / ar1) + (tan(q12) / br1) * (tan(q12) / br1));
if cos(q12) < 0 then qx := - qx;
// 楕円上の座標計算 Y座標
qy := qx * tan(q12);
Dis0 := sqrt(qx * qx + qy * qy); // 楕円中心からの距離
{
qx := cos(q11) * Dis0 + xo1 - posXs;
qy := sin(q11) * Dis0 + yo1 - posYs;
Dis1 := sqrt(qx * qx + qy * qy);
image1.Canvas.TextOut(20,02, floatTostr(Dis1));
}
posYs := sin(q11) * Dis0 + yo1; // 全体Y座標
posXs := cos(q11) * Dis0 + xo1; // 全体X座標
end;
// 楕円2の座標計算
if TanmodF = 2 then begin
qep := q2 / 180 * pi; // 楕円の角度
q11 := arctan2(posYe - yo2, posXe - xo2); // マウス指定点の楕円中心に対する角度
q12 := q11 - qep; // 楕円に対するマウス指定点の角度
if q12 >= 2 * Pi then q12 := q12 - 2 * pi;
if q12 < 0 then q12 := q12 + 2 * pi;
// 楕円上の座標計算
if (abs(q12 - pi / 2) < 1E-7) or (abs(q12 - pi / 2 - pi) < 1E-7) then qx := 0
else
qx := 1 / sqrt((1 / ar2) * (1 / ar2) + (tan(q12) / br2) * (tan(q12) / br2));
if cos(q12) < 0 then qx := - qx;
// 楕円上の座標計算 Y座標
qy := qx * tan(q12);
Dis0 := sqrt(qx * qx + qy * qy); // 楕円中心からの距離
{
qx := cos(q11) * Dis0 + xo2 - posXe;
qy := sin(q11) * Dis0 + yo2 - posYe;
Dis1 := sqrt(qx * qx + qy * qy);
image1.Canvas.TextOut(20,02, floatTostr(Dis1));
}
posYe := sin(q11) * Dis0 + yo2; // 全体Y座標
posXe := cos(q11) * Dis0 + xo2; // 全体X座標
end;
TaninputDraw; // 接線指定点の表示
end;
// 接線指定点の表示
procedure TForm1.TaninputDraw;
begin
if TandrwF and 1 = 1 then begin
EllipseEx(image1.Canvas, image1.Height, 3, 2, clFuchsia, 5, 5,
(posXs - shift_x) * magnification + draw_margin, (posYs - shift_y) * magnification + draw_margin,
0, 0, 360);
end;
if TandrwF and 2 = 2 then begin
EllipseEx(image1.Canvas, image1.Height, 3, 2, clGreen, 5, 5,
(posXe - shift_x) * magnification + draw_margin, (posYe - shift_y) * magnification + draw_margin,
0, 0, 360);
end;
if TandrwF and 7 = 7 then CalcBtn.Enabled := true;
end;
// マウス割り込み
procedure TForm1.Image1MouseUp(Sender: TObject; Button: TMouseButton; Shift: TShiftState; X,
Y: Integer);
begin
if TandrwF and $04 = $00 then exit;
// 楕円1の処理
if TanmodF = 1 then begin
TandrwF := TandrwF or 1;
posXs := (X - draw_margin) / magnification + shift_x;
posYs := (Image1.Height - y - draw_margin) / magnification + shift_y;
end;
// 楕円2の処理
if TanmodF = 2 then begin
TandrwF := TandrwF or 2;
posXe := (X - draw_margin) / magnification + shift_x;
posYe := (Image1.Height - y - draw_margin) / magnification + shift_y;
end;
if (TanmodF = 2) or (TanmodF = 1) then Position_Calc;
end;
// 始点位置指定
procedure TForm1.StartPosBtnClick(Sender: TObject);
begin
TanmodF := 1;
end;
// 終点位置指定
procedure TForm1.EndPosBtnClick(Sender: TObject);
begin
TanmodF := 2;
end;
// 接線の計算
procedure TForm1.CalcBtnClick(Sender: TObject);
var
qo1, qo2 : double;
x1, y1, x2, y2: double;
xb1, yb1, xb2, yb2: double;
ckf: boolean;
posBXs : double; // 接線始点指定位置X
posBYs : double; // 接線始点指定位置y
posBXe : double; // 接線終点指定位置X
posBYe : double; // 接線終点指定位置y
begin
TanmodF := 0;
qo1 := q1 / 180 * pi;
qo2 := q2 / 180 * pi;
x1 := 0;
y1 := 0;
x2 := 0;
y2 := 0;
// 初期値バックアップ
posBXs := posXs;
posBYs := posYs;
posBXe := posXe;
posBYe := posYe;
// 接点の座標が変化しなくなるまで繰り返し計算
repeat
// 経過値バックアップ
xb1 := posXs;
yb1 := posYs;
xb2 := posXe;
yb2 := posYe;
// 楕円1の接線計算
ckf := Tangent_Calc(ar1, br1, qo1 , xo1, yo1, posXe, posYe, posXs, posYs);
if not ckf then break; // 接線が計算できなかったらブレーク
// 楕円2の接線計算
ckf := Tangent_Calc(ar2, br2, qo2 , xo2, yo2, posXs, posYs, posXe, posYe);
if not ckf then break; // 接線が計算できなかったらブレーク
// 直前の接線座標との差分計算
x1 := abs(xb1 - posXs);
y1 := abs(yb1 - posYs);
x2 := abs(xb2 - posXe);
y2 := abs(yb2 - posYe);
// 全ての差分がゼロになったら終了
until (x1 < 1E-13) and (y1 < 1E-13) and (x2 < 1E-13) and (y2 < 1E-13);
// 接線が計算出来なかったら
if not ckf then begin
application.MessageBox('接線指定点の位置が適正ではありません','注意',0);
CalcBtn.Enabled := False;
// 座標値バックアップから戻し
posXs := posBXs;
posYs := posBYs;
posXe := posBXe;
posYe := posBYe;
exit;
end;
// 表示用座標に変換
x1 := (posXs - shift_x) * magnification + draw_margin;
y1 := (posYs - shift_y) * magnification + draw_margin;
x2 := (posXe - shift_x) * magnification + draw_margin;
y2 := (posYe - shift_y) * magnification + draw_margin;
inputdata_drawing;
cross_calc;
TaninputDraw; // 接線指定点の表示
// 接線の作図
StraightLineDraw(image1.Canvas, image1.Height, 3, 1, clblack, x1, y1, x2, y2, False);
image2.Canvas.TextOut( 10, 380,'接線の始点と終点');
image2.Canvas.TextOut( 20, 395,'xps =' + floatTostrF(posXs,ffFixed,10,4));
image2.Canvas.TextOut(220, 395,'yps =' + floatTostrF(posYs,ffFixed,10,4));
image2.Canvas.TextOut( 20, 410,'xpe =' + floatTostrF(posXe,ffFixed,10,4));
image2.Canvas.TextOut(220, 410,'ype =' + floatTostrF(posYe,ffFixed,10,4));
end;
// 初期設定
procedure TForm1.FormCreate(Sender: TObject);
begin
top := (screen.Height - height) div 2;
left := (screen.Width - width) div 2;
// 線種配列确保
setlength(LPitch, LineN);
// 線種データーセット
LPitch[0].segment := 2; // 破線
LPitch[0].Pitch[0] := 6;
LPitch[0].Pitch[1] := 3;
LPitch[1].segment := 4; // １点鎖線
LPitch[1].Pitch[0] := 15;
LPitch[1].Pitch[1] := 3;
LPitch[1].Pitch[2] := 3;
LPitch[1].Pitch[3] := 3;
LPitch[2].segment := 6; // ２点鎖線
LPitch[2].Pitch[0] := 18;
LPitch[2].Pitch[1] := 3;
LPitch[2].Pitch[2] := 3;
LPitch[2].Pitch[3] := 3;
LPitch[2].Pitch[4] := 3;
LPitch[2].Pitch[5] := 3;
CalcBtn.Enabled := False;
StartPosBtn.Enabled := False;
EndPosBtn.Enabled := False;
// イメージクリア
imageClear;
image2.Canvas.Font.Name := 'ＭＳ ゴシック';
// image2.Canvas.Font.Style := [fsbold];
image2.Canvas.Font.Height := 13;
end;
end.
Ellipses_Tangent.zip
各種プログラム計算例に戻る