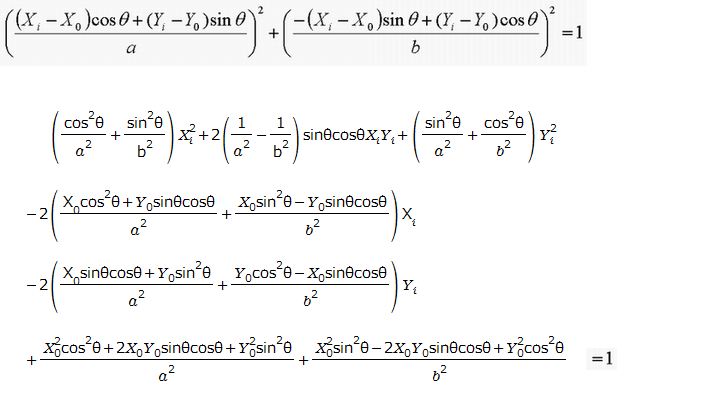
左図は、画像処理ソリューション(イメージングソリューション)に載っている、楕円式を二元二次方程式に変換する計算式です。
θは楕円の傾き角、Ｘo、Y oは、中心座標、Xi、Yi は、楕円上の座標です。
楕円と楕円の交点 その２
2019/01/15
Doubleで近似楕円で、僅かな中心位置のずれ、微小な角度差の時の桁落ち発生の値を少し改善しました。
楕円式での検算を追加し、1からのズレ量を判定し、ズレが大きい場合は、答えを出さない様にしました。
近似楕円で、微小なズレ、特に微小な角度のズレの時に1からのズレが大きくなります。
2019/01/09
Xの値を二つの楕円の式に入れて同じ値になるYの値を求める方法は、計算精度 extended 及び Extended で有効桁数不足が発生します。
計算方法を戻すことにし、軸対称については、同じXの値が出た時、計算軸角が大きくなる方向へ
移動する方法にしました。
2019/01/03
四次方程式の解法でデカルトの方法のプログラムにミスがあるのを修正しました。
フェラーリの方法は、不足していた二次での解法を追加しました。
方程式の解法結果のXの値からYの値を求める方法を二つの楕円の方程式から求めるように変更しました。
2018/10/27
extended演算側の自動演算の停止開始と交点無し停止判定の修正をしました。
(楕円弧の交点の時、交点が無くても停止しない場合がありました。)
2018/08/27
四次方程式の解法にフェラーリの方法を追加してみました。
実行画面のチェックボックスにチェックを入れるとフェラーリの方法で計算されます。
多倍長演算には追加していません。
2017/07/23
二つの楕円が同じ形状で、座標変換計算時、軸対称となる場合に四次方程式が正しく計算出来ないのを修正しました。
2016/06/24
楕円弧に対応しました、楕円弧の無い部分は交点を表示しません。
四次式の解法の計算にミスがあったので修正しました。
楕円の同士の交点を求める方法として、その１に、楕円上の点の距離を計算して交点を求める方法を記載しましたが、此処では四次方程式を解法する方法を取り上げます。
楕円の方程式は、二元二次方程式で、連立方程式は、四次方程式となります。
二つの楕円が接線となる場合、接点の位置の誤差が大きくなります。
条件によっては、桁落ちにより、交点が求められない場合も発生します、接点の位置の精度が必要な場合は、多倍長演算のプログラムを使用して下さい。
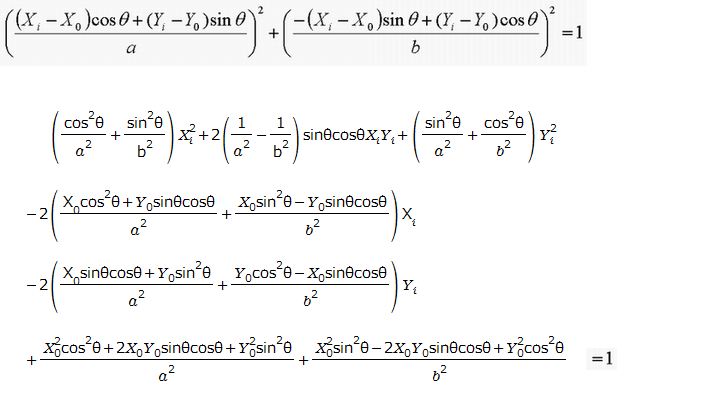
左図は、画像処理ソリューション(イメージングソリューション)に載っている、楕円式を二元二次方程式に変換する計算式です。
θは楕円の傾き角、Ｘo、Y oは、中心座標、Xi、Yi は、楕円上の座標です。
上記の方程式から、楕円の二元二次方程式を計算したら、二つの楕円の連立方程式を作成します。
連立方程式は、y の２乗の項を消去し、y= の式を導き出した、どちらかの楕円の二元二次方程式に代入することにより導き出します。
左図の例では、楕円１には、楕円２のC２を掛け、楕円２には、楕円１のC1 を掛ける様になっていますが、プログラムでは、楕円１は自分のC1で除算し、楕円２はC２で除算しています。
それは、出来る限り計算の桁落ちを防ぐ方法として使用しています。
これで、四次方程式が出来たので、次は四次方程式の解法です。
Delphiに複素数があるので、複素数を使用してプログラムを組めば良いのかもしれませんが、計算の便宜上、複素数を使用しない方法にしました。
自分で、四次方程式の解法プログラムを一から組むのは、能力不足なので、デカルトの方法の資料をインターネットで探し、Ｄｅｌｐｈｉ用にプログラムを組みました。
プログラムが正しいかどうかは、高精度計算サイトの結果と比較して検証をしました。
フェラーリの方法については、インターネットで見つけた、C言語で書かれたものを、単純にDelphi用に変換しました。
実際にプログラムを組み、テストをするとすぐに分かるのですが、四次方程式だけでは、解法できない楕円の組み合わせが有ることが、直ぐにわかります。
最初のプログラムを完成させる迄は、全てのパターンについて、解法できるものと思っていましたが、直ぐに裏切られました。
縦横比の等しい楕円で、傾きが同じだと、四次方程式の連立方程式にならず、二次方程式の連立方程式になります。
円の交点と同じです、縦横比と傾き角が同じ場合、円を傾けた時(Ｚ軸上から斜めに見ると、楕円に見える)と同じなので、円と同じように二次方程式になるようです。
四次方程式の最初のＡの項が０、或いは０と見なせるぐらい小さい場合は、二次方程式で解けば、近似解が得られますが、Ａの項がどれ位の値まで小さくなったら、二次方程式を使うかの判別の設定が難しいです。
Ａの項が０でない限り四次方程式を解けば良いと思われるかもしれませんが、演算上の桁落ちで計算結果が大きくずれてしまいます。
二次式で計算する場合も、Ｃの最小値を限定しないと桁落ちで計算結果が大きくずれることが発生します。
演算上の有効桁数が１５桁でも上から１３桁まで等しい値の差分をとると有効桁数は２桁になってしまいます、これが桁落ちの大きな要因の様です。
四次方程式の解法プログラムの修正により、計算軸角に対して対称の関係が発生しても、演算エラーは出なくなりましたが、Yの値を求めるときの計算は、計算軸角に対する対称の関係からずらす必要があります。
上記計算式の Y=
の式にXの値を入れて計算すると、Xの値が同じで、Yの値が違う計算は不可能ですので、計算軸角を変更して同じXの値に成らないようにします。
方程式が 解けた場合、二つ、又は四つの値で、同じXの値が発生した場合、計算軸角に１°加算し再計算して、同じXの値が出るか確認します。
同じXの値がなくなれば、Yの値の計算へ進みますが、無くならない場合は、三回繰り返して、三度同じXの値が出た場合は、接点と判定します。
計算軸角に対して、二つの楕円が対称となる場合、必ず同じXの値が出るので、このXの値の発生を調べて、計算軸角の変更をするので、問題なく対称から外す事が出来ます。
又、軸対称とは関係なく、同じXの値が出る場合がありますので、同じXの値の発生をチェックして、計算軸角の変更をすると、問題なくYの値を求めることができます。
以前は、計算軸対称となる角度を避けて計算していましたが、計算軸対称とは関係なく同じXの値が発生するのを見逃していました。
二つの楕円の方程式にXの値をいれて、同じYの値が出るのを確認するプログラムを作成してみましたが、多倍長演算では、問題なく計算出来ましたが、Double、Extendedの精度では桁落ちで、安定してYの値を求めることとが出来ませんでした。
同じXの値が出なければ、計算軸角をゼロ度から変更しなくても、計算は可能なのですが、３０°に変更した方が、二つの楕円の軸角の差が小さいときに安定して結果を出すことが出来ます。
此処でのプログラムでは、楕円比の大きい方の軸角が ３０°の角度になるように座標変換をして計算をしています。
片方が円の場合は、円でない方の楕円の計算軸角を３０°に座標変換します。
以上の対策により、円同士の交点、楕円比が同じで、角度が同じ以外は、四次方程式で計算され、円同士の交点、楕円比が同じで、角度が同じ場合は、二次方程式で計算され、計算出来ないパターンがなくなります。
しかし、円と楕円の境界を何処にするかの問題は残ります。
計算の精度が高く有効桁数が多ければ、僅かな半径の差でも、楕円としての計算が出来ます。
二つの楕円の或いは円、円と楕円の二元二次方程式から連立方程式を作成した時、Ａ、B の項が０、或いは０に近ければ二次方程式になりますが、二次方程式の解法は、ごく一般的に知られた方法を使用します。
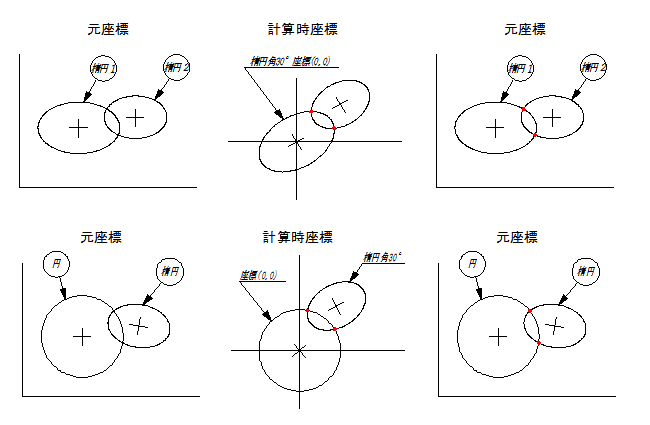楕円の角度が３０°になるように座標変換をして交点を計算、その後、元の座標に戻します。
縦横比の大きい方の楕円の角度が３０°になるようにすると、円がある場合は、円ではない方の楕円の角度が３０°になります。
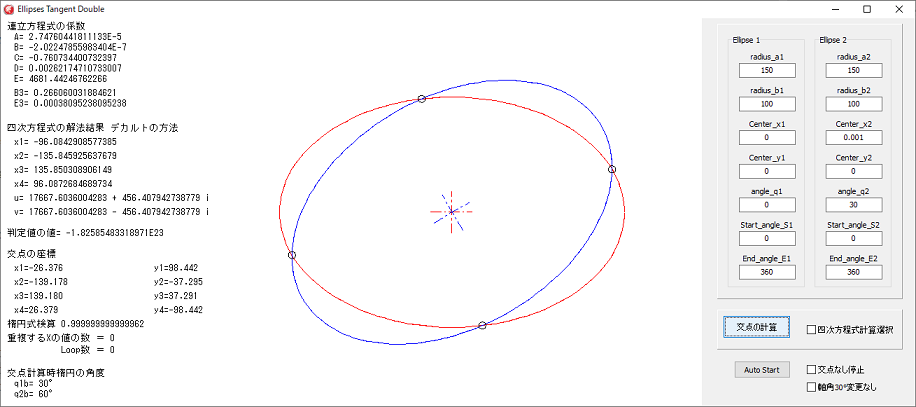左図は、プログラムの実行例です。
A=～E=は、四次方程式の各項の値です。
X1～X4=は、四次方程式を解法した結果です。
カルダノ解法の場合、結果の値の最後に"i"の符号が付いた場合は、虚数となり、実数解ではありませんので、その座標には交点が存在しないことになります。
フェラーリ解法の場合は、虚数"i"の値が０(ゼロ)でない場合、実数解ではありません。
u=,v=は、単に途中での計算結果を表しています。交点とは関係ありません。
二次方程式で解法した場合は、X1=,X2=の２つの答えしか表示されません。
四次方程式計算選択のチェックボックスにチェックを入れるとフェラーリの方法で計算されます。
計算時軸角を30°に変更しないで計算出来るモードもありますが、デバッグ用で、計算軸角を変更したほうが計算精度が上がります。
軸対称の問題
デカルトの解法プログラム修正により、軸対称時でも、問題なく方程式の解法が出来るようになりましたが、Y=の式を利用する為に同じXの値が発生した場合は、計算軸角を変更しています。
フェラーリの解法にも、軸対称の対策を入れました。
計算は出来る様になりましたが、近似する楕円で楕円の中心が水平方向だけ少しズレ、更に、軸角がゼロ近辺で、二つの楕円角が近似する場合、桁落ちの影響が大きくなり、計算出来ない場合があります。
計算軸角を変更すれば問題なく計算が出来るので、計算軸角の変更はそのまま残してあります。
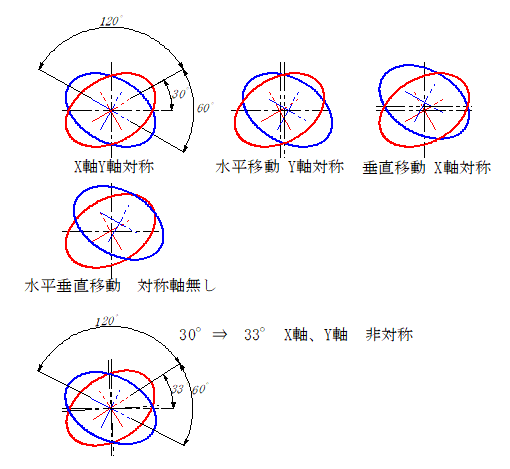
片方の楕円の角度を３０°にしている場合、楕円の角度の差が６０°、１２０°の時、水平軸、又は垂直軸に対して軸対称になります。
この軸対称は、二つの楕円が同じ値で、同心、片方の楕円に対して、もう一方の楕円を水平移動 又は 垂直移動した場合に軸対称が発生します。
水平垂直両方へ移動した場合は、軸対称は発生しません。
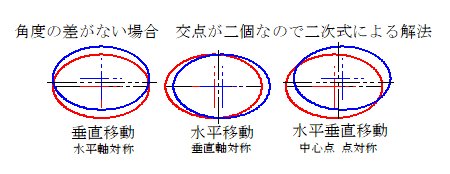
参考
二つの楕円が座標以外等しい場合は、二次方程式の解法となります。
プログラム
プログラムには、楕円の交点その1と同じように、Delphiの標準作図ルーチンでなく、専用のルーチンを使用して作図しています。
方程式の解法時、演算精度が、doubleでは不足するので、Extendedにしてあります。
作図の部分は、doubleでも問題ありません。
64ビットでコンパイルすると、doubleの精度になってしまい注意が必要です。
doubleの場合、接線、或いは接線に近い場所が検出できない場合があります。
(注)
プログラムの中には、四次方程式で計算するか、二次方程式で計算するか、実交点があるかどうか等の為の判定の固定値が設定してあります。
判定すべき値が楕円の大きさによってあまり変動しない様に、一番大きい楕円の半径が一定の値になる様に変換して計算しています。
計算の誤差もあるので、誤差の値の一定化の為にも、計算時の半径の値が一定になる様にするのは有効な手段です。
多倍長演算
計算精度に double
を使用すると、計算結果として 有効桁数７桁程度しか得ることが出来ません。
doubleの計算そのものには、15桁ほどあるのですが、計算途中の桁落ち影響で有効桁数が下がります。
場合によっては、桁落ちにより、方程式の解法が出来ない場合があります。
Extendedは x64
ではフォローしていませんので、高い精度を必用とする場合は多倍長演算を使用する必要があります。
そこで、多倍長演算の
MPArith
を使用したプログラムを作成しました。
多倍長演算ならば、計算結果として有効桁数２０桁以上の精度を得ることが出来ます。
多倍長演算は、楕円の交点を求める計算部分だけで、作図部分は不要なので使用していません。
MPArithからmparith_2017-08-03.zipをダウンロードします。
ファイルの日付が変わるので、変わっていたら新しいのをダウンロードして下さい。
Zipファイルを解凍して、解凍したフォルダーにパス(ツール->オプション->Delphiオプション->ライブラリ->ライブラリパス)を追加し、Uses に mp_types, mp_realを追加すれば使用可能になります。
一般の四則演算(=+-*/)は使用できず全て専用のルーチンとなるのでプログラムが長くなります。
使用方法は、ホームページ及び、ｈｌｐファイルを見れば分かりますが、ｈｌｐファイルは古いタイプなので、Win10で見るためには、変換をするか、WinHlp32.exeを入れ替える必要があります。
此処でダウンロードして、解凍した EllipsesNodeCX フォルダーの中のものが、多倍長演算にしたものです。
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.ExtCtrls, Vcl.StdCtrls, Vcl.Buttons, math;
type
TELLIPSE = record
fRad_X : extended; // X 方向半径
fRad_Y : extended; // Y 方向半径
fAngle : extended; // 楕円角度
fCx : extended; // 楕円中心位置 X
fCy : extended; // 楕円中心位置 Y
startAngle : extended; // 開始角
endAngle : extended; // 終了角
end;
TForm1 = class(TForm)
Panel1: TPanel;
Ellipse1Box: TGroupBox;
radius_a1_Edit: TLabeledEdit;
radius_b1_Edit: TLabeledEdit;
Center_x1_Edit: TLabeledEdit;
Center_y1_Edit: TLabeledEdit;
angle_q1_Edit: TLabeledEdit;
Ellipse2Box: TGroupBox;
radius_a2_Edit: TLabeledEdit;
radius_b2_Edit: TLabeledEdit;
Center_x2_Edit: TLabeledEdit;
Center_y2_Edit: TLabeledEdit;
angle_q2_Edit: TLabeledEdit;
Panel2: TPanel;
SelectBtn: TBitBtn;
Image1: TImage;
Image2: TImage;
End_angle_E2: TLabeledEdit;
Start_angle_S2: TLabeledEdit;
End_angle_E1: TLabeledEdit;
Start_angle_S1: TLabeledEdit;
Timer1: TTimer;
Button1: TButton;
CheckBox1: TCheckBox;
CheckBox2: TCheckBox;
CheckBox3: TCheckBox;
procedure FormCreate(Sender: TObject);
procedure SelectBtnClick(Sender: TObject);
procedure Button1Click(Sender: TObject);
procedure Timer1Timer(Sender: TObject);
private
{ Private 宣言 }
procedure imageClear(i: integer);
function Dist(x1, y1, x2, y2 : extended): extended;
function Angle(dx, dy: extended): extended;
procedure LineSub(Tcv: TCanvas; px1, py1, px2, py2: extended);
procedure pitchControl(NLine, LW: integer);
procedure LineSubPitch(Tcv : TCanvas; Ln: integer; var i: integer; var d1: extended; px1, py1, px2, py2:extended);
function angleSe(a, b, rad: extended): extended;
procedure EllipseEx(Tcv: TCanvas; h, lf, lw: integer; lc: Tcolor; a, b, x, y, rq, sq, eq: extended);
procedure quadratic_transform(a, b, x, y, qdeg: extended; var A0, B0, C0, D0, E0, F0: extended);
procedure inputdata_drawing;
function cross_calc: boolean;
function cross_quadratic(a, b, c, d, e: extended; var x1, x2, x3, x4: extended): byte;
procedure trance(Xn, Yn, defQ, xo1, yo1: extended; var x, y: extended);
procedure StraightLineDraw(Tcv: TCanvas; h, lf, lw: integer; lc: Tcolor; xs, ys, xe, ye: extended; sf: boolean);
function angle_amendment(angle : extended): extended;
function intersection_judge(Ellipse1, Ellipse2: TEllipse; X, Y: extended): boolean;
function cube_root(x: extended): extended;
function cubic_equation(a2, a1, a0: extended; var solution: array of extended): integer;
function quartic_equation(a3, a2, a1, a0: extended; var solution4: array of extended): integer;
function Newcross_quadratic(a, b, c, d, e: extended; var x1, x2, x3, x4: extended): byte;
function quadratic_equation(a, b, c: extended; var x1, x2: extended; frg: boolean): byte;
function Ellipse_judge(Ellipse: TEllipse; x, y: extended): boolean;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
const
PitchN = 5; // 線ピッチ設定数
LineN = 3; // 線種数
LIMIT8 = 0.00000001;
type
TLinePitch = Record // 線種用レコード
Pitch : array[0..PitchN] of extended; // ピッチ 線長さ 空白の繰り返し
segment : integer; // ピッチ数
End;
var
LPitch : array of TLinePitch; // 線種用 (線ピッチ)
VPitch : array[0..PitchN] of extended; // 線幅による線ピッチ設定用
magnification : extended;
Ellipse1 : TELLIPSE; // 楕円１
Ellipse2 : TELLIPSE; // 楕円２
shift_x : extended;
shift_y : extended;
d01 : extended;
d0p : integer;
scale : extended;
timeF : boolean;
EllipCheck : extended;
const
draw_margin = 30; // 左右上下作図マージン
procedure TForm1.imageClear(i: integer);
begin
image2.Canvas.Brush.Style := bsSolid;
image2.Canvas.Brush.Color := clWhite;
image2.Canvas.FillRect(Rect(0, 0, image2.Width, image2.Height));
if i = 1 then exit;
image1.Canvas.Brush.Style := bsSolid;
image1.Canvas.Brush.Color := clWhite;
image1.Canvas.FillRect(Rect(0, 0, image1.Width, image1.Height));
end;
//-----------------------------------------------
// 線幅によるピッチの補正
// 線幅を広くするとスペースが狭くなるので広げます
// NLine 線種
// LW 線幅
//-----------------------------------------------
procedure TForm1.pitchControl(NLine, LW: integer);
var
i : integer;
begin
// 線幅によるピッチの補正
for i := 0 to pitchN do begin
if i mod 2 <> 0 then // 奇数配列noセグメントがスペース
Vpitch[i] := LPitch[NLine].Pitch[i] + LW // スペースに線幅加算
else
Vpitch[i] := LPitch[NLine].Pitch[i];
end;
end;
//----------------------------
// 作図用 二点間線引き
//----------------------------
procedure TForm1.LineSub(Tcv: TCanvas; px1, py1, px2, py2: extended);
var
x1, y1, x2, y2 : integer ;
begin
x1 := Round(px1);
y1 := Round(py1);
x2 := Round(px2);
y2 := Round(py2);
Tcv.MoveTo(x1, y1);
Tcv.LineTo(x2, y2);
end;
//----------------------
// 距離（長さ）を計算
// x1, y1 : 始点
// x2, y2 : 終点
// out : 距離(長さ)
//----------------------
function TForm1.Dist(x1, y1, x2, y2 : extended): extended;
begin
Result := Sqrt((x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1)) ;
end;
//--------------------------------
// 角度を計算[rad]
// dx : X方向差分
// dy : Y方向差分
// out: 角度 (0～2 * Pi)
//--------------------------------
function TForm1.Angle(dx, dy: extended): extended ;
var
r : extended ;
begin
Result := 0.0;
if (Abs(dx) < LIMIT8) and (Abs(dy) < LIMIT8) then exit;
r := ArcTan2(dy, dx);
if r < 0.0 then r := r + 2.0 * Pi;
Result := r;
end;
//--------------------------------------
// 線分の表示・サブ２：線種指定
// Ln : 線種番号(1-)
// i : 開始セグメント番号(終了時更新)
// d1 : 開始ピッチ長さ (終了時更新)
// px1, py1 : 線分始点[mm]
// px2, py2 : 線分終点[mm]
//--------------------------------------
procedure TForm1.LineSubPitch(Tcv: TCanvas; Ln: integer; var i: integer; var d1: extended; px1, py1, px2, py2:extended);
var
x1, y1, x2, y2 : extended;
a, sa, ca, d, p : extended;
PenStyle : TPenstyle;
begin
PenStyle := Tcv.Pen.Style; // 線種バックアップ
Tcv.Pen.Style := psSolid;
if (Ln < 0) or (Ln >= LineN) then begin // 無い線種は実線
LineSub(Tcv, px1, py1, px2, py2);
Tcv.Pen.Style := PenStyle; // 線種戻し
exit;
end;
a := Angle(px2 - px1, py2 - py1); // 角度計算
d := Dist(px1, py1, px2, py2); // 距離計算
ca:= Cos(a); // コサイン
sa:= Sin(a); // サイン
x1:= px1; // 始点x
y1:= py1; // 始点y
repeat
p := Vpitch[i] - d1; // ピッチと開始ピッチ長さ差分 残り分
if (p > d) then p := d; // 距離より残り分が大きい場合 距離
x2 := x1 + p * ca ; // 新しい位置計算
y2 := y1 + p * sa ;
if (i mod 2) = 0 then // セグメント偶数毎に線引き 空白部線引きしない
LineSub(Tcv, x1, y1, x2, y2);
x1 := x2; // 終点を始点にセット
y1 := y2;
d := d - p ; // 残り長さ計算
if d > LIMIT8 then begin // 残り長さがあったら
d1 := 0.0; // 開始ピッチ長さクリア
Inc(i); // セグメントカウンターインクリメント
if i >= LPitch[Ln].segment then i := 0; // セグメント数を超えたらゼロに戻し
end;
until d <= LIMIT8;
d1 := d1 + p; // 開始ピッチ長さ
Tcv.Pen.Style := PenStyle; // 線種戻し
end;
//------------------------------------------
// 楕円の開始角を 基礎円の開始角に変換
//------------------------------------------
function TForm1.angleSe(a, b, rad: extended): extended;
const
KMIN = 0.00000001;
var
l : extended;
begin
// 90°, 270°, 0°, 180° 360°近傍は計算しない
if (abs(rad - pi / 2) < KMIN) or (abs(rad - pi - pi / 2) < KMIN)
or (abs(rad) < KMIN) or (abs(rad - pi) < KMIN) or
(abs(rad - pi * 2) < KMIN)
then begin
result := rad;
exit;
end;
// 底辺の長さ計算 ( b / a の値がいつも正の値なので元の角度によって角度を補正)
// 分母がゼロに近くなる時もあるので、判別が不要なarctan2を使用します
l := b / a / tan(rad);
// 180°以下だったら
if rad < pi then
result := arctan2(1, l)
else
// 360°以下だったら
if rad < pi * 2 then
result := arctan2(1, l) + pi
// 360°を超えていたら
else
result := arctan2(1, l) + pi * 2;
end;
//-------------------------------------------------------------
// 直線の描画
// 直線の開始はsfをTrueにします。
// つながった直線、折れ線を描画する場合は、sfをFalseに
//-------------------------------------------------------------
procedure TForm1.StraightLineDraw(Tcv: TCanvas; h, lf, lw: integer; lc: Tcolor; xs, ys, xe, ye: extended; sf: boolean);
begin
Tcv.Pen.Width := lw;
Tcv.Pen.Color := lc;
// 線幅によるピッチの補正
pitchControl(lf, lw);
// y方向変換
ys := h - ys;
ye := h - ye;
if sf then begin
d01 := 0;
d0p := 0;
end;
LineSubPitch( // ピッチ線描画
tcv, // TCanvas
lf, // 線種
d0p, // セグメント位置
d01, // 長さ
xs, // 始点X
ys, // 始点Y
xe, // 終点X
ye // 終点Y
);
end;
//---------------------------------------
// 楕円の描画
// Windows為ののy方向変換は,このルーチンで行います。
// tcv 描画キャンバスの指定
// h キャンバスの高さ
// lf 線の種類
// lw 線の幅
// lc 線の色
// a 半径a
// b 半径b
// x 中心位置 x
// y 中心位置 y
// rq 楕円の角度
// sq 描画開始角
// eq 描画終了
//---------------------------------------
procedure TForm1.EllipseEx(Tcv : TCanvas; h, lf, lw: integer; lc: Tcolor; a, b, x, y, rq, sq, eq: extended);
var
sqrad, eqrad : extended;
qrad : extended;
Ssqrad, Seqrad : extended;
sp : integer;
dq : extended;
d1 : extended;
dp : integer;
xf, yf : extended;
rdist, nrad : extended;
px1, py1 : extended;
px2, py2 : extended;
i : integer;
begin
Tcv.Pen.Width := lw;
Tcv.Pen.Color := lc;
// y方向変換
y := h - y;
// 線幅によるピッチの補正
pitchControl(lf, lw);
// 終了角と開始角が一致したら全周
if abs(sq - eq) < LIMIT8 then begin
sq := 0;
eq := 360;
end;
// 分割数 半径に応じて調整
sp := round(sqrt(a + b) * 4); // 分割数
// 楕円の計算と描画
sqrad := sq / 180 * pi;
eqrad := eq / 180 * pi;
qrad := pi / 180 * rq; // 回転角 ラジアン
Ssqrad := angleSe(a, b, sqrad); // 基本円角度に変換
Seqrad := angleSe(a, b, eqrad); // 基本円角度に変換
// 分割微小角計算 分割数角度で補正
if Seqrad >= Ssqrad then begin
sp := round(sp * (Seqrad - Ssqrad) / pi);
if sp = 0 then sp := 1;
dq := (Seqrad - Ssqrad) / sp; // 分割微小角 ラジアン
end
else begin
sp := round(sp * (Pi * 2 - Ssqrad + Seqrad) / pi);
if sp = 0 then sp := 1;
dq := (Pi * 2 - Ssqrad + Seqrad) / sp; // 分割微小角 ラジアン
end;
// 開始点の計算
d1 := 0; // 長さ
dp := 0; // セグメント位置
xf := cos(Ssqrad) * a; // 基本楕円座標X スタート座標
yf := sin(Ssqrad) * b; // 基本楕円座標y スタート座標
nrad := arctan2(yf, xf) + qrad; // 新しい角度 回転角加算
rdist := sqrt(xf * xf + yf * yf); // 中心と楕円座標の距離
px1 := cos(nrad) * rdist + x; // 開始座標X
py1 := sin(nrad) * -rdist + y; // 開始座標Y -rdistはY座標反転の為
// WindowはY座標方向が逆のため
// 分割数分計算繰り返し描画
for i := 1 to sp do begin
xf := cos(Ssqrad + dq * i) * a;
yf := sin(Ssqrad + dq * i) * b;
nrad := arctan2(yf , xf) + qrad;
rdist := sqrt(xf * xf + yf * yf);
px2 := round(cos(nrad) * rdist + x); // 終点座標X
py2 := round(sin(nrad) * -rdist + y); // 終点座標Y
// ピッチ線描画
LineSubPitch( // ピッチ線描画
tcv, // TCanvas
lf, // 線種
dp, // セグメント位置
d1, // 長さ
px1, // 始点X
py1, // 始点Y
px2, // 終点X
py2 // 終点Y
);
px1 := px2; // 終点Xを始点Xに
py1 := py2; // 終点Yを始点Yに
end;
end;
//-------------------------------------------------
// 楕円の方程式 二次方程式への変換
// AX^2 + BXY + CY^2 + DX + EY + F の A,B,C,D,E,F
//-------------------------------------------------
procedure TForm1.quadratic_transform(a, b, x, y, qdeg: extended; var A0, B0, C0, D0, E0, F0: extended);
var
Q : extended;
sin_Q, cos_q : extended;
ah2, bh2 : extended;
sinh2, cosh2 : extended;
sincosQ : extended;
xh2, yh2, xy : extended;
begin
Q := qdeg / 180 * pi; // ラジアン単位に変換
sin_Q := sin(Q);
cos_Q := cos(Q);
ah2 := a * a;
bh2 := b * b;
sinh2 := sin_Q * sin_Q;
cosH2 := cos_Q * cos_Q;
sincosQ := sin_Q * cos_Q;
xh2 := x * x;
yh2 := y * y;
xy := x * y;
A0 := cosh2 / ah2 + sinh2 / bh2;
B0 := 2 * (1 / ah2 - 1 / bh2) * sincosQ;
C0 := sinh2 / ah2 + cosh2 / bh2;
D0 := -2 * ((x * cosh2 + y * sincosQ) / ah2 + (x * sinh2 - y * sincosQ) / bh2);
E0 := -2 * ((x * sincosQ + y * sinh2) / ah2 + (y * cosh2 - x * sincosQ) / bh2);
F0 := (xh2 * cosh2 + 2 * xy * sincosQ + yh2 * sinh2) / ah2
+ (xh2 * sinh2 - 2 * xy * sincosQ + yh2 * cosh2) / bh2
- 1;
end;
//---------
// 立方根
//---------
function TForm1.cube_root(x: extended): extended;
var
z : extended;
begin
z := power(abs(x), 1 / 3);
if x < 0 then z := -z;
result := z;
end;
//------------------
// 二次方程式の解法
//------------------
function TForm1.quadratic_equation(a, b, c: extended;var x1, x2: extended; frg: boolean): byte;
const
MINIMAM2F = 1E-6;
var
f : extended;
xim1, xim2, xim3: string;
V : integer;
begin
result := 0;
f := b * b - 4 * a * c;
if f < 0 then
if abs(f) < MINIMAM2F then f := 0; // 微小な複素数は許容
if f >= 0 then begin
X1 := (-b + sqrt(f)) / 2 / a;
X2 := (-b - sqrt(f)) / 2 / a;
result := 1 + 2;
end
else begin
x1 := -b / a / 2;
x2 := x1;
xim3 := floattostr(sqrt(abs(f)) / 2 / a) + ' i';
xim1 := '+ ' + xim3;
xim2 := '- ' + xim3;
end;
image2.Canvas.Brush.Style := bsSolid;
image2.Canvas.Brush.Color := clWhite;
if frg then begin
V := 270;
with image2.Canvas do begin
FillRect(Rect(0, 165 + V, 300, 165 + V + 45));
TextOut(10, 150 + V,'楕円上の値計算結果');
TextOut(20, 167 + V,'y1= ' + floattostr(x1) + ' ' + xim1);
TextOut(20, 184 + V,'y2= ' + floattostr(x2) + ' ' + xim2);
end;
end
else begin
with image2.Canvas do begin
TextOut(10, 150,'二次方程式の解法結果');
TextOut(20, 170,'x1= ' + floattostr(x1) + ' ' + xim1);
TextOut(20, 190,'x2= ' + floattostr(x2) + ' ' + xim2);
end;
end;
end;
//----------------------------------------
// 三次方程式の解法カルダノの方法
//----------------------------------------
function TForm1.cubic_equation(a2, a1, a0: extended;var solution: array of extended): integer;
var
i : integer;
x, y: extended;
p, q, theta: extended;
A, B, C, D, F, R, O, S, T: extended;
begin
p := 3 * a1 - a2 * a2;
q := 27 * a0 - 9 * a1 * a2 + 2 * a2 * a2 * a2;
D := q * q + 4 * p * p * p;
D := - D / (54 * 54);
q := q / 27;
A := -a2 / 3;
B := - q / 2;
C := sqrt(abs(D));
for i := 0 to 4 do solution[i] := 0;
if D = 0 then begin
if q = 0 then begin
for i := 0 to 2 do solution[i] := A;
end
else begin
F := cube_root(B);
solution[0] := A + 2 * F;
solution[2] := A - F;
solution[1] := solution[2];
end;
end
else
if D > 0 then begin
x := B * B + D;
y := power(x, 1 / 6);
theta := arctan2(C, B) / 3;
R := y * cos(theta);
O := y * sin(theta) * sqrt(3);
solution[0] := A + 2 * R;
solution[1] := A - R - O;
solution[2] := A - R + O;
end
else begin
S := cube_root(B + C);
T := cube_root(B - C);
solution[0] := A + S + T;
solution[2] := A - (S + T) / 2;
solution[1] := solution[2];
y := sqrt(3) / 2;
solution[3] := (S - T) * y;
solution[4] := - solution[3];
end;
result := 0;
end;
//---------------------------------------------
// 四次方程式の解法フェラーリの方法 ** a4 = 1
// a4x^4 + a3x^3 + a2x^2 + a1x + a0
//---------------------------------------------
function Tform1.quartic_equation(a3, a2, a1, a0: extended;var solution4: array of extended): integer;
const
IMAGIMIN = 1E-8; // double の有効桁数15桁位の限度 誤差 0.0001 程度
AMIN = 1E-5; // doubleのq=0時のaの許容値
var
b3, p, q, o: extended;
u, x, y, z: extended;
Dp, Dm, rtDp, rtDm, R, S, T: extended;
solution3: array[0..4] of extended;
a, b, c: extended;
begin
result := 0;
if (a3 = 0) and (a2 = 0) and (a1 = 0) then exit;
b3 := a3 / 4;
p := a2 - 6 * b3 * b3;
q := a1 - 2 * a2 * b3 + 8 * b3 * b3 * b3;
// 二つの楕円が同軸の時 q = 0
// x^4 + bx^2 + c = 0 の 解法
if q = 0 then begin
b := -1 / 2 * a2;
c := a0;
a := b * b - c;
if abs(a) < AMIN then a := 0; // 小さな虚数は許容
if a >= 0 then begin
a := sqrt(a);
solution4[0] := sqrt(b + a);
solution4[1] := sqrt(b - a);
solution4[2] := -sqrt(b - a);
solution4[3] := -sqrt(b + a);
solution4[4] := 0;
solution4[5] := 0;
solution4[6] := 0;
solution4[7] := 0;
end
else begin
a := sqrt(abs(a));
c := sqrt(a * a + b * b);
a := sqrt((c - b) / 2);
b := sqrt((c + b) / 2);
solution4[0] := b;
solution4[1] := -b;
solution4[2] := -b;
solution4[3] := b;
solution4[4] := a;
solution4[5] := a;
solution4[6] := -a;
solution4[7] := -a;
end;
image2.Canvas.TextOut(20, 250, 'ax^4 + bx^2 + cの解');
exit;
end;
o := a0 - a1 * b3 + a2 * b3 * b3 - 3 * power(b3, 4);
x := 2 * p;
y := p * p - 4 * o;
z := - q * q;
if cubic_equation(x, y, z, solution3) <> 0 then begin
result := 1;
exit;
end;
u := solution3[0];
image2.Canvas.TextOut(20, 250, '三次式の解 ' + floattostr(u));
if u <= 0 then exit;
R := -sqrt(u) / 2;
S := (p + u) / 2;
T := -q / (4 * R);
Dp := R * R - S + T;
Dm := R * R - S - T;
if abs(Dp) < IMAGIMIN then Dp := 0; // doubleで計算の誤差許容
if abs(Dm) < IMAGIMIN then Dm := 0;
rtDp := sqrt(abs(Dp));
rtDm := sqrt(abs(Dm));
if DP >=0 then begin
solution4[0] := - b3 + R - rtDp;
solution4[1] := - b3 + R + rtDp;
solution4[4] := 0;
solution4[5] := 0;
end
else begin
solution4[0] := - b3 + R;
solution4[1] := - b3 + R;
solution4[4] := - rtDp;
solution4[5] := rtDp;
end;
if DM >= 0 then begin
solution4[2] := - b3 - R - rtDm;
solution4[3] := - b3 - R + rtDm;
solution4[6] := 0;
solution4[7] := 0;
end
else begin
solution4[2] := - b3 - R;
solution4[3] := - b3 - R;
solution4[6] := - rtDm;
solution4[7] := rtDm;
end;
end;
//----------------------------------------------
// 二次方程式 四次方程式の解法(フェラーリの方法)
//----------------------------------------------
function TForm1.Newcross_quadratic(a, b, c, d, e: extended; var x1, x2, x3, x4: extended): byte;
const
MINIMAM4 = 1E-17;
IMAGIMIN = 1E-8;
MINIMAM2 = 1E-14;
// MINIMAM2F = 1E-12;
var
solution4: array[0..7] of extended;
i, j : integer;
Lng : integer;
strout : string;
begin
result := 0;
for i := 0 to 7 do solution4[i] := 0;
if (abs(a) > MINIMAM4) then begin
b := b / a;
C := c / a;
d := d / a;
e := e / a;
// 四次方程式の解法
i := quartic_equation(b, c, d, e, solution4);
if i <> 0 then exit;
image2.Canvas.TextOut(10, 150,'四次方程式の解法結果フェラーリの方法');
for i := 0 to 3 do begin
strout := floatTostr(solution4[i]);
lng := length(strout);
for j := 0 to 23 - lng do strout := strout + ' ';
strout := strout + floatTostr(solution4[i + 4]) + ' i';
image2.Canvas.TextOut(20, 170 + i * 20 ,'x' + inttostr(i + 1) + '= ' + strout);
end;
x1 := solution4[0];
x2 := solution4[1];
x3 := solution4[2];
x4 := solution4[3];
result := 0;
if abs(solution4[4]) < IMAGIMIN then result := result + 1;
if abs(solution4[5]) < IMAGIMIN then result := result + 2;
if abs(solution4[6]) < IMAGIMIN then result := result + 4;
if abs(solution4[7]) < IMAGIMIN then result := result + 8;
end;
if (abs(a) <= MINIMAM4) and (abs(c) > MINIMAM2) then begin
// 二次方程式の解法
result := quadratic_equation(c, d, e, x1, x2, False);
end;
end;
//-----------------------------------------------------
// 四次 二次方程式の解法 デカルトの方法
// ax^4 + bx^3 + cx^2 + dx + e = 0
// x の 値は 4個
// 虚数にならない X を フラグにして byteで返します
// x1 bit0 x2 bit1 x3 bit2 x4 bit3
//-----------------------------------------------------
function TForm1.cross_quadratic(a, b, c, d, e: extended; var x1, x2, x3, x4: extended): byte;
const
// MINIMAM4 は四次式を使用するか二次式を使用するかの判別値
// MINIMAM4 よりa(ax^4)の値が小さかったら二次式を使用します。
// MINIMAM2 は二次式を開放するc(c^2)の最小の値で、これより小さい場合は二次式の解法をしません。
// a の値が小さいときは b の値も小さくなります。
// 楕円の最大径を200にするスケールを使用するとa^4とb^3の指数の差が4程度になり、
// 最大径の設定値によつて指数の差がかわります。
// IMAGIMIN 四次式解放時の虚数判別 これより小さい場合は誤差として虚数として扱いません。
MINIMAM4 = 1E-17;
MINIMAM2 = 1E-14;
IMAGIMIN = 1E-8; // double の有効桁数15桁位の限度 誤差 0.0001 程度
// EMIN = 1E-15;
var
A3, A2, A1, A0 : extended;
b2, b1, b0 : extended;
e1, e0, e1s3, e0s2, e02s4, e13s27 : extended;
e02s4pe13s27 : extended;
r, rh1s3, cosQ, Q, cosQs3, sinQs3 : extended;
u, v, wiupv, t, c1, c0 : extended;
up, vm : string;
d1, d0, c1h2s4mc0, d1h2s4md0 : extended;
xim1, xim2, xim3, xim4 : string;
begin
Result := 0;
rh1s3 := 0;
sinQs3 := 0;
u := 0;
v := 0;
if (abs(a) > MINIMAM4) then begin
// a=0 の場合は四次方程式でないので解法不可
// x^4 + A3x^3 + A2x^2 + A1x + A0 = 0 に変換
A3 := b / a;
A2 := c / a;
A1 := d / a;
A0 := e / a;
// 四次式の解法
b2 := -3 / 8 * A3 * A3 + A2;
b1 := A3 * A3 * A3 / 8 - A3 * A2 / 2 + A1;
b0 := -3 / 256 * A3 * A3 * A3 * A3 + A3 * A3 * A2 / 16 - A3 * A1 / 4 + A0;
e1 := -b2 * b2 / 3 - 4 * b0;
e0 := -2 / 27 * b2 * b2 * b2 + 8 / 3 * b2 * b0 - b1 * b1;
e1s3 := e1 / 3;
e0s2 := e0 / 2;
e02s4 := e0s2 * e0s2;
e13s27 := e1s3 * e1s3 * e1s3;
e02s4pe13s27 := e02s4 + e13s27; // 判別式
//*---------------------------------------------------------------------------------
// if abs(e02s4pe13s27) < EMIN then e02s4pe13s27 := 0; // 小さな値はゼロ 桁落ち対策
if e02s4pe13s27 >= 0 then begin
u := -e0 / 2 + sqrt(e02s4pe13s27);
u := cube_root(u); // 立方根
v := -e0 / 2 - sqrt(e02s4pe13s27);
v := cube_root(v); // 立方根
wiupv := u + v;
end
else begin
r := sqrt(e02s4 + ABS(e02s4pe13s27)); // r > 0 e02s4 は必ずプラスかゼロなのでゼロ以下は無し
rh1s3 := power(r , 1/3);
if r <> 0 then begin
cosQ := -e0s2 / r;
Q := arccos(cosQ);
cosQs3 := cos(Q / 3);
sinQs3 := sin(Q / 3);
wiupv := 2 * rh1s3 * cosQs3;
u := rh1s3 * cosQs3;
v := u;
end
else
wiupv := 0;
end;
t := wiupv - 2 / 3 * b2; // t > 0
if t < 1E-11 then t := 0; // t がゼロ以下になるのは計算途中の桁落ち
c1 := sqrt(t);
if c1 <> 0 then begin
c0 := (c1 * c1 * c1 + b2 * c1 - b1) / 2 / c1;
if c0 <> 0 then d0 := b0 / c0
else d0 := 0;
end
else begin
if b2 * b2 - 4 * b0 > 0 then begin
c0 := (b2 + sqrt(b2 * b2 - 4 * b0)) / 2;
d0 := (b2 - sqrt(b2 * b2 - 4 * b0)) / 2;
end
else begin
c0 := b2 / 2;
d0 := c0;
end;
end;
d1 := - c1;
//*---------------------------------------------------------------------------------
if e02s4pe13s27 < 0 then begin
up := floatTostr(rh1s3 * sinQs3) + ' i'; // 複素数処理 textに変換
vm := floatTostr(rh1s3 * sinQs3) + ' i'; // 複素数処理 textに変換
end
else begin
up := '…';
vm := '…';
end;
c1h2s4mc0 := c1 * c1 / 4 - c0;
d1h2s4md0 := d1 * d1 / 4 - d0;
if abs(c1h2s4mc0) < IMAGIMIN then c1h2s4mc0 := 0; // 計算誤差修正
if abs(d1h2s4md0) < IMAGIMIN then d1h2s4md0 := 0; // 微小な複素数は許容
if c1h2s4mc0 >= 0 then begin
x1 := -c1 / 2 - A3 / 4 + sqrt(c1h2s4mc0); // x1
xim1 := '';
Result := Result or 1;
x2 := -c1 / 2 - A3 / 4 - sqrt(c1h2s4mc0); // x2
xim2 := '';
Result := Result or 2;
end
else begin
x1 := -c1 / 2 - A3 / 4; // x1
xim1 := ' + ' + floatTostr(sqrt(-c1h2s4mc0)) + ' i'; // 複素数処理 textに変換
x2 := -c1 / 2 - A3 / 4; // x2
xim2 := ' - ' + floatTostr(sqrt(-c1h2s4mc0)) + ' i'; // 複素数処理 textに変換
end;
if d1h2s4md0 >= 0 then begin
x3 := -d1 / 2 - A3 / 4 + sqrt(d1h2s4md0); // x3
xim3 := '';
Result := Result or 4;
x4 := -d1 / 2 - A3 / 4 - sqrt(d1h2s4md0); // x4
xim4 := '';
Result := Result or 8;
end
else begin
x3 := -d1 / 2 - A3 / 4; // x3
xim3 := ' + ' + floatTostr(sqrt(-d1h2s4md0)) + ' i'; // 複素数処理 textに変換
x4 := -d1 / 2 - A3 / 4; // x4
xim4 := ' - ' + floatTostr(sqrt(-d1h2s4md0)) + ' i'; // 複素数処理 textに変換
end;
image2.Canvas.TextOut(10, 150,'四次方程式の解法結果 デカルトの方法');
image2.Canvas.TextOut(20, 170,'x1= ' + floattostr(x1) + ' ' + xim1);
image2.Canvas.TextOut(20, 190,'x2= ' + floattostr(x2) + ' ' + xim2);
image2.Canvas.TextOut(20, 210,'x3= ' + floattostr(x3) + ' ' + xim3);
image2.Canvas.TextOut(20, 230,'x4= ' + floattostr(x4) + ' ' + xim4);
image2.Canvas.TextOut(20, 250, 'u= ' + floattostr(u) + ' + ' + up);
image2.Canvas.TextOut(20, 270, 'v= ' + floattostr(v) + ' - ' + vm);
end;
if (abs(a) <= MINIMAM4) and (abs(c) > MINIMAM2) then begin
// 二次方程式の解法
result := quadratic_equation(c, d, e, x1, x2, False);
end;
end;
// 楕円式にx,yの値を入れて検算
// 1になればx,yの値は正しいことになります。
function TForm1.Ellipse_judge(Ellipse: TEllipse; x, y: extended): boolean;
var
sx, sy, ba, bb : extended;
q, check : extended;
begin
result := false;
sx := x - Ellipse.fCx;
sy := y - Ellipse.fCy;
q := Ellipse.fAngle / 180 * pi;
ba := (sx * cos(q) + sy * sin(q)) / Ellipse.fRad_X;
bb := (-sx * sin(q) + sy * cos(q)) / Ellipse.fRad_Y;
check := ba * ba + bb * bb;
image2.Canvas.Brush.Style := bsSolid;
image2.Canvas.Brush.Color := clWhite;
image2.Canvas.FillRect(Rect(0, 430, 300, 450));
image2.Canvas.TextOut(10, 430, '楕円式検算 ' + floatTostr(check));
check := check - 1;
if abs(check) < 0.000001 then result := True;
if EllipCheck < check then EllipCheck := check;
end;
//------------------------------------------------
// 楕円弧上に交点があるかどうかの判定を行います
// Ellipse1 Ellipse2 楕円
// X 交点座標 X
// Y 交点座標 Y
//------------------------------------------------
function TForm1.intersection_judge(Ellipse1, Ellipse2: TEllipse; X, Y: extended): boolean;
var
qxy : extended;
endang : extended;
begin
result := Ellipse_judge(Ellipse1, x, y);
if not result then exit;
result := Ellipse_judge(Ellipse2, x, y);
if not result then exit;
result := False;
// 楕円弧１に対する交点の位置の角度計算
qxy := arctan2((y - Ellipse1.fCy),(x - Ellipse1.fCx)) / pi * 180 - Ellipse1.fAngle;
qxy := angle_amendment(qxy);
endang := Ellipse1.endAngle;
if Ellipse1.startAngle > Ellipse1.endAngle then begin
endang := Ellipse1.endAngle + 360;
if qxy < Ellipse1.startAngle then qxy := qxy + 360;
end;
// 楕円弧１の弧上に交点があるか判定
if (qxy >= Ellipse1.startAngle) and (qxy <= endang) or
(Ellipse1.startAngle = Ellipse1.endAngle) then else exit;
// 楕円弧２に対する交点の位置の角度計算
qxy := arctan2((y - Ellipse2.fCy),(x - Ellipse2.fCx)) / pi * 180 - Ellipse2.fAngle;
qxy := angle_amendment(qxy);
endang := Ellipse2.endAngle;
if Ellipse2.startAngle > Ellipse2.endAngle then begin
endang := Ellipse2.endAngle + 360;
if qxy < Ellipse2.startAngle then qxy := qxy + 360;
end;
// 楕円弧２の弧上に交点があるか判定
if (qxy >= Ellipse2.startAngle) and (qxy < endang) or
(Ellipse2.startAngle = Ellipse2.endAngle) then Result := True
else Result := False;
end;
//----------------------------------------------------
// 座標変換されている座標を元の座標にも戻します
// Xn, Yn 座標変換された座標
// defQ 座標変換角
// xo1, xo1 楕円１の中心座標
// x, y 元座標系の座標
//----------------------------------------------------
procedure TForm1.trance(Xn, Yn, defQ, xo1, yo1: extended; var x, y: extended);
var
xh, yh : extended;
stn : extended;
Q, Q1 : extended;
begin
Xn := Xn / scale;
Yn := Yn / scale;
Q := arctan2(Yn, Xn);
Q1 := Q - defQ;
stn := sqrt(xn * xn + yn * yn);
xh := cos(Q1) * stn;
yh := sin(Q1) * stn;
x := xh + xo1;
y := yh + yo1;
end;
var
Select : boolean; // タイマー停止用フラグ
//------------------------------------
// 二つの楕円の交点計算
//------------------------------------
function TForm1.cross_calc: boolean;
label
ANGLE;
const
Ftop = 330;
trnQ30 = 30;
k360 = 360;
k180 = 180;
k120 = 120;
k60 = 60;
K30 = 30;
k1E3 = 1000; // 丸め値
Qdf = 1E-3; // 丸めの値にあわせます
var
x : array[0..3] of extended;
y : array[0..3] of extended;
B3E3 : extended;
i, j, k, L, M, MB, N : integer;
xx : array[0..3] of extended;
yy : array[0..3] of extended;
xxo : array[0..3] of extended;
yyo : array[0..3] of extended;
xy : array[0..3] of byte;
A1, B1, C1, D1, E1, F1 : extended;
A2, B2, C2, D2, E2, F2 : extended;
A3, B3, D3, E3, F3 : extended;
A, B, C, D, E : extended;
xflag : byte;
dfq, qb, qn : extended;
nx, ny : extended;
stn : extended;
sq, tmq : extended;
df1, df2 : extended;
xob, yob : extended;
q1b, q2b : extended;
q1c, q2c : extended;
ar1, ar2, br1, br2 : extended;
qs30 : extended;
crossF : boolean;
angpF : boolean;
// 交点丸表示
procedure Ellips_ecross_Draw(x, y: extended);
begin
EllipseEx(image1.Canvas,
image1.Height,
3, // 線種細線
1, // 線幅
clblack, // 色黒
5, // 半径 a
5, // 半径 b
x * magnification - shift_x + draw_margin, // 中心座標
y * magnification - shift_y + draw_margin, // 中心座標
0, // 楕円角
0, // 開始角
360); // 終了角
end;
begin
// 座標変換 楕円１又は 楕円２の角度が30度になるようにして計算します。
if Ellipse1.fRad_X > Ellipse1.fRad_Y then df1 := Ellipse1.fRad_Y / Ellipse1.fRad_X
else df1 := Ellipse1.fRad_X / Ellipse1.fRad_Y;
if Ellipse2.fRad_X > Ellipse2.fRad_Y then df2 := Ellipse2.fRad_Y / Ellipse2.fRad_X
else df2 := Ellipse2.fRad_X / Ellipse2.fRad_Y;
// q1又はq2の角度から、0～180°の範囲の角度にします
// 補正角度を小さくするためです
q2b := Ellipse2.fAngle;
q1b := Ellipse1.fAngle;
// 0～180°の範囲になるように修正
repeat
if q1b >= k180 then q1b := q1b - k180;
if q1b < 0 then q1b := q1b + k180;
if q2b >= k180 then q2b := q2b - k180;
if q2b < 0 then q2b := q2b + k180;
until (q1b >= 0) and (q1b < k180) and (q2b >= 0) and (q2b < k180);
if df1 <= df2 then tmq := q1b
else tmq := q2b;
qs30 := q2b - q1b; // 楕円の角度差
if abs(qs30) < 0.5 then Timer1.Interval := 300 // 0.5 以下だったらタイマー300msec
else Timer1.Interval := 50; // タイマー50msec
nx := Ellipse2.fCx - Ellipse1.fCx;
ny := Ellipse2.fCy - Ellipse1.fCy;
qb := arctan2(ny, nx); // 楕円１と楕円２の中心位置角度
// 楕円１と２の位置の角度補正
// 30度との角度差
sq := trnQ30 - tmq; // 計算軸角修正値
if checkbox3.Checked then sq := 0; // テスト用 角度を入力角度にします
df1 := q1b + q2b;
if df1 < 1 then sq := sq + 1;
df1 := abs(q1b - q2b);
df2 := abs(df1 - K120);
if df2 < 1 then sq := sq + 1;
df2 := abs(df1 - K60);
if df2 < 1 then sq := sq + 1;
K := 0;
MB := 0;
N := 0;
ANGLE:
imageClear(1); // 値表示画面クリア
dfq := sq / 180 * pi; // 軸角変更値deg->rad
qn := qb + dfq; // 楕円1と楕円2の新しい中心位置角度
// 楕円１と２の角度補正
q1c := Ellipse1.fAngle;
q2c := Ellipse2.fAngle;
q2b := q2c + sq;
q1b := q1c + sq;
repeat
if q1b >= k180 then q1b := q1b - k180;
if q1b < 0 then q1b := q1b + k180;
if q2b >= k180 then q2b := q2b - k180;
if q2b < 0 then q2b := q2b + k180;
until (q1b >= 0) and (q1b < k180) and (q2b >= 0) and (q2b < k180);
ar1 := Ellipse1.fRad_X * scale;
br1 := Ellipse1.fRad_Y * scale;
ar2 := Ellipse2.fRad_X * scale;
br2 := Ellipse2.fRad_Y * scale;
// 楕円２の新しい座標計算
stn := sqrt(nx * nx + ny * ny);
xob := cos(qn) * stn * scale;
yob := sin(qn) * stn * scale;
// 楕円式の変換
quadratic_transform(ar1, br1, 0, 0, q1b, A1, B1, C1, D1, E1, F1);
quadratic_transform(ar2, br2, xob, yob, q2b, A2, B2, C2, D2, E2, F2);
// y^2 の消去
A3 := A1 / C1 - A2 / C2;
B3 := B1 / C1 - B2 / C2;
D3 := D1 / C1 - D2 / C2;
E3 := E1 / C1 - E2 / C2;
F3 := F1 / C1 - F2 / C2;
// 四次式の係数を求めます
// Ax^4 + Bx^3 + Cx^2 + Dx + E = 0;
A := A1*B3*B3 - A3*B1*B3 + A3*A3*C1;
B := 2*A1*B3*E3 + 2*A3*C1*D3 + B3*B3*D1 - A3*B1*E3 - B1*B3*D3 - A3*B3*E1;
C := A1*E3*E3 + 2*A3*C1*F3 + D3*D3*C1 + 2*B3*D1*E3 + B3*B3*F1 - B1*B3*F3
- B1*D3*E3 - A3*E1*E3 - B3*D3*E1;
D := 2*C1*D3*F3 + D1*E3*E3 + 2*B3*E3*F1 - B3*E1*F3 - D3*E1*E3 - B1*E3*F3;
E := C1*F3*F3 + E3*E3*F1 - E1*E3*F3;
image2.Canvas.Brush.Style := bsClear;
// 連立方程式の係数表示
image2.Canvas.TextOut(10, 5, '連立方程式の係数');
image2.Canvas.TextOut(20, 20, 'A= ' + floatTostr(A));
image2.Canvas.TextOut(20, 35, 'B= ' + floatTostr(B));
image2.Canvas.TextOut(20, 50, 'C= ' + floatTostr(C));
image2.Canvas.TextOut(20, 65, 'D= ' + floatTostr(D));
image2.Canvas.TextOut(20, 80, 'E= ' + floatTostr(E));
image2.Canvas.TextOut(20, 100, 'B3= ' + floatTostr(B3));
image2.Canvas.TextOut(20, 115, 'E3= ' + floatTostr(E3));
image2.Canvas.TextOut(10, 500, '交点計算時楕円の角度');
image2.Canvas.TextOut(20, 515, 'q1b= ' + floatTostr(q1b) + '°');
image2.Canvas.TextOut(20, 530, 'q2b= ' + floatTostr(q2b) + '°');
result := false;
// 四次 二次式の解法
for L := 0 to 3 do begin
x[L] := 0;
y[L] := 0;
end;
if checkbox1.Checked then
xflag := newcross_quadratic(a, b, c, d, e, x[0], x[1], x[2], x[3]) // フェラーリ
else
xflag := cross_quadratic(a, b, c, d, e, x[0], x[1], x[2], x[3]); // デカルト
i := 1;
j := -1;
// 交点があったら
// 交点のあるx座標の取り出し
if xflag <> 0 then begin
for L := 0 to 3 do begin
if xflag and i = i then begin
inc(j);
xx[j] := x[L];
end;
i := i * 2;
end;
end;
M := 0;
angpF :=False;
// 近似するx座標の検索
for L := 0 to j do
for i := L + 1 to j do begin
B3E3 := abs(xx[L] - xx[i]); // x座標の差分
if B3E3 < Qdf * scale then begin // 指定値より小さかったら
inc(M); // 数のカウント
angpF :=true; // フラグセット
end;
end;
// 近似するx座標があったら計算角度を変更して再計算
// 三回変更しても変わらなければ、又は、近似する数が減少すれば次へ
if angpF then begin
if MB = M then inc(K); // 近似するxの組数が同じだったらインクリメント
if k <= 3 then begin
MB := M; // 組数保存
sq := sq + 1; // 計算角度変更
goto ANGLE; // 方程式の解法再計算
end;
end;
image2.Canvas.TextOut(10, 467, '重複するXの値の数 ＝ ' + inttostr(M));
image2.Canvas.TextOut(10, 484, ' Loop数 ＝ ' + inttostr(N));
// x座標よりy座標の計算
// 分母がゼロでないか確認して計算、分母がゼロは無いはずだが桁落ち対策として一応確認
i := 1;
if xflag <> 0 then begin
for L := 0 to 3 do begin
if xflag and i = i then begin
B3E3 := abs(B3 * x[L] + E3);
if B3E3 > 0 then // 分母がゼロでないか確認
y[L] := - (A3 * x[L] * x[L] + D3 * x[L] + F3) / (B3 * x[L] + E3)
else xflag := xflag and ($FF - i);
end;
i := i * 2;
end;
end
else result := true;
// 計算結果の表示 座標は元の座標に戻します
for j := 0 to 3 do begin
xx[j] := 0;
yy[j] := 0;
xy[j] := 0;
end;
i := -1; // 交点の数 -1 がゼロ
image2.Canvas.TextOut( 10, Ftop,'交点の座標');
crossF := False;
j := 1;
EllipCheck := 0; // 1との差クリア
for L := 0 to 3 do begin
if xflag and j = j then begin // j=1,2,4,8
trance(x[L], y[L], dfQ, Ellipse1.fCx, Ellipse1.fCy, x[L], y[L]); // 座標変換 元の座標に戻します
if intersection_judge(Ellipse1, Ellipse2, x[L], y[L]) then begin // 楕円弧上か確認
inc(i); // 交点の数カウント
xx[i] := x[L];
yy[i] := y[L];
Ellips_ecross_Draw(x[L], y[L]); // 交点丸表示
crossF := True;
end;
end;
j := j * 2;
end;
// 有効な交点があったら
if xflag > 0 then begin
for j := 0 to i do xy[j] := 0;
for j := 0 to i do begin
xx[j] := round(xx[j] * 1000) / 1000; // 小数点四桁以下丸め
yy[j] := round(yy[j] * 1000) / 1000;
end;
// 重複する交点検索 重複していたら xy[] > 0
for j := 0 to i do begin
for k := j + 1 to i do begin
if (xx[j] = xx[k]) and (yy[j] = yy[k]) then begin
inc(xy[K]); // 重複フラグセット 重複 > 0
end;
end;
end;
// 重複した交点の削除
k := -1;
for j := 0 to i do
if xy[j] = 0 then begin
inc(k);
xxo[k] := xx[j];
yyo[k] := yy[j];
end;
// 交点の座標表示
for j := 0 to k do begin
i := Ftop + 20 * (j + 1);
image2.Canvas.TextOut( 20, i, 'x' + inttostr(j + 1) + '=' + floatTostrF(xxo[j],ffFixed,10,3));
image2.Canvas.TextOut(220, i, 'y' + inttostr(j + 1) + '=' + floatTostrF(yyo[j],ffFixed,10,3));
end;
end;
if not crossF and CheckBox2.Checked then Select := False; // 交点がなかったらタイマー停止
end;
//--------------------------------------------------------
// 入力された楕円の描画
// 楕円作図のy方向は、楕円作図ルーチンで修正されます。
//--------------------------------------------------------
procedure TForm1.inputdata_drawing;
const
CONTR = 200;
var
left_min, left_max : extended;
top_min, top_max : extended;
all_width, all_height : extended;
ac1, ac2 : extended;
x1, x2, y1, y2 : extended;
dx1, dy1, dq1 : extended;
dx2, dy2, dq2 : extended;
begin
// 楕円の半径の大きい方選択
ac1 := Ellipse1.fRad_X;
if Ellipse1.fRad_X < Ellipse1.fRad_Y then begin
ac1 := Ellipse1.fRad_Y;
end;
ac2 := Ellipse2.fRad_X;
if Ellipse2.fRad_X < Ellipse2.fRad_Y then begin
ac2 := Ellipse2.fRad_Y;
end;
// 半径を一定の値で計算する為のスケール設定
// CONTRの値を変更した場合は、四次二次連立方程式の判別値 MINIMAM4, MINIMAM2 も変更する必要があります。
if ac2 > ac1 then scale := CONTR / ac2
else scale := CONTR / ac1;
// scale := 1;
// 作図範囲の設定
left_min := Ellipse1.fCx - ac1;
if Ellipse2.fCx - ac2 < left_min then left_min := Ellipse2.fCx - ac2;
left_max := Ellipse1.fCx + ac1;
if Ellipse2.fCx + ac2 > left_max then left_max := Ellipse2.fCx + ac2;
all_width := left_max - left_min;
top_min := Ellipse1.fcy - ac1;
if Ellipse2.fCy - ac2 < top_min then top_min := Ellipse2.fCy - ac2;
top_max := Ellipse1.fcy + ac1;
if Ellipse2.fCy + ac2 > top_max then top_max := Ellipse2.fCy + ac2;
all_height := top_max - top_min;
top_max := (image1.Height - draw_margin * 2) / all_Height;
magnification := (image1.Width - draw_margin * 2) / all_width;
if magnification > top_max then magnification := top_max;
shift_x := left_min * magnification;
shift_y := top_min * magnification;
// イメージクリア
imageClear(0);
// 楕円作図
x1 := Ellipse1.fCx * magnification - shift_x + draw_margin;
y1 := Ellipse1.fCy * magnification - shift_y + draw_margin;
x2 := Ellipse2.fCx * magnification - shift_x + draw_margin;
y2 := Ellipse2.fCy * magnification - shift_y + draw_margin;
// 楕円１作図
EllipseEx(image1.Canvas,
image1.Height, // canvas高さ
3, // 線種
1, // 線幅
clRed, // 色
Ellipse1.fRad_X * magnification, // 半径a
Ellipse1.fRad_Y * magnification, // 半径b
x1, // 中心位置x
y1, // 中心位置y
Ellipse1.fAngle, // 回転角 deg
Ellipse1.startAngle, // 作図開始角
Ellipse1.endAngle); // 作図終了角
EllipseEx(image1.Canvas, image1.Height, 0, 1, clRed,
Ellipse1.fRad_X * magnification, Ellipse1.fRad_Y * magnification,
x1, y1,
Ellipse1.fAngle,
Ellipse1.endAngle, Ellipse1.startAngle);
// 楕円２作図
EllipseEx(image1.Canvas, image1.Height, 3, 1, clBlue,
Ellipse2.fRad_X * magnification, Ellipse2.fRad_Y * magnification,
x2, y2,
Ellipse2.fAngle,
Ellipse2.startAngle, Ellipse2.endAngle);
EllipseEx(image1.Canvas, image1.Height, 0, 1, clBlue,
Ellipse2.fRad_X * magnification, Ellipse2.fRad_Y * magnification,
x2, y2,
Ellipse2.fAngle,
Ellipse2.endAngle, Ellipse2.startAngle);
// 中心線作図
dq1 := Ellipse1.fAngle / 180 * pi;
dx1 := cos(dq1) * 30;
dy1 := sin(dq1) * 30;
dq2 := (90 + Ellipse1.fAngle) / 180 * pi;
dx2 := cos(dq2) * 30;
dy2 := sin(dq2) * 30;
StraightLineDraw(image1.Canvas, image1.Height, 1, 1, clRed,
x1 - dx1, y1 - dy1, x1 + dx1, y1 + dy1, true);
StraightLineDraw(image1.Canvas, image1.Height, 1, 1, clRed,
x1 - dx2, y1 - dy2, x1 + dx2, y1 + dy2, true);
dq1 := Ellipse2.fAngle / 180 * pi;
dx1 := cos(dq1) * 30;
dy1 := sin(dq1) * 30;
dq2 := (90 + Ellipse2.fAngle) / 180 * pi;
dx2 := cos(dq2) * 30;
dy2 := sin(dq2) * 30;
StraightLineDraw(image1.Canvas, image1.Height, 1, 1, clBlue,
x2 - dx1, y2 - dy1, x2 + dx1, y2 + dy1, true);
StraightLineDraw(image1.Canvas, image1.Height, 1, 1, clBlue,
x2 - dx2, y2 - dy2, x2 + dx2, y2 + dy2, true);
end;
//----------------------------------
// 角度の範囲０から360の範囲に調整
//----------------------------------
function TForm1.angle_amendment(angle : extended): extended;
begin
repeat
if angle >= 360 then angle := angle - 360;
if angle < 0 then angle := angle + 360;
until (angle < 360) and (angle >= 0);
Result := angle;
end;
procedure TForm1.Button1Click(Sender: TObject);
begin
if TimeF then begin
TimeF := False;
Button1.Caption := 'Auto Start';
end
else begin
TimeF := True;
Button1.Caption := 'Auto Stop';
end;
if TimeF then Timer1.Enabled := true;
end;
procedure TForm1.Timer1Timer(Sender: TObject);
var
q1, q2 : extended;
ch : integer;
begin
Timer1.Enabled := False;
if not Select and checkbox2.Checked then begin
TimeF := False;
exit;
end;
val(angle_q1_Edit.Text, q1, ch);
if ch <> 0 then exit;
val(angle_q2_Edit.Text, q2, ch);
if ch <> 0 then exit;
if q1 < 0.02 then q1 := q1 + 0.00005
else q1 := q1 + 0.125;
if q1 >= 360 then q1 := 0;
if q2 < 0.02 then q2 := q2 + 0.0001
else q2 := q2 + 0.25;
if q2 >= 359.99 then begin
if q1 <> 0 then q2 := 359.99
else q2 := 0;
end;
angle_q1_Edit.Text := floatTostr(q1);
angle_q2_Edit.Text := floatTostr(q2);
SelectBtnClick(nil);
if not Select then begin
TimeF := False;
exit;
end;
if TimeF then Timer1.Enabled := True;
end;
//--------------------
// 入力処理と計算開始
//--------------------
procedure TForm1.SelectBtnClick(Sender: TObject);
const
k360 = 360;
var
ch: integer;
begin
Select := false;
// 楕円１のデーター
val(radius_a1_Edit.Text, Ellipse1.fRad_X, ch);
if ch <> 0 then begin
application.MessageBox('楕円１の半径a１数値ではありません。', '楕円１の半径a１', 0);
exit;
end;
if Ellipse1.fRad_X <= 0 then begin
application.MessageBox('楕円１の半径a１がゼロ 又はゼロ以下です。', '楕円１の半径a１', 0);
exit;
end;
val(radius_b1_Edit.Text, Ellipse1.fRad_Y, ch);
if ch <> 0 then begin
application.MessageBox('楕円１の半径b１数値ではありません。', '楕円１の半径b１', 0);
exit;
end;
if Ellipse1.fRad_Y <= 0 then begin
application.MessageBox('楕円１の半径b１がゼロ 又はゼロ以下です。', '楕円１の半径b１', 0);
exit;
end;
val(Center_x1_Edit.Text, Ellipse1.fCx, ch);
if ch <> 0 then begin
application.MessageBox('楕円１の中心位置x１数値ではありません。', '楕円１の中心位置x１', 0);
exit;
end;
val(Center_y1_Edit.Text, Ellipse1.fCy, ch);
if ch <> 0 then begin
application.MessageBox('楕円１の中心位置y１数値ではありません。', '楕円１の中心位置y１', 0);
exit;
end;
val(angle_q1_Edit.Text, Ellipse1.fAngle, ch);
if ch <> 0 then begin
application.MessageBox('楕円１の角度θ１数値ではありません。', '楕円１の角度θ１', 0);
exit;
end;
val(Start_angle_S1.Text, Ellipse1.startAngle, ch);
if ch <> 0 then begin
application.MessageBox('楕円１の開始角数値ではありません。', '楕円１の開始角S1', 0);
exit;
end;
val(End_angle_E1.Text, Ellipse1.endAngle, ch);
if ch <> 0 then begin
application.MessageBox('楕円１の終了角数値ではありません。', '楕円１の終了角E1', 0);
exit;
end;
// 楕円２のデーター
val(radius_a2_Edit.Text, Ellipse2.fRad_X, ch);
if ch <> 0 then begin
application.MessageBox('楕円２の半径a２数値ではありません。', '楕円２の半径a２', 0);
exit;
end;
if Ellipse2.fRad_X <= 0 then begin
application.MessageBox('楕円２の半径a２がゼロ 又はゼロ以下です。', '楕円２の半径a２', 0);
exit;
end;
val(radius_b2_Edit.Text, Ellipse2.fRad_Y, ch);
if ch <> 0 then begin
application.MessageBox('楕円２の半径b２数値ではありません。', '楕円２の半径b２', 0);
exit;
end;
if Ellipse2.fRad_Y <= 0 then begin
application.MessageBox('楕円２の半径b２がゼロ 又はゼロ以下です。', '楕円２の半径b２', 0);
exit;
end;
val(Center_x2_Edit.Text, Ellipse2.fCx, ch);
if ch <> 0 then begin
application.MessageBox('楕円２の中心位置x２数値ではありません。', '楕円２の中心位置x２', 0);
exit;
end;
val(Center_y2_Edit.Text, Ellipse2.fCy, ch);
if ch <> 0 then begin
application.MessageBox('楕円２の中心位置y２数値ではありません。', '楕円２の中心位置y２', 0);
exit;
end;
val(angle_q2_Edit.Text, Ellipse2.fAngle, ch);
if ch <> 0 then begin
application.MessageBox('楕円２の角度θ２数値ではありません。', '楕円２の角度θ２', 0);
exit;
end;
val(Start_angle_S2.Text, Ellipse2.startAngle, ch);
if ch <> 0 then begin
application.MessageBox('楕円２の開始角数値ではありません。', '楕円２の開始角S2', 0);
exit;
end;
val(End_angle_E2.Text, Ellipse2.endAngle, ch);
if ch <> 0 then begin
application.MessageBox('楕円２の終了角数値ではありません。', '楕円２の終了角E2', 0);
exit;
end;
Select := True;
// 入力された楕円角度の値修正 0 ～ 360 の範囲に入る様にします。
Ellipse1.fAngle := angle_amendment(Ellipse1.fAngle);
Ellipse2.fAngle := angle_amendment(Ellipse2.fAngle);
Ellipse1.startAngle := angle_amendment(Ellipse1.startAngle);
Ellipse1.endAngle := angle_amendment(Ellipse1.endAngle);
Ellipse2.startAngle := angle_amendment(Ellipse2.startAngle);
Ellipse2.endAngle := angle_amendment(Ellipse2.endAngle);
// 入力値の画像表示
inputdata_drawing;
// 交点の計算
cross_calc;
end;
//-----------
// 初期設定
//-----------
procedure TForm1.FormCreate(Sender: TObject);
begin
Clientheight := 554;
ClientWidth := 1307;
top := (screen.Height - height) div 2;
left := (screen.Width - width) div 2;
// 線種配列确保
setlength(LPitch, LineN);
// 線種データーセット
LPitch[0].segment := 2; // 破線
LPitch[0].Pitch[0] := 6;
LPitch[0].Pitch[1] := 3;
LPitch[1].segment := 4; // １点鎖線
LPitch[1].Pitch[0] := 15;
LPitch[1].Pitch[1] := 3;
LPitch[1].Pitch[2] := 3;
LPitch[1].Pitch[3] := 3;
LPitch[2].segment := 6; // ２点鎖線
LPitch[2].Pitch[0] := 18;
LPitch[2].Pitch[1] := 3;
LPitch[2].Pitch[2] := 3;
LPitch[2].Pitch[3] := 3;
LPitch[2].Pitch[4] := 3;
LPitch[2].Pitch[5] := 3;
// イメージクリア
imageClear(0);
image2.Canvas.Font.Name := 'ＭＳ ゴシック';
// image2.Canvas.Font.Style := [fsbold];
image2.Canvas.Font.Height := 13;
Button1.Caption := 'Auto Start';
end;
end.
Ellipses_Node_New.zip