楕円と楕円の交点 その1
2017/06/12 プログラムの修正
1.楕円弧に対応しました 楕円の開始角と終了角の範囲以外の交点は表示しない様にしました。
2.楕円の縦横変倍が出来なかったので、縦横変倍が出来る様にして、少し計算速度を上げました。
楕円と楕円の交点を求める計算プログラムですが、インターネットで探しても、情報はあまりありません。
交点を求める方法としては、二つの楕円上の点の距離を計算して、近似的に交点を求める方法と、楕円二元二次方程式の連立方程式を解法して求める方法があります。
近似的に求めるにしても、連立方程式により求める方法にしても、単純には計算が出来ません。
方程式には、問題が無くても、実際に計算する場合は、有効桁数があり、桁落ちの問題が発生し、正しい答えが出ない場合が間々あります。
此処での計算は、楕円上の点の距離を計算し、距離が0になる点を交点とする方法です。
連立方程式を解く必要がないので、それなりに簡単に交点を求めることが出来ますが、精度をどの程度必要とするかです。
精度を高くすれば、計算に時間がかかると同時に、桁落ちが発生して、交点を見つけることが出来なくなります。
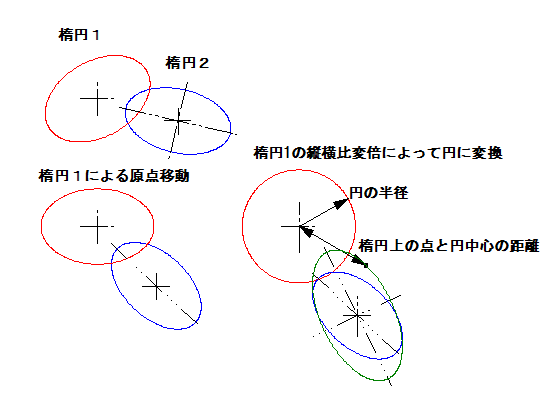
左図、楕円1と、楕円2は、角度を持った縦横比自由な楕円です。
楕円状の点の距離を計算するのには、片方を原点に置き、角度も0度にして、縦横比の変倍をして、円に変換するのが一番簡単に計算が出来ます。
円に変換をしなくても、計算は出来ますが、近似点を求めるのに沢山の計算をする為、近似点を求める計算を少なくしています。
片方の楕円を円に変換をすると、円に変換できなかった楕円側の楕円上の点と、円の中心からの距離から、円の半径を引き、0になる点が交点となります。
楕円1を円に変換した時に、円の中心に対する、楕円2の中心位置も、楕円1の縦横比分だけ変化しく、楕円2も縦横比分の変化をします。
計算の桁落ちを一定に保つため、楕円の最大半径が一定の値になるように、スケール変換をして計算します。
楕円2は座標変換後も角度を持っているので、連立方程式を解いて新しい楕円を求めています。
新しい楕円を求めなくても、縦横比から楕円上の座標を求める事が出来ますが、その分計算が増加します。
交点の検出は、楕円2の楕円上の点の計算時、計算角度θを少しづつ変化させ、円の半径との距離の符号が変化した場合、交点を通過したことになるので、前の角度θにもどし、今度は前よりも少しづつ角度θを変化させる事を繰り返すことで、必要とする精度まで変化させる角度⊿θが小さくなったら、交点とします。
交点を検出した位置が、交点の検出開始した位置に戻っていなかったら、次の交点の検出をおこない、検出開始の位置へ戻ったら終了とします。
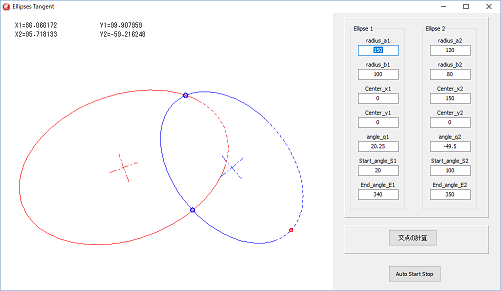
青い楕円上の赤い点が、交点検索開始点です。
楕円1の円としても距離の差が一番大きくなる場所から検索を開始し、楕円2を一周したら検索終了です。
楕円弧として、楕円の開始角と、終了角を指定していますが、これ以外の交点については、表示をしません。
プログラム
プログラムには、作図ルーチンがあり、Delphiの作図ではなく、専用の作図ルーチンを使用しています。
角度のある楕円を自由に作図するためです。
unit MainG;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.ExtCtrls, Vcl.StdCtrls, Vcl.Buttons, math,
Vcl.Mask;
type
TELLIPSE = record
fRad_X : Extended; // X 方向半径
fRad_Y : Extended; // Y 方向半径
fAngle : Extended; // 楕円角度
fCx : Extended; // 楕円中心位置 X
fcy : Extended; // 楕円中心位置 Y
startAngle : Extended; // 開始角
endAngle : Extended; // 終了角
end;
TForm1 = class(TForm)
Panel1: TPanel;
Ellipse1Box: TGroupBox;
radius_a1_Edit: TLabeledEdit;
radius_b1_Edit: TLabeledEdit;
Center_x1_Edit: TLabeledEdit;
Center_y1_Edit: TLabeledEdit;
angle_q1_Edit: TLabeledEdit;
Ellipse2Box: TGroupBox;
radius_a2_Edit: TLabeledEdit;
radius_b2_Edit: TLabeledEdit;
Center_x2_Edit: TLabeledEdit;
Center_y2_Edit: TLabeledEdit;
angle_q2_Edit: TLabeledEdit;
Panel2: TPanel;
SelectBtn: TBitBtn;
Image1: TImage;
Start_angle_S1: TLabeledEdit;
Start_angle_S2: TLabeledEdit;
End_angle_E1: TLabeledEdit;
End_angle_E2: TLabeledEdit;
procedure FormCreate(Sender: TObject);
procedure SelectBtnClick(Sender: TObject);
private
{ Private 宣言 }
procedure imageClear;
function Dist(x1, y1, x2, y2 : Extended): Extended;
function Angle(dx, dy: Extended): Extended ;
procedure LineSub(Tcv: TCanvas; px1, py1, px2, py2: Extended);
procedure pitchControl(NLine, LW: integer);
procedure LineSubPitch(Tcv : TCanvas; Ln: integer; var i: integer; var d1: Extended; px1, py1, px2, py2: Extended);
function angleSe(a, b, rad: Extended): Extended;
procedure EllipseEx(Tcv: TCanvas; h, lf, lw: integer; lc: Tcolor; a, b, x, y, rq, sq, eq: Extended);
procedure EllipseXY(ar, br, xoc, yoc, qb, q: Extended; var X, Y: Extended);
procedure inputdata_drawing;
procedure cross_calc;
function EllipseCircleDistance(ar1, xbc, ybc, ar, br, qbc, q: Extended; var X, Y: Extended): Extended;
function Start_End_Angle(seAngle, Angle, XScale, Yscale, nAngle: Extended): Extended;
function Ellipse_magnification(Ellipse: TELLIPSE; XScale, YScale: Extended): TELLIPSE;
function intersection_judge(Ellipse1, Ellipse2: TEllipse; X, Y: Extended): boolean;
function angle_amendment(angle : Extended): Extended;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
const
PitchN = 5; // 線ピッチ設定数
LineN = 3; // 線種数
LIMIT8 = 0.00000001;
type
TLinePitch = Record // 線種用レコード
Pitch : array[0..PitchN] of Extended; // ピッチ 線長さ 空白の繰り返し
segment : integer; // ピッチ数
End;
var
LPitch : array of TLinePitch; // 線種用 (線ピッチ)
VPitch : array[0..PitchN] of Extended; // 線幅による線ピッチ設定用
magnification : Extended; // 表示倍率
Ellipse1 : TELLIPSE; // 楕円1
Ellipse2 : TELLIPSE; // 楕円2
shift_x: Extended; // 表示X方向ずらし量
shift_y: Extended; // 表示Y方向ずらし量
const
draw_margin = 30; // 左右上下作図マージン
//---------------------
// 画像表示部クリア
//---------------------
procedure TForm1.imageClear;
begin
image1.Canvas.Brush.Style := bsSolid;
image1.Canvas.Brush.Color := clWhite;
image1.Canvas.FillRect(Rect(0, 0, image1.Width, image1.Height));
end;
//-----------------------------------------------
// 線幅によるピッチの補正
// 線幅を広くするとスペースが狭くなるので広げます
// NLine 線種
// LW 線幅
//-----------------------------------------------
procedure TForm1.pitchControl(NLine, LW: integer);
var
i : integer;
begin
// 線幅によるピッチの補正
for i := 0 to pitchN do begin
if i mod 2 <> 0 then // 奇数配列noセグメントがスペース
Vpitch[i] := LPitch[NLine].Pitch[i] + LW // スペースに線幅加算
else
Vpitch[i] := LPitch[NLine].Pitch[i];
end;
end;
//----------------------------
// 作図用 二点間線引き
//----------------------------
procedure TForm1.LineSub(Tcv: TCanvas; px1, py1, px2, py2: Extended);
var
x1, y1, x2, y2 : integer ;
begin
x1 := Round(px1);
y1 := Round(py1);
x2 := Round(px2);
y2 := Round(py2);
Tcv.MoveTo(x1, y1);
Tcv.LineTo(x2, y2);
end;
//----------------------
// 距離(長さ)を計算
// x1, y1 : 始点
// x2, y2 : 終点
// out : 距離(長さ)
//----------------------
function TForm1.Dist(x1, y1, x2, y2 : Extended): Extended ;
begin
Result := Sqrt((x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1)) ;
end;
//--------------------------------
// 角度を計算[rad]
// dx : X方向差分
// dy : Y方向差分
// out: 角度 (0~2 * Pi)
//--------------------------------
function TForm1.Angle(dx, dy: Extended): Extended ;
var
r : Extended ;
begin
Result := 0.0;
if (Abs(dx) < LIMIT8) and (Abs(dy) < LIMIT8) then exit;
r := ArcTan2(dy, dx);
if r < 0.0 then r := r + 2.0 * Pi;
Result := r;
end;
//--------------------------------------
// 線分の表示・サブ2:線種指定
// Ln : 線種番号(1-)
// i : 開始セグメント番号(終了時更新)
// d1 : 開始ピッチ長さ (終了時更新)
// px1, py1 : 線分始点[mm]
// px2, py2 : 線分終点[mm]
//--------------------------------------
procedure TForm1.LineSubPitch(Tcv: TCanvas; Ln: integer; var i: integer; var d1: Extended; px1, py1, px2, py2: Extended);
var
x1, y1, x2, y2 : Extended;
a, sa, ca, d, p : Extended;
PenStyle : TPenstyle;
begin
PenStyle := Tcv.Pen.Style; // 線種バックアップ
Tcv.Pen.Style := psSolid;
if (Ln < 0) or (Ln >= LineN) then begin // 無い線種は実線
LineSub(Tcv, px1, py1, px2, py2);
Tcv.Pen.Style := PenStyle; // 線種戻し
exit;
end;
a := Angle(px2 - px1, py2 - py1); // 角度計算
d := Dist(px1, py1, px2, py2); // 距離計算
ca:= Cos(a); // コサイン
sa:= Sin(a); // サイン
x1:= px1; // 始点x
y1:= py1 ; // 始点y
repeat
p := Vpitch[i] - d1; // ピッチと開始ピッチ長さ差分 残り分
if (p > d) then p := d; // 距離より残り分が大きい場合 距離
x2 := x1 + p * ca ; // 新しい位置計算
y2 := y1 + p * sa ;
if (i mod 2) = 0 then // セグメント偶数毎に線引き 空白部線引きしない
LineSub(Tcv, x1, y1, x2, y2);
x1 := x2; // 終点を始点にセット
y1 := y2;
d := d - p ; // 残り長さ計算
if d > LIMIT8 then begin // 残り長さがあったら
d1 := 0.0; // 開始ピッチ長さクリア
Inc(i); // セグメントカウンターインクリメント
if i >= LPitch[Ln].segment then i := 0; // セグメント数を超えたらゼロに戻し
end;
until d <= LIMIT8;
d1 := d1 + p; // 開始ピッチ長さ
Tcv.Pen.Style := PenStyle; // 線種戻し
end;
//------------------------------------------
// 楕円の開始角を 基礎円の開始角に変換
//------------------------------------------
function TForm1.angleSe(a, b, rad: Extended): Extended;
const
KMIN = 0.00000001;
var
l : Extended;
begin
// 90°, 270°, 0°, 180° 360°近傍は計算しない
if (abs(rad - pi / 2) < KMIN) or (abs(rad - pi - pi / 2) < KMIN)
or (abs(rad) < KMIN) or (abs(rad - pi) < KMIN) or
(abs(rad - pi * 2) < KMIN)
then begin
result := rad;
exit;
end;
// 底辺の長さ計算 ( b / a の値がいつも正の値なので元の角度によって角度を補正)
// 分母がゼロに近くなる時もあるので、判別が不要なarctan2を使用します
l := b / a / tan(rad);
// 180°以下だったら
if rad < pi then
result := arctan2(1, l)
else
// 360°以下だったら
if rad < pi * 2 then
result := arctan2(1, l) + pi
// 360°を超えていたら
else
result := arctan2(1, l) + pi * 2;
end;
//-------------------------------------------------------------------
// ar, br 楕円半径
// xoc, yoc 楕円中心位置
// qb 楕円角度 rad 単位
// q 角度位置 rad 単位
// x, y 角度q時の楕円上の座標
// x = a * cos(q) * cos(qb) - br * sin(q) * sin(qb) + xo; 座標 x
// y = a * cos(q) * sin(qb) + br * sin(q) * cos(qb) + yo; 座標 y
//-------------------------------------------------------------------
procedure TForm1.EllipseXY(ar, br, xoc, yoc, qb, q: Extended; var X, Y: Extended);
var
cosq, sinq, cosqbc, sinqbc: Extended;
arc, brs : Extended;
begin
cosq := cos(q);
sinq := sin(q);
cosqbc := cos(qb);
sinqbc := sin(qb);
arc := ar * cosq;
brs := br * sinq;
X := xoc + arc * cosqbc - brs * sinqbc; // 座標 x
Y := yoc -(arc * sinqbc + brs * cosqbc); // 座標 y WindowはY座標方向が逆のためマイナス
// yoc は Window座標に変換済みです
end;
//---------------------------------------
// 楕円の描画
// Windows為ののy方向変換は,このルーチンで行います。
// tcv 描画キャンバスの指定
// h キャンバスの高さ
// lf 線の種類
// lw 線の幅
// lc 線の色
// a 半径a
// b 半径b
// x 中心位置 x
// y 中心位置 y
// rq 楕円の角度
// sq 描画開始角
// eq 描画終了
//---------------------------------------
procedure TForm1.EllipseEx(Tcv : TCanvas; h, lf, lw: integer; lc: Tcolor; a, b, x, y, rq, sq, eq: Extended);
var
sqrad, eqrad : Extended;
qrad : Extended;
Ssqrad, Seqrad : Extended;
sp : integer;
dq : Extended;
d1 : Extended;
dp : integer;
px1, py1 : Extended;
px2, py2 : Extended;
i : integer;
begin
Tcv.Pen.Width := lw;
Tcv.Pen.Color := lc;
// y方向変換
y := h - y;
// 線幅によるピッチの補正
pitchControl(lf, lw);
// 終了角と開始角が一致したら全周
if abs(sq - eq) < LIMIT8 then begin
sq := 0;
eq := 360;
end;
// 分割数 半径に応じて調整
sp := round(sqrt(a + b) * 4); // 分割数
// 楕円の計算と描画
sqrad := sq / 180 * pi;
eqrad := eq / 180 * pi;
qrad := pi / 180 * rq; // 回転角 ラジアン
Ssqrad := angleSe(a, b, sqrad); // 基本円角度に変換
Seqrad := angleSe(a, b, eqrad); // 基本円角度に変換
// 分割微小角計算 分割数角度で補正
if Seqrad >= Ssqrad then begin
sp := round(sp * (Seqrad - Ssqrad) / pi);
if sp = 0 then sp := 1;
dq := (Seqrad - Ssqrad) / sp // 分割微小角 ラジアン
end
else begin
sp := round(sp * (Pi * 2 - Ssqrad + Seqrad) / pi);
if sp = 0 then sp := 1;
dq := (Pi * 2 - Ssqrad + Seqrad) / sp; // 分割微小角 ラジアン
end;
// 開始点の計算
d1 := 0; // 長さ
dp := 0; // セグメント位置
// px1 py1 開始座標
EllipseXY(a, b, x, y, qrad, Ssqrad, px1, py1);
// 分割数分計算繰り返し描画
for i := 1 to sp do begin
// px2 py2 終点座標
EllipseXY(a, b, x, y, qrad, Ssqrad + dq * i, px2, py2);
// ピッチ線描画
LineSubPitch( // ピッチ線描画
tcv, // TCanvas
lf, // 線種
dp, // セグメント位置
d1, // 長さ
px1, // 始点X
py1, // 始点Y
px2, // 終点X
py2 // 終点Y
);
px1 := px2; // 終点Xを始点Xに
py1 := py2; // 終点Yを始点Yに
end;
end;
//-------------------------------------
// 変倍後の楕円の開始終了角の計算
// seAngle 楕円の開始終了角
// Angle 変倍前の楕円の角度
// XScale 横変倍率
// YScale 縦変倍率
// nAngle 変倍後の楕円の角度
//-------------------------------------
function TForm1.Start_End_Angle(seAngle, Angle, XScale, Yscale, nAngle: Extended): Extended;
var
x, y, ang: Extended;
begin
ang := seangle + Angle; // 角度 楕円の角度と開始終了角加算
x := cos(ang) * XScale; // 変倍X位置 長さを1としてX位置計算
y := sin(ang) * YScale; // 変倍Y位置 長さを1としてY位置計算
result := arctan2(y, x) - nAngle; // XYの位置から角度を計算し変倍後の楕円の角度を減算
if result < 0 then result := result + 2 * pi;
if result > 2 * pi then result := result - 2 * pi;
end;
//----------------------------------------------------------------
// 楕円の変倍ルーチン
// 参照 http://marupeke296.com/COL_2D_No7_EllipseVsEllipse.html
// 衝突ルーチンの中の変倍部分を利用して作成しました。
// 楕円 Ellipse 横倍率 XScale 縦倍率 YScale 戻り値 楕円
//----------------------------------------------------------------
function TForm1.Ellipse_magnification(Ellipse: TELLIPSE; XScale, YScale: Extended): TELLIPSE;
var
nx, ny, px, py, ox, oy: Extended;
rx_pow2, ry_pow2: Extended;
A, B, C, D, E, F: Extended;
hk, h, k, th: Extended;
CosTh, SinTh, A_tt, B_tt: Extended;
KK, Rx_tt, Ry_tt: Extended;
begin
// XY スケール値に対する楕円変換係数設定
nx := 1 / XScale * cos(Ellipse.fAngle);
ny := 1 / XScale * sin(Ellipse.fAngle);
px := 1 / YScale * sin(Ellipse.fAngle);
py := 1 / YScale * cos(Ellipse.fAngle);
ox := cos(Ellipse.fAngle) * (- Ellipse.fCx) + sin(Ellipse.fAngle) * (- Ellipse.fCy);
oy := cos(Ellipse.fAngle) * (- Ellipse.fCy) - sin(Ellipse.fAngle) * (- Ellipse.fCx);
// 一般式 Ax^2 + By^2 + Cxy + Dx + Ey + F
rx_pow2 := 1 / (Ellipse.fRad_X * Ellipse.fRad_X);
ry_pow2 := 1 / (Ellipse.fRad_Y * Ellipse.fRad_Y);
A := rx_pow2 * nx * nx + ry_pow2 * ny * ny;
B := rx_pow2 * px * px + ry_pow2 * py * py;
C := 2 * rx_pow2 * nx * px - 2 * ry_pow2 * ny * py;
D := 2 * rx_pow2 * nx * ox - 2 * ry_pow2 * ny * oy;
E := 2 * rx_pow2 * px * ox + 2 * ry_pow2 * py * oy;
F := (ox * ox * rx_pow2) + (oy * oy * ry_pow2) - 1;
// 楕円をゼロ度にする回転角度、原点に移動する移動量の計算
hk := 1 / (C * C - 4 * A * B);
h := (E * C - 2 * D * B) * hk; // X方向移動量
k := (D * C - 2 * A * E) * hk; // Y方向移動量
th := arctan2(C, B - A) / 2; // 回転角度
// 楕円の長径と短径計算
CosTh := cos(Th);
SinTh := sin(Th);
A_tt := A * CosTh * CosTh + B * SinTh * SinTh - C * CosTh * SinTh;
B_tt := A * SinTh * SinTh + B * CosTh * CosTh + C * CosTh * SinTh;
KK := - A * h * h - B * k * k - C * h * k + D * h + E * k - F;
if KK < 0 then KK := 0; // ルートの中の負数防止
Rx_tt := sqrt(KK / A_tt); // 半径a
Ry_tt := sqrt(KK / B_tt); // 半径b
// 開始角の計算
result.startAngle := Start_End_Angle(Ellipse.startAngle, Ellipse.fAngle, XScale, Yscale, -th);
// 終了角の計算
result.endAngle := Start_End_Angle(Ellipse.endAngle, Ellipse.fAngle, XScale, Yscale, -th);
result.fRad_X := Rx_tt;
result.fRad_Y := Ry_tt;
result.fAngle := -th; // 移動量なので符号を反転して位置に変更
result.fCx := -h;
result.fcy := -k;
end;
//------------------------------------------------
// 楕円弧上に交点があるかどうかの判定を行います
// Ellipse1 Ellipse2 楕円
// X 交点座標 X
// Y 交点座標 Y
//------------------------------------------------
function TForm1.intersection_judge(Ellipse1, Ellipse2: TEllipse; X, Y: Extended): boolean;
var
qxy : Extended;
endang : Extended;
begin
Result := False;
// 楕円弧1に対する交点の位置の角度計算
qxy := arctan2((y - Ellipse1.fcy),(x - Ellipse1.fCx)) / pi * 180 - Ellipse1.fAngle;
qxy := angle_amendment(qxy);
endang := Ellipse1.endAngle;
if Ellipse1.startAngle > Ellipse1.endAngle then begin
endang := Ellipse1.endAngle + 360;
if qxy < Ellipse1.startAngle then qxy := qxy + 360;
end;
// 楕円弧1の弧上に交点があるか判定
if (qxy >= Ellipse1.startAngle) and (qxy <= endang) or
(Ellipse1.startAngle = Ellipse1.endAngle) then else exit;
// 楕円弧2に対する交点の位置の角度計算
qxy := arctan2((y - Ellipse2.fcy),(x - Ellipse2.fCx)) / pi * 180 - Ellipse2.fAngle;
qxy := angle_amendment(qxy);
endang := Ellipse2.endAngle;
if Ellipse2.startAngle > Ellipse2.endAngle then begin
endang := Ellipse2.endAngle + 360;
if qxy < Ellipse2.startAngle then qxy := qxy + 360;
end;
// 楕円弧2の弧上に交点があるか判定
if (qxy >= Ellipse2.startAngle) and (qxy < endang) or
(Ellipse2.startAngle = Ellipse2.endAngle) then Result := True
else Result := False;
end;
//-------------------------------------------------------------------
// ar1 円半径
// xbc, ybc 楕円中心位置 xo , yo
// ar, br 楕円半径 a , b
// qbc 楕円角度 qb rad 単位
// q 角度位置 q rad 単位
// x, y 確度q時の楕円上の座標
// x = a * cos(q) * cos(qb) - br * sin(q) * sin(qb) + xo; 座標 x
// y = a * cos(q) * sin(qb) + br * sin(q) * cos(qb) + yo; 座標 y
//-------------------------------------------------------------------
function TForm1.EllipseCircleDistance(ar1, xbc, ybc, ar, br, qbc, q: Extended; var X, Y: Extended): Extended;
var
dis0 : Extended;
cosq, sinq, cosqbc, sinqbc: Extended;
arc, brs : Extended;
begin
cosq := cos(q);
sinq := sin(q);
cosqbc := cos(qbc);
sinqbc := sin(qbc);
arc := ar * cosq;
brs := br * sinq;
X := arc * cosqbc - brs * sinqbc + xbc; // 座標 x
Y := arc * sinqbc + brs * cosqbc + ybc; // 座標 y
dis0 := sqrt(X * X + Y * Y); // 距離計算
result := dis0 - ar1; // 差分 精度 1E-16程度が限度
end;
//------------------------------------
// 二つの楕円の交点計算
//------------------------------------
procedure TForm1.cross_calc;
const
pix2 = 2 * pi;
pis180 = pi / 180;
minok = 1E-14; // 判定係数 1E-14
minnx = 1E-18; // 1E-18程度が ケチ落ちの限度らしい
// 桁落ちがあっても解はでます
bysu = 10000;
var
xans : array[1..4] of Extended;
yans : array[1..4] of Extended;
qb2, qbs : Extended;
xbs : Extended;
ybs : Extended;
rb, qr : Extended;
hsc : Extended;
qbc : Extended;
dis0, dis1, dis2, dis3 : Extended;
qc, q, dq, q1r : Extended;
qback, defq : Extended;
x, y : Extended;
xb, yb : Extended;
chf : byte;
rr1, rq1, rq11 : Extended;
maxlq : Extended;
addf : integer;
ansf : byte;
j, k : integer;
def0, def1 : Extended;
signa : Extended;
okf : boolean;
loopc : cardinal;
calcsc, maxR : Extended;
ac1 : Extended;
xc2, yc2, ac2, bc2 : Extended;
cha : Longint;
EllipseX, EllipseN : TEllipse;
begin
EllipseX.startAngle := 0;
EllipseX.endAngle := 360;
EllipseN.startAngle := 0;
EllipseN.endAngle := 360;
// 座標変換
// 楕円1を原点移動 角度をゼロにします。
// それによって楕円2も相対位置へ移動と回転を行います。
// 楕円位置は原点座標(0,0)なので変数はありません。
cha := round(Ellipse1.fAngle * bysu); // 角度1万分の1以下を丸めます
Ellipse1.fAngle := cha / bysu;
cha := round(Ellipse2.fAngle * bysu);
Ellipse2.fAngle := cha / bysu;
qb2 := Ellipse2.fAngle - Ellipse1.fAngle; // 楕円同志の角度差deg単位
if qb2 < 0 then qb2 := qb2 + 360; // 楕円1の角度をゼロにするので
if qb2 >= 360 then qb2 := qb2 - 360; // 角度差が新しい楕円2の角度になります。
xbs := Ellipse2.fCx - Ellipse1.fCx; // x位置の差 楕円1は原点 X=0
ybs := Ellipse2.fcy - Ellipse1.fcy; // y位置の差 楕円1は原点 y=0
qr := arctan2(ybs, xbs); // 楕円2の位置の角度
rb := sqrt(xbs * xbs + ybs * ybs); // 楕円1と楕円2の距離
q1r := Ellipse1.fAngle / 180 * pi; // 楕円1の角度rad
qbs := qr - q1r; // 楕円2の位置の新角角
if qbs < 0 then qbs := qbs + pix2;
if qbs >= pix2 then qbs := qbs - pix2;
EllipseX.fCx := rb * cos(qbs); // 楕円2の 新X位置
EllipseX.fcy := rb * sin(qbs); // 楕円2の 新y位置
EllipseX.fRad_X := Ellipse2.fRad_X;
EllipseX.fRad_Y := Ellipse2.fRad_Y;
EllipseX.fAngle := qb2 / 180 * pi;
hsc := Ellipse1.fRad_X / Ellipse1.fRad_Y; // 楕円1の縦横比
// 楕円Xの縦横変倍 楕円1側はfRad_Xの円に相当するようにします
EllipseN := Ellipse_magnification(EllipseX, 1, hsc);
maxR := max(Ellipse1.fRad_X, Ellipse1.fRad_Y); // 楕円の最大半径検索
maxlq := max(Ellipse2.fRad_X, Ellipse2.fRad_Y);
maxR := max(maxR, maxlq);
calcsc := 100 / maxR; // 計算倍率係数
repeat
if qb2 >= 180 then qb2 := qb2 - 180;
if qb2 < 0 then qb2 := qb2 + 180;
until (qb2 < 180) and (qb2 >= 0);
if (abs(qb2 - 90) < 1E-4) then begin
if (abs(Ellipse1.fCx * calcsc - Ellipse2.fCx * calcsc) < 1E-6) and
(abs(Ellipse1.fCy * calcsc - Ellipse2.fCy * calcsc) < 1E-6) and
(abs(Ellipse1.fRad_X * calcsc - Ellipse2.fRad_Y * calcsc) < 1E-7) and
(abs(Ellipse1.fRad_Y * calcsc - Ellipse2.fRad_X * calcsc) < 1E-7) then begin
application.MessageBox('楕円の値が殆ど同じです','楕円の値',0);
exit;
end;
end;
if qb2 > 90 then qb2 := 180 - qb2;
if (qb2 < 1E-4) then begin
if (abs(Ellipse1.fCx * calcsc - Ellipse2.fCx * calcsc) < 1E-6) and
(abs(Ellipse1.fCy * calcsc - Ellipse2.fCy * calcsc) < 1E-6) and
(abs(Ellipse1.fRad_X * calcsc - Ellipse2.fRad_X * calcsc) < 1E-7) and
(abs(Ellipse1.fRad_Y * calcsc - Ellipse2.fRad_Y * calcsc) < 1E-7) then begin
application.MessageBox('楕円の値が殆ど同じです','楕円の値',0);
exit;
end;
end;
// 交点の計算をいつも同じ値で計算
ac1 := Ellipse1.fRad_X * calcsc; // するための補正です
xc2 := EllipseN.fCx * calcsc; // 大きい方の楕円の長径を100にします。
yc2 := EllipseN.fcy * calcsc; // 他の値は、100に相対する値になります。
ac2 := EllipseN.fRad_X * calcsc;
bc2 := EllipseN.fRad_Y * calcsc;
qbc := EllipseN.fAngle; // 楕円N角度rad単位
// 一番遠い位置の検索 一回転検索
q := 0; // 最初の角度
dq := pis180; // Δq = 1度
dis1 := EllipseCircleDistance(ac1, xc2, yc2, ac2, bc2, qbc, q, x, y);
maxlq := 0;
xb := x;
yb := y;
repeat
q := q + dq; // Δq角度加算
// 半径ar1の円の中心のから楕円状の位置の距離から円の半径を差し引いた値計算 戻り値
dis0 := EllipseCircleDistance(
ac1, // 楕円1の半径a
xc2, // 楕円2の中心x
yc2, // 楕円2の中心y
ac2, // 楕円2の半径a
bc2, // 楕円2の半径b
qbc, // 楕円2のの角度
q, // 楕円状の座標計算用角度
x, // 楕円2上のx座標
y // 楕円2上のy座標
);
if abs(dis1) < abs(dis0) then begin // 大きいほうの値を保存
dis1 := dis0;
maxlq := q;
xb := x;
yb := y;
end;
until q > pix2; // 一周したら終了
xb := xb / calcsc; // スケール戻し
yb := yb / calcsc;
yb := yb / hsc; // y座標戻し
rr1 := sqrt(xb * xb + yb * yb); // 原点からの距離
rq1 := arctan2(yb, xb); // 角度
rq11 := rq1 + q1r; // 元の角度に戻す
x := rr1 * cos(rq11) + Ellipse1.fCx; // x座標計算
y := rr1 * sin(rq11) + Ellipse1.fcy; // y座標計算
// 交点検索開始点の表示
EllipseEx(image1.Canvas,
image1.Height, // canvas高さ
3, // 線種
2, // 線幅
clred, // 色
3, // 半径a
3, // 半径b
x * magnification - shift_x, // 中心位置x
y * magnification - shift_y, // 中心位置y
0, // 回転角 deg
0, // 作図開始角
360); // 作図終了角
// 楕円1と楕円2交点検索 円でも可能です
ansf := 0; // 答えの数クリア
qc := 0; // 一周チェック用リセット
q := maxlq; // 検索スタート位置セット
dis2 := 0;
dis3 := 0;
for k := 1 to 4 do begin
dq := pis180; // Δq = 1度
chf := 1; // 計算チェックフラグ
dis1 := EllipseCircleDistance(ac1, xc2, yc2, ac2, bc2, qbc, q, x, y); // 最初の差分値計算
addf := 0; // 計算回数クリア
okf := false; // 計算確定フラグリセット
loopc := 0; // ループカウンタークリア
if qc < pix2 then // 一周していなかったら
repeat
qback := q;
q := q + dq; // 計算角度加算
defq := q - qback;
if q > pix2 then q := q - pix2; // 360度を越えたら360度以下に
qc := qc + dq; // 一周確認用角度加算
inc(addf); // 加算回数インクリメント
dis0 := EllipseCircleDistance(ac1, xc2, yc2, ac2, bc2, qbc, q, x, y); // 差分値計算
signa := dis1 * dis0; // データーの符号が変わったかの判定値計算
if signa < 0 then begin // 差分計算結果の符号が変わったら
q := q - dq; // 角度を一つ前に戻します
qc := qc - dq;
dq := dq / 2; // Δq の値を二分の一にします
dis0 := dis1; // データーのバックアップも一つ戻し
dis1 := dis2;
dec(addf); // 加算フラグ戻し
end;
def0 := abs(dis0); // 差分データーの絶対値
def1 := abs(dis1);
if def0 < def1 then chf := 2; // データーが小さくなったら計算フラグ2
if (chf = 2) and (addf > 2) then // 計算フラグ 2 で 2回以上計算されていたら
if def0 > def1 then begin
q := q - dq - dq; // 角度を二回分もどします
qc := qc - dq - dq;
dq := dq / 2; // Δq の値を二分の一にします
dis0 := dis2;
dis1 := dis3; // データーのバックアップも二つ戻し
dec(addf, 2); // 加算フラグ戻し
end;
if (def0 < minok) then begin // 差分値の絶対値が指定値以下になったら
chf := 0; // 答え y
inc(ansf); // 答えの数インクリメント
okf := true; // データーが確定したフラグセット
end
else begin // 指定値以下でなかったら
if (defq = 0) or (dq < minnx) then begin // Δq の値を確認 十分に小さい場合近づいただけで交点無し
// defq = 0 は Δq 加算しても値が変われない場合
if qc <= pix2 then begin // 一周計算していなかったら
dq := pis180; // Δq = 1度
addf := 0; // 計算の数リセット
chf := 3; // ピークを超えたフラグセット
end;
end;
end;
if qc > pix2 then chf := 0; // 一周したら終了フラグセット
dis3 := dis2; // データーのバックアップ
dis2 := dis1;
dis1 := dis0;
inc(loopc); // ループカウンターインクリメント
if loopc > 2000 then chf := 0; // 収束しなかった時ループ回数で終了します
until chf = 0;
if okf then begin
y := y / calcsc; // スケール戻し
x := x / calcsc;
y := y / hsc; // yの値楕円1半径補正戻し
rr1 := sqrt(x * x + y * y); // 原点からの距離
rq1 := arctan2(y, x); // 角度
rq11 := rq1 + q1r; // 元の角度に戻す
xans[ansf] := rr1 * cos(rq11) + Ellipse1.fCx; // x座標計算
yans[ansf] := rr1 * sin(rq11) + Ellipse1.fcy; // y座標計算
end;
qc := qc + dq * 8; // 次の検索のため角度を進めます
q := q + dq * 8; // 進めないとΔq分交点の手前の事があります
end; // 桁落ち限度までΔqが小さくなるので少し多めに加算します。
// 交点位置作図と表示
if ansf > 0 then
for j := 1 to ansf do begin
// 円弧上に交点があるかどうか判定して交点有ったら作図します
if intersection_judge(Ellipse1, Ellipse2, xans[j], yans[j]) then begin // 交点の有無判定
// 交点〇作図
EllipseEx(image1.Canvas,
image1.Height, // canvas高さ
3, // 線種
2, // 線幅
clBlue, // 色
4, // 半径a
4, // 半径b
xans[j] * magnification - shift_x, // 中心位置x
yans[j] * magnification - shift_y, // 中心位置y
0, // 回転角 deg
0, // 作図開始角
360); // 作図終了角
image1.Canvas.TextOut( 30, j * 18, 'X' + intTostr(j) + '=' + floatTostrF(xans[j], ffFixed, 12, 6));
image1.Canvas.TextOut(200, j * 18, 'Y' + intTostr(j) + '=' + floatTostrF(yans[j], ffFixed, 12, 6));
end;
end;
end;
//--------------------------------------------------------
// 入力された楕円の描画
// 楕円作図のy方向は、楕円作図ルーチンで修正されます。
//--------------------------------------------------------
procedure TForm1.inputdata_drawing;
var
left_min, left_max : Extended;
top_min, top_max : Extended;
all_width, all_height: Extended;
ac1, ac2 : Extended;
// 楕円作図 線種 線幅 色指定
procedure EllipseDraw(Ellipse : TEllipse; linetype, thickness: integer; color: Tcolor);
var
tmp : Extended;
begin
// 破線は開始角と終了角入れ替え
if linetype = 0 then begin
tmp := Ellipse.startAngle;
Ellipse.startAngle := Ellipse.endAngle;
Ellipse.endAngle := tmp;
end;
// 楕円作図
EllipseEx(image1.Canvas,
image1.Height, // canvas高さ
linetype, // 線種 実践
thickness, // 線幅
color, // 色
Ellipse.fRad_X * magnification, // 半径a
Ellipse.fRad_Y * magnification, // 半径b
Ellipse.fCx * magnification - shift_x, // 中心位置x
Ellipse.fcy * magnification - shift_y, // 中心位置y
Ellipse.fAngle, // 回転角 deg
Ellipse.startAngle, // 作図開始角
Ellipse.endAngle); // 作図終了角
end;
begin
// 最大半径検索
ac1 := Ellipse1.fRad_X;
if Ellipse1.fRad_X < Ellipse1.fRad_Y then begin
ac1 := Ellipse1.fRad_Y;
end;
ac2 := Ellipse2.fRad_X;
if Ellipse2.fRad_X < Ellipse2.fRad_Y then begin
ac2 := Ellipse2.fRad_Y;
end;
// 画像の表示調整 image1の範囲に入るように調整します。
// 左右最大値
left_min := Ellipse1.fCx - ac1;
if Ellipse2.fCx - ac2 < left_min then left_min := Ellipse2.fCx - ac2;
// 左右最大値
left_max := Ellipse1.fCx + ac1;
if Ellipse2.fCx + ac2 > left_max then left_max := Ellipse2.fCx + ac2;
// 最大幅
all_width := left_max - left_min;
// 上下最小値
top_min := Ellipse1.fcy - ac1;
if Ellipse2.fcy - ac2 < top_min then top_min := Ellipse2.fcy - ac2;
// 上下最大値
top_max := Ellipse1.fcy + ac1;
if Ellipse2.fcy + ac2 > top_max then top_max := Ellipse2.fcy + ac2;
// 最大高
all_height := top_max - top_min;
// 高さ倍率
top_max := (image1.Height - draw_margin * 2) / all_Height;
// 幅倍率
magnification := (image1.Width - draw_margin * 2) / all_width;
// 倍率の大きい方の選択
if magnification > top_max then magnification := top_max;
// 表示シフト量
shift_x := left_min * magnification - draw_margin;
shift_y := top_min * magnification - draw_margin;
// イメージクリア
imageClear;
// 楕円1作図 線種 線幅 色
EllipseDraw(Ellipse1, 3, 1, clRed);
EllipseDraw(Ellipse1, 0, 1, clRed);
// 楕円2作図 線種 線幅 色
EllipseDraw(Ellipse2, 3, 1, clBlue);
EllipseDraw(Ellipse2, 0, 1, clBlue);
end;
// 角度の範囲0から360の範囲に調整
function TForm1.angle_amendment(angle : Extended): Extended;
begin
repeat
if angle >= 360 then angle := angle - 360;
until angle < 360;
repeat
if angle < 0 then angle := angle + 360;
until angle >= 0;
Result := angle;
end;
// データー入力処理
procedure TForm1.SelectBtnClick(Sender: TObject);
var
ch: integer;
begin
// 楕円1のデーター
val(radius_a1_Edit.Text, Ellipse1.fRad_X, ch);
if ch <> 0 then begin
application.MessageBox('楕円1の半径a1数値ではありません', '楕円1の半径a1', 0);
exit;
end;
if Ellipse1.fRad_X <= 0 then begin
application.MessageBox('楕円1の半径a1が0か0以下です', '楕円1の半径a1', 0);
exit;
end;
val(radius_b1_Edit.Text, Ellipse1.fRad_Y, ch);
if ch <> 0 then begin
application.MessageBox('楕円1の半径b1数値ではありません', '楕円1の半径b1', 0);
exit;
end;
if Ellipse1.fRad_Y <= 0 then begin
application.MessageBox('楕円1の半径b1が0か0以下です', '楕円1の半径b1', 0);
exit;
end;
val(Center_x1_Edit.Text, Ellipse1.fCx, ch);
if ch <> 0 then begin
application.MessageBox('楕円1の中心位置x1数値ではありません', '楕円1の中心位置x1', 0);
exit;
end;
val(Center_y1_Edit.Text, Ellipse1.fcy, ch);
if ch <> 0 then begin
application.MessageBox('楕円1の中心位置y1数値ではありません', '楕円1の中心位置y1', 0);
exit;
end;
val(angle_q1_Edit.Text, Ellipse1.fAngle, ch);
if ch <> 0 then begin
application.MessageBox('楕円1の角度θ1数値ではありません', '楕円1の角度θ1', 0);
exit;
end;
val(Start_angle_S1.Text, Ellipse1.startAngle, ch);
if ch <> 0 then begin
application.MessageBox('楕円1の開始角数値ではありません', '楕円1の開始角S1', 0);
exit;
end;
val(End_angle_E1.Text, Ellipse1.endAngle, ch);
if ch <> 0 then begin
application.MessageBox('楕円1の終了角数値ではありません', '楕円1の終了角E1', 0);
exit;
end;
// 楕円2のデーター
val(radius_a2_Edit.Text, Ellipse2.fRad_X, ch);
if ch <> 0 then begin
application.MessageBox('楕円2の半径a2数値ではありません', '楕円2の半径a2', 0);
exit;
end;
if Ellipse2.fRad_X <= 0 then begin
application.MessageBox('楕円2の半径a2が0か0以下です', '楕円2の半径a2', 0);
exit;
end;
val(radius_b2_Edit.Text, Ellipse2.fRad_Y, ch);
if ch <> 0 then begin
application.MessageBox('楕円2の半径b2数値ではありません', '楕円2の半径b2', 0);
exit;
end;
if Ellipse2.fRad_Y <= 0 then begin
application.MessageBox('楕円2の半径b2が0か0以下です', '楕円2の半径b2', 0);
exit;
end;
val(Center_x2_Edit.Text, Ellipse2.fCx, ch);
if ch <> 0 then begin
application.MessageBox('楕円2の中心位置x2数値ではありません', '楕円2の中心位置x2', 0);
exit;
end;
val(Center_y2_Edit.Text, Ellipse2.fcy, ch);
if ch <> 0 then begin
application.MessageBox('楕円2の中心位置y2数値ではありません', '楕円2の中心位置y2', 0);
exit;
end;
val(angle_q2_Edit.Text, Ellipse2.fAngle, ch);
if ch <> 0 then begin
application.MessageBox('楕円2の角度θ2数値ではありません', '楕円2の角度θ2', 0);
exit;
end;
val(Start_angle_S2.Text, Ellipse2.startAngle, ch);
if ch <> 0 then begin
application.MessageBox('楕円2の開始角数値ではありません', '楕円2の開始角S2', 0);
exit;
end;
val(End_angle_E2.Text, Ellipse2.endAngle, ch);
if ch <> 0 then begin
application.MessageBox('楕円2の終了角数値ではありません', '楕円2の終了角E2', 0);
exit;
end;
// 入力された楕円角度の値修正 0 ~ 360 の範囲に入る様にします。
Ellipse1.fAngle := angle_amendment(Ellipse1.fAngle);
Ellipse2.fAngle := angle_amendment(Ellipse2.fAngle);
Ellipse1.startAngle := angle_amendment(Ellipse1.startAngle);
Ellipse1.endAngle := angle_amendment(Ellipse1.endAngle);
Ellipse2.startAngle := angle_amendment(Ellipse2.startAngle);
Ellipse2.endAngle := angle_amendment(Ellipse2.endAngle);
inputdata_drawing;
cross_calc;
end;
procedure TForm1.FormCreate(Sender: TObject);
begin
// 線種配列确保
setlength(LPitch, LineN);
// 線種データーセット
LPitch[0].segment := 2; // 破線
LPitch[0].Pitch[0] := 6;
LPitch[0].Pitch[1] := 3;
LPitch[1].segment := 4; // 1点鎖線
LPitch[1].Pitch[0] := 15;
LPitch[1].Pitch[1] := 3;
LPitch[1].Pitch[2] := 3;
LPitch[1].Pitch[3] := 3;
LPitch[2].segment := 6; // 2点鎖線
LPitch[2].Pitch[0] := 18;
LPitch[2].Pitch[1] := 3;
LPitch[2].Pitch[2] := 3;
LPitch[2].Pitch[3] := 3;
LPitch[2].Pitch[4] := 3;
LPitch[2].Pitch[5] := 3;
// イメージクリア
imageClear;
image1.Canvas.Font.Name := 'MS ゴシック';
// image1.Canvas.Font.Style := [fsbold];
image1.Canvas.Font.Height := 13;
end;
Initialization
Ellipse2.startAngle := 0;
Ellipse2.endAngle := 360;
Ellipse1.startAngle := 0;
Ellipse1.endAngle := 360;
end.
 EllipsesNodeD.zip
EllipsesNodeD.zip
各種プログラム計算例に戻る
最初に戻る

