2018/07/18
楕円積分の配列確保時64ビットモードで正しく確保できないのを修正しました。
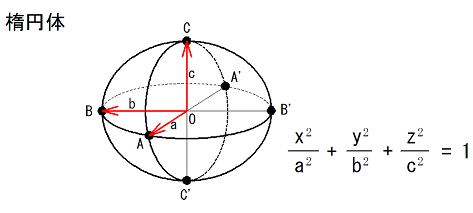
楕円体の表面積(2)
楕円体の表面積(1)で、分割積分を取り上げましたが、此処では、楕円体の第一種不完全積分と第二種不完全積分をもちいたプログラムを紹介します。

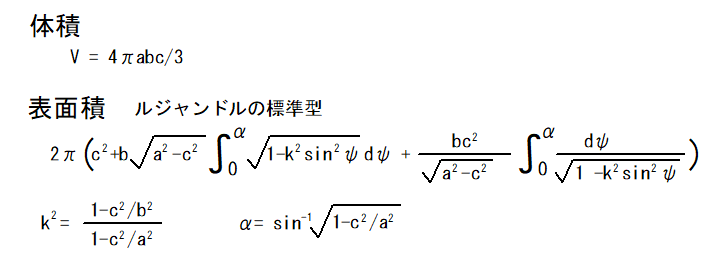
楕円体の表面積(1)の分割積分では、ヤコービの標準型でプログラムを作成しましたが、此処では、ルジャンドルの標準型を使用します。
上図には2つの積分の計算があり、最初が第2種不完全積分で、次のが第1種不完全積分です。
この不完全積分は、ランデン変換 をもちいて計算しますが、計算方法は、インターネットで、”楕円体の不完全積分”,”第一種不完全積分”,”第二種不完全積分”で検索すると沢山検索されます。
上の計算式からわかる通り、a=c, b=c の場合、計算出来ないことが分かります。
計算の条件は、a≧b>c となります。
等しい値が存在する場合は、次のようにして判別して、それぞれの計算式で、計算します。

楕円体の三個の値を大きい順にソートした場合左図の様になった場合は、回転楕円体、球として計算します。
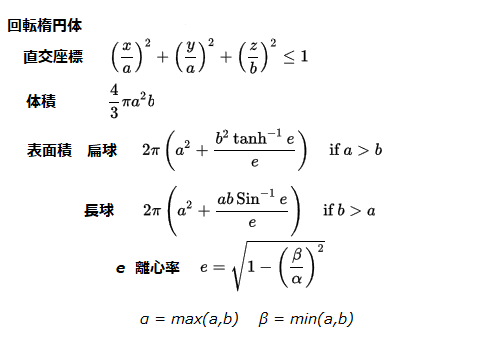
回転楕円体、球の場合、表面積の計算は、一般式で計算が可能です。
楕円体として入力された値のうち、等しい値を a とし 、等しくない値を b として、左の計算式に当てはめて計算すれば、回転楕円体の表面積として計算されます。

3個の値が等しい場合は、球なので簡単に表面積が計算されます。
プログラム
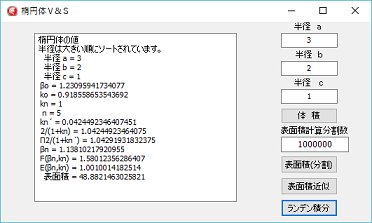
プログラムは、分割積分と、ランデン変換積分の表面積計算を作成してみました。
分割計算に対して、ランデン変換の場合、圧倒的に計算回数が少ないので、一瞬にして計算が終了します。
a=b>c
の場合、ランデン変換による計算でも可能ですが、回転楕円体として計算しています。
ランデン変換による場合、此処のプログラムでは、a=b>c の場合、kn' kndの配列が確保されないので注意が必要です。
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls, math;
type
TForm1 = class(TForm)
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
LabeledEdit3: TLabeledEdit;
Button1: TButton;
Button2: TButton;
Memo1: TMemo;
Button3: TButton;
Button4: TButton;
LabeledEdit4: TLabeledEdit;
procedure Button1Click(Sender: TObject);
procedure Button2Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure Button3Click(Sender: TObject);
procedure Button4Click(Sender: TObject);
private
{ Private 宣言 }
function datain: boolean;
procedure Spheroid;
procedure ball;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
var
a, b, c : double;
// スワップ
procedure maxswap(var a, b: double);
var
tmp: double;
begin
if a < b then begin
tmp := a;
a := b;
b := tmp;
end;
end;
// 入力処理
function TForm1.datain: boolean;
var
ch , I : integer;
din: array[0..2] of double;
begin
result := False;
val(LabeledEdit1.text, din[0], ch);
if ch <> 0 then begin
application.MessageBox('半径aに間違いがあります。','注意', 0);
exit;
end;
val(LabeledEdit2.text, din[1], ch);
if ch <> 0 then begin
application.MessageBox('半径bに間違いがあります。','注意', 0);
exit;
end;
val(LabeledEdit3.text, din[2], ch);
if ch <> 0 then begin
application.MessageBox('半径cに間違いがあります。','注意', 0);
exit;
end;
if din[0] <= 0 then begin
application.MessageBox('半径aに間違いがあります。','注意', 0);
exit;
end;
if din[1] <= 0 then begin
application.MessageBox('半径bに間違いがあります。','注意', 0);
exit;
end;
if din[2] <= 0 then begin
application.MessageBox('半径cに間違いがあります。','注意', 0);
exit;
end;
// ソート
for I := 0 to 2 do
for ch := 0 to 1 do
maxswap(din[ch], din[ch + 1]);
a := din[0];
b := din[1];
c := din[2];
memo1.Clear;
memo1.Lines.Append('楕円体の値');
memo1.Lines.Append('半径は大きい順にソートされています。');
memo1.Lines.Append(' 半径 a = ' + floatTostr(a));
memo1.Lines.Append(' 半径 b = ' + floatTostr(b));
memo1.Lines.Append(' 半径 c = ' + floatTostr(c));
result := True;
end;
// 初期設定
procedure TForm1.FormCreate(Sender: TObject);
begin
top := (screen.Height - height) div 2;
left := (screen.Width - width) div 2;
memo1.Clear;
end;
// 体積計算
procedure TForm1.Button1Click(Sender: TObject);
var
v : double;
begin
if not datain then exit;
v := 4 * pi * a * b * c / 3;
memo1.Lines.Append(' 体積 = ' + floatTostr(v));
end;
// 球の表面積
procedure TForm1.ball;
var
s : double;
begin
s := 4 * pi * a * a;
memo1.Lines.Append('球(積分計算無し)');
memo1.Lines.Append(' 表面積 = ' + floatTostr(s));
end;
// 表面積計算 ルジャンドルの標準形
procedure TForm1.Button2Click(Sender: TObject);
var
kim : integer; // kim = 10000000 分割数 doubleでの限界値 桁落ち限界
I : integer;
kp2, alpha : double;
dps, sp2 : double;
pinteg, sinteg : double;
sq1sp : double;
sqa2mc2 : double;
sq1b : double;
s : double;
begin
if not datain then exit;
val(LabeledEdit4.text, kim, I);
if I <> 0 then begin
application.MessageBox('分割数に間違いがあります。','注意', 0);
exit;
end;
// c = a の場合球の計算
if c = a then begin // a = c ならば a = b = c
ball; // 球の表面積
exit;
end;
kp2 := (1 - c * c / b / b) / ( 1 - c * c / a / a); // k^2
alpha := arcsin(sqrt(1 - c * c / a / a)); // α
dps := alpha / kim; // dΨ
pinteg := 0;
sinteg := 0;
sq1b := dps / 2; // 中間値
for I := 1 to kim do begin
sp2 := sin(dps * I - sq1b); // 分割中間点の値
sp2 := sp2 * sp2;
sq1sp := sqrt(1 - kp2 * sp2); // 分割中間位置の値計算
pinteg := pinteg + sq1sp; // 加算
sinteg := sinteg + 1 / sq1sp; // 逆数加算
end;
pinteg := pinteg * dps; // 分割値を乗算
sinteg := sinteg * dps; // 分割値を乗算
sqa2mc2 := sqrt(a * a - c * c);
s := c * c + b * sqa2mc2 * pinteg + b * c * c / sqa2mc2 * sinteg;
s := s * 2 * pi;
memo1.Lines.Append(' 表面積 = ' + floatTostr(s));
end;
// 表面積近似計算
procedure TForm1.Button3Click(Sender: TObject);
const
P = 1.6075;
var
s : double;
ip : double;
begin
if not datain then exit;
ip := 1 / p;
s := power(a, p) * power(b, p)
+ power(a, p) * power(c, P)
+ power(b, p) * power(c, p);
s := s / 3;
s := power(s, ip);
s := s * 4 * pi;
memo1.Lines.Append(' 表面積近似 = ' + floatTostr(s));
end;
// 回転楕円体
procedure TForm1.Spheroid;
var
alpha, beta : double;
e : double;
s : double;
begin
// a が2個 bが1個の回転楕円体に変換
if (a = b) and (b <> c) then b := c
else
if (a <> b) and (b = c) then begin
b := a;
a := c;
end;
alpha := max(a, b);
beta := min(a, b);
// 離心率
e := sqrt(1 - beta * beta / alpha / alpha);
// 表面積
if a > b then
// 扁球
s := 2 * pi * (a * a + b * b * arctanh(e) / e)
else
// 長球
s := 2 * pi * (a * a + a * b * arcsin(e) / e);
memo1.Lines.Append('回転楕円体(積分計算無し)');
memo1.Lines.Append(' 表面積 = ' + floatTostr(s));
end;
// ランデン変換による積分
// http://www1.bbiq.jp/math7557/InComp-2nd-Elliptic-Landen-Caluculate.html
procedure TForm1.Button4Click(Sender: TObject);
var
I : integer;
k0 : double; // ko
n : integer; // n
kn : array of double; // kn
knd : array of double; // kn'
Pkn : array of double; // 2/(1+kn)
Pknd : array of double; // Π2/(1+kn')
beta : array of double; // β(rad)
Lnsc : double; // Ln(x)
Fbkn : array of double; // F(βn,kn)
Ebkn : array of double; // E(βn,kn)
sqa2mc2 : double;
s : double; // 表面積
begin
if not datain then exit;
// 回転楕円体の場合
if ((a = b) and (b <> c)) or ((a <> b) and (b = c)) then begin
Spheroid; // 回転楕円体
exit;
end;
// 球の場合
if (a = c) then begin // a = c ならば a = b = c
ball; // 球の表面積
exit;
end;
// 楕円体
n := 0;
k0 := sqrt((1 - c * c / b / b) / ( 1 - c * c / a / a)); // ko
setlength(kn, n + 1);
Lnsc := 0;
kn[n] := k0;
// kn[n] が 1になるまで繰り返し n(繰り返し数) の値を取得します
// 配列の大きさは n + 1;
while Lnsc <> Kn[n] do begin // 2018/07/18 修正
Lnsc := Kn[n];
inc(n);
setlength(kn, n + 1); // kn
kn[n] := 2 * sqrt(Kn[n - 1])/(1 + Kn[n - 1]);
end;
dec(n);
setlength(kn, n + 1);
setlength(knd, n); // kn'の配列の大きさは n でOk kn'[x] 使用時のxの値に注意します
setlength(pkn, n + 1);
setlength(pknd, n + 1);
setlength(beta, n + 1);
setlength(Fbkn, n + 1);
setlength(Ebkn, n + 1);
// 積分計算
for I := 0 to n - 1 do
knd[I] := (1 - kn[I]) / (1 + Kn[I]);
for I := 0 to n do
pkn[I] := 2 / (1 + kn[I]); // 2/(1+kn)
pknd[n] := pkn[n];
for I := n - 1 downto 0 do
pknd[I] := pknd[I + 1] * pkn[I]; // Π2/(1+kn')
beta[0] := arcsin(sqrt(1 - c * c / a / a)); // βoセット
for I := 1 to n do
beta[I] := (arcsin(kn[I - 1] * sin(beta[I - 1])) + beta[I - 1]) / 2; // β(rad)
Lnsc := ln((1 + sin(beta[n]))/cos(beta[n])); // Ln(x)
for I := 0 to n do
Fbkn[I] := pknd[I] * Lnsc; // F(βn,kn)
Ebkn[n] := sin(beta[n]);
for I := n - 1 downto 0 do
Ebkn[I] := (2 * Ebkn[I + 1] + 2 * knd[I] * Fbkn[I + 1])
/ (1 + Knd[I]) - kn[I] * sin(beta[I]); // E(βn,kn)
sqa2mc2 := sqrt(a * a - c * c);
s := c * c + b * sqa2mc2 * Ebkn[0] + b * c * c / sqa2mc2 * Fbkn[0];
s := s * 2 * pi;
memo1.Lines.Append(' βo = ' + floatTostr(beta[0] / pi * 180) + '°');
memo1.Lines.Append(' βn = ' + floatTostr(beta[n] / pi * 180) + '°');
memo1.Lines.Append(' ko = ' + floatTostr(kn[0]));
memo1.Lines.Append(' kn = ' + floatTostr(kn[n]));
memo1.Lines.Append(' n = ' + intTostr(n + 1));
if n > 0 then memo1.Lines.Append(' kn´ = ' + floatTostr(knd[0])); // a=bの場合n=0 knd配列長さ無し
memo1.Lines.Append(' 2/(1+kn) = ' + floatTostr(pkn[0]));
memo1.Lines.Append(' Π2/(1+kn´) = ' + floatTostr(pknd[0]));
memo1.Lines.Append(' F(βn,kn) = ' + floatTostr(Fbkn[0]));
memo1.Lines.Append(' E(βn,kn) = ' + floatTostr(Ebkn[0]));
memo1.Lines.Append(' 表面積 = ' + floatTostr(s));
end;
end.
![]() ellipsoid0.zip
ellipsoid0.zip
各種プログラム計算例に戻る