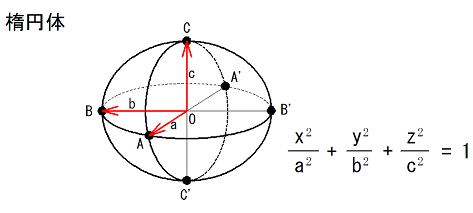
楕円体の表面積(1)
楕円体の表面積の計算について、まず最初に、一般的な分割による積分計算をしてみました。
(後で、楕円体の第1、2種不完全積分による方法のプログラムを検討します)
分割による方法であれば、計算精度は低いですが、プログラムのミスは少ないので、次のプログラムでの値が正しいかどうかの確認にも使用できます。

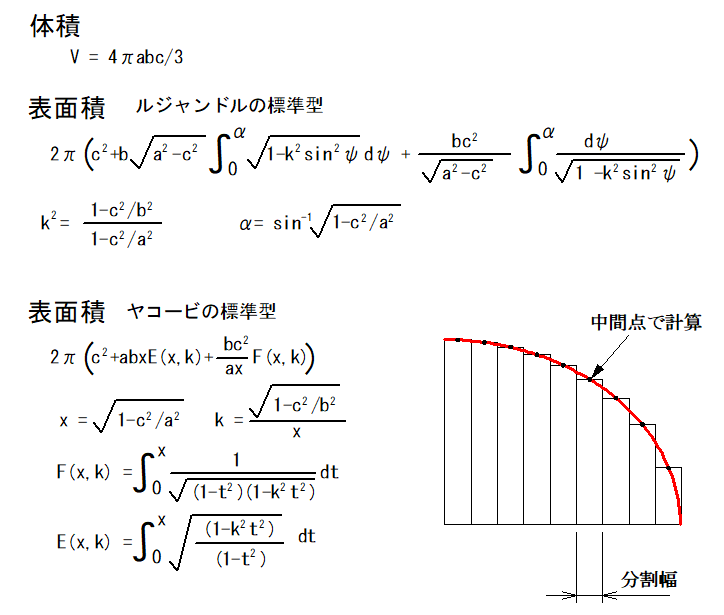
回転楕円体の表面積は、単純な計算で求める事が出来ますが、楕円体の表面積は、楕円体積分を行う必要があります。
此処でのプログラムは、一般的な分割による積分法です。
分割数を多くするほど正確な値となります。
少しでも精度を上げるため、左図のグラフの様に、分割の中間点の値で分割部分の面積を求めています。
ルジャンドルの標準型だと、Sin2Ψの計算があり、計算が遅くなるので、ヤコービの標準型で、まずは、プログラムを作成してみました。
分割数が1000だと、有効桁数三桁、100000だと有効桁数五桁ぐらいで、分割数10N
のNの値程度かそれより多い有効桁数となるようです。
10000000の分割でも、今のPCは1秒程度で計算できます。
Doubleの演算精度だと、10000000分割程度が、精度上の限界の様です。
実際に計算をしてみると、
半径 a = 3
半径 b = 2
半径 c = 1
表面積 = 48.8821463025811
(正解 48.882146302582)
可成り正解に近い値となつています。
実用上は、104程度の分割数で十分かと思います。
表面積 = 48.8821460826706
104であると、計算は一瞬で終了します。
黒字の部分が正解とあっている部分ですが、小数点以下6桁まであっているので実用上問題ないと思われます。
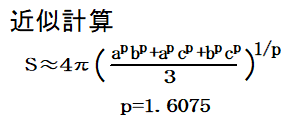
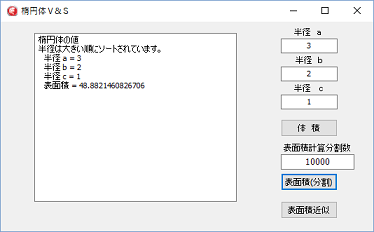
計算上、a>b>c の必要があり、演算エラーを防止する為、入力された値を大きい順にソートしてから計算しています。
a=b=cの時は球となります。
近似計算の場合、簡単に計算出来ますが、精度は、三桁程度です。
この場合は球(a=b=c)の計算もできます、球は正しい答えが得られます。
プログラム
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls, math;
type
TForm1 = class(TForm)
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
LabeledEdit3: TLabeledEdit;
Button1: TButton;
Button2: TButton;
Memo1: TMemo;
Button3: TButton;
LabeledEdit4: TLabeledEdit;
procedure Button1Click(Sender: TObject);
procedure Button2Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure Button3Click(Sender: TObject);
private
{ Private 宣言 }
function datain: boolean;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
var
a, b, c : double;
// スワップ
procedure maxswap(var a, b: double);
var
tmp: double;
begin
if a < b then begin
tmp := a;
a := b;
b := tmp;
end;
end;
// データー入力処理
function TForm1.datain: boolean;
var
ch , I : integer;
din: array[0..2] of double;
begin
result := False;
val(LabeledEdit1.text, din[0], ch);
if ch <> 0 then begin
application.MessageBox('半径aに間違いがあります。','注意', 0);
exit;
end;
val(LabeledEdit2.text, din[1], ch);
if ch <> 0 then begin
application.MessageBox('半径bに間違いがあります。','注意', 0);
exit;
end;
val(LabeledEdit3.text, din[2], ch);
if ch <> 0 then begin
application.MessageBox('半径cに間違いがあります。','注意', 0);
exit;
end;
if din[0] <= 0 then begin
application.MessageBox('半径aに間違いがあります。','注意', 0);
exit;
end;
if din[1] <= 0 then begin
application.MessageBox('半径bに間違いがあります。','注意', 0);
exit;
end;
if din[2] <= 0 then begin
application.MessageBox('半径cに間違いがあります。','注意', 0);
exit;
end;
for I := 0 to 2 do
for ch := 0 to 1 do
maxswap(din[ch], din[ch + 1]);
a := din[0];
b := din[1];
c := din[2];
memo1.Clear;
memo1.Lines.Append('楕円体の値');
memo1.Lines.Append('半径は大きい順にソートされています。');
memo1.Lines.Append(' 半径 a = ' + floatTostr(a));
memo1.Lines.Append(' 半径 b = ' + floatTostr(b));
memo1.Lines.Append(' 半径 c = ' + floatTostr(c));
result := True;
end;
// 初期設定
procedure TForm1.FormCreate(Sender: TObject);
begin
top := (screen.Height - height) div 2;
left := (screen.Width - width) div 2;
memo1.Clear;
end;
// 体積計算
procedure TForm1.Button1Click(Sender: TObject);
var
v : double;
begin
if not datain then exit;
v := 4 * pi * a * b * c / 3;
memo1.Lines.Append(' 体積 = ' + floatTostr(v));
end;
// 表面積計算 ヤコービの標準形使用
procedure TForm1.Button2Click(Sender: TObject);
var
kim : integer; // kim = 10000000; 分割数 doubleでの限界値 桁落ち限界
I : integer;
x, k2 : double;
dt, dts2, t, t2 : double;
omt2, omtk2t2 : double;
s : double;
Fxk, Exk : double;
begin
if not datain then exit;
val(LabeledEdit4.text, kim, I);
if I <> 0 then begin
application.MessageBox('分割数に間違いがあります。','注意', 0);
exit;
end;
if (a = b) and (b = c) then begin
application.MessageBox('球の計算は出来ません。','注意', 0);
exit;
end;
x := sqrt(1 - c * c / a / a);
k2 := (1 - c * c / b / b) / (1 - c * c / a / a);
dt := x / kim; // Δt
dts2 := dt / 2; // 分割中間点
Fxk := 0;
Exk := 0;
for I := 1 to kim do begin
t := I * dt - dts2; // 中間点
t2 := t * t;
omt2 := 1 - t2;
omtk2t2 := 1 - k2 * t2;
Fxk := Fxk + 1 / sqrt(omt2 * omtk2t2); // F(x, k)
Exk := Exk + sqrt(omtk2t2 / omt2); // E(x, k)
end;
Fxk := Fxk * dt; // F(x, k)dt
Exk := Exk * dt; // E(x, k)dt
s := c * c + a * b * x * Exk + b * c * c / a / x * Fxk;
s := s * 2 * pi;
memo1.Lines.Append(' 表面積 = ' + floatTostr(s));
end;
// 表面積近似値計算
procedure TForm1.Button3Click(Sender: TObject);
const
P = 1.6075;
var
s : double;
ip : double;
begin
if not datain then exit;
ip := 1 / P;
s := power(a, P) * power(b, P)
+ power(a, P) * power(c, P)
+ power(b, P) * power(c, P);
s := s / 3;
s := power(s, ip);
s := s * 4 * pi;
memo1.Lines.Append(' 表面積近似 = ' + floatTostr(s));
end;
end.
![]() ellipsoidA.zip
ellipsoidA.zip
各種プログラム計算例に戻る