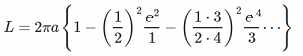
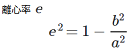
2018/08/20
ランデン変換 while 分収束判定変更(無限ループの可能性回避)
2018/04/15
∑√(1-K^2 Sin^2θ)の角度微小角分割計算の精度を上げました。
2018/04/11
近似公式による計算に桁落ち対策を行い、精度の向上をしました。
離心率の値0.99999987程度(楕円比で１：０．０００５)迄、小数点以下13桁の精度で楕円積分が出来るようになりました。
2018/03/31
プログラムのランデン変換時の配列の大きさを最適化し、計算精度を上げました。
楕円の周長計算
x2/a2
+ y2/b2
= 1 の一般的な楕円の面積は、S = πab
で簡単に計算出来ますが、周長の計算は、単純には計算できません。
楕円周長の近似公式
周長 Lは無限級数で
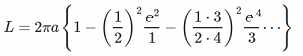
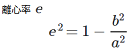
この近似計算の問題は、離心率が大きい(aとbの比が大きい)と計算時間が長くなります。
特に、離心率が1に近づくと、計算数が増えます。
離心率0.99999987で、約6000万回の繰り返しの計算が必要です。
弧長積分
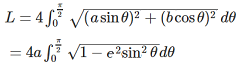sin2、cos2 でもπ/2迄の積分なので同じ結果になります。
このまゝでは、計算に不都合なので積分部分をランデン変換をします。
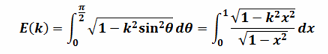
ランデン変換に関しては以前あったホームページ 楕円積分 数値計算ノート のEXCELのプログラムをDelphi用に変換して使用しています。
k は離心率です。
分割計算
１．角度を微小角度に分割 周上のx,y座標をから距離を計算加算して積分
Ｌ＝ の値を求めます。
２．0～a 又は 0～b
の間を分割して、xの値からyの値を求めて、微小角の距離を加算して周長を求めます。
精度よく計算する為には、100万分割程度必要で、計算に時間が掛かります。
楕円外周プラス１の計算
楕円の外周の鉛直方向に１プラスした線の周長計算。
楕円の周長に２π加算した値に成ることは分かっているのですが、一応プログラムを組んでみました。
角度の分割計算です。
プログラム
此処での計算はあくまでも楕円の周長の計算で、楕円弧の計算は、別途作成
青い線の楕円が基本の楕円で、外側の赤い線が、外側に1プラスした線で、基本的に楕円ではありません。
比率の変更により、外側へのプラス値は、自由に変更が出来ます。
一番精度の高いのは、完全楕円積分です。
不完全楕円積分に分割角度指定があるのは、分割角度により誤差が出るのと、楕円の半径bがゼロに近づくと、演算エラーが出るのを確認する為です。
基本的にランデン変換による不完全楕円積分は、K= 1 の時は、角度< 90°で K<1 の時は 角度<= 90°の範囲でないと正しい計算が出来ません。
90°以上でもKの値が小さい場合は、誤差は出ますが計算できる場合があります。
Kの値が小さいほど大きな角度まで計算が可能です。
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls;
type
TForm1 = class(TForm)
Image1: TImage;
arEdit: TLabeledEdit;
brEdit: TLabeledEdit;
Button1: TButton;
PlusdEdit: TLabeledEdit;
Image2: TImage;
Button2: TButton;
Button3: TButton;
Button4: TButton;
Button5: TButton;
Button6: TButton;
Button7: TButton;
CheckBox1: TCheckBox;
RadioButton1: TRadioButton;
RadioButton2: TRadioButton;
RadioButton3: TRadioButton;
procedure FormCreate(Sender: TObject);
procedure Button1Click(Sender: TObject);
procedure Button2Click(Sender: TObject);
procedure Button3Click(Sender: TObject);
procedure Button4Click(Sender: TObject);
procedure Button5Click(Sender: TObject);
procedure Button6Click(Sender: TObject);
procedure Button7Click(Sender: TObject);
private
{ Private 宣言 }
procedure imageClear(N: integer);
procedure Linedlaw(x1, y1, x2, y2: double; LF: boolean);
procedure draw_ellipse;
procedure ellipse_calc(ar, br, q: double; var x, y: double);
procedure ellipsePlus(ar, br, q: double; var x, y: double; RF: boolean);
function EllipseInput(var ar, br: double): boolean;
function Second_Perfect_elliptic_integral(K: double): double;
function second_imperfect_elliptic_integral(K, Q: double): double;
procedure spotimageClear(Top: integer);
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses Math;
var
Xsift, Ysift : integer;
magnification : double;
const
draw_margin = 30;
//-----------------------------
// 表示画像消去
//-----------------------------
procedure TForm1.imageClear(N: integer);
begin
if N and 1 = 1 then begin
image1.Canvas.Brush.Style := bsSolid;
image1.Canvas.Brush.Color := clWhite;
image1.Canvas.FillRect(Rect(0, 0, image1.Width, image1.Height));
end;
if N and 2 = 2 then begin
image2.Canvas.Brush.Style := bsSolid;
image2.Canvas.Brush.Color := clWhite;
image2.Canvas.FillRect(Rect(0, 0, image1.Width, image1.Height));
end;
end;
procedure TForm1.spotimageClear(Top: integer);
begin
image2.Canvas.Brush.Style := bsSolid;
image2.Canvas.Brush.Color := clWhite;
image2.Canvas.FillRect(Rect(0, Top, image1.Width, Top + 20));
end;
//--------------------------
// ２点間線引き
//--------------------------
procedure TForm1.Linedlaw(x1, y1, x2, y2: double; LF: boolean);
var
xp1, yp1, xp2, yp2: integer;
begin
if LF then begin
xp1 := round(x1) + Xsift;
yp1 := image2.Height - round(y1) - Ysift;
image2.Canvas.MoveTo(xp1, yp1);
end;
xp2 := round(x2) + Xsift;
yp2 := image2.Height - round(y2) - Ysift;
image2.Canvas.LineTo(xp2, yp2);
end;
//---------------------------------
// 楕円計算 q 角度
// ar , br 半径
//---------------------------------
procedure TForm1.ellipse_calc(ar, br, q: double; var x, y: double);
begin
x := ar * cos(q) * magnification;
y := br * sin(q) * magnification;
end;
//------------------------------------------------------
// 外周加算値計算
// 加算値は１として一定
// 半径の方を相対的に計算 別途スケール設定を必要とします
// magnificationは作図ための倍率
//------------------------------------------------------
procedure TForm1.ellipsePlus(ar, br, q: double; var x, y: double; RF: boolean);
var
x0, y0 : double;
Rtsxsy : double;
begin
x0 := ar * cos(q);
y0 := br * sin(q);
Rtsxsy := ar * ar * sin(q) * sin(q) + br * br * cos(q) * cos(q);
Rtsxsy := sqrt(Rtsxsy);
x := x0 + br * cos(q) / Rtsxsy;
y := y0 + ar * sin(q) / Rtsxsy;
if not RF then begin
x := x * magnification;
y := y * magnification;
end;
end;
//--------------------
// 楕円の値入力処理
//--------------------
function TForm1.EllipseInput(var ar, br: double): boolean;
var
ch : integer;
begin
result := false;
val(arEdit.Text, ar, ch);
if ch <> 0 then begin
application.MessageBox('半径aは数値ではありません。', '半径a', 0);
exit;
end;
if ar <= 0 then begin
application.MessageBox('半径aがゼロ 又はゼロ以下です。', '半径a', 0);
exit;
end;
val(brEdit.Text, br, ch);
if ch <> 0 then begin
application.MessageBox('半径bは数値ではありません。', '半径b', 0);
exit;
end;
if br <= 0 then begin
application.MessageBox('半径bがゼロ 又はゼロ以下です。', '半径b', 0);
exit;
end;
result := true;
end;
//---------------------------------------------------
// 楕円と楕円の外側の垂直方向に１加算した位置に線引き
// 加算値が１でない場合は楕円側の大きさを１との比率で
// 変更し計算します。
// 加算作図した図形は楕円ではありません。
//---------------------------------------------------
procedure TForm1.draw_ellipse;
const
divideN = 2000; // 作図用分割数
divideM = 12; // 値表示用分割数
Tpich = 15; // 値表示ピッチ
var
ch : integer;
ar, br : double;
maxr : double;
I, J, K : integer;
dq : double;
x1, y1 : double;
x2, y2 : double;
plusd : double;
scale : double;
Ind, L : integer;
XYLL : array[0..divideM - 1] of array[0..2] of string;
NoS : string;
begin
if not EllipseInput(ar, br) then exit;
val(plusdEdit.Text, plusd, ch);
if ch <> 0 then begin
application.MessageBox('外周加算値は数値ではありません。', '外周加算値', 0);
exit;
end;
if plusd <= 0 then begin
application.MessageBox('外周加算値がゼロ 未満です。', '外周加算値', 0);
exit;
end;
// 作図計算ピッチ計算
dq := 2 * pi / divideN;
// 半径と外周加算値のスケール設定
scale := 1 / plusd;
ar := ar * scale;
br := br * scale;
// 大きい方の半径選択
maxr := ar;
if br > ar then maxr := br;
// 作図倍率設定
magnification := (Xsift - draw_margin) / (maxr + 1);
// 楕円作図
image2.Canvas.Pen.Style := psSolid;
image2.Canvas.Pen.Color := clBlue;
ellipse_calc(ar, br, -dq, x1, y1);
for I := 0 to divideN do begin
ellipse_calc(ar, br, dq * I, x2, y2);
if I = 0 then Linedlaw(x1, y1, x2, y2, True)
else Linedlaw(x1, y1, x2, y2, False);
x1 := x2;
y1 := y2;
end;
// 外周加算値作図
image2.Canvas.Pen.Color := clRed;
ellipsePlus(ar, br, -dq, x1, y1, False);
for I := 0 to divideN do begin
ellipsePlus(ar, br, dq * I, x2, y2, False);
if I = 0 then Linedlaw(x1, y1, x2, y2, True)
else Linedlaw(x1, y1, x2, y2, False);
x1 := x2;
y1 := y2;
end;
// 中心線作図
image2.Canvas.Pen.Style := psDashDot;
image2.Canvas.Pen.Color := clGreen;
Linedlaw(-50, 0, 50, 0, True);
Linedlaw( 0, -50, 0, 50, True);
// 外周値表示
// 表示ビッチ角度設定
dq := 2 * pi / divideM;
// 外周値テキスト変換
for I := 0 to divideM - 1 do begin
ellipsePlus(ar, br, dq * I, x1, y1, True);
x1 := x1 / scale;
y1 := y1 / scale;
XYLL[I, 0] := floatTostrF(x1, ffFixed, 10,6);
XYLL[I, 1] := floatTostrF(y1, ffFixed, 10,6);
XYLL[I, 2] := floatTostrF(dq * I / pi * 180, ffFixed, 10,3);
end;
// 小数点の位置の最大値検索
ind := 0;
for I := 0 to divideM - 1 do
for J := 0 to 2 do begin
if pos('.',XYLL[I, J]) > ind then ind := pos('.', XYLL[I, J]);
end;
// 小数点の位置に応じて先頭にスペース追加
for I := 0 to divideM - 1 do
for J := 0 to 2 do begin
K := ind - pos('.',XYLL[I, J]);
for L := 0 to K do begin
XYLL[I, J] := ' ' + XYLL[I, J];
end;
end;
// 値表示
for I := 0 to divideM - 1 do begin
NoS := inttostr(I + 1) + '=';
if I < 9 then NoS := ' ' + NoS;
image1.Canvas.TextOut( 10, Tpich * I + 5, 'X' + NoS + XYLL[I, 0]);
image1.Canvas.TextOut(160, Tpich * I + 5, 'Y' + NoS + XYLL[I, 1]);
image1.Canvas.TextOut(310, Tpich * I + 5, 'θ' + NoS + XYLL[I, 2] + '°');
end;
end;
//----------------------------------------------
// 楕円と外周加算ず作図
//----------------------------------------------
procedure TForm1.Button1Click(Sender: TObject);
begin
imageClear(3);
draw_ellipse;
end;
//---------------------
// 楕円の外周長計算1
// 楕円級数使用
// Kの値 0.999999 迄
//---------------------
procedure TForm1.Button2Click(Sender: TObject);
const
pich = 15;
LoopD = 60000000;
var
I, J : integer;
ar, br : double;
a, b, eq, ek : double;
ak, bk, k : double;
s, bs : double;
s1, s2, s3, s4, s5: double;
ec, eka : double;
L : double;
NS : string;
outD : integer;
begin
if not EllipseInput(ar, br) then exit;
imageClear(1);
image1.Canvas.TextOut(10, 5, '近似級数使用');
if br > ar then begin
a := ar;
ar := br;
br := a;
end;
// e := sqrt(1 - br * br / ar / ar); // √e^2 離心率
// image1.Canvas.TextOut(10, 5, '級数使用');
eq := 1 - br * br / ar / ar; // e^2
k := sqrt(eq); // 離心率 e
image1.Canvas.TextOut(200, 5, 'K= ' + floatTostr(K));
s1 := 0;
s2 := 0;
s3 := 0;
s4 := 0;
s5 := 0;
ek := eq;
a := 1;
b := 2;
ak := 1;
s := 1; // 離心率ゼロ 円の時の値をセットします。
bs := S5;
J := 0;
I := 1;
eka := 0;
outD := 1;
// 離心率eの値が0の場合は円なので計算しません。
if K <> 0 then begin
// LoopDで繰り返し計算上限設定
for I := 0 to LoopD do begin
bk := (a * a) / (b * b); // (1・3!!)^2 /(2・4!!) ^2
ak := ak * bk;
ec := ek / a; // (e^2・4!!) / (1・3!!)
eka := ak * ec;
// 値の大きさによって、桁落ちして加算されなくなるのを防止します。
if (1 > eka) and (eka >= 1E-4) then S1 := S1 + eka;
if (1E-4 > eka) and (eka >= 1E-7) then S2 := S2 + eka;
if (1E-7 > eka) and (eka >= 1E-10) then S3 := S3 + eka;
if (1E-10 > eka) and (eka >= 1E-13) then S4 := S4 + eka;
if 1E-13 > eka then S5 := S5 + eka;
s := 1 - s1 - s2 - s3 - s4 - s5;
// 1E-13より小さい値の部分が変化しなくなったら終了
// 加算の値ekaが1E-22～1E-25以下になると桁落ちし変化しなくなります。
if (S5 <> 0) and (S5 = bs) then break;
a := a + 2; // 1・3・5
b := b + 2; // 2・4・6
ek := ek * eq; // e^2・4!!
bs := S5;
if I mod outD = 0 then begin
inc(J);
NS := intTostr(J);
if length(NS) = 1 then NS := ' ' + NS;
L := 2 * pi * ar * s;
outD := outD * 2;
image1.Canvas.TextOut(10, J * pich + 25, 'No' + NS + ' ' + floattostr(L));
image1.Canvas.TextOut(180, J * pich + 25, 'eka= ' + floattostr(eka));
image1.Canvas.TextOut(370, J * pich + 25, 'Loop No ' + inttostr(I + 1));
end;
end;
end;
L := 2 * pi * ar * s; // 周長
inc(J);
NS := intTostr(J);
if length(NS) = 1 then NS := ' ' + NS;
image1.Canvas.TextOut(10, J * pich + 25, 'No' + NS + ' ' + floattostr(L));
image1.Canvas.TextOut(180, J * pich + 25, 'eka= ' + floattostr(eka));
image1.Canvas.TextOut(370, J * pich + 25, 'Loop No ' + inttostr(I - 1));
end;
//--------------------------------------------------
// 楕円の外周長計算２
// 角度等分割
// √(1-K^2 Sin^2θ) dθ は分割角度の中間の値(I+0.5)*dθ
// とする事により精度を上げます。
//--------------------------------------------------
procedure TForm1.Button3Click(Sender: TObject);
const
K = 1000000;
var
ar, br : double;
a, e2 : extended;
I : integer;
Q, dQ, S : extended;
X1, Y1, X2, Y2 : extended;
begin
if not EllipseInput(ar, br) then exit;
if br > ar then begin
a := ar;
ar := br;
br := a;
end;
S := 0;
Q := 0;
if Checkbox1.Checked then begin
dQ := pi / 2 / K;
e2 := 1 - br * br / ar / ar; // e^2
for I := 0 to K - 1 do begin
Q := (I + 0.5) * dQ; // (I + 0.5)中間の角度にして精度を上げます
S := S + sqrt(1 - e2 * sin(Q) * sin(Q)) * dQ;
end;
S := S * 4 * ar;
end
else begin
dQ := pi * 2 / K;
X1 := ar * cos(Q);
Y1 := br * sin(Q);
for I := 1 to K do begin
Q := I * dQ;
X2 := ar * cos(Q);
Y2 := br * sin(Q);
e2 := sqrt((X2 - X1) * (X2 - X1) + (Y2 - Y1) * (Y2 - Y1));
S := S + e2;
X1 := X2;
Y1 := Y2;
end;
end;
spotimageClear(20);
image2.Canvas.TextOut(10, 20,'角度等分割 ' + floattostr(S));
end;
//---------------------
// 楕円の外周長計算３
// 第２種完全楕円積分
// ランデン変換
//---------------------
function TForm1.Second_Perfect_elliptic_integral(K: double): double;
var
I, MI : integer;
kn : array of double; // kn
kdn : array of double; // k'n
kkn : array of double; // K(kn)
Ekn : array of double; // E(kn)
begin
MI := 0;
setlength(kn, MI + 1);
setlength(kdn, MI + 1);
// kn[0] := 0.9;
kn[0] := K;
kdn[0] := 0;
while Kn[MI] <> kdn[0] do begin
kdn[0] := kn[MI];
inc(MI);
setlength(kn, MI + 1);
Kn[MI] := (1 - sqrt(1 - kn[MI - 1] * kn[MI - 1]))/(1 + sqrt(1 - Kn[MI - 1] * Kn[MI - 1]));
end;
dec(MI);
setlength(kn, MI + 1); // kn
setlength(kdn, MI + 1); // k'n
setlength(kkn, MI + 1); // K(kn)
setlength(Ekn, MI + 1); // E(kn)
// for I := 1 to MI do Kn[I] := (1 - sqrt(1 - kn[I - 1] * kn[I - 1]))/(1 + sqrt(1 - Kn[I - 1] * Kn[I - 1]));
for I := 0 to MI do kdn[I] := sqrt(1 - kn[I] * kn[I]);
kkn[MI] := pi / 2;
for I := MI - 1 downto 0 do kkn[I] := (1 + Kn[I + 1]) * kkn[I + 1];
Ekn[MI] := pi / 2;
for I := MI - 1 downto 0 do Ekn[I] := (1 + kdn[I]) * Ekn[I + 1] - kdn[I] * kkn[I];
result := Ekn[0];
end;
//-------------------------
// 楕円の外周長計算３
//-------------------------
procedure TForm1.Button4Click(Sender: TObject);
var
ar, br, k, L :double;
begin
if not EllipseInput(ar, br) then exit;
if br > ar then begin
k := ar;
ar := br;
br := k;
end;
K := sqrt(1 - br * br / ar / ar); // k 離心率
// k := 0.9;
L := Second_Perfect_elliptic_integral(K); // 第２種完全楕円積分
spotimageClear(40);
image2.Canvas.TextOut(10, 40, '完全楕円積分 ' + floattostr(4 * ar * L));
end;
//---------------------
// 楕円の外周長計算４
// X方向等分割
//---------------------
procedure TForm1.Button5Click(Sender: TObject);
const
K = 1000000;
var
I : integer;
ar, br, a : double;
dx : double;
X1, Y1 : double;
x2, Y2 : double;
SL, L : double;
begin
if not EllipseInput(ar, br) then exit;
if br > ar then begin
a := ar;
ar := br;
br := a;
end;
dx := ar / K; // 距離の分割
X1 := ar;
Y1 := 0;
a := ar * ar;
L := 0;
for I := K - 1 downto 0 do begin // 90°分の距離計算
X2 := I * dx;
Y2 := sqrt((1 - X1 * X1 / a)) * br;
SL := sqrt((X2 - X1) * (X2 - X1) + (Y2 - Y1) * (Y2 - Y1));
L := L + SL;
X1 := X2;
Y1 := Y2;
end;
spotimageClear(60);
image2.Canvas.TextOut(10, 60, 'Ｘ方向等分 ' + floattostr(4 * L));
end;
//-------------------------------
// 第１種第２種不完全積分
// FBnKn[0] 第１種不完全積分解
// EBnKn[0] 第２種不完全積分解
// ランデン変換
// Q 角度 deg
// K 離心率
//-------------------------------
function TForm1.second_imperfect_elliptic_integral(K, Q: double): double;
var
I, MI : integer;
Kn : array of double; // Kn
knd : array of double; // k'n
N2SKn : array of double; // 2/(1+Kn)
T2SKnd : array of double; // П2/(1+Kn')
BRad : array of double; // β(rad)
SinBn : array of double; // sinβn
FBnKn : array of double; // F(βn,kn)
EBnKn : array of double; // E(βn,kn)
LnD : double;
begin
// K = 0 の時は円なのでpiの角度値をかえします。
if K = 0 then begin
result := pi * Q / 180;
exit;
end;
// 1 > K > 0 の時
MI := 0;
LND := 0;
setlength(kn, MI + 1); // kn
kn[0] := K;
while LND <> Kn[MI] do begin
LnD := Kn[MI];
inc(MI);
setlength(kn, MI + 1); // kn
kn[MI] := 2 * sqrt(Kn[MI - 1])/(1 + Kn[MI - 1]);
end;
Dec(MI);
setlength(kn, MI + 1); // kn
setlength(knd, MI + 1); // k'n
setlength(N2SKn, MI + 1); // 2/(1+Kn)
setlength(T2SKnd, MI + 1); // П2/(1+Kn')
setlength(BRad, MI + 1); // β(rad)
setlength(SinBn, MI + 1); // sinβn
setlength(FBnKn, MI + 1); // F(βn,kn)
setlength(EBnKn, MI + 1); // E(βn,kn)
knd[0] := 1;
for I := 1 to MI do
knd[I] := (1 - kn[I - 1]) / (1 + Kn[I - 1]);
for I := 0 to MI do
N2SKn[I] := 2 / (1 + kn[I]);
T2SKnd[MI] := N2SKn[MI];
for I := MI - 1 downto 0 do
T2SKnd[I] := T2SKnd[I + 1] * N2SKn[I];
BRad[0] := Q / 180 * pi;
for I := 1 to MI do
BRad[I] := (arcsin(kn[I - 1] * sin(Brad[I - 1])) + Brad[I - 1]) / 2;
for I := 0 to MI do
SinBn[I] := sin(Brad[I]);
LnD := LN((1 + sin(Brad[MI])) / cos(Brad[MI]));
for I := 0 to MI do
FBnKn[I] := T2SKnd[I] * LnD;
EBnKn[MI] := sin(Brad[MI]);
for I := MI - 1 downto 0 do
EBnKn[I] := (2 * EBnKn[I + 1] + 2 * knd[I + 1] * FBnKn[I + 1]) / (1 + knd[I + 1]) - kn[I] * SinBn[I];
result := EBnKn[0];
end;
//----------------------------------
// 第２種不完全積分による楕円周長
//----------------------------------
procedure TForm1.Button6Click(Sender: TObject);
var
ar, br, Q, K, L: double;
begin
Q := 0;
if Radiobutton1.Checked then Q := 90;
if Radiobutton2.Checked then Q := 180;
if Radiobutton3.Checked then Q := 360;
if not EllipseInput(ar, br) then exit;
if br > ar then begin
k := ar;
ar := br;
br := k;
end;
K := sqrt(1 - br * br / ar / ar); // k 離心率
L := second_imperfect_elliptic_integral(K, Q); // 第２種不完全積分
spotimageClear(80);
image2.Canvas.TextOut(10, 80, '不完全積分 ' + floattostr(ar * L));
if Q = 90 then
image2.Canvas.TextOut(250, 80, 'x4= ' + floattostr(ar * L * 4));
if Q = 180 then
image2.Canvas.TextOut(250, 80, 'x2= ' + floattostr(ar * L * 2));
if Q = 360 then
image2.Canvas.TextOut(250, 80, 'x1= ' + floattostr(ar * L));
end;
//-------------------------------------
// 外周１加算周長
//-------------------------------------
procedure TForm1.Button7Click(Sender: TObject);
const
divideN = 1000000;
var
ch, I : integer;
ar, br, plusd : double;
dQ, Q, scale : double;
X1, Y1 : double;
X2, Y2 : double;
L, Ls : double;
K, LB : double;
begin
if not EllipseInput(ar, br) then exit;
val(plusdEdit.Text, plusd, ch);
if ch <> 0 then begin
application.MessageBox('外周加算値は数値ではありません。', '外周加算値', 0);
exit;
end;
if plusd <= 0 then begin
application.MessageBox('外周加算値がゼロ 未満です。', '外周加算値', 0);
exit;
end;
if br > ar then begin
k := ar;
ar := br;
br := k;
end;
K := sqrt(1 - br * br / ar / ar); // k 離心率
LB := Second_Perfect_elliptic_integral(K); // 第２種完全楕円積分
LB := LB * 4 * ar; // 楕円周長
// 計算ピッチ計算
dQ := 2 * pi / divideN;
// 半径と外周加算値のスケール設定
scale := 1 / plusd;
ar := ar * scale;
br := br * scale;
Q := 0;
L := 0;
ellipsePlus(ar, br, Q, X1, Y1, True); // 楕円加算値上座標の計算
for I := 1 to divideN do begin
Q := I * dQ;
ellipsePlus(ar, br, Q, X2, Y2, True); // 楕円加算値上座標の計算
Ls := sqrt((X2 - X1) * (X2 - X1) + (Y2 - Y1) * (Y2 - Y1)); // 二点間距離
L := L + Ls; // 距離の合計
X1 := X2;
Y1 := Y2;
end;
L := L / scale;
spotimageClear(100);
spotimageClear(120);
image2.Canvas.TextOut(10, 100, '外周加算周長 ' + floattostr(L));
Ls := L - LB;
image2.Canvas.TextOut(250, 100, '周長差分 ' + floattostr(Ls));
image2.Canvas.TextOut(250, 120, '加算ｘ２π ' + floattostr(pi * 2 / scale));
end;
//-------------
// 初期設定
//-------------
procedure TForm1.FormCreate(Sender: TObject);
begin
Form1.Caption := 'EllipsePlusOne';
Width := 1110;
Height := 520;
image1.Top := 0;
image1.Left := 0;
image1.Height := ClientHeight;
image1.Width := ClientHeight;
image2.Top := 0;
image2.Left := image1.Width;
image2.Height := ClientHeight;
image2.Width := ClientHeight;
imageClear(3);
Xsift := image2.Width div 2;
Ysift := image2.Height div 2;
image1.Canvas.Font.Name := 'ＭＳ ゴシック';
image1.Canvas.Font.Height := 14;
image2.Canvas.Font.Name := 'ＭＳ ゴシック';
image2.Canvas.Font.Height := 14;
end;
end.
EllipsePlusOne.zip