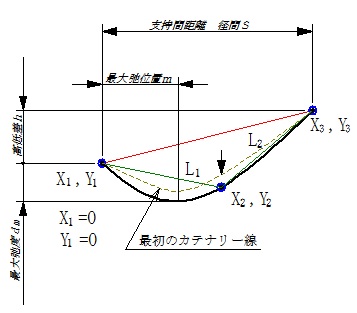
左図X2,Y2が通過を指定した位置です。最初に、三点を結ぶ放物線距離をけいさんします。
これを、最初の懸垂線の長さとします。
三点を通る懸垂線は、必ず放物線で結んだ長さより長くなるので、少しずつ長くして、指定点を通るようにします。
円であれば、連立方程式を解けば良いのですが、能力不足で、解けそうにないので、ＰＣの計算速度に頼ることにしました。
通過点指定の懸垂線
懸垂線の両端の位置だけでなく、通過点を指定した場合の懸垂線の長さ、カテナリー数を計算します。
左図X2,Y2が通過を指定した位置です。
最初に、三点を結ぶ放物線距離をけいさんします。
これを、最初の懸垂線の長さとします。
三点を通る懸垂線は、必ず放物線で結んだ長さより長くなるので、少しずつ長くして、指定点を通るようにします。
円であれば、連立方程式を解けば良いのですが、能力不足で、解けそうにないので、ＰＣの計算速度に頼ることにしました。
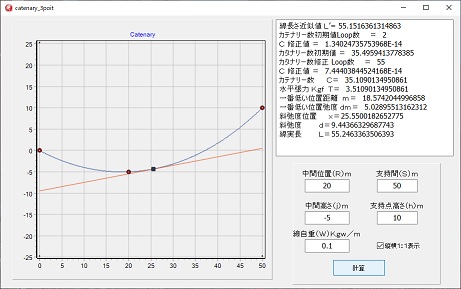左図がプログラムの実行画面です。
通常の懸垂線プログラムに、途中の通過点を指定する入力項目を追加してあります。
まず、最初に直線で結んだ距離を計算し、両端の直線距離と等しくないか確認します。
長ければ、最初に、近似値として放物線で結んだ長さを計算し、仮の長さとして、カテナリー数を計算します。
次に、カテナリー数を微調整して、懸垂線として、指定点を通るカテナリー数を求めます。
プログラム
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls,
VclTee.TeeGDIPlus, VCLTee.TeEngine, VCLTee.Series, VCLTee.TeeProcs,
VCLTee.Chart;
type
TForm1 = class(TForm)
Memo1: TMemo;
Panel1: TPanel;
W_Edit: TLabeledEdit;
h_Edit: TLabeledEdit;
S_Edit: TLabeledEdit;
Chart1: TChart;
Series1: TLineSeries;
Series2: TPointSeries;
Button1: TButton;
CheckBox1: TCheckBox;
Series3: TLineSeries;
Series4: TPointSeries;
R_Edit: TLabeledEdit;
J_Edit: TLabeledEdit;
Series5: TPointSeries;
procedure Button1Click(Sender: TObject);
private
{ Private 宣言 }
function datainput: boolean;
procedure Drawing;
function f(Ct, S, sL2mh2: double): double;
function dfdc(Ct, S: double): double;
function inversed(S, sL2mh2: double): double;
function inverse_newton(S, sL2mh2: double): double;
function solve_a(S, h, L: double): double;
function calc_C: double;
function calc_C_Def(Cs: double): double;
function cubic_equation_length: double;
function calc_arc(a1, b1, c1: double): double;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses
system.Math;
var
S : double; // 支持間 m
R : double; // 中間点
h : double; // 高低差 m
j : double; // 中間点高さ
W : double; // 線自重 kgw/m
T : double; // 線張力 kgf
C : double; // カテナリー数
d : double; // 弛度 m
m : double; // 最大たるみ位置 m
dm :double; // 最大たるみ位置 弛度 m
x : double; // 斜弛度地点までの距離 m
L : double; // 線実長
// 入力処理
function TForm1.datainput: boolean;
var
ch: integer;
begin
result := false;
val(R_edit.Text, R, ch);
if (ch <> 0) or (R <= 0) then begin
application.MessageBox('中間点に間違いがあります。','注意',0);
exit;
end;
val(j_edit.Text, j, ch);
if (ch <> 0) then begin
application.MessageBox('中間点高さに間違いがあります。','注意',0);
exit;
end;
val(S_edit.Text, S, ch);
if (ch <> 0) or (S <= 0) then begin
application.MessageBox('支持間に間違いがあります。','注意',0);
exit;
end;
val(h_edit.Text, h, ch);
if ch <> 0 then begin
application.MessageBox('支持点高さに間違いがあります。','注意',0);
exit;
end;
if h / S * R <= j then begin
application.MessageBox('中間点の高さが高すぎます。','注意',0);
exit;
end;
if (R >= S) or (R <= 0) then begin
application.MessageBox('中間点の位置が支持間の外側です。','注意',0);
exit;
end;
val(W_edit.Text, W, ch);
if (ch <> 0) or (W <= 0) then begin
application.MessageBox('線自重に間違いがあります。','注意',0);
exit;
end;
result := true;
end;
// 懸垂線作図
// 低い方の支持位置基準
procedure TForm1.Drawing;
const
K = 500;
var
xn : double;
x, dx : double;
y : double;
i : integer;
begin
dx := S / K;
// 懸垂線作図
for i := 0 to K do begin
xn := i * dx; // 計算位置
x := abs(xn - m); // 最大弛み位置からの距離
y := C * (cosh(x / C) - 1) - dm; // 高さ 低い方の支持位置を基準として計算
Series1.AddXY(xn, y);
end;
// 斜弛み位置通過接線
Series3.AddXY(0, 0 - d); // 斜弛み位置通過傾斜線 低い方
Series3.AddXY(S, h - d); // 斜弛み位置通過傾斜線 高い方
// 支持位置 斜弛度地点 丸表示
Series4.AddXY(0, 0); // 低い方の支持位置
Series4.AddXY(R, j);
Series4.AddXY(S, h); // 高い方の支持位置
x := m + C * arcsinh(h / S); // 斜弛度地点距離 x
y := h / S * x - d; // 斜弛度y座標
Series5.AddXY(x, y); // 斜弛度xy
end;
// --------- カテナリー数計算 ニュートン法 -----------------------
// 誤差計算 2.0 * Ct * sinh(S / (Ct * 2.0)) = sqrt(L^2-h^2)
function TForm1.f(Ct, S, sL2mh2: double): double;
begin
result := 2.0 * Ct * sinh(S / (2.0 * Ct)) + sL2mh2;
end;
// 微分計算 ∂/∂Ct
function TForm1.dfdc(Ct, S: double): double;
begin
result := 2.0 * sinh(S / (2.0 * Ct)) - S * cosh(S / (2.0 * Ct)) / Ct;
end;
// カテナりー数近似値計算
function TForm1.inversed(S, sL2mh2: double): double;
var
a0, b0, c0: double;
begin
a0 := sL2mh2 + S;
b0 := power(S, 3) / 24;
c0 := power(S, 5) / 1920;
result := sqrt((-b0 - sqrt(b0 * b0 - 4 * a0 * c0)) / 2 / a0);
end;
// カテナりー数計算
function TForm1.inverse_newton(S, sL2mh2: double): double;
const
Kp = 1000;
var
Ct : double;
fvalue : double;
eps : double;
i, n : integer;
begin
eps := 1.0E-15 * L; // 判定値
Ct := inversed(S, sL2mh2); // カテナりー数近似値計算
fvalue := f(Ct, S, sL2mh2); // 誤差計算
n := 0;
for i := 0 to Kp do begin
Ct := Ct - fvalue / dfdc(Ct, S); // ニュートン法漸化計算
fvalue := f(Ct, S, sL2mh2); // 誤差計算
inc(n); // カウンターインクリメント
if abs(fvalue) < eps then break; // 収束判定
end;
memo1.Lines.Add('カテナリー数初期値Loop数 ＝ ' + intTostr(n));
memo1.Lines.Add('Ｃ 修正値 ＝ ' + floatTostr(abs(fvalue)));
if n > kp then begin
memo1.Lines.Add('カテナリー数収束せずループ数超えました。');
memo1.Lines.Add('線の長さが直線距離に近すぎるか長すぎます。');
Ct := 0;
end;
if Ct < 0 then begin
memo1.Lines.Add('線の長さが直線距離に近すぎます。');
end;
result := Ct;
end;
// ニュートン法計算スタート
function TForm1.solve_a(S, h, L: double): double;
begin
result := inverse_newton(S, -sqrt(L * L - h * h));
end;
//--------------------------------------------------------------
// 弓形部長さ計算
// 右と左に分けて計算
function TForm1.calc_arc(a1, b1, c1: double): double;
var
L0, L1, L2 : double;
s1, s2 : double;
a3, b3 : double;
a4, b4 : double;
xc0, yc0 : double;
begin
xc0 := -b1 / a1 / 2; // 放物線 変曲点X 中心位置
yc0 := xc0 * xc0 * a1 + xc0 * b1 + c1; // 変曲点y 中心位置
b3 := abs(0 - xc0) * 2;
a3 := abs(0 - yc0); // 放物線のx1の高さ
if a3 <> 0 then begin
s1 := sqrt(b3 * b3 + 16 * a3 * a3);
L1 := s1 / 2 + b3 * b3 / 8 / a3 * ln((4 * a3 + s1) / b3);
end
else L1 := 0;
b4 := abs(S - xc0) * 2;
a4 := abs(h - yc0); // 放物線のx2の高さ
if a4 <> 0 then begin
s2 := sqrt(b4 * b4 + 16 * a4 * a4);
L2 := s2 / 2 + b4 * b4 / 8 / a4 * ln((4 * a4 + s2) / b4);
end
else L2 := 0;
if (0 - xc0) * (S - xc0) > 0 then L0 := abs(L2 - L1) / 2
else L0 := (L1 + L2) / 2;
memo1.Lines.Add('線長さ近似値 Ｌ’= ' + floatTostr(L0));
result := L0;
end;
// 三点から二次関数変換と長さ計算
// ax^2 + bx + c = 0
function TForm1.cubic_equation_length: double;
var
x1, y1 : double;
x2, y2 : double;
x3, y3 : double;
a, b, c : double;
begin
x1 := 0;
y1 := 0;
x2 := R;
y2 := j;
x3 := S;
y3 := h;
a := ((y1-y2)*(x1-x3)-(y1-y3)*(x1-x2))/((x1-x2)*(x1-x3)*(x2-x3)); // ax^2
b := (y1-y2)/(x1-x2)-a*(x1+x2); // bx
c := y1-a*x1*x1-b*x1; // c
result := calc_arc(a, b, c); // 三点を結ぶ長さ計算
end;
// カテナりー数計算
function TForm1.calc_C: double;
var
Lc : double;
L0, L1: double;
begin
L0 := sqrt(R * R + j * j); // 中間位置直線距離
L1 := sqrt((S - R) * (S - R) + (h - j) * (h - j)); // 中間位置と支持位置直線距離
Lc := sqrt(S * S + h * h); // 支持間距離直線距離
L := L0 + L1; // 直線で結んだ場合の距離
if (L - Lc) < 1.0E-8 * L then begin
result := 0; // 距離の差が小さかったら0
memo1.Lines.Add('線の長さが直線距離に近すぎます。');
end
else begin
L := cubic_equation_length; // 二次曲線による近似長さ計算
result := solve_a(S, h, L); // カテナリー数初期値
end;
end;
// 中間指定位置へのカテナリー数収束計算
function TForm1.calc_C_Def(Cs: double): double;
var
df, dc: double;
dh : double;
Rh : double;
Rm : double;
Rx : double;
Sm, S2: Double;
CsB : Double;
DCF : boolean;
n : integer;
begin
memo1.Lines.Add('カタナリー数初期値 ＝ ' + floatTostr(Cs));
application.ProcessMessages;
df := 1.0E-15 * L; // 収束判定値
S2 := S / 2;
m := S2 - Cs * arcsinh(h / (2 * Cs * sinh(S2 / Cs))); // 一番低い位置
Sm := abs(m);
Rm := Cs * cosh(Sm / Cs); // 一番低い位置の高さ計算
Rx := abs(R - m); // 一番低い位置からの距離
Rh := Cs * cosh(Rx / Cs) - Rm; // 高さ 低い方の支持位置を基準として計算
dc := Cs / 125; // カテナリー数補正値初期値
DCF := True;
if j > Rh then DCF := False; // 中間点指定高さより低かったらFalse
n := 0; // カウンタークリア
repeat
CsB := Cs; // カテナリー数バックアップ
m := S2 - Cs * arcsinh(h / (2 * Cs * sinh(S2 / Cs))); // 一番低い位置
Sm := abs(m);
Rm := Cs * cosh(Sm / Cs); // 一番低い位置の高さ計算
Rx := abs(R - m); // 一番低い位置からの距離
Rh := Cs * cosh(Rx / Cs) - Rm; // 高さ 低い方の支持位置を基準として計算
dh := Rh - j; // 指定位置の高さの差
if DCF then begin
if dh > 0 then Cs := Cs - dc; // 線の位置が高かったらカテナリー数減算
if dh < 0 then begin // 線の位置が低くなったら
Cs := Cs + dc; // カテナリー数戻し
dc := dc * 0.2; // 補正値5分の1
Cs := Cs - dc; // カテナリー数新しい補正値で減算
end;
end
else
begin
if dh < 0 then Cs := Cs + dc; // 線の位置が低かったらカテナリー数加算
if dh > 0 then begin // 線の位置が高くなったら
Cs := Cs - dc; // カテナリー数戻し
dc := dc * 0.2; // 補正値5分の1
Cs := Cs + dc; // カテナリー数新しい補正値で加算
end;
end;
inc(n); // ループカウントインクリメント
// 収束判定値 ループ回数上限 カテナリー数変化なしで 収束判定
until (abs(dh) < df) or (n > 1000) or (Csb = Cs);
memo1.Lines.Add('カタナリー数修正 Loop数 ＝ ' + intTostr(n));
memo1.Lines.Add('Ｃ 修正値 ＝ ' + floatTostr(abs(dc)));
result := Cs;
end;
// 懸垂線計算の実行
procedure TForm1.Button1Click(Sender: TObject);
var
s1,Cs : double;
lmin, lmax : double;
bmin, bmax : double;
mg : double;
begin
if not datainput then exit;
button1.Enabled := False;
application.ProcessMessages;
memo1.Clear;
Cs := calc_C; // 仮のカテナリー数計算
if Cs <= 0 then begin
button1.Enabled := True;
exit;
end;
C := calc_C_Def(Cs); // 中間指定高さのカテナリー数計算
memo1.Lines.Add('カテナリー数 Ｃ＝ ' + floatTostr(C));
T := C * W;
memo1.Lines.Add('水平張力 Ｋｇｆ Ｔ＝ ' + floatTostr(T));
m := S / 2 - C * arcsinh(h / (2 * C * sinh(S / 2 / C)));
memo1.Lines.Add('一番低い位置距離 ｍ＝ ' + floatTostr(m));
s1 := abs(m * 2);
dm := C * (cosh(s1 / 2 / C) - 1);
memo1.Lines.Add('一番低い位置弛度 ｄｍ＝ ' + floatTostr(dm));
x := m + C * arcsinh(h / S);
memo1.Lines.Add('斜弛度位置 ｘ＝' + floatTostr(x));
d := x / S * h + C * (cosh(m / C) - cosh(arcsinh(h / S)));
memo1.Lines.Add('斜弛度 ｄ＝' + floatTostr(d));
L := C * (sinh(m / C) + sinh((S - m) / C));
memo1.Lines.Add('線実長 Ｌ＝' + floatTostr(L));
// グラフスケール計算
if h < 0 then begin
lmin := h - d;
lmax := 0;
end
else begin
lmin := -d;
lmax := h;
end;
bmin := 0;
bmax := S;
// グラフ縦横スケール設定
if bmax > lmax - lmin then begin
mg := (bmax - (lmax - lmin)) / 2;
lmax := lmax + mg;
lmin := lmin - mg;
end
else begin
mg := ((lmax - lmin) - bmax) / 2;
bmin := bmin - mg;
bmax := bmax + mg;
end;
Series1.Clear;
Series2.Clear;
Series3.Clear;
Series4.Clear;
Series5.Clear;
application.ProcessMessages;
if checkbox1.Checked then begin
Series2.AddXY(bmin, lmax);
Series2.AddXY(bmin, lmin);
Series2.AddXY(bmax, lmin);
end;
application.ProcessMessages;
Drawing;
button1.Enabled := True;
end;
end.
catenary_3point.zip