カテナリー曲線と指定点を通る直線の接線
指定点X座標=d、Ｙ座標=bを通る直線と、カテナリー曲線の接線を求める計算です。
直線と、カテナリー曲線の連立方程式をたて、べき級数展開式にして、ＤＫＡ法で、交点のX座標を求めます。
複素数の値がゼロに近いものが答えとなります。
冪級数展開は、答えが二つなので、偶数次数とします、奇数次数にすると、不要な答えが一つ増えてしまいます。
奇数次数項と、偶数次数項では、計算が違うので注意が必要です。
傾きが指定された直線の場合は、簡単に計算が出来ましたが、通過点を指定された直線の場合は、簡単に求める事出来そうにありません。
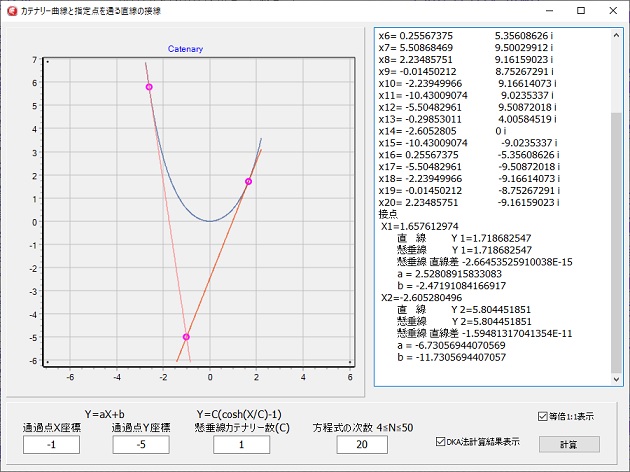ＤＫＡ法での計算結果は、Ｘ座標なので、そのＸの値から、カテナリー曲線のＹの値と、直線のYの値を求めて、Yの差分を誤差としています。
次数を大きくした方が精度は上がりますが、大きくしすぎるとオーバーフローが発生します。
プログラム
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls,
VclTee.TeeGDIPlus, VCLTee.TeEngine, VCLTee.Series, VCLTee.TeeProcs,
VCLTee.Chart;
type
TForm1 = class(TForm)
Memo1: TMemo;
Panel1: TPanel;
d_Edit: TLabeledEdit;
b_Edit: TLabeledEdit;
C_Edit: TLabeledEdit;
Chart1: TChart;
Series1: TLineSeries;
Series2: TPointSeries;
Button1: TButton;
Series3: TLineSeries;
Label1: TLabel;
Label2: TLabel;
CheckBox1: TCheckBox;
Series4: TPointSeries;
degreeEdit: TLabeledEdit;
CheckBox2: TCheckBox;
Series5: TLineSeries;
procedure Button1Click(Sender: TObject);
private
{ Private 宣言 }
function datainput: boolean;
procedure Drawing(yyt, yyb: double; j: integer);
procedure dataset(n: integer;var ab: array of double);
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses
system.Math;
var
C : double; // カテナリー数
d : double; // X座標
b : double; // Y座標
deg : integer; // 方程式の次数
xs, xe: double; // X軸の範囲
yt: double; // y軸の範囲
a1, a2 : double; // 直線の傾き
// Durand Kerner Aberth algorithm
function dka(a : array of double; var cr, ci: array of double; n: integer): boolean;
var
r, r0, t : double;
e, f1, f2, w1, w2 : double;
p1, p2, a1, a2, norm: double;
i, j, L: integer;
ca : array of double;
zc : double;
StrText : string;
eps : double;
begin
result := true;
setlength(ca, n + 1);
for i := 0 to n do ca[i] := a[i];
zc := - ca[n-1] / n;
for i := 1 to n do
for j := n downto i do
ca[j-1] := ca[j-1] + ca[j] * zc;
r := 0;
for i := 0 to n - 1 do begin
r0 := power(n * abs(ca[i]), 1/(n-i));
if r < r0 then r := r0;
end;
Form1.Memo1.Lines.Add('R = ' + floatTostr(r));
eps := 1E-15 * r; // 収束判定値半径で調整
for i := 1 to n do begin // 半径rの円に等間隔に配置する
t := 2 * PI / n * (i - 3.0 / 4.0);
cr[i-1] := -a[n-1] / n + r * cos(t); // アーバスの初期値
ci[i-1] := r * sin(t);
end;
L := 0;
try
repeat
e := 0;
for i := 0 to n -1 do begin
f1 := 1; // 分子 f(zi)、実部=f1,虚部=f2
f2 := 0; // ※a[n]=1
for j := n-1 downto 0 do begin // ホーナー法 f(z)=( … ((z+a[n-1])*z+a[n-2])*z+a[n-3])* … +a[1])*z+a[0]
w1 := f1 * cr[i] - f2 * ci[i]; // f*z=(f1+i*f2)*(x1+i*x2)=(f1*x1-f2*x2)+i*(f1*x2+f2*x1)
w2 := f2 * cr[i] + f1 * ci[i];
f1 := w1 + a[j]; // f=z+a[j]
f2 := w2;
end;
p1 := 1; // 分母 Π[j=1,N,i≠j](zi-zj)、実部=p1,虚部=p2
p2 := 0;
for j := 0 to n - 1 do begin
if j <> i then begin
w1 := p1 * (cr[i] - cr[j]) - p2 * (ci[i] - ci[j]); // p*(zi-zj)
w2 := p1 * (ci[i] - ci[j]) + p2 * (cr[i] - cr[j]);
p1 := w1; // p=(zi-zj)
p2 := w2;
end;
end;
t := p1 * p1 + p2 * p2; // 分子÷分母 (f1+i*f2)/(p1+i*p2)=(f1+i*f2)(p1-i*p2)/(p1*p1+p2*p2)
if t = 0 then begin
application.MessageBox('０では割れません。(DKAルーチン)', '注意', 0);
result := false;
exit;
end;
a1 := (f1 * p1 + f2 * p2) / t;
a2 := (f2 * p1 - f1 * p2) / t;
norm :=sqrt(a1 * a1 + a2 * a2);
if e < norm then e := norm; // 最大値
cr[i] := cr[i] - a1; // k回目の近似根 zi[k+1]=zi[k]-f(zi[k])/Π[j=1,N,i≠j](zi[k]-zj[k])
ci[i] := ci[i] - a2;
end;
inc(L);
until (e < eps) or (L > 400);
except
on E: Exception do begin
StrText := E.ClassName + sLineBreak + E.Message;
StrText := StrText + #13#10 + 'DKA法計算ルーチン';
StrText := StrText + sLineBreak + 'オーバーフローだったら次数を下げて計算してみてください。';
Application.MessageBox(PChar(StrText), '情報', MB_ICONINFORMATION);
result := False;
end;
end;
Form1.Memo1.Lines.Add('DKA法 Loop = ' + intTostr(L))
end;
// 入力処理
function TForm1.datainput: boolean;
var
ch: integer;
begin
result := false;
val(C_edit.Text, C, ch);
if (ch <> 0) or (C <= 0) then begin
application.MessageBox('カテナリー数に間違いがあります。','注意',0);
exit;
end;
val(d_edit.Text, d, ch);
if ch <> 0 then begin
application.MessageBox('通過点Ｘ座標に間違いがあります。','注意',0);
exit;
end;
val(b_edit.Text, b, ch);
if (ch <> 0) then begin
application.MessageBox('通過点Ｙ座標に間違いがあります。','注意',0);
exit;
end;
val(degreeedit.Text, deg, ch);
if (ch <> 0) then begin
application.MessageBox('方程式の次数に間違いがあります。','注意',0);
exit;
end;
if deg > 50 then begin
application.MessageBox('方程式の次数の値が大きすぎます（５０迄）。','注意',0);
exit;
end;
if deg < 4 then begin
application.MessageBox('方程式の次数の値が小さすぎます（４以上）。','注意',0);
exit;
end;
result := true;
end;
// 懸垂線 接線作図
// yyt グラフ上限 yyb グラフ下限
// J = 2 接線作図 J <> 2 接線無し
procedure TForm1.Drawing(yyt, yyb: double; j: integer);
const
K = 500;
var
xn : double;
x, dx : double;
y : double;
i : integer;
begin
dx := (xe - xs) / K;
// 懸垂線 接線作図
for i := -50 to K + 50 do begin
xn := i * dx + xs; // 計算位置
x := abs(xn);
y := C * (cosh(x / C) - 1); // カテナリー曲線
if (y < yyt) and (y >= yyb) then Series1.AddXY(xn, y);
if j = 2 then begin
y := a1 * (xn - d) + b; // 直線
if (y < yyt) and (y >= yyb) then Series3.AddXY(xn, y);
y := a2 * (xn - d) + b; // 直線
if (y < yyt) and (y >= yyb) then Series5.AddXY(xn, y);
end;
end;
end;
// cosh sinh値用N次元データー作成
procedure TForm1.dataset(n: integer; var ab: array of double);
var
i : integer;
function factorial(n: integer): double; // n!
var
j : integer;
begin
result := 1;
for j := 2 to n do result := result * j;
end;
begin
ab[0] := -b; // 定数項
for i := 1 to n do begin
if i mod 2 = 0 then ab[i] := (1 / factorial(i) - 1 / factorial(i - 1)) / power(C, i - 1) // 偶数次数項
else ab[i] := d / factorial(i) / power(C, i); // 奇数次数項
end;
end;
// カテナリー線と直線の交点計算の実行
procedure TForm1.Button1Click(Sender: TObject);
var
ab : array of double; // 次数データー
cr : array of double; // 実数部
ci : array of double; // 虚数部
i, n, j, ch: integer;
fd : double;
li : int64;
scou : string;
x : array of double; // 解法結果X値
ys : array of double; // 直線y値
yc : array of double; // カテナリー線Y値
xxs, xxe : double; // グラフx範囲
yyb, yyt : double; // グラフy範囲
StrText : string;
// 丸め
procedure roundfd(var d: double);
begin
if abs(d) < 1E5 then begin
li := round(d * 1E8); // 小数点8桁以下丸め
d := li / 1E8;
end;
end;
begin
Button1.Enabled := False;
xs := -1;
xe := 1;
// データー入力処理
if not datainput then begin
Button1.Enabled := true;
exit;
end;
n := deg;
// 次数で配列の確保
setlength(ab, n + 1);
setlength(cr, n);
setlength(ci, n);
setlength(x, 3);
setlength(ys, 2);
setlength(yc, 2);
// 配列にデーターセット sinh cosh
dataset(n, ab);
j := 0;
// 配列先頭の値を１に設定
if ab[n] = 0 then begin
memo1.Clear;
memo1.Lines.Add('DKA法');
memo1.Lines.Add(' データー配列の先頭の値が０（ゼロ）です。');
memo1.Lines.Add(' 次数を偶数にして下さい。');
Button1.Enabled := True;
exit;
end;
try
for i := n - 1 downto 0 do begin
ab[i] := ab[i] / ab[n];
end;
except
on E: Exception do begin // オーバーフロー処理
StrText := E.ClassName + sLineBreak + E.Message;
StrText := StrText + #13#10 + '配列の先頭を１にする処理';
Application.MessageBox(PChar(StrText), '情報', MB_ICONINFORMATION);
j := 1;
end;
end;
if j = 1 then begin // オーバーフローが有ったら此処迄
Button1.Enabled := True;
exit;
end;
ab[n] := 1;
memo1.Clear;
Series1.Clear;
Series2.Clear;
Series3.Clear;
Series4.Clear;
Series5.Clear;
application.ProcessMessages; // Clear待ち
memo1.Lines.Add('DKA法 次数 = ' + intTostr(n));
// dka法 計算
if not dka(ab, cr, ci, n) then begin // エラーが有ったら此処迄
Button1.Enabled := true;
exit;
end;
// dka法 答え表示
if checkbox2.Checked then
for i := 0 to n-1 do begin
fd := cr[i]; // 実数部
roundfd(fd); // 小数点8桁以下丸め
scou := 'x' + inttostr(i + 1) + '= ' + floatTostr(fd);
ch := length(scou);
ch := 28 - ch;
for j := 0 to ch do scou := scou + ' ';
fd := ci[i]; // 虚数部
roundfd(fd); // 小数点8桁以下丸め
memo1.Lines.Add(scou + floatTostr(fd) + ' i');
end;
// 接点の検出 虚数が小さい場所
ch := 0;
for i := 0 to n - 1 do begin
if abs(ci[i]) < 1E-8 then begin
fd := cr[i];
if ch <= 2 then begin
x[ch] := fd;
end;
inc(ch);
end;
end;
if ch = 0 then begin
memo1.Lines.Add('');
memo1.Lines.Add('接点を検出できませんでした。');
end;
if ch = 1 then begin
memo1.Lines.Add('');
memo1.Lines.Add('接点を分離できませんでした。');
memo1.Lines.Add('次数を偶数にして下さい。');
end;
if ch > 2 then begin
memo1.Lines.Add('');
memo1.Lines.Add('接点を正しく検出できませんでした。');
memo1.Lines.Add('次数を偶数にして下さい。');
memo1.Lines.Add('');
end;
// 次数が奇数の時は絶対値の一番大きい値をx[2]へ移動
if ch = 3 then begin
for n := 0 to 2 do
for i := 0 to 1 do begin
if abs(x[i]) > abs(x[i + 1]) then begin
fd := x[i];
x[i] := x[i + 1];
x[i + 1] := fd;
end;
end;
end;
if (ch = 2) or (ch = 3) then begin // 接線が有った場合の結果表示
memo1.Lines.Add('接点');
xs := x[0];
xe := x[1];
a1 := sinh(xs / C); // 直線1の傾斜
a2 := sinh(xe / C); // 直線2の傾斜
ys[0] := a1 * (xs - d) + b;
yc[0] := C * (cosh(xs / C) -1);
ys[1] := a2 * (xe - d) + b;
yc[1] := C * (cosh(xe / C) -1);
// 結果表示表示
for j := 0 to 1 do begin
memo1.Lines.Add(' X' + inttostr(j + 1) + '=' + floatTostrF(x[j],ffGeneral, 10, 8));
memo1.Lines.Add(' 直 線 Y ' + inttostr(j + 1) + '=' + floatTostrF(ys[j], ffGeneral, 10, 8));
memo1.Lines.Add(' 懸垂線 Y ' + inttostr(j + 1) + '=' + floatTostrF(yc[j], ffGeneral, 10, 8));
memo1.Lines.Add(' 懸垂線 直線差 ' + floatTostr(yc[j] - ys[j]));
if j = 0 then begin
memo1.Lines.Add(' a = ' + floattostr(a1));
fd := ys[0] - a1 * xs;
end
else begin
memo1.Lines.Add(' a = ' + floattostr(a2));
fd := ys[1] - a2 * xe;
end;
memo1.Lines.Add(' b = ' + floatTostr(fd));
end;
if ch = 3 then memo1.Lines.Add(' X3' + '=' + floatTostrF(x[2],ffGeneral, 10, 8) + ' 不要データー');
ch := 2;
end
else begin // 接線が無い場合のグラフ設定
xs := -C;
xe := C;
if d < xs then xs := d;
if d > xe then xe := d;
ys[0] := 0;
yc[0] := C * (cosh(xs / C) -1);
ys[1] := b;
yc[1] := C * (cosh(xe / C) -1);
end;
// グラフ表示スケール設定
if xe * xs <= 0 then yyb := 0 // xの値-x ～+x なら y値0
else begin
yyb := ys[0]; // -x-x 又は +x+x なら
fd := ys[1];
if fd < yyb then yyb := fd; // 小さい方のy値選択
end;
if ys[0] > ys[1] then yt := ys[0] // 大きい方のy値選択
else yt := ys[1];
if b < yyb then yyb := b;
if xe < xs then begin // 小さい方の値をxsに
fd := xe;
xe := xs;
xs := fd;
end;
yyt := yt; // グラフ上側の値
xxs := xs; // x方向スケール
xxe := xe;
if (xxs - xxe) < 1E-8 then begin
xxs := xxs - 0.1;
xxe := xxe + 0.1;
xs := xxs;
xe := xxe;
end;
if (xxe - xxs) > (yyt - yyb) then begin // 縦横スケール設定
fd := ((xxe - xxs) - (yyt - yyb)) / 2;
yyb := yyb - fd;
yyt := yyt + fd;
end
else begin
fd := ((yyt - yyb) - (xxe - xxs)) / 2;
xxs := xxs - fd;
xxe := xxe + fd;
end;
fd := (xxe - xxs) / 10; // グラフ余裕分設定
xxs := xxs - fd;
xxe := xxe + fd;
yyb := yyb - fd;
yyt := yyt + fd;
if checkbox1.Checked then begin
Series2.AddXY(xxs, yyt);
Series2.AddXY(xxs, yyb);
Series2.AddXY(xxe, yyb);
application.ProcessMessages; // グラフ表示待ち スケール設定
end;
// グラフ表示 カテナリー線と接線
j := 0;
try
Drawing(yyt, yyb, Ch);
except
on E: Exception do begin // オーバーフロー処理
StrText := E.ClassName + sLineBreak + E.Message;
StrText := StrText + #13#10 + 'グラフ作図ルーチン';
Application.MessageBox(PChar(StrText), '情報', MB_ICONINFORMATION);
j := 1;
end;
end;
if j = 1 then begin // オーバーフローが有ったら此処迄
Button1.Enabled := True;
exit;
end;
if ch = 2 then Series4.AddXY(x[0], ys[0]); // 接点左
Series4.AddXY(d, b); // 指定点
if ch = 2 then Series4.AddXY(x[1], ys[1]); // 接点右
Button1.Enabled := true;
end;
end.
catenary_No2_specified_point_Passing_straight_line_tangent_to_a_curve.zip