懸垂線と直線の交点
懸垂線（カテナリー曲線）と直線の交点を求めます。
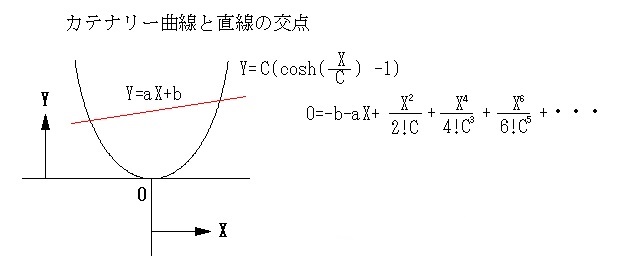カテナリー曲線と、直線の交点を求める為には、連立方程式を解く必要があります。
直線とカテナリー曲線との交点があるかどうかの判定は、その直線の傾きの接点を求めて、切片の計算をします。
与えられた直線の切片が、接線の切片より大きければ交点があることになります。
与えられた直線と平行のカテナリー曲線と接する直線は簡単に求める事ができます。
ＤＫＡ法でX座標を計算する場合は、複素数がゼロに近い値がある場合は、交点があり、無い場合は交点が無い事になります。
ＤＫＡ法を使用しない場合は、冪級数展開を四次の項迄とし、四次方程式を解いた後、交点位置への収束計算をします。
方程式の解法を使用しなくても、収束計算だけでも交点の計算は可能です。
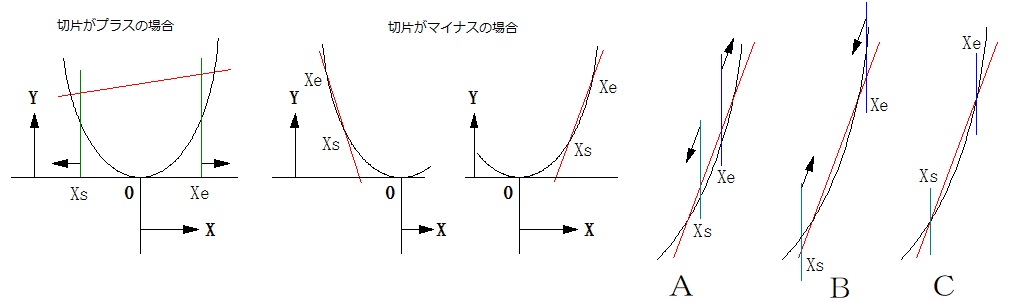
次数が低い方法で方程式を開放した場合の収束方法についてです。
与えられた直線の切片がプラスの場合は、必ず交点があり、交点が、マイナスX座標と、ブラスX座標となるので、上図一番左の図の矢印方向に収束計算を行います。
問題なのは、上図切片がマイナスの場合で、直線の傾斜によって、交点がプラス側か、マイナス側に別れます。
この時、収束計算の方向を上図のAの方向にします、Bの方向にすると、ＸｓとＸｅの値が近い場合、収束計算値が、Ｘｓの場合Xeと同じになったり飛び越えてしまったりして収束に失敗することがあります。
Xeの計算も同じことが発生します。
方程式の解法を使用しない場合は、接点の計算を行い、接点位置から、交点収束計算を行えば、簡単に交点を求める事が出来ます。
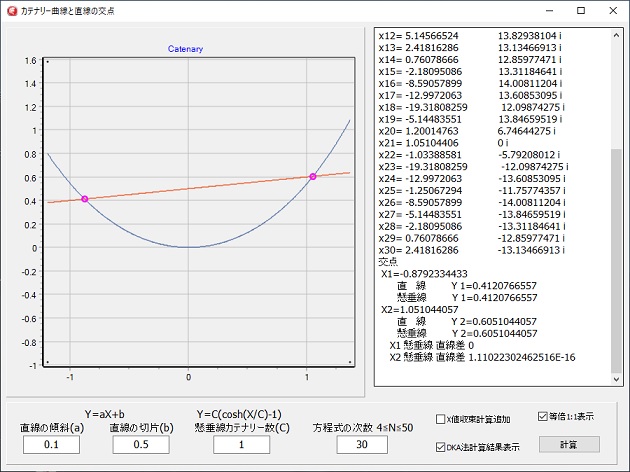左図はプログラム実行例ですが、DKA法と、DKAの次数を少なくした場合に、収束計算を行なうプ゜ログラムです。
交点は二ヶ所なので、ＤＫＡ法の次数は必ず偶数とします。
プログラム
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls,
VclTee.TeeGDIPlus, VCLTee.TeEngine, VCLTee.Series, VCLTee.TeeProcs,
VCLTee.Chart;
type
TForm1 = class(TForm)
Memo1: TMemo;
Panel1: TPanel;
a_Edit: TLabeledEdit;
b_Edit: TLabeledEdit;
C_Edit: TLabeledEdit;
Chart1: TChart;
Series1: TLineSeries;
Series2: TPointSeries;
Button1: TButton;
Series3: TLineSeries;
Label1: TLabel;
Label2: TLabel;
CheckBox1: TCheckBox;
Series4: TPointSeries;
degreeEdit: TLabeledEdit;
CheckBox2: TCheckBox;
CheckBox3: TCheckBox;
procedure Button1Click(Sender: TObject);
private
{ Private 宣言 }
function datainput: boolean;
procedure Drawing(yyt, yyb: double);
procedure dataset(n: integer;var d: array of double);
procedure convergence(var x: array of double);
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses
system.Math;
var
C : double; // カテナリー数
a : double; // 直線の傾き
b : double; // 直線の切片
deg : integer; // 方程式の次数
xs, xe: double; // X軸の範囲
yt: double; // y軸の範囲
// Durand Kerner Aberth algorithm
function dka(a : array of double; var cr, ci: array of double; n: integer): boolean;
var
r, r0, t : double;
e, f1, f2, w1, w2 : double;
p1, p2, a1, a2, norm: double;
i, j, L: integer;
ca : array of double;
zc : double;
StrText : string;
eps : double;
begin
result := true;
setlength(ca, n + 1);
for i := 0 to n do ca[i] := a[i];
zc := - ca[n-1] / n;
for i := 1 to n do
for j := n downto i do
ca[j-1] := ca[j-1] + ca[j] * zc;
r := 0;
for i := 0 to n - 1 do begin
r0 := power(n * abs(ca[i]), 1/(n-i));
if r < r0 then r := r0;
end;
eps := 1E-14 * r;
Form1.Memo1.Lines.Add('R = ' + floatTostr(R));
for i := 1 to n do begin // 半径rの円に等間隔に配置する
t := 2 * PI / n * (i - 3.0 / 4.0);
cr[i-1] := -a[n-1] / n + r * cos(t); // アーバスの初期値
ci[i-1] := r * sin(t);
end;
L := 0;
try
repeat
e := 0;
for i := 0 to n -1 do begin
f1 := 1; // 分子 f(zi)、実部=f1,虚部=f2
f2 := 0; // ※a[n]=1
for j := n-1 downto 0 do begin // ホーナー法 f(z)=( … ((z+a[n-1])*z+a[n-2])*z+a[n-3])* … +a[1])*z+a[0]
w1 := f1 * cr[i] - f2 * ci[i]; // f*z=(f1+i*f2)*(x1+i*x2)=(f1*x1-f2*x2)+i*(f1*x2+f2*x1)
w2 := f2 * cr[i] + f1 * ci[i];
f1 := w1 + a[j]; // f=z+a[j]
f2 := w2;
end;
p1 := 1; // 分母 Π[j=1,N,i≠j](zi-zj)、実部=p1,虚部=p2
p2 := 0;
for j := 0 to n - 1 do begin
if j <> i then begin
w1 := p1 * (cr[i] - cr[j]) - p2 * (ci[i] - ci[j]); // p*(zi-zj)
w2 := p1 * (ci[i] - ci[j]) + p2 * (cr[i] - cr[j]);
p1 := w1; // p=(zi-zj)
p2 := w2;
end;
end;
t := p1 * p1 + p2 * p2; // 分子÷分母 (f1+i*f2)/(p1+i*p2)=(f1+i*f2)(p1-i*p2)/(p1*p1+p2*p2)
if t = 0 then begin
application.MessageBox('０では割れません。(DKAルーチン)', '注意', 0);
result := false;
exit;
end;
a1 := (f1 * p1 + f2 * p2) / t;
a2 := (f2 * p1 - f1 * p2) / t;
norm :=sqrt(a1 * a1 + a2 * a2);
if e < norm then e := norm; // 最大値
cr[i] := cr[i] - a1; // k回目の近似根 zi[k+1]=zi[k]-f(zi[k])/Π[j=1,N,i≠j](zi[k]-zj[k])
ci[i] := ci[i] - a2;
end;
inc(L);
until (e < eps) or (L > 400);
except
on E: Exception do begin
StrText := E.ClassName + sLineBreak + E.Message;
StrText := StrText + sLineBreak + 'DKA法計算ルーチン';
StrText := StrText + sLineBreak + 'オーバーフローだったら次数を下げて計算してみてください。';
Application.MessageBox(PChar(StrText), '情報', MB_ICONINFORMATION);
result := False;
end;
end;
Form1.Memo1.Lines.Add('DKA法 Loop = ' + intTostr(L))
end;
// 入力処理
function TForm1.datainput: boolean;
var
ch: integer;
begin
result := false;
val(C_edit.Text, C, ch);
if (ch <> 0) or (C <= 0) then begin
application.MessageBox('カテナリー数に間違いがあります。','注意',0);
exit;
end;
val(a_edit.Text, a, ch);
if ch <> 0 then begin
application.MessageBox('直線の傾きに間違いがあります。','注意',0);
exit;
end;
val(b_edit.Text, b, ch);
if (ch <> 0) then begin
application.MessageBox('直線の切片に間違いがあります。','注意',0);
exit;
end;
val(degreeedit.Text, deg, ch);
if (ch <> 0) then begin
application.MessageBox('方程式の次数に間違いがあります。','注意',0);
exit;
end;
if deg > 50 then begin
application.MessageBox('方程式の次数の値が大きすぎます（５０迄）。','注意',0);
exit;
end;
if deg < 2 then begin
application.MessageBox('方程式の次数の値が小さすぎます（４以上）。','注意',0);
exit;
end;
if deg mod 2 <> 0 then begin
application.MessageBox('方程式の次数の値は偶数にして下さい。','注意',0);
exit;
end;
result := true;
end;
// 懸垂線作図
procedure TForm1.Drawing(yyt, yyb: double);
const
K = 500;
var
xn : double;
x, dx : double;
y : double;
i : integer;
begin
dx := (xe - xs) / K;
// 懸垂線作図
for i := -K div 10 to K + K div 10 do begin
xn := i * dx + xs; // 計算位置
x := abs(xn);
y := C * (cosh(x / C) - 1); // カテナリー曲線
if (y < yyt) and (y >= yyb) then Series1.AddXY(xn, y);
y := a * xn + b; // 直線
if (y < yyt) and (y >= yyb) then Series3.AddXY(xn, y);
end;
end;
// cosh 値用N次元データー作成
procedure TForm1.dataset(n: integer; var d: array of double);
var
i : integer;
function factorial(n: integer): double; // n!
var
j : integer;
begin
result := 1;
for j := 2 to n do result := result * j;
end;
begin
d[0] := -b; // 定数項
d[1] := -a; // x^1
for i := 2 to n do begin
if i mod 2 = 0 then d[i] := 1 / factorial(i) / power(C, i - 1) // x^2n偶数次数項
else d[i] := 0; // 奇数次数は 0
end;
end;
// x値収束計算
// 接線に近い場合収束出来ません
procedure TForm1.convergence(var x: array of double);
const
KM = 1E-8;
KE = 1E-13;
KL = 1000;
var
i, j : integer;
xs, xe: double;
yyt, yyb: double;
fds, fde: double;
dd, fd : double;
xxs, xxe: double;
begin
memo1.Lines.Add('収束計算指定あり');
// 接線の確認
xs := arcsinh(a) * C; // 線の傾きからX座標計算
yyt := C * (cosh(xs / C) -1); // 懸垂線のY座標
yyb := a * xs + b; // 直線のY座標
// 接線と判断したら同じ値に設定 Y 座標の差が小さければ接線と判断
if abs(yyt - yyb) < 1E-4 * a then begin
x[0] := xs;
x[1] := xs;
memo1.Lines.Add(' 接線に近いため収束計算出来ません。');
exit;
end;
// 絶対値の小さい方がxs
if abs(x[0]) < abs(x[1]) then begin
xs := x[0];
xe := x[1];
end
else begin
xs := x[1];
xe := x[0];
end;
// DKA法による結果表示
for j := 0 to 1 do begin
memo1.Lines.Add(' X' + inttostr(j + 1) + '=' + floatTostrF(x[j], ffGeneral, 10, 8)
+ ' Y' + inttostr(j + 1) + '=' + floatTostrF(x[j] * a + b, ffGeneral, 10, 8));
memo1.Lines.Add(' カテナリー Yc' +
inttostr(j + 1) + '=' + floatTostrF(C * (cosh(x[j] / C) - 1),ffGeneral, 10, 8));
end;
yyt := C * (cosh(xs / C) -1);
yyb := a * xs + b;
fds := yyt - yyb;
memo1.Lines.Add(' XsY誤差 ' + floatTostr(fds));
yyt := C * (cosh(xe / C) -1);
yyb := a * xe + b;
fde := yyt - yyb;
memo1.Lines.Add(' XeY誤差 ' + floatTostr(fde));
// Ｘｓによるｙ誤差が＋だったら誤差をマイナスにします
i := 0;
fd := abs(xe - xs) / 100;
if fds > KM then begin // xs
if xs * xe > 0 then begin
dd := fd;
repeat
if xs < 0 then xs := xs - dd
else xs := xs + dd;
yyt := C * (cosh(xs / C) -1);
yyb := a * xs + b;
inc(i);
until (yyt - yyb <= 0) or (i > KL);
end
else begin
dd := -xs / 200;
repeat
xs := xs + dd;
yyt := C * (cosh(xs / C) -1);
yyb := a * xs + b;
inc(i);
until ((yyt - yyb) <= 0) or (i > KL);
end;
fds := yyt - yyb;
end;
if i = 0 then memo1.Lines.Add(' LoopDef Xs = ' + intTostr(i))
else memo1.Lines.Add(' LoopDef Xs = ' + intTostr(i) + ' 誤差 ' + floatTostr(fds));
// Ｘｅによるｙ誤差が＋だったら誤差をマイナスにします
i := 0;
if fde > KM then begin // xe
if xs * xe > 0 then begin
dd := fd;
repeat
if xe < 0 then xe := xe + dd
else xe := xe - dd;
yyt := C * (cosh(xe / C) -1);
yyb := a * xe + b;
inc(i);
until (yyt - yyb <= 0) or (i > KL);
end
else begin
dd := xe / 200;
repeat
xe := xe - dd;
yyt := C * (cosh(xe / C) -1);
yyb := a * xe + b;
inc(i);
until (yyt - yyb <= 0) or (i > KL);
end;
fde := yyt - yyb;
end;
if i = 0 then memo1.Lines.Add(' LoopDef Xe = ' + intTostr(i))
else memo1.Lines.Add(' LoopDef Xe = ' + intTostr(i) + ' 誤差 ' + floatTostr(fde));
// 誤差が大きい時交点再計算 xs 誤差の値が-でないと計算出来ません
xxs := xs;
yyt := a * xs + b;
yyb := C * (cosh(xs / C) - 1);
fd := yyt - yyb;
i := 0;
if abs(fd) > Km then begin
fd := xs / 2;
if xe * xs > 0 then fd := -fd; // xの符号によって補正値符号設定
repeat
xxs := xxs + fd;
yyt := a * xxs + b;
yyb := C * (cosh(abs(xxs) / C) - 1);
if yyt < yyb then begin
xxs := xxs - fd;
fd := fd / 4;
end;
inc(i);
until (abs(fd) < kE) or (i > KL);
xs := xxs;
end;
memo1.Lines.Add('収束 Loop数 xs= ' + inttostr(i));
// 誤差が大きい時交点再計算 xe 誤差の値が-でないと計算出来ません
xxe := xe;
yyt := a * xe + b;
yyb := C * (cosh(xe / C) - 1);
fd := yyt - yyb;
i := 0;
if abs(fd) > Km then begin
fd := xe / 2;
repeat
xxe := xxe + fd;
yyt := a * xxe + b;
yyb := C * (cosh(abs(xxe) / C) - 1);
if yyt < yyb then begin
xxe := xxe - fd;
fd := fd / 4;
end;
inc(i);
until (abs(fd) < KE) or (i > KL);
xe := xxe;
end;
memo1.Lines.Add('収束 Loop数 xe= ' + inttostr(i));
x[0] := xs;
x[1] := xe;
end;
// カテナリー線と直線の交点計算の実行
procedure TForm1.Button1Click(Sender: TObject);
var
ab : array of double;
cr : array of double;
ci : array of double;
i, n, j, ch: integer;
fd : double;
fds, fde: double;
li : int64;
scou : string;
x : array of double;
ys : array of double;
yc : array of double;
xxs, xxe: double;
yyb, yyt: double;
StrText : string;
procedure roundfd(var d: double);
begin
if abs(d) < 1E5 then begin
li := round(d * 1E8); // 小数点8桁以下丸め
d := li / 1E8;
end;
end;
begin
xs := -1;
xe := 1;
// データー入力処理
if not datainput then exit;
Button1.Enabled := False;
n := deg;
// 次数で配列の確保
setlength(ab, n + 1);
setlength(cr, n);
setlength(ci, n);
setlength(x, 2);
setlength(ys, 2);
setlength(yc, 2);
// 配列にデーターセット
dataset(n, ab);
j := 0;
// 配列先頭の値を１に設定
try
for i := n-1 downto 0 do begin
ab[i] := ab[i] / ab[n];
end;
except
on E: Exception do begin
StrText := E.ClassName + sLineBreak + E.Message;
StrText := StrText + sLineBreak + '配列の先頭を１にする処理';
Application.MessageBox(PChar(StrText), '情報', MB_ICONINFORMATION);
j := 1;
end;
end;
if j = 1 then begin
Button1.Enabled := True;
exit;
end;
ab[n] := 1;
memo1.Clear;
Series1.Clear;
Series2.Clear;
Series3.Clear;
Series4.Clear;
application.ProcessMessages;
memo1.Lines.Add('DKA法 次数 = ' + intTostr(n));
// dka法 計算
if not dka(ab, cr, ci, n) then begin
Button1.Enabled := true;
exit;
end;
// dka法 答え表示
if checkbox2.Checked then
for i := 0 to n-1 do begin
fd := cr[i]; // 実数部
roundfd(fd); // 小数点8桁以下丸め
scou := 'x' + inttostr(i + 1) + '= ' + floatTostr(fd);
ch := length(scou);
ch := 28 - ch;
for j := 0 to ch do scou := scou + ' ';
fd := ci[i]; // 虚数部
roundfd(fd); // 小数点8桁以下丸め
memo1.Lines.Add(scou + floatTostr(fd) + ' i');
end;
// 交点の検出 虚数が小さい場所
j := 0;
for i := 0 to n-1 do begin
if abs(ci[i]) < 1E-8 then begin
fd := cr[i];
if j <= 1 then begin
x[j] := fd;
end;
inc(j);
end;
end;
if j = 0 then begin
memo1.Lines.Add('');
memo1.Lines.Add('交点を検出できませんでした。');
button1.Enabled := true;
exit;
end;
if j = 1 then begin
memo1.Lines.Add('');
memo1.Lines.Add('交点を分離できませんでした。');
button1.Enabled := true;
exit;
end;
if j > 2 then begin
memo1.Lines.Add('');
memo1.Lines.Add('交点を正しく検出できませんでした。');
button1.Enabled := true;
exit;
end;
// x値収束計算
if checkbox3.Checked then convergence(x);
memo1.Lines.Add('交点');
xs := x[0];
xe := x[1];
ys[0] := a * xs + b;
yc[0] := C * (cosh(xs / C) -1);
ys[1] := a * xe + b;
yc[1] := C * (cosh(xe / C) -1);
// 結果表示表示
for j := 0 to 1 do begin
memo1.Lines.Add(' X' + inttostr(j + 1) + '=' + floatTostrF(x[j],ffGeneral, 10, 8));
memo1.Lines.Add(' 直 線 Y ' + inttostr(j + 1) + '=' + floatTostrF(ys[j], ffGeneral, 10, 8));
memo1.Lines.Add(' 懸垂線 Y ' + inttostr(j + 1) + '=' + floatTostrF(yc[j], ffGeneral, 10, 8));
end;
yyt := yc[0];
yyb := ys[0];
fds := yyt - yyb;
memo1.Lines.Add(' X1 懸垂線 直線差 ' + floatTostr(fds));
yyt := yc[1];
yyb := ys[1];
fde := yyt - yyb;
memo1.Lines.Add(' X2 懸垂線 直線差 ' + floatTostr(fde));
// グラフ表示スケール設定
if xe * xs <= 0 then yyb := 0 // xの値-x ～+x なら y値0
else begin
yyb := ys[0]; // -x-x 又は +x+x なら
fd := ys[1];
if fd < yyb then yyb := fd; // 小さい方のy値選択
end;
if ys[0] > ys[1] then yt := ys[0] // 大きい方のy値選択
else yt := ys[1];
if xe < xs then begin // 小さい方の値をxsに
fd := xe;
xe := xs;
xs := fd;
end;
yyt := yt; // グラフ上側の値
xxs := xs; // x方向スケール
xxe := xe;
if (xxs - xxe) < 1E-8 then begin
xxs := xxs - 0.1;
xxe := xxe + 0.1;
xs := xxs;
xe := xxe;
end;
if (xxe - xxs) > (yyt - yyb) then begin // 縦横スケール設定
fd := ((xxe - xxs) - (yyt - yyb)) / 2;
yyb := yyb - fd;
yyt := yyt + fd;
end
else begin
fd := ((yyt - yyb) - (xxe - xxs)) / 2;
xxs := xxs - fd;
xxe := xxe + fd;
end;
fd := (xxe - xxs) / 10; // グラフ余裕分設定
xxs := xxs - fd;
xxe := xxe + fd;
yyb := yyb - fd;
yyt := yyt + fd;
if checkbox1.Checked then begin
Series2.AddXY(xxs, yyt);
Series2.AddXY(xxs, yyb);
Series2.AddXY(xxe, yyb);
application.ProcessMessages;
end;
// グラフ表示
Drawing(yyt, yyb);
Series4.AddXY(x[0], ys[0]);
Series4.AddXY(x[1], ys[1]);
Button1.Enabled := true;
end;
end.
catenary_intersection.zip