unit Unit1;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, VclTee.TeeGDIPlus,
VCLTee.TeEngine, VCLTee.Series, Vcl.ExtCtrls, VCLTee.TeeProcs, VCLTee.Chart;
type
TForm1 = class(TForm)
Memo1: TMemo;
Chart1: TChart;
Series1: TFastLineSeries;
Series2: TFastLineSeries;
GroupBox1: TGroupBox;
RadioButton2: TRadioButton;
Button1: TButton;
RadioButton1: TRadioButton;
GroupBox2: TGroupBox;
Button2: TButton;
Label1: TLabel;
Label2: TLabel;
procedure Button1Click(Sender: TObject);
procedure Button2Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
{
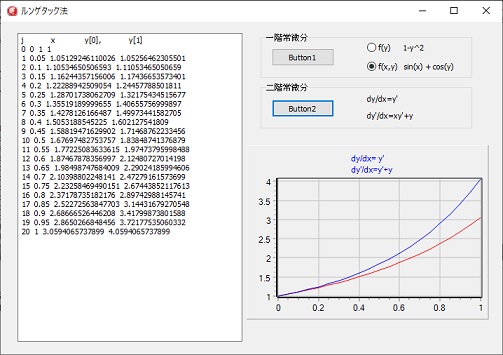
4次のルンゲタック法
一階の常微分方程式
dy/dx=f(x,y)
}
function f(x, y: double):double;
begin
result := 1; // ダミー
if Form1.RadioButton2.Checked then result := sin(x) + cos(y);
if Form1.RadioButton1.Checked then result := 1 - y * y; // x は無視
end;
procedure sumple1;
var
i : integer;
h, x, y, k1, k2, k3, k4: double;
begin
h := 1; // 分割幅 ダミー
if Form1.RadioButton2.Checked then begin
h := pi / 50; // 0～π迄微分
Form1.Chart1.Title.Text.Text := 'sin(x) + cos(y)';
end;
if Form1.RadioButton1.Checked then begin
h := 1 / 50; // 0～1迄微分
Form1.Chart1.Title.Text.Text := '1-y^2';
end;
x := 0;
y := 0;
i := 0;
with Form1.memo1 do begin
clear;
Form1.Series1.Clear;
Form1.Series2.Clear;
Lines.Add('i x y');
Lines.Add(inttostr(i) + ' ' + floatTostr(x) + ' ' + floatTostr(y));
Form1.Series1.AddXY(x, y);
for i := 1 to 50 do begin
k1 := h * f(x, y);
k2 := h * f(x + h / 2, y + k1 / 2);
k3 := h * f(x + h / 2, y + k2 / 2);
k4 := h * f(x + h, y + k3);
y := y + (k1 + 2 * k2 + 2 * k3 + k4) / 6; // 重み付き平均
x := i * h;
Lines.Add(inttostr(i) + ' ' + floatTostr(x) + ' ' + floatTostr(y));
Form1.Series1.AddXY(x, y);
end;
end;
end;
// 一階常微分実行
procedure TForm1.Button1Click(Sender: TObject);
begin
sumple1;
end;
{
二階常微分方程式
d^2/dx^2=x*dy/dx+y
dy/dx=y' -------(a)
dy'/dx=xy'+y ---(b)
}
function df(i:integer; x: double; s: array of double): double;
begin
{
i=0 dy/dx=y'
i=1 dy'/dx=xy'+y
}
result := 0;
case i of
0 : result := s[1];
1 : result := x * s[1] + s[0];
end;
end;
procedure sumple2;
var
j, k: integer;
h, x: double;
k1, k2, k3, k4, y, ywork: array[0..1] of double;
begin
k := 20;
h := 1 / k;
x := 0;
y[0] := 1;
y[1] := 1;
j := 0;
with Form1 do begin
Memo1.clear;
Chart1.Title.Text.Text := 'dy/dx= y' + #39 + #13#10 + ' dy' + #39 + '/dx=y' + #39 + '+y';
Series1.Clear;
Series2.Clear;
Memo1.Lines.Add('j x y[0], y[1]');
Memo1.Lines.Add(inttostr(j) + ' ' + floatTostr(x) + ' ' + floatTostr(y[0]) + ' ' + floatTostr(y[1]));
Series1.addxy(x, y[0]);
Series2.addxy(x, y[1]);
for j := 1 to k do begin
k1[0] := h * df(0, x, y);
k1[1] := h * df(1, x, y);
ywork[0] := y[0] + k1[0] / 2;
ywork[1] := y[1] + k1[1] / 2;
k2[0] := h * df(0, x + h / 2, ywork); // k2[0] := h * ywork[1]
k2[1] := h * df(1, x + h / 2, ywork);
ywork[0] := y[0] + k2[0] / 2;
ywork[1] := y[1] + k2[1] / 2;
k3[0] := h * df(0, x + h / 2, ywork); // k3[0] := h * ywork[1]
k3[1] := h * df(1, x + h / 2, ywork);
ywork[0] := y[0] + k3[0];
ywork[1] := y[1] + k3[1];
k4[0] := h * df(0, x + h, ywork); // k4[0] := h * ywork[1]
k4[1] := h * df(1, x + h, ywork);
y[0] := y[0] + (k1[0] + 2 * k2[0] + 2 * k3[0] + k4[0]) / 6;
y[1] := y[1] + (k1[1] + 2 * k2[1] + 2 * k3[1] + k4[1]) / 6;
x := h * j;
Memo1.Lines.Add(inttostr(j) + ' ' + floatTostr(x) + ' ' + floatTostr(y[0]) + ' ' + floatTostr(y[1]));
Series1.addxy(x, y[0]);
Series2.addxy(x, y[1]);
end;
end;
end;
// 二階常微分実行
procedure TForm1.Button2Click(Sender: TObject);
begin
sumple2;
end;
end.
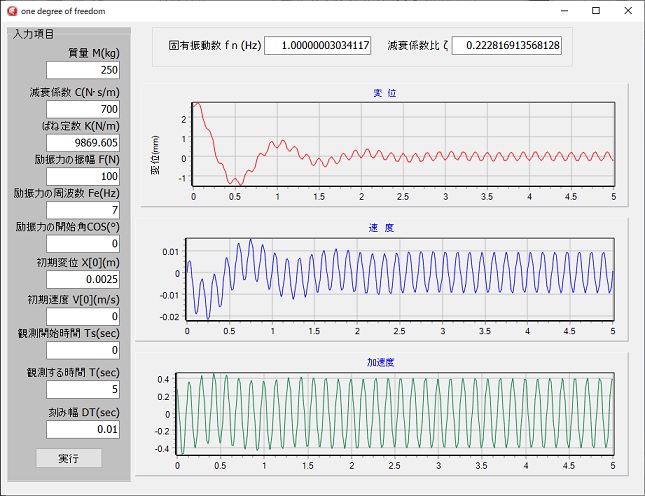左図は、減衰振動と強制振動のプログラムの実行例です。
減衰と強制振動を同時に与えています。
減衰 強制
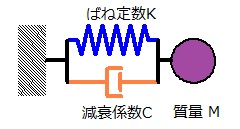
d2x/dt2 = -ω02x - 2γdx/dt + F0cosωt
質量 Kg
減衰係数 N・s/m
ばね定数 N/m
励振力の振幅 N
励振力の周波数 Hz
励振力の開始角 deg (開始する角度によって初期振動が変かします。)
初期変位 m (質量Mの最初の位置です)
初期速度 m/s
観測開始時間 sec
観測する時間 sec
刻み幅 sec (dtの時間です)
x (位置、変位)
dx/dt = v(速度) 位置の変化量を時間で微分すれば速度になります。
dv/dt = α(加速度) 更に速度の変化を時間で微分すれば加速度になります。
// 一自由度系の振動 // 四次のルンゲクッタ法 unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls, VclTee.TeeGDIPlus, VCLTee.TeEngine, VCLTee.Series, VCLTee.TeeProcs, VCLTee.Chart; type TForm1 = class(TForm) GroupBox1: TGroupBox; LabeledEdit1: TLabeledEdit; LabeledEdit2: TLabeledEdit; LabeledEdit3: TLabeledEdit; LabeledEdit4: TLabeledEdit; LabeledEdit5: TLabeledEdit; LabeledEdit6: TLabeledEdit; LabeledEdit7: TLabeledEdit; LabeledEdit8: TLabeledEdit; LabeledEdit9: TLabeledEdit; Button1: TButton; GroupBox2: TGroupBox; Label1: TLabel; Edit1: TEdit; Label2: TLabel; Edit2: TEdit; Chart1: TChart; Series1: TFastLineSeries; Chart2: TChart; Series2: TFastLineSeries; Chart3: TChart; Series3: TFastLineSeries; LabeledEdit10: TLabeledEdit; LabeledEdit11: TLabeledEdit; procedure Button1Click(Sender: TObject); private { Private 宣言 } function hzcalc: boolean; function inputdata: boolean; function Func(T: double; X: array of double): double; procedure Runge_Kutta(T, Dt: double;var X, Y: array of double); procedure calc; public { Public 宣言 } end; var Form1: TForm1; implementation {$R *.dfm} var dblAK, dblAC : double; dblb : double; Omega, OmegQ : double; dblM, dblC, dblK : double; dblF, dblFe : double; dblQ : double; dblX0, dblV0 : double; dblT, dblTstt, dblTend, dblDt : double; dblX, dblY : array[0..1] of double; Number, Numbstt : integer; // 固有周波数 減衰係数の処理 function TForm1.hzcalc: boolean; var Check : integer; begin result := false; val(LabeledEdit1.Text, dblM, Check); // Kg if Check <> 0 then begin application.MessageBox('質量の値に間違いがあります。','注意',0); exit; end; val(LabeledEdit2.Text, dblC, Check); // N・s/m if Check <> 0 then begin application.MessageBox('減衰係数の値に間違いがあります。','注意',0); exit; end; val(LabeledEdit3.Text, dblK, Check); // N/m if Check <> 0 then begin application.MessageBox('ばね定数の値に間違いがあります。','注意',0); exit; end; if dblK <= 0 then begin application.MessageBox('ばね定数の値がゼロ又は、ゼロ以下です。','注意',0); exit; end; if dblM <= 0 then begin application.MessageBox('質量の値がゼロ又は。ゼロ以下ではいけません。','注意',0); exit; end; // 固有周波数 Hz dblF := sqrt(dblK / dblM) / 2 / pi; // 減衰係数比 ζ dblFe := dblC / 2 / sqrt(dblM * dblK); Edit1.Text := floattostr(dblF); Edit2.Text := floattostr(dblFe); result := True; end; // 入力データー処理 function TForm1.inputdata: boolean; var check : integer; begin result := false; val(LabeledEdit4.Text, dblF, Check); // N if Check <> 0 then begin application.MessageBox('励震力の振幅の値に間違いがあります。','注意',0); exit; end; val(LabeledEdit5.Text, dblFe, Check); // Hz if (Check <> 0) or (dblFe < 0) then begin application.MessageBox('励震力の周波数の値に間違いがあります。','注意',0); exit; end; val(LabeledEdit10.Text, dblQ, Check); // deg if Check <> 0 then begin application.MessageBox('励震力の開始角の値に間違いがあります。','注意',0); exit; end; val(LabeledEdit6.Text, dblX0, Check); // m(メートル) if Check <> 0 then begin application.MessageBox('初期変位の値に間違いがあります。','注意',0); exit; end; val(LabeledEdit7.Text, dblV0, Check); // m/s if Check <> 0 then begin application.MessageBox('初期速度の値に間違いがあります。','注意',0); exit; end; val(LabeledEdit8.Text, dblTend, Check); // sec if (Check <> 0) or (dblTend <= 0) then begin application.MessageBox('観測する時間に間違いがあります。','注意',0); exit; end; val(LabeledEdit11.Text, dblTstt, Check); // sec if (Check <> 0) or (dblTstt < 0) then begin application.MessageBox('観測開始時間に間違いがあります。','注意',0); exit; end; val(LabeledEdit9.Text, dblDt, Check); // sec if (Check <> 0) then begin application.MessageBox('刻み幅に間違いがあります。','注意',0); exit; end; if dblDt <= 0 then begin application.MessageBox('刻み幅がゼロ 又は、ゼロ以下ではいけません。','注意',0); exit; end; // 励震力の角周波数ω Omega := 2 * pi * dblFe; // 励震力の開始角 OmegQ := dblQ / 180 * pi; // 計算データー数 - 1 Number := round((dblTend + dblTstt) / dblDt); // 観測開始位置 Numbstt := round((dblTstt) / dblDt) + 1; dblAK := -dblK / dblM; dblAC := -dblC / dblM; dblB := dblF / dblM; result := true; end; // 加速度を求めます // 速度分無はルーチン内で処理 function TForm1.Func(T: double; X: array of double): double; begin result := dblAK * X[0] + dblAC * X[1] + dblB * cos(Omega * T + OmegQ); end; // ルンゲクッタルーチン procedure TForm1.Runge_Kutta(T, Dt: double;var X, Y: array of double); var Rk1: array[0..1] of double; Rk2: array[0..1] of double; Rk3: array[0..1] of double; Rk4: array[0..1] of double; Acc: array[0..1] of double; Dt2: double; Th2, Th: double; begin Dt2 := Dt / 2; Th2 := T + Dt2; Th := T + Dt; Rk1[0] := X[1]; Rk1[1] := Func(T, X); Acc[0] := X[0] + Rk1[0] * Dt2; Acc[1] := X[1] + Rk1[1] * Dt2; Rk2[0] := Acc[1]; Rk2[1] := Func(Th2, Acc); Acc[0] := X[0] + Rk2[0] * Dt2; Acc[1] := X[1] + Rk2[1] * Dt2; Rk3[0] := Acc[1]; Rk3[1] := Func(Th2, Acc); Acc[0] := X[0] + Rk3[0] * Dt; Acc[1] := X[1] + Rk3[1] * Dt; Rk4[0] := Acc[1]; Rk4[1] := Func(Th, Acc); Y[0] := (Rk1[0] + 2 * (Rk2[0] + Rk3[0]) + Rk4[0]) / 6; // 区間重み付き平均速度 Y[1] := (Rk1[1] + 2 * (Rk2[1] + Rk3[1]) + Rk4[1]) / 6; // 区間重み付き平均加速度 // 変位 + 区間重み付き平均速度 x Δ時間 X[0] := X[0] + Y[0] * Dt; // 変位 // 速度 + 区間重み付き平均加速度 x Δ時間 X[1] := X[1] + Y[1] * Dt; // 速度 end; // 固有振動の計算 procedure TForm1.calc; const thousand = 1000; var i : integer; begin chart1.LeftAxis.Title.Text := '変位(mm)'; Series1.Clear; Series2.Clear; Series3.Clear; dblT := 0; // 時間 dblY[0] := 0; // 区間平均速度 dblY[1] := 0; // 区間平均加速度 dblX[0] := dblX0; // 変位 dblX[1] := dblV0; // 速度 for i := 1 to Numbstt - 1 do begin // 観測開始時間まで進める Runge_Kutta(dblT, dblDt, dblX, dblY); dblT := i * dblDt; end; Series1.AddXY(dblT, dblX[0] * thousand); // 変位 Series2.AddXY(dblT, dblX[1]); // 速度 for i := Numbstt to Number do begin // 観測 Runge_Kutta(dblT, dblDt, dblX, dblY); dblT := i * dblDt; Series1.AddXY(dblT, dblX[0] * thousand); // 変位 Series2.AddXY(dblT, dblX[1]); // 速度 Series3.AddXY(dblT - dblDt, dblY[1]); // 加速度 end; Runge_Kutta(dblT, dblDt, dblX, dblY); Series3.AddXY(dblT, dblY[1]); // 加速度 end; procedure TForm1.Button1Click(Sender: TObject); begin if not hzcalc then exit; if not inputdata then exit; calc; end; end.
Runge_Kutta.zip
各種プログラム計算例に戻る