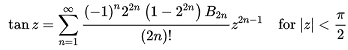
tangent function
tangent(タンジェント) 関数は、sin、cosと違って、マクローリン級数でベルヌーイ数を使用し計算が複雑になるので、tan(z)
=sin(z)/cos(z)で計算していますが、一応プログラムを作成してみました。
sin或いはcosが計算できれば、tanの計算が出来ますが、角度が0°か90°に近いとき誤差が大きくなる様です。
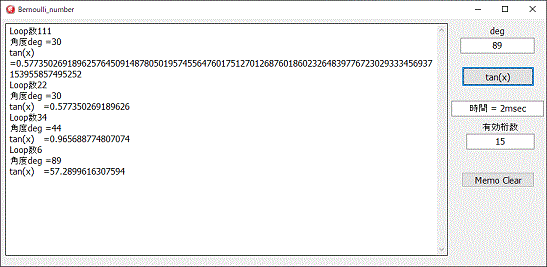プログラムは、多倍長演算で作成しました。
理由は、有効桁巣数が十数桁でも、ベルヌーイ数の値が非常に大きくなる為です。
上記の計算式で角度zが、π/2の値に近づくと、演算のループ数がどんどん増え、ベルヌーイ数が非常に大きくなり、異常に演算時間が増えます。
そこで、45°超えたら角度を対角のπ/2-zとして、答えを逆数とにして、ベルヌーイ数が大きくなるのを防止しています。
それでも、有効桁数、数百桁の計算をすると、分単位の時間がかかります。
tan=sin/cosで計算すると数秒で計算できるので、ベルヌーイ数を使用した計算は実用にはなりません。
有効桁数が15～20桁程度に固定されているのであれば、予め、ベルヌーイ数のテーブルを作成して置けば演算時間を早く出来ます。
プログラムの中で、ベルヌーイ数の計算で最大公約数を求める計算がありますが、省略しても１割程度しか早くなりません。
プログラム
unit main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.Buttons, system.Diagnostics,
Vcl.ExtCtrls, system.UITypes;
type
TForm1 = class(TForm)
Memo1: TMemo;
Edit1: TEdit;
tanX: TBitBtn;
LabeledEdit1: TLabeledEdit;
Clearbtn: TBitBtn;
LabeledEdit2: TLabeledEdit;
procedure tanXClick(Sender: TObject);
procedure ClearbtnClick(Sender: TObject);
private
{ Private 宣言 }
function incheck(s, m: string): boolean;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses Velthuis.BigIntegers, Velthuis.Bigdecimals;
var
t : array of biginteger;
// πの値
function big_pi(pcs: integer): Bigdecimal;
var
n, dpcs, pcsBack : integer;
rmback : BigDecimal.RoundingMode;
SQRT_SQRT_EPSILON, c, b, e : BigDecimal;
npow : Bigdecimal;
a, one, two, four, five, eight : Bigdecimal;
begin
pcsBack := BigDecimal.DefaultPrecision; // 除算演算精度バックアップ
rmBack := BigDecimal.DefaultRoundingMode; // 除算丸めモードバックアップ
dpcs := pcs + 5; // 指定精度 + α
BigDecimal.DefaultPrecision := dpcs;
BigDecimal.DefaultRoundingMode := rmNearesteven;
one := '1';
one := one.RoundToPrecision(dpcs); // oneの有効桁数をdpcsに設定
two := '2';
four := '4';
five := '5';
eight := '8';
SQRT_SQRT_EPSILON := one / BigDecimal.IntPower(two, pcs shl 0); // 収束判定値
c := BigDecimal.Sqrt(one / eight, dpcs * 2);
a := one + c + c + c;
b := BigDecimal.Sqrt(a, dpcs * 2);
e := b - five / eight;
b := b + b;
c := e - c;
a := a + e;
npow := '4';
n := 0;
while e > SQRT_SQRT_EPSILON do begin
npow := npow + npow;
e := (a + b) / two; // 平均値 除算有効桁数での丸め
b := a * b;
b := b.RoundToPrecision(dpcs); // pcs + α 丸め
b := BigDecimal.Sqrt(b, dpcs * 2); // 平方根有効桁数での丸め
e := e - b;
b := b + b;
c := c - e;
a := e + b;
inc(n);
end;
e := e * e;
e := e.RoundToPrecision(dpcs); // pcs + α 丸め
e := e / four; // e = e + e / 4
a := a + b;
result := (a * a - e - e / two) / (a * c - e) / npow; // 除算の順番に注意
result := result.RoundToPrecision(pcs); // 指定の精度に丸め
BigDecimal.DefaultPrecision := pcsBack; // 除算演算精度復帰
BigDecimal.DefaultRoundingMode := rmBack; // 除算丸めモード復帰
// Form1.Memo1.Lines.Append('T.Ooura Big n = ' + intTostr(n));
end;
// tan(x)
// 級数展開による計算 ベルヌーイ数使用
// -π/2 < x < π/2
function tan_Big(x: bigdecimal): bigdecimal;
var
// t : array of biginteger;
// k, nr, dpcs : integer;
n, k, nr, dpcs, dpcsb: integer;
b1, b2, q, g : biginteger;
a2, c, d, dd, e, one, two : biginteger;
s, sb, z, zz, az, m, seven : Bigdecimal;
mf, pib, pi2, pis2, onef, x9, pi9: bigdecimal;
flg : boolean;
// ベルヌーイ値表示
procedure memoout;
var
bstr : string;
begin
if b1 < 0 then bstr := ' = '
else bstr := ' = ';
Form1.memo1.Lines.Append('B' + intTostr(n) + bstr + b1.ToString +' / ' + b2.ToString);
end;
// 最大公約数 ユークリッドの互除法
function gcd_int(x, y: biginteger): biginteger;
var
t : biginteger;
begin
while y <> 0 do begin
t := x mod y;
x := y;
y := t;
end;
result := x;
end;
// Tnの値をBn値に変換表示
procedure TntoBn;
begin
b1 := n * t[0]; // 分子 n * Tn
q := q shl 2; // 分母 2^n q = q * 4
b2 := q * (q - one); // 〃 4^n - 2^n
g := gcd_int(b1, b2); // 最大公約数
b1 := b1 div g;
b2 := b2 div g;
if n mod 4 = 0 then b1 := - b1; // 符号設定
// memoout; // 値表示
end;
// kによるベルヌーイ数計算 k = 2～
procedure Bernoulli_number;
var
j: integer;
begin
// Seidel's algorithm for Tn Bn値をt[0]としたベルヌーイ計算ループ B2～
setlength(t, (k - 1) * 2 - 1); // 配列確保 追加配列クリア
if k > 2 then begin
for j := 0 to n - 2 do t[j + 1] := t[j] + t[j + 1]; // ->
t[n] := t[n - 1];
for j := n - 2 downto 0 do t[j + 1] := t[j] + t[j + 2]; // <-
t[0] := t[1];
end
else begin
t[0] := '1'; // 分子係数初期値
q := '1'; // 分母係数初期値
end ;
n := k * 2 - 2; // nの値設定
TntoBn;
end;
begin
dpcsb := Bigdecimal.DefaultPrecision;
dpcs := dpcsb + 5;
Bigdecimal.DefaultPrecision := dpcs;
seven := '0.786'; // >45°π/4=0.78539816
one := '1';
two := '2';
pib := big_pi(dpcs);
pi2 := pib + pib;
pis2 := pib / Two;
repeat // 0～2π(0～360°)の範囲に修正
if x < 0 then x := x + pi2;
if x >= pi2 then x := x - pi2;
until (x < pi2) and (x >= 0);
flg := true; // 正数フラグセット
if (x > pis2) and (x < pib) then begin // π2～π 90°～180°
x := pib - x; // 0～π/2(0～90°)の範囲に修正
flg := false // 負数フラグ設定
end;
if (x >= pib) and (x < pib + pis2) then // π～π+π/2 180°～270
x := x - pib; // 0～π/2(0～90°)の範囲に修正
if (x >= pib + pis2) and (x < pi2) then begin // π+π/2～2π 270°～360°
x := pi2 - x; // 0～π/4(0～90°)の範囲に修正
flg := false // 負数フラグ設定
end;
x9 := x.RoundToPrecision(dpcsb); // 角度指定の桁数に丸め
pi9 := pis2.RoundToPrecision(dpcsb); // rad(90°)指定の桁数に丸め
if x9 = pi9 then begin // 90°の場合
application.MessageBox('ゼロで除算、無効な値です','注意',0);
result := 0;
exit
end;
z := x;
if x > seven then begin // 0.786(45°)を超えたら対角計算
z := pib / two - z;
end;
c := 1;
d := 1;
e := 1;
dd := '4'; // 2^2
s := '0'; // Σ=0
az := z; // z
zz := z * z; // z^2
nr := 1; // n = 1 ～
repeat
sb := s; // 収束判定用 sb
k := nr + 1; // 2～ ベルヌーイ数計算用
Bernoulli_number; // ベルヌーイ数計算B(2n) b1 / b2
a2 := nr * two; // 2n
c := (a2 - one) * c * a2; // (2n)!
d := -d * dd; // -1^n * 2^2n
e := e * dd; // 2^2n
m := (one - e) * d * b1; // 整数のみまとめて積算
mf := az * m; // 浮動小数点 * 整数
mf := mf.RoundToPrecision(dpcs); // 次の除算の為の有効桁数丸め
a2 := c * b2; // 整数 * 整数
mf := mf / a2; // 浮動小数点 / 整数
s := s + mf; // Σ
s := s.RoundToPrecision(dpcs); // 収束判定の為の有効桁数丸め
az := az * zz; // z^2n-1
inc(nr); // n = n + 1
until sb = s;
form1.Memo1.Lines.Append('Loop数' + intTostr(nr - 1));
// form1.Memo1.Lines.Append(s.ToPlainString);
if x > seven then begin
onef := '1';
onef := onef.RoundToPrecision(dpcs);
s := onef / s; // 0.786(45°)を超えていたら対角
end;
if not flg then s := -s;
Bigdecimal.DefaultPrecision := dpcsb;
s := s.RoundToPrecision(dpcsb);
s := s.RemoveTrailingZeros(0);
result := s;
end;
// 入力確認
function TForm1.incheck(s, m: string): boolean;
const
ec = 'e';
eo = 'E';
dt = '.';
var
fs, es, ms : string;
ch, p, po, leng : integer;
a : double;
begin
result := false;
p := pos(ec, s); // 'e' の位置
po := pos(eo, s); // 'E' の位置
p := p + po;
if p = 0 then begin // 'e' 'E' が無かったら
val(s, a, ch);
if ch <> 0 then begin
ms := m + ' 入力値に間違いがあります。';
application.MessageBox(pchar(ms),'注意',0);
exit;
end;
result := true;
exit;
end;
leng := length(s);
fs := '';
fs := copy(s, 1, p - 1); // 'e'の前の文字取り出し
es := '';
es := copy(s, p + 1, leng - p); // 'e'の後ろの文字取り出し
val(fs, a, ch);
if ch <> 0 then begin // 'e'の前の文字の確認
ms := m + ' 入力値に間違いがあります。';
application.MessageBox(pchar(ms),'注意',0);
exit;
end;
if es <> '' then begin // 'e'の後ろの文字確認
p := pos(ec, es);
po := pos(eo, es);
p := p + po;
po := pos(dt, es);
p := p + po;
if p <> 0 then begin // 'e','E' '.',が゛有ったら
ms := m + ' 入力値に間違いがあります。';
application.MessageBox(pchar(ms),'注意',0);
exit;
end;
val(es, a, ch);
if ch <> 0 then begin
ms := m + ' 入力値に間違いがあります。';
application.MessageBox(pchar(ms),'注意',0);
exit;
end;
end;
result := true;
end;
procedure TForm1.tanXClick(Sender: TObject);
var
deg, rad, ans, D180, dega : bigdecimal;
dpcs, back, ch : integer;
StopWatch : TStopwatch;
ElapsedMillseconds : Int64;
rmback : BigDecimal.RoundingMode;
begin
// 入力チェック
if not incheck(LabeledEdit1.Text, '角度の') then exit;
val(LabeledEdit2.Text, dpcs, ch);
if ch <> 0 then begin
application.MessageBox('有効桁数に間違いがあります', '注意', 0);
exit;
end;
deg := LabeledEdit1.Text;
dega := dega.Abs(deg);
if dpcs > 1000 then begin
application.MessageBox('有効桁数が大きすぎます。','注意',0);
exit;
end;
if (dpcs >= 500) and (dega > 10) and (dega < 75) then begin
if MessageDlg('有効桁数が大きく非常に時間が掛かりますこのまま続行しますか？',
mtCustom, [mbOK,mbCancel], 0, mbCancel) = mrCancel then Exit;
end;
if (dpcs < 500) and (dpcs >= 300) and (dega > 10) and (dega < 75) then begin
if MessageDlg('時間が掛かりますこのまま続行しますか？',
mtCustom, [mbOK,mbCancel], 0, mbCancel) = mrCancel then Exit;
end;
Form1.Edit1.text := '計算中';
application.ProcessMessages;
back := Bigdecimal.DefaultPrecision; // 有効桁数
rmBack := BigDecimal.DefaultRoundingMode; // 除算丸めモード
Bigdecimal.DefaultPrecision := dpcs + 5;
BigDecimal.DefaultRoundingMode := rmNearesteven;
D180 := '180';
rad := deg * big_pi(dpcs + 5);
rad := rad.RoundToPrecision(dpcs + 5);
rad := rad / D180;
StopWatch := TStopwatch.StartNew;
// tan(x)
Bigdecimal.DefaultPrecision := dpcs;
ans := tan_big(rad);
StopWatch.Stop;
ElapsedMillseconds := StopWatch.ElapsedMilliseconds;
Form1.Edit1.text := '時間 = ' + intTostr(ElapsedMillseconds) + 'msec';
// 答え表示
// rad := rad.RoundToPrecision(dpcs div 2);
memo1.Lines.Append('角度deg =' + deg.ToPlainString);
// memo1.Lines.Append('角度RAD =' + rad.ToPlainString);
memo1.Lines.Append('tan(x) =' + ans.ToPlainString);
Bigdecimal.DefaultPrecision := back; // 有効桁数戻し
BigDecimal.DefaultRoundingMode := rmBack; // 除算丸めモード復帰
end;
procedure TForm1.ClearbtnClick(Sender: TObject);
begin
memo1.Clear;
end;
end.
tan_x.zip
三角関数、逆三角関数、その他関数 に戻る