流体　流線の差分法による計算作図
　差分法（Ｆｉｎｉｔｅ　Ｄｉｆｆｅｒｅｎｃｅ　Ｍｅｔｈｏｄ）

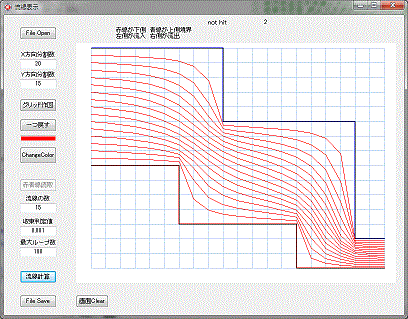
　此処では、理想流体の流線の計算を差分法で計算するプログラム例を取り上げています。
ポテンシャル流れ（渦なし流れ）の計算です。
流体計算の理論式は、専門書を参照して下さい。
まず最初に、流域作図用のグリッドを表示させます、Ｘ方向の分割数、Ｙ方向の分割数を決め、グリッド作図ボタンでグリッドを表示します。
グリッドは分割数を多くして、細かくしたほうがきれいな流線が得られます。
しかし、あくまでも理想流体の流線なので、参考程度にしかなりませんが、試してみるのも良いでしょう。
グリッドを表示したら、

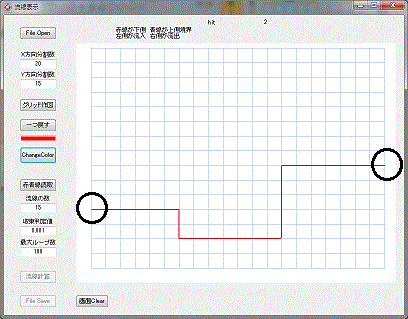
　赤線で、下側の領域を線引きします、線を引く場合、グリッドの一番左から、右へ向かって線を引きますが、斜めの線は使用出来ません。
又、戻ることもしてはいけません。
線の位置は、自動的にマウスカーソルの一番近いグリッドに自動的にヒットするようになってますが、ゆっくりと操作しないと、認識出来ない場合があります。
次に、上側の領域を青で作図します。

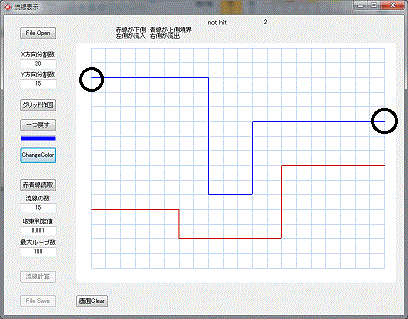
　上側の領域も、グリッドの一番左から、右側まで、線を引きます。
計算上流域の幅は、最低でもグリッド二つ分は必要です。

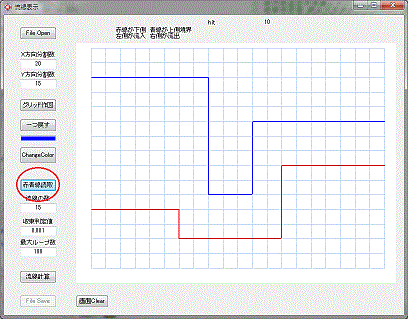
上下の線を引き終わったら、赤青線読取ボタンで、領域の認識を行います。

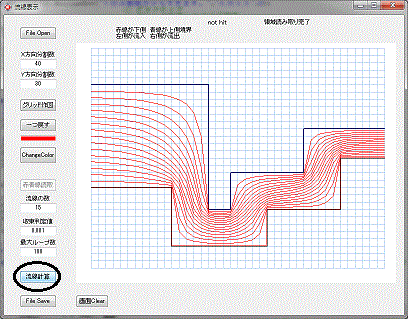　次に流線計算ボタンをクリックすれば、流線が作図されます。
例なので、領域を作図したものと、流線を作図した図が違っています。
流線の入り口は左側で、出口は右側と定義していますが、理想流体という事で、どちらを入り口とするかは、作図する人のとり方しだいです。

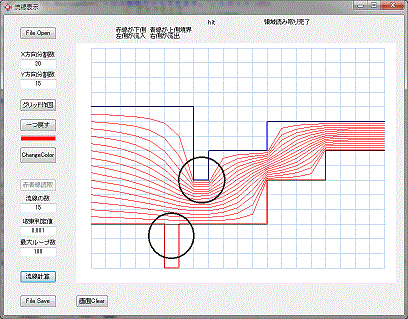
　水平方向の流域の溝形状の幅は、グリッド二個以上必要です、左図下側の線のようにグリッド一個だと、その部分は計算できないので、無視されてその部分は無い事になります。
流域の中に凸形状になっている場合は、凸の幅がグリッド一個分でも問題ありません。

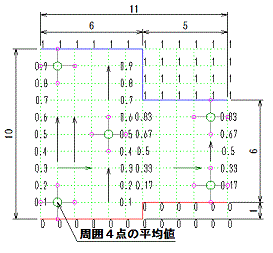
　左図は、差分法の計算手順を図で表したものです。
横方向は１１分割　縦方向は１０分割となっていますのでデーターの配列の大きさは、それぞれ１プラスされ１２×１１の配列となります。
流入側は、幅１０流出側は幅６です。
下側の流界までは、０を書き込み、上側の流界以上は１を書き込みます。
流域内は、縦方向の間隔で０～1の値を等間隔で設定します。
計算の開始点は、配列を(０,　 ０) ～ （１１，１０）　とすると計算は左図の例では、（１，　１）から計算をはじめ、最初は（１，　９）まで計算し、次の列に移ります。
５回列を移動すると、そこは流域の幅が狭くなりますので、左図例では（６，　２）から（６，　６）迄計算し次の列に移動します。最後は（１０，６）で、一回のループが終了します。
計算は、計算点周囲の四点の平均値を計算し、計算点のところに書き込みます。
計算の収束は計算前の値と、計算時の値の差が、全ての計算点で、収束判定値以下になった時を計算終了とします。
収束判定値以下になるまで、計算のループを繰り返します。
収束しない場合は、ループ回数の上限を設定し、上限に達したところで計算を打ち切ります。

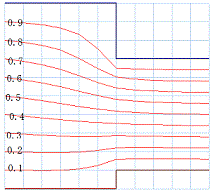
　流線の作図を流入側から行うとした場合で、流線の数を９本とすると、流線のとる値は　０．１，　０．２，　０．３　～　０．９　の値をとる事になります。
図の左流入側から、右流出側まで、その値をとる点を結べば、流線図となります。
計算は、グリッドの位置でしか計算されないので、グリッドの中間は補間法により計算します。
　此処では、差分の計算に　０～１　で計算していますが、０～３でも、－２～２　でも問題ありません。
差分法では、流入、流出が平行である必要があるのと、流れの方向が逆になるような流線はとる事が出来ません。
流れの方向を自由に計算する場合は、有限要素法を使用する事になります。