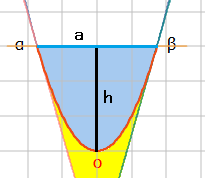
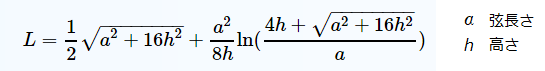
放物線の弧の長さは、上記式で計算しますが、α と β の高さが同じ場合の計算なので、高さが違う場合は、それぞれの高さと弦長さで計算し、加算後二分の一にします。
計算の詳細や証明は、インターネットで放物線を検索してください。
放物線と直線の交点
放物線
y = ax2 + bx + c
と直線 y = ax + b
の交点と 交点を通る放物線との接線の交点で出来る扇型部と弓型部の面積計算。
双曲線と直線の交点の計算に似ていますが、交点と原点を結ぶ直線と、接線の部分が異なっています。
交点を求める計算はの、連立方程式は二次方程式になるので、簡単に求めることが出来ます。
接線は、交点を α[x,y] とすると
傾き m = 2aαx + b
で求め、Y軸との交点 は d = -mαx + αy
となり y = mx + d の直線 となります。
接線同士の交点Xの値は、放物線上の交点Xの値の平均値となります。
放物線と、直線で囲まれた弓型部面積は、放物線と直線の交点のXの値を α、β
とすると
s = |a(β-α)3|/6 六分の一公式
扇型部の面積は、α、β、二接線の交点の三点から三角形の面積を計算し、弓型部の面積を差し引きます。
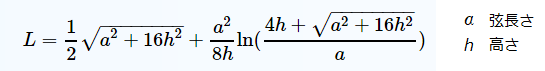
放物線の弧の長さは、上記式で計算しますが、α と β
の高さが同じ場合の計算なので、高さが違う場合は、それぞれの高さと弦長さで計算し、加算後二分の一にします。
計算の詳細や証明は、インターネットで放物線を検索してください。
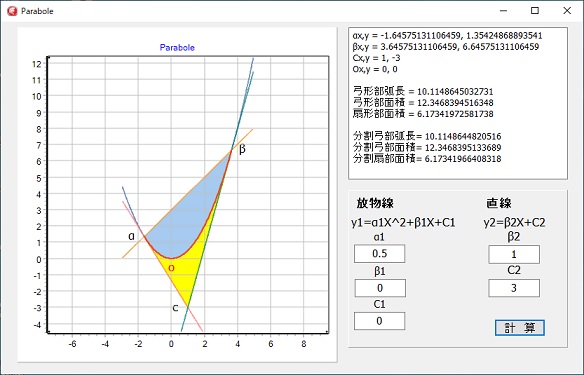左図は、放物線と直線の交点を計算するプログラムの実行画面です。
面積、弧長の計算が正しいかどうかは、双曲線の弧長、面積計算と同じように、分割積分の計算で確認しています。
放物線の原点(頂点)Ｏ、直線との交点 α、β、交点を通る接線同志の交点Ｃ、扇片部の面積（黄色）、弓形部の面積（青色）の計算をします。
プログラム
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, VclTee.TeeGDIPlus, Vcl.StdCtrls, Vcl.ExtCtrls,
VCLTee.TeEngine, VCLTee.Series, VCLTee.TeeProcs, VCLTee.Chart;
type
TForm1 = class(TForm)
Chart1: TChart;
Series1: TLineSeries;
Series2: TLineSeries;
Memo1: TMemo;
Series3: TLineSeries;
Series4: TLineSeries;
Image1: TImage;
Panel1: TPanel;
Label3: TLabel;
Label1: TLabel;
Label4: TLabel;
Label2: TLabel;
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
LabeledEdit3: TLabeledEdit;
LabeledEdit4: TLabeledEdit;
LabeledEdit5: TLabeledEdit;
Button1: TButton;
Series5: TPointSeries;
Series6: TLineSeries;
procedure Button1Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
private
{ Private 宣言 }
function datainput: boolean;
function calc_point_of_intersection: boolean;
procedure graphDraw;
function calc_arc: boolean;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
var
x1, y1 : double; // 直線と放物線の交点 左
x2, y2 : double; // 直線と放物線の交点 右
alpha, alpy : double; // 放物線原点より遠いほうの交点
beta, bety : double; // 放物線原点より近いほうの交点
xc0, yc0 : double; // 放物線の原点
xcc, ycc : double; // 接線同士の交点
a1, b1, c1 : double; // 放物線 y = a1X^2 + b1X + c1
b2, c2 : double; // 直線 y = b2X + c2
CF : boolean; // 交点の有無フラグ
Lb3, Lc3, Lb4, Lc4 : double; // 接線の値 y = LbX + Lc
// 入力値処理
function TForm1.datainput: boolean;
var
ch: integer;
begin
result := false;
val(LabeledEdit1.Text, a1, ch);
if ch <> 0 then begin
application.MessageBox('α1の値に間違いがあります。','',0);
exit;
end;
if a1 = 0 then begin
application.MessageBox('α1の値はゼロではいけません。','',0);
exit;
end;
val(LabeledEdit2.Text, b1, ch);
if ch <> 0 then begin
application.MessageBox('β1の値に間違いがあります。','',0);
exit;
end;
val(LabeledEdit3.Text, c1, ch);
if ch <> 0 then begin
application.MessageBox('C1の値に間違いがあります。','',0);
exit;
end;
val(LabeledEdit4.Text, b2, ch);
if ch <> 0 then begin
application.MessageBox('β2の値に間違いがあります。','',0);
exit;
end;
val(LabeledEdit5.Text, c2, ch);
if ch <> 0 then begin
application.MessageBox('C2の値に間違いがあります。','',0);
exit;
end;
result := true;
end;
// 弓形部長さ計算
// 右と左に分けて計算
function TForm1.calc_arc: boolean;
var
L, L1, L2 : double;
s1, s2 : double;
a3, b3 : double;
a4, b4 : double;
begin
xc0 := -b1 / a1 / 2; // 放物線 変曲点X 中心位置
yc0 := xc0 * xc0 * a1 + xc0 * b1 + c1; // 変曲点y 中心位置
memo1.Lines.Add('Ox,y = ' + floatTostr(xc0) + ', ' + floatTostr(yc0));
b3 := abs(x1 - xc0) * 2;
a3 := abs(y1 - yc0); // 放物線のx1の高さ
if a3 <> 0 then begin
s1 := sqrt(b3 * b3 + 16 * a3 * a3);
L1 := s1 / 2 + b3 * b3 / 8 / a3 * ln((4 * a3 + s1) / b3);
end
else L1 := 0;
b4 := abs(x2 - xc0) * 2;
a4 := abs(y2 - yc0); // 放物線のx2の高さ
if a4 <> 0 then begin
s2 := sqrt(b4 * b4 + 16 * a4 * a4);
L2 := s2 / 2 + b4 * b4 / 8 / a4 * ln((4 * a4 + s2) / b4);
end
else L2 := 0;
if (x1 - xc0) * (x2 - xc0) > 0 then L := abs(L2 - L1) / 2
else L := (L1 + L2) / 2;
memo1.Lines.Add('');
memo1.Lines.Add('弓形部弧長 = ' + floatTostr(L));
result := true;
end;
// 放物線弓形部の面積
// 1/6公式で計算
function TForm1.calc_point_of_intersection: boolean;
var
i , n: integer;
dx : double;
Xmax, Xmin : double;
x, y : double;
a0, b0, c0 : double;
d, e, s : double;
ycp : double;
y3, y4, ds, ss : double;
x3, x4 : double;
begin
result := False;
a0 := a1; // 放物線と直線の交点計算
b0 := b1 - b2;
c0 := c1 - c2;
d := b0 * b0 - 4 * a0 * c0;
if d < 0 then exit; // ルートの中がマイナスなら交点なし
e := sqrt(d);
x1 := (-b0 - e) / 2 / a0; // 交点x1座標
x2 := (-b0 + e) / 2 / a0; // 交点x2座標
alpha := x1;
beta := x2;
y1 := x1 * b2 + c2; // 交点y1座標
y2 := x2 * b2 + c2; // 交点y2座標
alpy := y1;
bety := y2;
if beta < alpha then begin // 値の大きさで入れ替え β > αにします、面積計算の為
beta := x1;
bety := y1;
alpha := x2;
alpy := y2;
end;
memo1.Clear;
memo1.Lines.Add('αx,y = ' + floatTostr(alpha) + ', ' + floatTostr(alpy));
memo1.Lines.Add('βx,y = ' + floatTostr(beta) + ', ' + floatTostr(bety));
Lb3 := 2 * a1 * alpha + b1; // y1=m1x+c1 のm1の値
Lc3 := - Lb3 * alpha + alpy; // y1=m1x+c1 のc1の値
Lb4 := 2 * a1 * beta + b1; // y2=m2x+c2 のm2の値
Lc4 := - Lb4 * beta + bety; // y2=m2x+c2 のc2の値
xcc := (Lc4 - Lc3) / (Lb3 - Lb4); // y1=m1x+c1 と y2=m2x+c2 の交点xの値
ycc := Lb3 * xcc + Lc3; // y1=m1x+c1 と y2=m2x+c2 の交点yの値
memo1.Lines.Add('Cx,y = ' + floatTostr(xcc) + ', ' + floatTostr(ycc));
if not calc_arc then exit;
result := true;
s := abs(a1) * (beta - alpha) * (beta - alpha) * (beta - alpha) / 6; // 弓形部面積計算 1/6公式
memo1.Lines.Add('弓形部面積 = ' + floatTostr(s));
// 三点の値 x1,y1, xcc,tcc x2,y2 の面積 - 弓形面積
x3 := x1 - xcc;
x4 := x2 - xcc;
y3 := y1 - ycc;
y4 := y2 - ycc;
ds := abs(x3 * y4 - x4 * y3) / 2; // 三角形面積
ss := ds - s; // 扇形部面積
memo1.Lines.Add('扇形部面積 = ' + floatTostr(ss));
if (Lb3 = Lb4) then exit;
if a1 > 0 then begin
if yc0 > ycc then ycp := ycc - (yc0 - ycc) / 2 // 直線のyの描画範囲
else ycp := yc0 - 0.1 / a1;
end
else begin
if yc0 < ycc then ycp := ycc + (ycc - yc0) / 2 // 放物線a1x^2のa1の符号±で方向変更
else ycp := yc0 - 0.1 / a1;
end;
n := 1000;
Xmin := x1 - (x2 - X1) / 4;
Xmax := x2 + (X2 - X1) / 4;
dx := (Xmax - Xmin) / n;
for i := 0 to n do begin // 接線1の描画
x := i * dx + Xmin;
y := Lb3 * x + Lc3;
if a1 > 0 then if y > ycp then Series3.AddXY(x,y);
if a1 < 0 then if y < ycp then Series3.AddXY(x,y);
end;
for i := 0 to n do begin // 接線2の描画
x := i * dx + Xmin;
y := Lb4 * x + Lc4;
if a1 > 0 then if y > ycp then Series4.AddXY(x,y);
if a1 < 0 then if y < ycp then Series4.AddXY(x,y);
end;
end;
// 面積 弧の長さΔx分割計算
// 放物線と直線の描画
procedure TForm1.graphDraw;
var
i, n : integer;
dx, dx2 : double;
Xmax, Xmin : double;
Ymin : double;
Hmax, Hmin : double;
Vmax, Vmin : double;
x0, y0 : double;
y3 : double;
L, ls : double;
x, y : double;
ypl, ypm : integer;
xpl, xpm : integer;
ax, ay : double;
ysp, ypp, xsp : integer;
fys : integer;
begin
if CF then begin // 交点があった場合の面積と弧の長さ分割計算
n := 10000;
dx := (x2 - x1) / n;
L := 0;
x0 := x1; // 最初のx,y
y0 := x0 * x0 * a1 + x0 * b1 + c1;
for i := 1 to n do begin
x := i * dx + x1; // 次の x, y
y := x * x * a1 + x * b1 + c1;
Xmin := (x - x0); // x差分計算
Ymin := (y - y0); // y差分計算
ls := sqrt(Xmin * Xmin + Ymin * Ymin); // 微小距離計算
L := L + Ls; // 合計値
x0 := x;
y0 := y;
end;
memo1.Lines.Add('');
memo1.Lines.Add('分割弓部弧長= ' + floatTostr(L));
dx := (x2 - x1) / n;
dx2 := dx / 2;
L := 0;
for i := 0 to n - 1 do begin
x := i * dx + dx2 + x1; // xの値
y3 := x * b2 + c2; // x位置の直線yの値
y := x * x * a1 + x * b1 + c1 - y3; // x位置の放物線yの値と直線yの値の差
ls := y * dx; // 微小間隔の面積
L := L + Ls; // 合計値
end;
L := abs(L);
memo1.Lines.Add('分割弓部面積= ' + floatTostr(L));
L := 0;
for i := 0 to n - 1 do begin
x := i * dx + dx2 + x1; // xの値
if x < xcc then
y3 := x * Lb3 + Lc3 // 接線1yの値
else
y3 := x * Lb4 + Lc4; // 接線2yの値
y := x * x * a1 + x * b1 + c1 - y3; // x位置の放物線yの値と直線yの値の差
ls := y * dx; // 微小間隔の面積
L := L + Ls; // 合計値
end;
L := abs(L);
memo1.Lines.Add('分割扇部面積= ' + floatTostr(L));
dx := (x2 - x1) / 100;
for i := 0 to 100 do begin // 弧部赤作図
x := i * dx + x1;
y := x * x * a1 + x * b1 + c1;
Series6.AddXY(x, y);
end;
end;
// 放物線と交わる直線の描画
n := 1000;
Xmin := x1 - (x2 - x1) / 4; // 描画範囲
Xmax := x2 + (x2 - x1) / 4;
dx := abs(Xmax - Xmin) / n;
if (Xmax - Xmin) = 0 then begin // 接線となるときの描画範囲
Xmin := x1 - abs(1 / a1);
Xmax := x1 + abs(1 / a1);
dx := (Xmax - Xmin) / n;
CF := False;
end;
if Xmax < Xmin then Xmin := Xmax;
for i := 0 to n do begin
x := i * dx + Xmin;
y := x * x * a1 + x * b1 + c1; // 放物線描画
Series1.AddXY(x, y);
y := x * b2 + c2; // 直線描画
Series2.AddXY(x, y);
end;
Chart1.Update;
application.ProcessMessages; // 描画待ち
// Chartの縦横比を同じに設定します
Hmax := Chart1.BottomAxis.Maximum;
Hmin := Chart1.BottomAxis.Minimum;
Vmax := Chart1.LeftAxis.Maximum;
Vmin := Chart1.LeftAxis.Minimum;
if (Hmax - Hmin) > (Vmax - Vmin) then begin
dx2 := ((Hmax - Hmin) - (Vmax - Vmin)) / 2;
Vmax := Vmax + dx2;
Vmin := Vmin - dx2;
end
else begin
dx2 := ((Vmax - Vmin) - (Hmax - Hmin)) / 2;
Hmax := Hmax + dx2;
Hmin := Hmin - dx2;
end;
Series5.AddXY(Hmin, Vmax); // Hmax,Hmin,Vmax,Vmin 反映の為の Series
Series5.AddXY(Hmin, Vmin);
Series5.AddXY(Hmax, Vmin);
Chart1.Update;
application.ProcessMessages; // 描画待ち
if not CF then exit; // 交点がなかったら塗りつぶしなし
ypl := chart1.LeftAxis.IStartPos; // y軸スタート座標
ypm := chart1.LeftAxis.IEndPos; // y軸エンド座標
xpl := chart1.BottomAxis.IStartPos; // x軸スタート座標
xpm := chart1.BottomAxis.IEndPos; // x軸エンド座標
Image1.Canvas.Pen.Color := clSkyblue;
Image1.Canvas.Pen.Style := psSolid;
Image1.Canvas.Pen.Width := 1;
ax := (xpm - xpl) / (Hmax - Hmin); // x方向座標変換係数
ay := (ypm - ypl) / (Vmax - Vmin); // y方向座標変換係数
xsp := round((x2 - Hmin) * ax) + xpl;
ysp := round((x1 - Hmin) * ax) + xpl;
n := abs(xsp - ysp); // 分割数
dx := (x2 - x1) / n;
for i := 1 to n - 1 do begin
x := i * dx + x1; // xの値
xsp := round((x - Hmin) * ax) + xpl;
y3 := x * b2 + c2; // 直線yの値
ysp := round((Vmax - y3) * ay) + ypl; // 直線yの座標
y := x * x * a1 + x * b1 + c1; // 放物線yの値
ypp := round((Vmax - y) * ay) + ypl; // 放物線yの座標
Image1.Canvas.MoveTo(xsp, ysp); // 直線のx位置から
Image1.Canvas.LineTo(xsp, ypp); // 放物線xの位置へ線描画
end;
Image1.Canvas.Pen.Color := clYellow;
for i := 1 to n - 1 do begin
x := i * dx + x1; // xの値
xsp := round((x - Hmin) * ax) + xpl;
if x < xcc then
y3 := x * Lb3 + Lc3 // 接線1yの値
else
y3 := x * Lb4 + Lc4; // 接線2yの値
ysp := round((Vmax - y3) * ay) + ypl; // 直線yの座標
y := x * x * a1 + x * b1 + c1; // 放物線yの値
ypp := round((Vmax - y) * ay) + ypl; // 放物線yの座標
Image1.Canvas.MoveTo(xsp, ysp); // 直線のx位置から
Image1.Canvas.LineTo(xsp, ypp); // 放物線xの位置へ線描画
end;
application.ProcessMessages; // 描画待ち
fys := 13;
Image1.Canvas.Font.Size := fys;
Image1.Canvas.Font.Color := cLBlack;
xsp := round((beta - Hmin) * ax) + xpl + 10;
ysp := round((Vmax - bety) * ay) + ypl - fys;
Image1.Canvas.TextOut(xsp,ysp,'β'); // 交点yの座標β
xsp := round((alpha - Hmin) * ax) + xpl - 22;
ysp := round((Vmax - alpy) * ay) + ypl - fys;
Image1.Canvas.TextOut(xsp,ysp,'α'); // 交点yの座標α
xsp := round((xcc - Hmin) * ax) + xpl - 22;
ysp := round((Vmax - ycc) * ay) + ypl - fys;
Image1.Canvas.TextOut(xsp,ysp,'c'); // 二接線の交点座標α
xsp := round((xc0 - Hmin) * ax) + xpl - 4;
if a1 > 0 then fys := 0;
ysp := round((Vmax - yc0) * ay) + ypl - fys * 2;
if (xsp + fys < xpm) and (xsp > xpl)
and (ysp + fys < ypm) and (ysp > ypl) then begin
Image1.Canvas.Font.Color := cLRed;
Image1.Canvas.TextOut(xsp,ysp,'o'); // 放物線の座標α
end;
chart1.BackImage.Bitmap := Image1.Picture.Bitmap;
end;
procedure TForm1.Button1Click(Sender: TObject);
begin
Series1.Clear;
Series2.Clear;
Series3.Clear;
Series4.Clear;
Series5.Clear;
Series6.Clear;
Image1.Canvas.Brush.Color := clWhite;
Image1.Canvas.Brush.Style := bsSolid;
Image1.Canvas.FillRect(rect(0, 0, Image1.Width, Image1.Height));
Image1.Canvas.Brush.Style := bsClear;
chart1.BackImage.Bitmap := Image1.Picture.Bitmap;
if not datainput then exit;;
CF := True;
if not calc_point_of_intersection then begin
Memo1.Clear;
Memo1.Lines.Add('交点無し');
CF := False;
x1 := b1 / 2 - abs(1 / a1); // 交点なし時の作図範囲設定
x2 := b1 / 2 + abs(1 / a1);
end;
graphDraw;
end;
procedure TForm1.FormCreate(Sender: TObject);
var
FB : TBitmap;
begin
Image1.Visible := false;
FB := TBitmap.Create;
FB.Height := Chart1.Height;
FB.Width := Chart1.Width;
Image1.Height := Chart1.Height;
Image1.Width := Chart1.Width;
Image1.Picture.Bitmap := FB;
FB.Free;
end;
end.
parabole.zip