 左図は関数
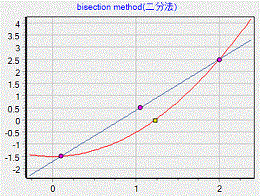
f(x)=x2-1.5 のグラフと範囲[a,b]、f(x)=0 のxの値を示したグラフです。
左図は関数
f(x)=x2-1.5 のグラフと範囲[a,b]、f(x)=0 のxの値を示したグラフです。xの値は簡単に計算で求める事が出来ますが、これは非線形方程式の例なので無視をしてください。
この方程式の場合、ゼロ点が二か所有ります、範囲[a,b]の指定で、どちらのゼロ点を求めるかが決まります。
曲線の最下点、最上点がゼロと場合の検出は出来ません。
方程式のグラフを作成してから、範囲指定をすると良いでしょう。
非線形方程式の数値解法
非線形方程式の場合、関数f(x)=0を満足するxの値を容易に見つける事が出来ない場合があります。
そこで、プログラムにより、根の近似値を見つけ出そうとするものです。
1.二分法
関数f(x)が連続関数で、根が区間[a,b]の間なあり、f(a)f(b)<0となる場合、 aとbの二分の一の値c=(a+b)/2
f(c)の値を計算、f(c)の値が負数なら例えばaの値をa=cとし、正数ならb=cとして計算を繰り返して、決められた値以下になるまで計算を繰り返し近似値を求めるものです。
条件が揃っていれば、必ず近似値を求めねことが出来ます。
 左図は関数
f(x)=x2-1.5 のグラフと範囲[a,b]、f(x)=0 のxの値を示したグラフです。
左図は関数
f(x)=x2-1.5 のグラフと範囲[a,b]、f(x)=0 のxの値を示したグラフです。
xの値は簡単に計算で求める事が出来ますが、これは非線形方程式の例なので無視をしてください。
この方程式の場合、ゼロ点が二か所有ります、範囲[a,b]の指定で、どちらのゼロ点を求めるかが決まります。
曲線の最下点、最上点がゼロと場合の検出は出来ません。
方程式のグラフを作成してから、範囲指定をすると良いでしょう。
プログラム
// bisection method(二分法) 非線形方程式の数値解析 // 閉区間[a,b]で連続な関数f(x)でf(a)*f(b)<0であるならば、f(α)=0となるαの値は // 閉区間[a,b]内に存在する。 // 最初にf(a)*f(b)<0となる中間点を見つけて、中点c=(a+b)/2を新しい端点として計算をくりかえし // 前のcの値coと新たに計算したcnの値の差が決められた値以下になったらαの近似値とします。 // 接点の検出は難しい unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, VclTee.TeeGDIPlus, VCLTee.Series, Vcl.StdCtrls, Vcl.Buttons, Vcl.ExtCtrls, VCLTee.TeEngine, VCLTee.TeeProcs, VCLTee.Chart; type TForm1 = class(TForm) Chart1: TChart; Series1: TLineSeries; Series2: TLineSeries; LabeledEdit1: TLabeledEdit; LabeledEdit2: TLabeledEdit; BitBtn1: TBitBtn; Memo1: TMemo; Series3: TPointSeries; Series4: TPointSeries; procedure BitBtn1Click(Sender: TObject); private { Private 宣言 } procedure chart_graph(a, b: double); public { Public 宣言 } end; var Form1: TForm1; implementation {$R *.dfm} // 関数f(x)の計算式 非線形方程式 // 接点の検出は難しい function f(x: double): double; begin result := x * x - 1.5; end; // 区間[a,b]の関数f(x)のグラフを作図 procedure TForm1.chart_graph(a, b: double); const n = 100; var x, xs, xe, dx: double; ys, ye, dy : double; y : double; i : integer; begin series1.clear; series2.clear; series3.clear; series4.clear; if a = b then exit; // 範囲がゼロだったら終了 xs := a - (b - a) / 5; xe := b + (b - a) / 5; dx := (xe - xs) / n; for i := 0 to n do begin x := xs + i * dx; y := f(x); series1.AddXY(x, y); end; ys := f(a); ye := f(b); series3.AddXY(a, ys); series3.AddXY(b, ye); dy := (ye - ys) / (b - a); dx := (b - a) / n; for i := -20 to n + 20 do begin x := i * dx; y := (dy * x) + ys; series2.AddXY(x + a, y); end; x := (a + b) / 2; y := (dy * (x - a)) + ys; series3.AddXY(x, y); end; // 二分法によるf(α)=0となるαの近似値計算 function bisection_method(a, b, epsilon: double; var loop: integer): double; var c, fc, fa, fac : double; begin c := abs(a) + abs(b); while abs(a - b) > epsilon * 10 do begin c := (a + b) / 2; // aとb の中間値 fc := f(c); if fc = 0 then break; fa := f(a); fac := fa * fc; if fac < 0 then b := c; if fac > 0 then a := c; inc(loop); end; result := c; // c = αの近似値 end; // 計算実行 procedure TForm1.BitBtn1Click(Sender: TObject); var a, b, alpha, y : double; ch, loop : integer; epsilon, tmp : double; begin memo1.Clear; val(labelededit1.Text, a, ch); if ch <> 0 then begin application.MessageBox('初期にaに間違いが有ります。','注意',0); exit; end; val(labelededit2.Text, b, ch); if ch <> 0 then begin application.MessageBox('初期にbに間違いが有ります。','注意',0); exit; end; if a - b = 0 then begin application.MessageBox('範囲[a,b]がゼロです。','注意',0); exit; end; // グラフ作成 chart_graph(a, b); if f(a) * f(b) >= 0 then begin application.MessageBox('f(a)×f(b)の値がプラスになりますマイナスになるようにして下さい 。','注意',0); exit; end; // 収束判定値計算 epsilon := 1; repeat epsilon := epsilon / 2; tmp := 1 + epsilon; until tmp = 1; epsilon := epsilon * 2; // 非線形方程式の計算 loop := 0; alpha := bisection_method(a, b, epsilon, loop); // 検算 y := f(alpha); // 計算結果表示 if abs(y) > epsilon * 1000 then begin memo1.Lines.Append('ループ数 ' + intTostr(loop)); memo1.lines.Append('範囲[a,b]の値がf(x)=0 の範囲外です。'); memo1.lines.Append('又はf(x)=0の値が接点です。'); exit; end; series4.AddXY(alpha, y); memo1.Lines.Append('f(x) = x^2 - 1.5'); memo1.Lines.Append('ループ数 ' + intTostr(loop)); memo1.Lines.Append('収束判定値'); memo1.Lines.Append(floatTostr(epsilon)); memo1.Lines.Append('f(α)=0'); memo1.Lines.Append('α= ' +floatTostr(alpha)); memo1.Lines.Append('検算 y = f(α)'); memo1.Lines.Append('y= ' +floatTostr(y)); end; end.
2 挟み撃ち法
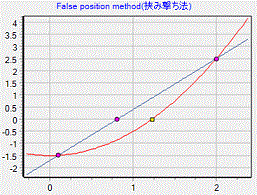
挟み撃ち法は、二分法の改良で、二点a,bを結ぶ直線が、x軸と交わる点を新しい端点として計算する方法です。
二分法に対して、約二分の一の計算数で収束します。
範囲[a,b]の条件は、二分法と同じです。
プログラム
// False position method(挟み撃ち法) 非線形方程式の数値解析 // 閉区間[a,b]で連続な関数f(x)でf(a)*f(b)<0であるならば、f(α)=0となるαの値は // 閉区間[a,b]内に存在する。 // 最初にf(a)*f(b)<0となる中間点を見つけて、中間点を二点を結ぶ直線がx軸と交わる点を // 新しい端点として計算をくりかえし // 前のcの値coと新たに計算したcnの値の差が決められた値以下になったらαの近似値とします。 unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, VclTee.TeeGDIPlus, VCLTee.Series, Vcl.StdCtrls, Vcl.Buttons, Vcl.ExtCtrls, VCLTee.TeEngine, VCLTee.TeeProcs, VCLTee.Chart; type TForm1 = class(TForm) Chart1: TChart; Series1: TLineSeries; Series2: TLineSeries; LabeledEdit1: TLabeledEdit; LabeledEdit2: TLabeledEdit; BitBtn1: TBitBtn; Memo1: TMemo; Series3: TPointSeries; Series4: TPointSeries; procedure BitBtn1Click(Sender: TObject); private { Private 宣言 } procedure chart_graph(a, b: double); public { Public 宣言 } end; var Form1: TForm1; implementation {$R *.dfm} // 関数f(x)の計算式 非線形方程式 // 接点の検出は難しい function f(x: double): double; begin result := x * x - 1.5; end; // 区間[a,b]の関数f(x)のグラフを作図 procedure TForm1.chart_graph(a, b: double); const n = 100; var x, xs, xe, dx: double; ys, ye, dy : double; y : double; i : integer; begin series1.clear; series2.clear; series3.clear; series4.clear; if a = b then exit; // 範囲がゼロだったら終了 xs := a - (b - a) / 5; xe := b + (b - a) / 5; dx := (xe - xs) / n; for i := 0 to n do begin x := xs + i * dx; y := f(x); series1.AddXY(x, y); end; ys := f(a); ye := f(b); series3.AddXY(a, ys); series3.AddXY(b, ye); dy := (ye - ys) / (b - a); dx := (b - a) / n; for i := -20 to n + 20 do begin x := i * dx; y := (dy * x) + ys; series2.AddXY(x + a, y); end; if abs(dy) > 0 then begin x := a - ys / dy; y := (dy * (x - a)) + ys; series3.AddXY(x, y); end; end; // 挟み撃ち法によるf(α)=0となるαの近似値計算 function False_position(a, b, epsilon: double; var loop: integer): double; var c, fc, fa, fb, fac : double; begin repeat fa := f(a); fb := f(b); c := (a * fb - b * fa) / (fb - fa); // x軸との交点 fc := f(c); if fc = 0 then break; fa := f(a); fac := fa * fc; if fac < 0 then b := c; if fac > 0 then a := c; inc(loop); until abs(fc) <= epsilon * 10; result := c; // c = αの近似値 end; // 計算実行 procedure TForm1.BitBtn1Click(Sender: TObject); var a, b, alpha, y : double; ch, loop : integer; epsilon, tmp : double; begin val(labelededit1.Text, a, ch); if ch <> 0 then begin application.MessageBox('初期にaに間違いが有ります。','注意',0); exit; end; val(labelededit2.Text, b, ch); if ch <> 0 then begin application.MessageBox('初期にbに間違いが有ります。','注意',0); exit; end; if a - b = 0 then begin application.MessageBox('範囲[a,b]がゼロです。','注意',0); exit; end; chart_graph(a, b); if f(a) * f(b) >= 0 then begin application.MessageBox('f(a)×f(b)の値がプラスになりますマイナスになるようにして下さい 。','注意',0); exit; end; // 収束判定値計算 epsilon := 1; repeat epsilon := epsilon / 2; tmp := 1 + epsilon; until tmp = 1; epsilon := epsilon * 2; // グラフ作成 chart_graph(a, b); // 非線形方程式の計算 loop := 0; alpha := False_position(a, b, epsilon, loop); // 検算 y := f(alpha); // 計算結果表示 memo1.Clear; if abs(y) > epsilon * 1000 then begin memo1.Lines.Append('ループ数 ' + intTostr(loop)); memo1.lines.Append('範囲[a,b]の値がf(x)=0 の範囲外です。'); memo1.lines.Append('又はf(x)=0の値が接点です。'); exit; end; series4.AddXY(alpha, y); memo1.Lines.Append('f(x) = x^2 - 1.5'); memo1.Lines.Append('ループ数 ' + intTostr(loop)); memo1.Lines.Append('収束判定値'); memo1.Lines.Append(floatTostr(epsilon)); memo1.Lines.Append('f(α)=0'); memo1.Lines.Append('α= ' +floatTostr(alpha)); memo1.Lines.Append('検算 y = f(α)'); memo1.Lines.Append('y= ' +floatTostr(y)); end; end.
3 ニュートン法
初期値xを設定します。
初期値xを通るf(x)との接線とx軸の交点x'を求め新しい点xとし、新しいx点を通るf(x)接線とx軸の交点を求める事を繰り返しf(x)=0となるxの近似値を求めます。
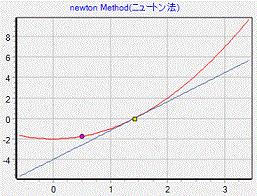
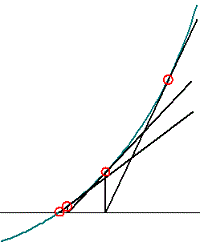
非常に収束が速く、通常10ループ以下で収束します。
方程式f(x)に対する微分式f'(x)が必要となります。
ニュートン法による計算として、逆インボリュート計算が有ります。
インボリュートは歯車の噛み合い曲線として用いられるもので、歯面の圧力角をθとすると、
tan(θ) - θ = inv θの単位はradです。
逆インボリュートは inv から 圧力角を求めます。
tan(θ) - θ - inv = 0 として非線形方程式
f(θ) を解くわけですが、微分式f'(θ)が必用となりますが、幸いなことに簡単に微分が出来ます。
f(θ) = tan(θ) - θ -
inv
tan'(θ) = sec2(θ)
sec(θ) = √{1+tan2(θ)}
から
f'(θ) = sec2(θ)
- 1 = tan2(θ)
微分 f'(θ) = tan2(θ)
プログラム
// newton Method(ニュートン法) 非線形方程式の数値解析 unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, VclTee.TeeGDIPlus, VCLTee.Series, Vcl.StdCtrls, Vcl.Buttons, Vcl.ExtCtrls, VCLTee.TeEngine, VCLTee.TeeProcs, VCLTee.Chart; type TForm1 = class(TForm) Chart1: TChart; Series1: TLineSeries; Series2: TLineSeries; Series3: TPointSeries; Series4: TPointSeries; LabeledEdit1: TLabeledEdit; LabeledEdit2: TLabeledEdit; BitBtn1: TBitBtn; Memo1: TMemo; procedure BitBtn1Click(Sender: TObject); private { Private 宣言 } procedure chart_graph(a, h: double); public { Public 宣言 } end; var Form1: TForm1; implementation {$R *.dfm} // 関数f(x)の計算式 非線形方程式 function f(x: double): double; begin result := x * x - 2; end; // f'(x) 微分値 function df(x: double): double; begin result := 2 * x; end; // 区間[a±h]の関数f(x)、df(x)のグラフを作図 procedure TForm1.chart_graph(a, h: double); const n = 100; var x, xs, xe, dx: double; y, dy : double; i : integer; begin series1.clear; series2.clear; series3.clear; series4.clear; xs := (a - h); xe := (a + h); dx := (xe - xs) / n; dy := df(a); for i := 0 to n do begin x := xs + i * dx; y := f(x); series1.AddXY(x, y); y := dy * (x - a); series2.AddXY(x, y); end; end; // ニュートン法によるf(α)=0となるαの近似値計算 function newton_Method(a, epsilon: double; var loop: integer): double; var ah : double; begin while loop < 1000 do begin inc(loop); ah := a - f(a) / df(a); if abs(ah - a) <= epsilon * abs(a) then break; a := ah; end; result := a; end; // 計算実行 procedure TForm1.BitBtn1Click(Sender: TObject); var a, h, alpha, y : double; ch, loop : integer; epsilon, tmp : double; begin val(labelededit1.Text, a, ch); if ch <> 0 then begin application.MessageBox('初期にaに間違いが有ります。','注意',0); exit; end; val(labelededit2.Text, h, ch); if ch <> 0 then begin application.MessageBox('グラフ範囲hに間違いが有ります。','注意',0); exit; end; if h <= 0 then begin application.MessageBox('グラフ範囲hがゼロです。','注意',0); exit; end; // 収束判定値計算 epsilon := 1; repeat epsilon := epsilon / 2; tmp := 1 + epsilon; until tmp = 1; epsilon := epsilon * 2; memo1.Clear; // 初期値の確認 if abs(df(a)) < epsilon then begin memo1.lines.Append('微分値df(a)の値がゼロに成ります'); memo1.lines.Append('初期値を変更して下さい。'); exit; end; // 非線形方程式の計算 loop := 0; alpha := newton_Method(a, epsilon, loop); if loop >= 1000 then begin memo1.lines.Append('収束しませんでした。'); memo1.lines.Append('初期値又は、方程式を見直して下さい。'); exit; end; // 検算 y := f(alpha); // 計算結果表示 memo1.Lines.Append('f(x) = x^2 - 2'); memo1.Lines.Append('ループ数 ' + intTostr(loop)); memo1.Lines.Append('収束判定値'); memo1.Lines.Append(floatTostr(epsilon)); memo1.Lines.Append('f(α)=0'); memo1.Lines.Append('α= ' +floatTostr(alpha)); memo1.Lines.Append('検算 y = f(α)'); memo1.Lines.Append('y= ' + floatTostr(y)); // グラフ作成 chart_graph(alpha, h); // f(x)グラフ series4.AddXY(alpha, y); // 解答値 series3.AddXY(a, f(a)); // 初期値 end; end.
4 ブレント法
ブレント法は、条件において二分法、挟み撃ち法(割線法)、逆二次補間を利用して、高速に収束させるものです。
ニュートン法は、高速に収束しますが、微分が出来ないと使用できないので、その場合は、ブレント法を使用します。
アルゴリズムについては、webで"ブレント法"で検索してください。
プログラム
// brent method(ブレント法) 非線形方程式の数値解析 unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, VclTee.TeeGDIPlus, VCLTee.Series, Vcl.StdCtrls, Vcl.Buttons, Vcl.ExtCtrls, VCLTee.TeEngine, VCLTee.TeeProcs, VCLTee.Chart; type TForm1 = class(TForm) Chart1: TChart; Series1: TLineSeries; Series2: TLineSeries; LabeledEdit1: TLabeledEdit; LabeledEdit2: TLabeledEdit; BitBtn1: TBitBtn; Memo1: TMemo; Series3: TPointSeries; Series4: TPointSeries; LabeledEdit3: TLabeledEdit; procedure BitBtn1Click(Sender: TObject); private { Private 宣言 } procedure chart_graph(a, b: double); public { Public 宣言 } end; var Form1: TForm1; implementation {$R *.dfm} // 関数f(x)の計算式 非線形方程式 function f(x: double): double; begin result := (x + 3) * (x - 1) * (x - 1); end; // 区間[a,b]の関数f(x)のグラフを作図 procedure TForm1.chart_graph(a, b: double); const n = 100; var x, xs, xe, dx: double; ys, ye, dy : double; y : double; i : integer; begin series1.clear; series2.clear; series3.clear; series4.clear; if a = b then exit; // 範囲がゼロだったら終了 xs := a - (b - a) / 5; xe := b + (b - a) / 5; dx := (xe - xs) / n; for i := 0 to n do begin x := xs + i * dx; y := f(x); series1.AddXY(x, y); end; ys := f(a); ye := f(b); series3.AddXY(a, ys); series3.AddXY(b, ye); dy := (ye - ys) / (b - a); dx := (b - a) / n; for i := -20 to n + 20 do begin x := i * dx; y := (dy * x) + ys; series2.AddXY(x + a, y); end; end; // ブレント法によるf(α)=0となるαの近似値計算 function brent_method(a, b, delta, epsilon: double; var loop: integer): double; var e, d, c, beta, alpha, p, q, r, s : double; begin c := a; d := b - a; e := d; while abs(f(b)) > epsilon do begin alpha := (a - b) / 2; beta := f(b) / f(c); if (abs(e) < delta) or (abs(f(c)) < abs(f(b))) then begin // 二分法 e := alpha; d := e; end else begin if a = c then begin // 線形補間 p := 2 * alpha * beta; q := 1 - beta; end else begin // 逆二次補間 q := f(c) / f(a); r := f(b) / f(a); p := beta * (2 * alpha * q * (q - r) - (b - c) * (r - 1)); q := (q - 1) * (r - 1) * (beta - 1); end; beta := e; e := d; if (abs(2 * p) < abs(3 * alpha * q)) and (abs(p) < abs(beta * q / 2)) then d := - p / q else begin // 二分法 e := alpha; d := e; end; end; if abs(d) > delta then s := b + d else if alpha > 0 then s := b + delta else s := b - delta; c := b; b := s; if f(b) * f(a) > 0 then begin a := c; e := b - c; d := e; end; if abs(f(a)) < abs(f(b)) then begin a := b; b := c; c := b; end; inc(loop); end; result := b; end; // 計算実行 procedure TForm1.BitBtn1Click(Sender: TObject); var a, b, alpha, y : double; ch, loop : integer; delta, tmp, epsilon : double; begin memo1.Clear; val(labelededit1.Text, a, ch); if ch <> 0 then begin application.MessageBox('初期にaに間違いが有ります。','注意',0); exit; end; val(labelededit2.Text, b, ch); if ch <> 0 then begin application.MessageBox('初期にbに間違いが有ります。','注意',0); exit; end; val(labelededit3.Text, epsilon, ch); if ch <> 0 then begin application.MessageBox('収束判定値に間違いが有ります。','注意',0); exit; end; // グラフ作成 chart_graph(a, b); if a - b = 0 then begin application.MessageBox('範囲[a,b]がゼロです。','注意',0); exit; end; if abs(f(b)) >= abs(f(a)) then begin application.MessageBox('|f(a)| <= |f(b)|です、変更して下さい。','注意',0); exit; end; if f(a) * f(b) >= 0 then begin application.MessageBox('f(a) * f(b) > 0、です変更して下さい。','注意',0); exit; end; // 収束判定値計算 delta := 1; repeat delta := delta / 2; tmp := 1 + delta; until tmp = 1; delta := delta * 2; if epsilon < delta * 100 then begin application.MessageBox('収束判定値が小さすぎます。','注意',0); exit; end; // 非線形方程式の計算 loop := 0; alpha := brent_method(a, b, delta, epsilon, loop); // 検算 y := f(alpha); // 計算結果表示 if abs(y) > epsilon * 10 then begin memo1.Lines.Append('ループ数 ' + intTostr(loop)); memo1.lines.Append('範囲[a,b]の値がf(x)=0 の範囲外です。'); memo1.lines.Append('又はf(x)=0の値が接点です。'); exit; end; series4.AddXY(alpha, y); memo1.Lines.Append('f(x) = (x + 3) * (x - 1)^2'); memo1.Lines.Append('ループ数 ' + intTostr(loop)); memo1.Lines.Append('収束判定値'); memo1.Lines.Append(floatTostr(epsilon)); memo1.Lines.Append('f(α)=0'); memo1.Lines.Append('α= ' +floatTostr(alpha)); memo1.Lines.Append('検算 y = f(α)'); memo1.Lines.Append('y= ' +floatTostr(y)); end; end.
下記でダウンロード出来るプログラムには、四つのプログラムが含まれます。
![]() bisection_method.zip
bisection_method.zip
三角関数、逆三角関数、その他関数、 連立一次方程式の解法 に戻る