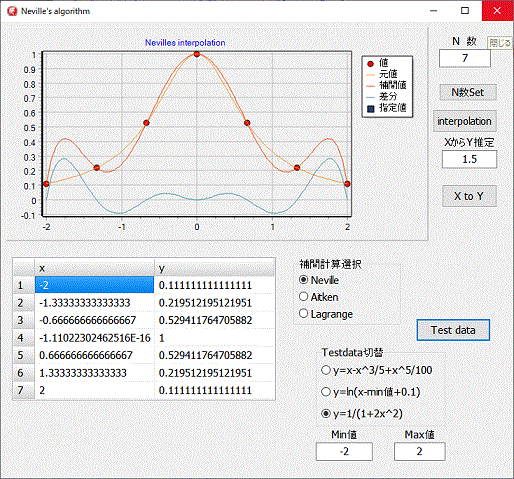
 プログラムは、ネヴィル、エイトケン、ラグランジェ補間を切り替えて計算確認出来るようになっています。
プログラムは、ネヴィル、エイトケン、ラグランジェ補間を切り替えて計算確認出来るようになっています。当然、計算結果は、全て同じです。
ネヴィル、エイトケン補間は、参考程度のものです。
詳細については、Webで検索して下さい。
ネヴィル補間
ネヴィルのアルゴリズムによる補間で、ラグランジュ補間の計算のアルゴリズムの一つです。
エイトケン補間
エイトケン補間は、ラグランジェ補間、ネヴィルのアルゴリズムと似たようなものです。
ネヴィル、エイトケンとも補間の結果は、多項式補間であり、ニュートン補間と同じ結果となります。
ニュートン、ラグランジェ、ネヴィル、エイトケンの補間は、計算手順が違うだけで、同じN-1の多項式の補間計算となります。
実用的には、n次多項式近似(polynomial approximation)を使用した方が良いでしょう。
多項式近似であれば、1~(N-1)次の次数を指定して、近似の計算が可能となります。
しかし、実際のばらつきのある測定データーを使用して、補間計算をするのには無理があります。
 プログラムは、ネヴィル、エイトケン、ラグランジェ補間を切り替えて計算確認出来るようになっています。
プログラムは、ネヴィル、エイトケン、ラグランジェ補間を切り替えて計算確認出来るようになっています。
当然、計算結果は、全て同じです。
プログラム
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, VclTee.TeeGDIPlus, Vcl.StdCtrls,
VCLTee.TeEngine, VCLTee.Series, Vcl.ExtCtrls, VCLTee.TeeProcs, VCLTee.Chart,
Vcl.Grids;
type
TForm1 = class(TForm)
Chart1: TChart;
StringGrid1: TStringGrid;
NEdit: TLabeledEdit;
NsetBtn: TButton;
interpolationBtn: TButton;
testdataBtn: TButton;
XEdit: TLabeledEdit;
Series1: TPointSeries;
Series2: TLineSeries;
Series3: TLineSeries;
Series4: TLineSeries;
Series5: TPointSeries;
Xin_interpolation: TButton;
RadioGroup2: TRadioGroup;
MinxEdit: TLabeledEdit;
MaxXEdit: TLabeledEdit;
RadioGroup1: TRadioGroup;
procedure testdataBtnClick(Sender: TObject);
procedure NsetBtnClick(Sender: TObject);
procedure interpolationBtnClick(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure Xin_interpolationClick(Sender: TObject);
private
{ Private 宣言 }
procedure GridSet(Sin, Colin: integer);
procedure FGridSet(Sin, Colin: integer); // グリッドサイズ変更
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses system.Math;
type
DArray = array of double;
var
x, y : Darray;
DEF : Boolean;
xmax, xmin, dx : double;
// グリッドサイズの変更
procedure TForm1.GridSet(Sin, Colin: integer); // グリッドサイズ変更
var // データー行の数は10迄
H, W :integer; // それ以上はスクロールする
begin
if (StringGrid1.ColCount = Colin) and (StringGrid1.RowCount = Sin) then exit;
StringGrid1.ColWidths[0] := 30;
StringGrid1.ColCount := Colin;
StringGrid1.RowCount := Sin;
if Sin <= 11 then // ストリンググリッドの大きさ設定
begin // 固定行を含め11行又はそれ以下の場合
H := (StringGrid1.DefaultRowHeight + 1) * Sin;
W := (StringGrid1.DefaultColWidth + 1) * (Colin - 1) + 31;
StringGrid1.ScrollBars := ssNone; // スクロールバーなし
end
else
begin // 固定行を含め11行より多い場合
H := (StringGrid1.DefaultRowHeight + 1) * (10 + 1);
W := (StringGrid1.DefaultColWidth + 1) * (Colin - 1) + 31;
StringGrid1.ScrollBars := ssVertical; // スクロールバー表示
end;
StringGrid1.ClientWidth := W;
StringGrid1.ClientHeight := H;
end;
// グリッド固定行の設定
procedure TForm1.FGridSet(Sin, Colin: integer);
var
E : integer;
begin
GridSet(Sin, Colin);
for E := 1 to Sin - 1 do
StringGrid1.Rows[E].Text := intTostr(E);
StringGrid1.Cols[1].Text := 'x';
StringGrid1.Cols[2].Text := 'y';
end;
// N数入力 エラー時 N < 0
function Ninput: integer;
var
N, ch : integer;
begin
result := -1;
val(Form1.Nedit.Text, N, ch);
if ch <> 0 then begin
application.MessageBox('N数の入力に間違いが有ります。','注意',0);
exit;
end;
if N > 100 then begin
application.MessageBox('N数は100迄にして下さい。','注意',0);
exit;
end;
if N < 3 then begin
application.MessageBox('N数は3以上にして下さい。','注意',0);
exit;
end;
result := N;
end;
// グリッドN数セット
procedure TForm1.NsetBtnClick(Sender: TObject);
var
N : integer;
begin
N := Ninput;
if N < 0 then exit;
GridSet(N + 1, 3);
end;
// xの値チェック 同じxの値があるか確認 同じ値無 true 有り false
function datacheck(x :DArray; N: integer): boolean;
var
i, j : integer;
begin
result := true;
for i := 0 to N - 1 do
for j := 0 to N - 1 do begin
if i <> j then
if x[i] - x[j] = 0 then begin
application.MessageBox(pchar('x' + inttostr(i+1) + '-x' + inttostr(j+1)
+ 'がゼロになります。'),'注意',0);
result := false;
exit;
end;
end;
for i := 0 to N - 2 do
if x[i] > x[i + 1] then begin
application.MessageBox(pchar('x' + inttostr(i+1) + '>x' + inttostr(i+2)
+ #13#10 +'値の大きさが逆です。'),'注意',0);
result := false;
exit;
end;
end;
// 参考値の関数
function f(x: double):double;
begin
// 参考値をx^3とx^5で作成すると、補間計算がn次計算となるので誤差がでません。
result := 0;
case Form1.RadioGroup2.ItemIndex of
0 : result := x - power(x,3) / 5 + power(x,5) / 100;
1 : result := ln(x);
2 : result := 1 / (1 + 2 * x * x);
end;
end;
// 参考値 セット
procedure TForm1.testdataBtnClick(Sender: TObject);
var
N, ch : integer;
i : integer;
x, y : Darray;
d, dx, minx, maxx : double;
begin
N := Ninput;
if N < 0 then exit;
val(MinXedit.Text, minx, ch);
if ch <> 0 then begin
application.MessageBox('Min値の入力に間違いが有ります。','注意',0);
exit;
end;
val(MaxXedit.Text, maxx, ch);
if ch <> 0 then begin
application.MessageBox('Max値の入力に間違いが有ります。','注意',0);
exit;
end;
if minx >= maxx then begin
application.MessageBox('Max値の値がMin値より小さな値です。','注意',0);
exit;
end;
Nedit.Text := inttostr(N);
GridSet(N + 1, 3);
setlength(x, N);
setlength(y, N);
Series1.Clear;
Series2.Clear;
Series3.Clear;
Series4.Clear;
dx := (maxx - minx) / (N- 1);
for i := Low(x) to High(x) do begin
d := i * dx + minx;
if radiogroup2.ItemIndex = 1 then d := d - minx + 0.1;
x[i] := d;
y[i] := f(d);
end;
for i := 0 to N - 1 do begin
StringGrid1.cells[1,i + 1] := floatTostr(x[i]);
StringGrid1.cells[2,i + 1] := floatTostr(y[i]);
end;
DEF := True; // 差分グラフ表示フラグ
interpolationBtnClick(Nil);
end;
// ネヴィル補間計算
function neville(d: Double; x: DArray; y: DArray): Double;
var
w : array of array of double;
i, j : integer;
begin
setlength(w, high(x) + 1, high(y) + 1);
for i := Low(x) to High(x) do w[0,i] := y[i];
for j := 1 to High(x) do begin
for i := Low(x) to (High(x) - j) do
w[j,i] := w[j-1,i+1] + (w[j-1,i+1] - w[j-1,i]) * (d - x[i+j]) / (x[i+j] - x[i]);
end;
result := w[high(x),0];
end;
// エイトケン補間計算
function aitken(d: Double; x: DArray; y: DArray): Double;
var
i, j : integer;
w : DArray;
begin
setlength(w, High(x) + 1);
for i := Low(x) to High(x) do w[i] := y[i];
for j := 1 to High(x) do
for i := High(x) downto j do
w[i] := (w[i-1] * (x[i] - d) - w[i] * (x[i-j] - d)) / (x[i] - x[i-j]);
result := w[High(x)];
end;
// ラグランジェ補間計算
function Lagrange( xx: double; x, y: DArray): double;
var
i, j : integer;
s, p : double;
begin
s := 0;
for i := Low(x) to High(x) do begin
p := y[i];
for j := Low(x) to High(x) do begin
if i <> j then
p := p * (xx - x[j]) / (x[i] - x[j]);
end;
s := s + p;
end;
result := s;
end;
// グリッドの値による補間計算
procedure TForm1.interpolationBtnClick(Sender: TObject);
var
N, ch, i, imax : integer;
cn : string;
y2, y3 : double;
xx : double;
begin
Xin_interpolation.Enabled := False;
N := Ninput;
if N < 0 then exit;
GridSet(N + 1, 3);
setlength(x, N);
setlength(y, N);
for i := Low(x) to High(x) do begin
val(StringGrid1.cells[1,i + 1], x[i], ch);
if ch <> 0 then begin
cn := 'x' + intTostr(i + 1) + 'に間違いが有ります。';
application.MessageBox(pchar(cn),'注意',0);
break;
end;
val(StringGrid1.cells[2,i + 1], y[i], ch);
if ch <> 0 then begin
cn := 'y' + intTostr(i + 1) + 'に間違いが有ります。';
application.MessageBox(pchar(cn),'注意',0);
break;
end;
end;
if ch <> 0 then exit;
if not datacheck(x, N) then exit; // xの値に重複が無いか確認
Series1.Clear; // プロット値
Series2.Clear; // テスト計算値
Series3.Clear; // 補間値
Series4.Clear; // テスト値と補間値差分
Series5.Clear; // 指定点計算値
chart1.Title.Text.Clear;
case radiogroup1.ItemIndex of
0 : chart1.Title.Text.Append('Nevilles interpolation ');
1 : chart1.Title.Text.Append('aitken interpolation');
2 : chart1.Title.Text.Append('Lagrange interpolation');
end;
xmin := x[0];
xmax := x[0];
for i := Low(x) to High(x) do begin
if x[i] > xmax then xmax := x[i];
if x[i] < xmin then xmin := x[i];
Series1.AddXY(x[i], y[i]);
end;
imax := (N - 1) * 20; // 分割数
dx := (xmax - xmin) / imax;
y3 := 0;
for i := 0 to imax do begin
xx := i * dx + x[0];
case radiogroup1.ItemIndex of
0 : y3 := neville(xx, x, y);
1 : y3 := aitken(xx, x, y);
2 : y3 := Lagrange(xx, x, y);
end;
Series3.AddXY(xx, y3);
if DEF then begin
if radiogroup2.ItemIndex = 1 then xx := xx - xmin + 0.1;
y2 := f(xx);
Series2.AddXY(xx, y2); // テスト値
Series4.AddXY(xx, y3 - y2); // 差分値 差分値-テスト値
end;
end;
DEF := False;
Xin_interpolation.Enabled := True;
end;
// 指定値からの計算 指定値xによるy補間値計算とグラフ表示
procedure TForm1.Xin_interpolationClick(Sender: TObject);
var
ch, i, j : integer;
xd, y1, y3, xx, gmin, gmax: double;
begin
val(Xedit.Text, xd, ch);
if ch <> 0 then begin
application.MessageBox('xからY推定の入力に間違いが有ります。','注意',0);
exit;
end;
Series2.Clear; // テスト値グラフ
Series3.Clear; // 補間値グラフ
Series4.Clear; // 差分値
Series5.Clear; // 指定値点
chart1.Title.Text.Clear;
case radiogroup1.ItemIndex of
0 : chart1.Title.Text.Append('Nevilles interpolation ');
1 : chart1.Title.Text.Append('aitken interpolation');
2 : chart1.Title.Text.Append('Lagrange interpolation');
end;
gmin := xmin;
gmax := xmax;
if xd < gmin then gmin := xd;
if xd > gmax then gmax := xd;
// 最小最大区間グラフ再描画
i := round((gmax - gmin) / dx);
y3 := 0;
for j := 0 to i do begin
xx := j * dx + gmin;
case radiogroup1.ItemIndex of
0 : y3 := neville(xx, x, y);
1 : y3 := aitken(xx, x, y);
2 : y3 := Lagrange(xx, x, y);
end;
Series3.AddXY(xx, y3);
end;
// 指定値点グラフ追加 指定値xによるy補間値計算とグラフ表示
y1 := 0;
case radiogroup1.ItemIndex of
0 : y1 := neville(xd, x, y);
1 : y1 := aitken(xd, x, y);
2 : y1 := Lagrange(xd, x, y);
end;
Series5.AddXY(xd, y1);
end;
// グリッド初期設定
procedure TForm1.FormCreate(Sender: TObject);
begin
FGridSet(101, 3); // 固定行1列1 + 100行2列まで行列を変更しても
// 入力値がクリアされないようにします。
GridSet(4, 3); // 最初の設定
end;
end.
![]() Nevilles_algorithm.zip
Nevilles_algorithm.zip
三角関数、逆三角関数、その他関数 に戻る