2020/02/07
第一二種の楕円積分のｍの値がマイナスの時の計算に間違いがあったので修正しました。
計算結果が正しいことは、分割積分で確認しました。
2020/01/07
第二種楕円積分のK = 1の時とK > 1の時の計算にミスが有ったので修正しました。
cn-, dn-について、ｘ = 1＆ｋ = 1の時、ゼロにならないのを修正しました。
ヤコビのｓｎ－、ｃｎ－、ｄｎ－関数
ヤコビのｓｎ－、ｃｎ－、ｄｎ－関数の計算プログラムです。
Mathematics Source Library C & ASM にあるプログラムをＤｅｌｐｈｉ用に変換したものです。
ｓｎ－，ｃｎ－，ｄｎ－の詳細については ヤコビの楕円関数を参照してください。
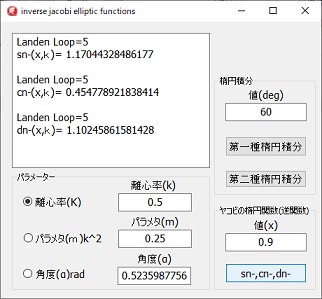ｓｎ－の計算は、第一種不完全楕円積分の計算です。
ｋの値は、積分できる範囲であれば、此処では１を超えても、変換可能です。
パラメタｍの場合は、マイナスの値でも可能です。
αの単位はRadでK=sin(α)となり、ｋの値は１を超えることはありません。
ｓｎ－、ｃｎ－、ｄｎ－の計算をする場合は、値（ｘ）を使用します、第一、二楕円積分の場合は、値(deg)です。
ｘの値は、１より大きくとることは出来ません、ｓｎの値はｓｉｎ(φ)で１を超えることが無い為です。
degの入力の値に制限はありません。
入力値をｄｅｇにしているのは、単に角度を分かりやすくするためです。
第二種不完全積分の計算は、ｓｎ－、ｃｎ－、ｄｎ－の計算には必要ないのですが、参考としてとりあげています。
楕円積分については、此処での計算方式とは違うやり方の方法が既に取り上げてありますが、此処での計算が一番高速で計算出来ます。
第二種楕円積分のランデン変換には、第一種楕円積分も含まれています。
プログラム
unit main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls;
type
TForm1 = class(TForm)
Memo1: TMemo;
GroupBox1: TGroupBox;
a_Edit: TLabeledEdit;
mRadioButton: TRadioButton;
aRadioButton: TRadioButton;
m_Edit: TLabeledEdit;
K_Edit: TLabeledEdit;
kRadioButton: TRadioButton;
GroupBox2: TGroupBox;
secondBtn: TButton;
FirstBtn: TButton;
Deg_Edit: TLabeledEdit;
GroupBox3: TGroupBox;
snukbtn: TButton;
x_Edit: TLabeledEdit;
procedure snukbtnClick(Sender: TObject);
procedure FirstBtnClick(Sender: TObject);
procedure secondBtnClick(Sender: TObject);
private
{ Private 宣言 }
function datainput(var arg, sarg: char;var x, param: double; FE: boolean): boolean;
public
{ Public 宣言 }
end;
function Inverse_Jacobi_sn(x: double; arg: char; param: double; var errF: byte): double;
function Inverse_Jacobi_cn(x: double; arg: char; param: double; var errF: byte): double;
function Inverse_Jacobi_dn(x: double; arg: char; param: double; var errF: byte): double;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses
system.Math, First_kind, second_kind;
procedure parameter(arg: char; x: double; var k, m: double);
begin
case arg of
'a': begin
k := sin(x);
m := k * k;
end;
'm': begin
m := x;
k := sqrt(abs(m));
end;
else begin
k := abs(x);
m := k * k;
end;
end;
end;
function Inverse_Jacobi_cd(x, k: double; var errF: byte): double;
var
m, phi: double;
begin
m := k * k;
result := 0;
if (m > 0) and (m < 1) then begin
phi := (1 - m) / (1 - m * x * x);
if phi < 0 then begin
errF := 3;
exit;
end;
phi := x * sqrt(phi);
if abs(phi) > 1 then begin
errF := 3;
exit;
end;
phi := arccos(phi);
result := Legendre_Elliptic_Integral_First_Kind(phi, 'k', k);
exit;
end;
if m = 0 then begin
if abs(x) > 1 then begin
errF := 1;
exit;
end;
result := arccos(x);
exit;
end;
end;
function Inverse_Jacobi_sd(x, k: double; var errF: byte): double;
var
m, phi: double;
begin
result := 0;
m := k * k;
if (m > 0) and (m < 1) then begin
phi := x / sqrt(1 + m * x * x );
if abs(phi) > 1 then begin
errf := 3;
exit;
end;
phi := arcsin(phi);
result := Legendre_Elliptic_Integral_First_Kind(phi, 'k', k);
exit;
end;
if m = 0 then begin
if abs(x) > 1 then begin
errF := 1;
exit;
end;
result := arcsin(x)
end
else begin
result := arcsinh(x);
end;
end;
function Inverse_Jacobi_nd(x, k: double; var errF: byte): double;
begin
result := Inverse_Jacobi_dn(1 / x, 'k', k, errF);
end;
function Inverse_Jacobi_dn(x: double; arg: char; param: double; var errF: byte): double;
var
k, m, kp, phi: double;
begin
result := 0;
errF := 0;
if x < 0 then begin
errF := 5;
exit;
end;
parameter(arg, param, k, m);
if (m > 0) and (m < 1) then begin
phi := 1 - x * x;
if phi < 0 then begin
errF := 1;
exit;
end;
phi := sqrt(phi) / abs(k);
if phi > 1 then begin
errF := 2;
exit;
end;
phi := arcsin(phi);
result := Legendre_Elliptic_Integral_First_Kind(phi, 'k', k);
exit;
end;
if m = 0 then begin
result := 0;
exit;
end;
if m = 1 then begin
if abs(x) > 1 then begin
errF := 1;
exit;
end;
result := arcsech(x);
exit;
end;
if m > 1 then begin
result := Inverse_Jacobi_cn(x, 'k', 1 / k, errF) / k;
exit;
end;
kp := sqrt(1 - m);
result := Inverse_Jacobi_nd(x, k / kp, errF) / kp;
if errF = 1 then errF := 4;
if errF = 2 then errF := 3;
end;
function Inverse_Jacobi_sn(x: double; arg: char; param: double; var errF: byte): double;
var
k, m, kp, phi : double;
begin
errF := 0;
result := 0;
parameter(arg, param, k, m);
if (m > 0) and (m < 1) then begin
if abs(x) > 1 then begin
errF := 1;
exit;
end;
phi := arcsin(x);
result := Legendre_Elliptic_Integral_First_Kind(phi, 'k', k);
exit;
end;
if (m = 0) then begin
if abs(x) > 1 then begin
errF := 1;
exit;
end;
result := arcsin(x);
exit;
end;
if m = 1 then
if x = -1 then begin
result := -infinity;
exit;
end
else
if x = 1 then begin
result := infinity;
exit;
end
else begin
if abs(x) > 1 then begin
errF := 1;
exit;
end;
result := arctanh(x);
exit;
end;
if m > 1 then begin
result := Inverse_Jacobi_sn(k * x, 'k', 1 / k, errF) / k;
exit;
end;
kp := sqrt(1 - m);
result := Inverse_Jacobi_sd(kp * x, k / kp, errF) / kp;
end;
function Inverse_Jacobi_cn(x: double; arg: char; param: double; var errF: byte): double;
var
k, m, kp, phi: double;
begin
errF := 0;
result := 0;
if x < 0 then begin
errF := 5;
exit;
end;
parameter(arg, param, k, m);
if (m > 0) and (m < 1) then begin
if abs(x) > 1 then begin
errF := 1;
exit;
end;
phi := arccos(x);
result := Legendre_Elliptic_Integral_First_Kind(phi, 'k', k);
exit;
end;
if m = 0 then begin
if abs(x) > 1 then begin
errF := 1;
exit;
end;
result := arccos(x);
exit;
end;
if m = 1 then begin
if abs(x) > 1 then begin
errF := 1;
exit;
end;
result := arcsech(x);
exit;
end;
if m > 1 then begin
result := Inverse_Jacobi_dn(x, 'k', 1.0 / k, errF) / k;
exit;
end;
kp := sqrt(1 - m);
result := Inverse_Jacobi_cd(x, k / kp, errF) / kp;
end;
function TForm1.datainput(var arg, sarg: char; var x, param: double; FE: boolean): boolean;
var
ch : integer;
begin
result := false;
arg := '0';
sarg := ' ';
if kradiobutton.Checked then begin
arg := 'k';
sarg := 'ｋ';
end;
if mradiobutton.Checked then begin
arg := 'm';
sarg := 'ｍ';
end;
if aradiobutton.Checked then begin
arg := 'a';
sarg := 'α';
end;
if FE then val(Deg_edit.text, x, ch)
else val(x_edit.text, x, ch);
if ch <> 0 then begin
application.MessageBox('Ｘの値に間違いがあります。','注意',0);
exit;
end;
param := 0;
if kradiobutton.Checked then begin
val(k_edit.Text, param, ch);
if ch <> 0 then begin
application.MessageBox('離心率(k)に間違いがあります。','注意', 0);
exit;
end;
end;
if mradiobutton.Checked then begin
val(m_edit.Text, param, ch);
if ch <> 0 then begin
application.MessageBox('パラメーター(m)に間違いがあります。','注意', 0);
exit;
end;
end;
if aradiobutton.Checked then begin
val(a_edit.Text, param, ch);
if ch <> 0 then begin
application.MessageBox('Radian(α)に間違いがあります。','注意', 0);
exit;
end;
end;
result := true;
end;
procedure TForm1.snukbtnClick(Sender: TObject);
var
x, param, snmu: double;
cnmu, dnmu: double;
arg, sarg: char;
errF: byte; // 0: ok 1: x の値大 2: x or k,m 小 3 x 大 or m小 4 x 小
begin
if not datainput(arg, sarg, x, param, False) then exit;
memo1.Clear;
snmu := Inverse_Jacobi_sn(x, arg, param, errF);
case errF of
1 : memo1.Lines.Add('sn-(x,' + sarg +')= ｘの値大');
3 : memo1.Lines.Add('sn-(x,' + sarg +')= ｘの値大 又は' + sarg + 'の絶対値が小');
0 : memo1.Lines.Add('sn-(x,' + sarg +')= ' + floatTostr(snmu));
end;
memo1.Lines.Add('');
cnmu := Inverse_Jacobi_cn(x, arg, param, errF);
case errF of
1 : memo1.Lines.Add('cn-(x,' + sarg +')= ｘの値大');
2 : memo1.Lines.Add('cn-(x,' + sarg +')= ｘの値 又は' + sarg + 'の絶対値小');
3 : memo1.Lines.Add('cn-(x,' + sarg +')= ｘの値大 又は' + sarg + 'の絶対値が小');
5 : memo1.Lines.Add('cn-(x,' + sarg +')= ｘの値にマイナスはありません。');
0 : memo1.Lines.Add('cn-(x,' + sarg +')= ' + floatTostr(cnmu));
end;
memo1.Lines.Add('');
dnmu := Inverse_Jacobi_dn(x, arg, param, errF);
case errF of
1 : memo1.Lines.Add('dn-(x,' + sarg +')= ｘの値大');
2 : memo1.Lines.Add('dn-(x,' + sarg +')= ｘの値 又は' + sarg + 'の絶対値小');
3 : memo1.Lines.Add('dn-(x,' + sarg +')= ｘの値大 又は' + sarg + 'の絶対値が小');
4 : memo1.Lines.Add('dn-(x,' + sarg +')= ｘの値小 又は' + sarg + 'の絶対値が小');
5 : memo1.Lines.Add('dn-(x,' + sarg +')= ｘの値にマイナスはありません。');
0 : memo1.Lines.Add('dn-(x,' + sarg +')= ' + floatTostr(dnmu));
end;
end;
procedure TForm1.FirstBtnClick(Sender: TObject);
var
x, F : double;
param, k, m: double;
arg, sarg: char;
begin
if not datainput(arg, sarg, x, param, True) then exit;
memo1.Clear;
memo1.Lines.Add('第一種楕円積分');
parameter(arg, param, k, m);
if m > 1 then begin
F := arcsin(sqrt(1 / m));
F := F / pi * 180;
memo1.Lines.Add('積分角度の上限＝' + floattostr(F));
if abs(x) > F then begin
memo1.Lines.Add('積分角度の範囲を超えています');
exit;
end;
end;
x := x / 180 * pi;
F := Legendre_Elliptic_Integral_First_Kind(x, arg, param);
memo1.Lines.Add('F(x,' + sarg +')= ' + floatTostr(F));
end;
procedure TForm1.secondBtnClick(Sender: TObject);
var
x, E : double;
param, k, m: double;
arg, sarg: char;
begin
if not datainput(arg, sarg, x, param, True) then exit;
memo1.Clear;
memo1.Lines.Add('第二種楕円積分');
parameter(arg, param, k, m);
if m > 1 then begin
E := arcsin(sqrt(1 / m));
E := E / pi * 180;
memo1.Lines.Add('積分角度の上限＝' + floattostr(E));
if abs(x) > E then begin
memo1.Lines.Add('積分角度の範囲を超えています');
exit;
end;
end;
x := x / 180 * pi;
E := Legendre_Elliptic_Integral_Second_Kind(x, arg, param);
memo1.Lines.Add('E(x,' + sarg +')= ' + floatTostr(E));
end;
end.
unit First_kind; interface function Legendre_Elliptic_Integral_First_Kind(amplitude: double; arg: char; x: double): double; implementation uses system.Math, main, System.SysUtils; const PI_2 = pi / 2; // ランデン変換第一種積分 procedure Landen_Transform(phi, parameter: double; var K, F: double); const EPSILON = 1E-12; var two_n : double; a, g : double; a_old : double; g_old : double; tan_phi : double; N : integer; begin N := 0; two_n := 1; a := 1; g := sqrt(1.0 - parameter); while true do begin tan_phi := tan(phi); two_n := two_n + two_n; phi := phi + phi - arctan((a - g) * tan_phi / (a + g * tan_phi * tan_phi)); g_old := g; a_old := a; a := (g_old + a_old) / 2; g := sqrt(g_old * a_old); inc(N); if abs(a_old - g_old) <= (a_old * EPSILON) then break; // if a_old - g_old = 0 then break; end; phi := phi / two_n; F := phi / g; K := PI_2 / g; Form1.Memo1.Lines.Add('Landen Loop=' + intTostr(N)); end; // mの値が1を超える場合の積分処理 function Large_Modulus(amplitude, k : double): double; var F, Kl : double; phi : double; sin_phi: double; n : integer; begin phi := amplitude; n := trunc((phi + PI_2) / PI); phi := phi - n * PI; n := n + n; sin_phi := sin(phi); if abs(sin_phi) >= 1 / k then begin if phi > 0 then phi := PI_2 else phi := -PI_2; end else phi := arcsin(k * sin_phi); Landen_Transform(abs(phi), 1 / (k * k) , Kl, F); if phi >= 0 then F := F + n * Kl else F := n * Kl - F; result := F / k; end; // 第一種楕円積分処理 積分範囲を制限なしに拡大します // K 完全積分 // F 不完全積分 // phi rad単位 procedure Elliptic_Integral_First_Kind(phi, m: double; var K, F: double); var n : integer; begin n := trunc((phi + PI_2) / PI); phi := phi - n * PI; n := n + n; Landen_Transform(abs(phi), m, K, F); if phi >= 0 then F := F + n * K else F := n * K - F; end; // ルジャンドルの第一種楕円積分 function Legendre_Elliptic_Integral_First_Kind(amplitude: double; arg: char; x: double):double; var phi : double; k, m : double; Kl, F : double; sgn_amplitude : integer; begin sgn_amplitude := sign(amplitude); if amplitude = 0 then begin result := 0; exit; end; if x = 0 then begin result := sgn_amplitude; exit; end; case arg of 'k': begin k := abs(x); m := k * k; end; 'm': begin m := x; k := sqrt(abs(m)); end; 'a': begin k := abs(sin(x)); m := k * k; end; else begin k := abs(x); m := k * k; end; end; if (m > 0) and (m < 1) then begin Elliptic_Integral_First_Kind(amplitude, m, Kl, F); result := F; exit; end; if m < 0 then begin phi := abs(amplitude); Elliptic_Integral_First_Kind(abs(PI_2 - phi), abs(m / (1 - m)), Kl, F); // phi := PI_2 - abs(amplitude); // Elliptic_Integral_First_Kind(abs(phi), abs(m / (1 - m)), Kl, F); if phi > PI_2 then begin result := sgn_amplitude * (Kl + F) / sqrt(1 - m); exit; end else begin result := sgn_amplitude * (Kl - F) / sqrt(1 - m); exit; end; end; if m = 1 then begin if abs(amplitude) >= PI_2 then begin result := sgn_amplitude * Infinity; exit; end; x := tan(amplitude); result := sgn_amplitude * (ln(abs(x) + sqrt(1 + x * x))); exit; end; // case m > 1 result := Large_Modulus(amplitude, k); end; end.
unit second_kind; interface function Legendre_Elliptic_Integral_Second_Kind(amplitude: double; arg: char; x: double): double; implementation uses System.math, main, System.SysUtils; const PI_4 = PI / 4; PI_2 = PI / 2; // ランデン変換第一種二種積分 procedure Landen_Transform(phi, parameter: double; var F, Fk, E, Ek: double); const EPSILON = 1E-12; var two_n : double; a : double; g : double; a_old : double; g_old : double; tan_phi : double; sum : double; integral: double; N : integer; begin two_n := 1; g := sqrt(1 - parameter); a := 1; sum := 2 * (2 - parameter); integral := 0; N := 0; while true do begin tan_phi := tan(two_n * phi); sum := sum - two_n * (a - g) * (a - g); two_n := two_n + two_n; phi := phi - arctan((a - g) * tan_phi / (a + g * tan_phi * tan_phi) ) / two_n; integral := integral + (a - g) * sin(two_n * phi); g_old := g; a_old := a; a := (g_old + a_old) / 2; g := sqrt(g_old * a_old); inc(N); if abs(a_old - g_old) <= (a_old * EPSILON) then break; // if a_old - g_old = 0 then break; end; F := phi / g; Fk := PI_2 / g; E := integral / 2 + sum / 4 * phi / g; Ek := PI_4 / a * sum / 2; Form1.Memo1.Lines.Add('Landen Loop=' + intTostr(N)); end; // mの値が1を超える場合の積分処理 function Large_Modulus(amplitude, kp: double): double; var F, K, E, Ek : double; phi : double; sin_phi : double; n : integer; begin phi := amplitude; n := Trunc((phi + PI_2) / PI); phi := phi - n * PI; n := n + n; sin_phi := sin(phi); if abs(sin_phi) >= 1 / kp then begin if phi > 0 then phi := PI_2 else phi := -PI_2; end else phi := arcsin(kp * sin_phi); Landen_Transform(abs(phi), 1 / (kp * kp) , F, K, E, Ek); Ek := kp * Ek + (1 - kp * kp) * K / kp; E := kp * E + (1 - kp * kp) * F / kp; if phi >= 0 then E := E + n * Ek else E := n * Ek - E; result := E; end; // 第二種楕円積分処理 積分範囲を制限なしに拡大します // Em 完全積分 // Em_phi 不完全積分 // phi rad単位 procedure Elliptic_Integral_Second_Kind(phi, m: double; var Em, Em_phi: double); var F, Fk : double; n : integer; begin n := trunc((phi + PI_2 )/ PI); phi := phi - n * PI; n := n + n; Landen_Transform(abs(phi), m, F, Fk, Em_phi, Em); if phi >= 0 then Em_phi := Em_phi + n * Em else Em_phi := n * Em - Em_phi; end; // ルジャンドルの第二種楕円積分 function Legendre_Elliptic_Integral_Second_Kind(amplitude: double; arg: char; x: double): double; var phi : double; k, m : double; Em, Em_phi : double; n : integer; sgn_amplitude : integer; begin sgn_amplitude := sign(amplitude); if amplitude = 0 then begin result := 0; exit; end; if x = 0 then begin result := amplitude; exit; end; case arg of 'k': begin k := abs(x); m := k * k; end; 'm': begin m := x; k := sqrt(abs(m)); end; 'a': begin k := sin(x); m := k * k; end; else begin k := abs(x); m := k * k; end; end; if (m > 0) and (m < 1) then begin Elliptic_Integral_Second_Kind(amplitude, m, Em, Em_phi); result := Em_phi; exit; end; if m < 0 then begin phi := abs(amplitude); Elliptic_Integral_Second_Kind(abs(PI_2 - phi), abs(m / (1 - m)), Em, Em_phi); // phi := PI_2 - abs(amplitude); // Elliptic_Integral_Second_Kind(abs(phi), abs(m / (1 - m)), Em, Em_phi); if phi > PI_2 then result := sgn_amplitude * (Em + Em_phi) * sqrt(1 - m) else result := sgn_amplitude * (Em - Em_phi) * sqrt(1 - m); exit; end; if m = 1 then begin phi := abs(amplitude); if phi <= PI_2 then begin result := sin(amplitude); exit; end; n := trunc((phi + PI_2) / PI); n := n + n; result := sgn_amplitude * (n + sin(phi - n * PI)); exit; end; // case m > 1 result := Large_Modulus(amplitude, k); end; end.
inverse_jacobi_elliptic_functions.zip