2020/05/11
StopWatch コンポーネントを不要にしました。
2020/02/01
StopWatch コンポーネントをダウンロード出来るようにしました。
Delphi標準のStopWatchでは、時間が短すぎて、測定が出来ないのでWtopWatchコンポーネントを追加しています。
>ヤコビの楕円関数の検討
縄跳びの紐の形が、ヤコビの楕円関数で現されるので、これについて、プログラムを検討してみました。
最初は、第一種楕円積分の逆関数なので、第一種楕円積分を利用して、sn(u,k)の計算プログラムを作成してみましたが、あまりにも時間がかかるので、色々探して、テストをしてみました。
第一種楕円積分の計算をそのまま利用したものは、計算の結果に間違いがないので、検算用に利用しています。
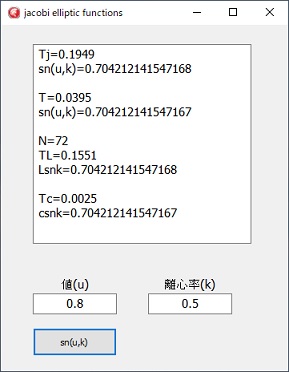T=は、実行時間です、単位は秒です。
一番上は、カールソンの第一種楕円積分を利用して、逆算をしたものです。
二番目は、Wikipediaに有ったランベルト級数による計算。
三番目は、ランデン変換による第一種楕円積分による逆算です。
四番目は、Mathematics Source Library C & ASMにあるヤコビの楕円関数をDelphi用に変換したものです。
計算時間は、圧倒的に四番目のelliptic amplitude function、Gaussian transformationsを使用した計算が速くなっています。
プログラムも簡単です。
二番目のランベルト級数による計算は、離心率の値が0.0001と小さくなると、計算の誤差が大きくなりますが実用上は問題ないと思われます。
計算の精度は、Ｄｏｕｂｌｅとしました。
テストプログラム
//----------------------------------------------------- // ヤコビの楕円関数 //----------------------------------------------------- unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls, VclTee.TeeGDIPlus, VCLTee.TeEngine, VCLTee.Series, VCLTee.TeeProcs, VCLTee.Chart, StopWatch; type TForm1 = class(TForm) Memo1: TMemo; snukbtn: TButton; u_Edit: TLabeledEdit; K_Edit: TLabeledEdit; StopWatch1: TStopWatch; procedure snukbtnClick(Sender: TObject); private FFrequency: int64; // ストップウォッチ用 基準クロック FStart: int64; // スタートカウンター値 FStop: int64; // ストップカウンター値 { Private 宣言 } function RF(x1, y1, z1: double): double; function calc_first_elliptic_integral(k, sinQ: double): double; function jacobi_sn(u, k: double): double; function KKd_jacobi_sn(u, k: double): double; function first_imperfect_elliptic_integral(Q, K: double): double; function Lanjacobi_sn(u, k: double): double; function Lcalc_first_elliptic_integral(k, sinQ: double): double; procedure Start; // stopwatch strat function Stop: extended; // stopwatch stop public { Public 宣言 } end; var Form1: TForm1; implementation {$R *.dfm} uses Math; // ストップウォッチスタート procedure TForm1.Start; begin QueryPerformanceFrequency(FFrequency); // 基準クロック取得 QueryPerformanceCounter(FStart); // スタート時カウンター値 end; // ストップウォッチ停止 function TForm1.Stop: extended; begin QueryPerformanceCounter(FStop); // ストップ時カウンター時 if FFrequency > 0 then // クロックの値を取得出来ていたら時間計算 result := (FStop - FStart) * 1000 / FFrequency else result := -1; end; //------------------------------- // 第１種不完全積分 // FBnKn[0] 第１種不完全積分解 // ランデン変換 // Q 角度 rad // K 離心率 //------------------------------- function TForm1.first_imperfect_elliptic_integral(Q, K: double): double; var I, MI : integer; Kn : array of double; // Kn knd : array of double; // k'n N2SKn : array of double; // 2/(1+Kn) T2SKnd : array of double; // П2/(1+Kn') BRad : array of double; // β(rad) SinBn : array of double; // sinβn FBnKn : array of double; // F(βn,kn) LnD : double; begin // K = 0 の時は円なのでpiの角度値rad。 if K = 0 then begin result := Q; exit; end; // この時は1をかえします。 if (K = 1) and (Q = pi / 2) then begin result := 1; exit; end; // 1 >= K > 0 の時 MI := 0; LnD := 0; setlength(kn, MI + 1); // kn kn[0] := K; while LnD <> Kn[MI] do begin // LnDとkn[]が同じ１になるまでくり返します LnD := Kn[MI]; inc(MI); setlength(kn, MI + 1); // kn kn[MI] := 2 * sqrt(Kn[MI - 1])/(1 + Kn[MI - 1]); end; setlength(kn, MI); // kn setlength(knd, MI); // k'n setlength(N2SKn, MI); // 2/(1+Kn) setlength(T2SKnd, MI); // П2/(1+Kn') setlength(BRad, MI); // β(rad) setlength(SinBn, MI); // sinβn setlength(FBnKn, MI); // F(βn,kn) dec(MI); knd[0] := 1; for I := 1 to MI do knd[I] := (1 - kn[I - 1]) / (1 + Kn[I - 1]); for I := 0 to MI do N2SKn[I] := 2 / (1 + kn[I]); T2SKnd[MI] := N2SKn[MI]; for I := MI - 1 downto 0 do T2SKnd[I] := T2SKnd[I + 1] * N2SKn[I]; BRad[0] := Q; for I := 1 to MI do BRad[I] := (arcsin(kn[I - 1] * sin(Brad[I - 1])) + Brad[I - 1]) / 2; for I := 0 to MI do SinBn[I] := sin(Brad[I]); result := (1 + sin(Brad[MI])) / cos(Brad[MI]); if result <= 0 then exit; // 0以下は自然対数の計算出来ません LnD := LN(result); result := T2SKnd[0] * LnD; // 第一種 end; // 第一種楕円積分 ルーチン // 積分範囲制限なし sin(π/2) = 1 単位積分 function TForm1.Lcalc_first_elliptic_integral(k, sinQ: double): double; var J : integer; k2 : double; fqk : double; f1k : double; fek : double; asin : double; begin asin := abs(sinQ); k2 := k * k; // k^2 if (k2 >= 1) and (asin >= 1) then begin // 積分出来ない値だったら if sinQ > 0 then result := MaxDouble // double最大値セット∞の代わり else result := -MaxDouble; // double最小値セット-∞の代わり exit; // 終了 end; f1k := 0; // 完全積分値初期化 J := trunc(asin); // 整数部取り出し if J mod 2 = 0 then asin := asin - J // 小数部処理 象限処理 else asin := 1 - (asin - J); if (J <> 0) and (k2 < 1) then f1k := first_imperfect_elliptic_integral(pi / 2, k); // 第一種完全積分 fek := first_imperfect_elliptic_integral(arcsin(asin), k); // 第一種不完全積分 if j mod 2 = 0 then fqk := j * f1k + fek // 第1,第3象限の積分値 else fqk := (j + 1) * f1k - fek; // 第2,第4象限の積分値 if sinQ < 0 then fqk := -fqk; // 積分範囲の符号で積分値の符号設定 result := fqk; end; // ヤコビの楕円関数 sn(u, k) ランデン変換第一種楕円積分による逆計算 function TForm1.Lanjacobi_sn(u, k: double): double; const Keps = 1E-15; KN = 1000; var eps : double; sinQ : double; ud, dsin : double; i : integer; absu : double; N : integer; t : double; begin Start; eps := Keps; absu := abs(u); // uの絶対値 dsin := 0.5; // 初期補正角度設定 sinQ := 0.5; // 初期値設定 for i := 0 to KN do begin ud := Lcalc_first_elliptic_integral(k, sinQ); if ud > absu then begin // 積分値が指定値より大きかったら sinQ := sinQ - dsin; // 補正値減算 dsin := dsin / 2; // 補正値２分の１に end; sinQ := sinQ + dsin; // 補正値加算 if dsin < eps then break; // 角度補正値が収束判定値より小さくなったら終了 end; N := i; i := trunc(sinQ); if i mod 2 = 0 then // sin(90°)単位をsin(180°)単位に変換 sinQ := (sinQ - i) // 奇数象限と偶数象限計算 else sinQ := 1 - (sinQ - i); i := i div 2; // sin(180°)単位をsin(360°)に変換 if i mod 2 <> 0 then sinQ := -sinQ; // sinは180°毎に符号が反転 if u < 0 then sinQ := -sinQ; // 範囲の符号で逆変換値の符号設定 result := sinQ; t := Stop; Memo1.Lines.Add('N=' + intTostr(N)); memo1.Lines.Add('TL=' + floatTostr(t)); end; // Carlson's Elliptic Integral RF function TForm1.RF(x1, y1, z1: double): double; var la, mu : double; x2, y2, z2 : double; x3, y3, z3 : double; s2, s3 : double; r0, rf : double; s22, s23, s2s3, s32 : double; begin rf := 0; repeat r0 := rf; la := sqrt(x1 * Y1) + sqrt(x1 * z1) + sqrt(y1 * z1); mu := (x1 + y1 + z1) / 3; x2 := (x1 + la) / 4; y2 := (y1 + la) / 4; z2 := (z1 + la) / 4; x3 := 1 - x2 / mu; y3 := 1 - y2 / mu; z3 := 1 - z2 / mu; s2 := (x3 * x3 + y3 * y3 + z3 * z3) / 4; s3 := (x3 * x3 * x3 + y3 * y3 * y3 + z3 * z3 * z3) / 6; s22 := s2 * s2 / 6; s23 := 5 * s2 * s2 * s2 / 26; s32 := 3 * s3 * s3 / 26; s2s3 := s2 * s3 * 3 / 11; rf := (1 + s2 / 5 + s3 / 7 + s22 + s2s3 + s23 + s32) / sqrt(mu); x1 := x2; y1 := y2; z1 := z2; until rf = r0; result := rf; end; // 第一種楕円積分 ルーチン // 積分範囲制限なし sin(π/2) = 1 単位積分 function TForm1.calc_first_elliptic_integral(k, sinQ: double): double; var J : integer; s2 : double; c2 : double; rf0 : double; k2 : double; fqk : double; f1k : double; fek : double; asin : double; begin asin := abs(sinQ); k2 := k * k; // k^2 if (k2 >= 1) and (asin >= 1) then begin // 積分出来ない値だったら if sinQ > 0 then result := MaxDouble // double最大値セット∞の代わり else result := -MaxDouble; // double最小値セット-∞の代わり exit; // 終了 end; f1k := 0; // 完全積分値初期化 J := trunc(asin); // 整数部取り出し if J mod 2 = 0 then asin := asin - J // 小数部処理 象限処理 else asin := 1 - (asin - J); if (J <> 0) and (k2 < 1) then f1k := RF(0, 1 - k2, 1); // 第一種完全積分 s2 := asin * asin; // sin~2(φ) c2 := 1 - s2; // cos^2(φ') rf0 := RF(c2, 1 - k2 * s2, 1); fek := asin * rf0; // F(φ',K) = rf0 * sin(φ') 第一種不完全積分 if j mod 2 = 0 then fqk := j * f1k + fek // 第1,第3象限の積分値 else fqk := (j + 1) * f1k - fek; // 第2,第4象限の積分値 if sinQ < 0 then fqk := -fqk; // 積分範囲の符号で積分値の符号設定 result := fqk; end; // ヤコビの楕円関数 sn(u, k) 第一種楕円積分による逆計算 function TForm1.jacobi_sn(u, k: double): double; const Keps = 1E-15; KN = 1000; var eps : double; sinQ : double; ud, dsin : double; i : integer; absu : double; N : integer; t : double; begin Start; eps := Keps; absu := abs(u); // uの絶対値 dsin := 0.5; // 初期補正角度設定 sinQ := 0.5; // 初期値設定 for i := 0 to KN do begin ud := calc_first_elliptic_integral(k, sinQ); // 第一種楕円積分 if ud > absu then begin // 積分値が指定値より大きかったら sinQ := sinQ - dsin; // 補正値減算 dsin := dsin / 2; // 補正値２分の１に end; sinQ := sinQ + dsin; // 補正値加算 if dsin < eps then break; // 角度補正値が収束判定値より小さくなったら終了 end; N := i; i := trunc(sinQ); if i mod 2 = 0 then // sin(90°)単位をsin(180°)単位に変換 sinQ := (sinQ - i) // 奇数象限と偶数象限計算 else sinQ := 1 - (sinQ - i); i := i div 2; // sin(180°)単位をsin(360°)に変換 if i mod 2 <> 0 then sinQ := -sinQ; // sinは180°毎に符号が反転 if u < 0 then sinQ := -sinQ; // 範囲の符号で逆変換値の符号設定 result := sinQ; t := Stop; Memo1.Lines.Add('N=' + intTostr(N)); memo1.Lines.Add('Tj=' + floatTostr(t)); end; // ヤコビ楕円関数 ランベルト級数 function TForm1.KKd_jacobi_sn(u, k: double): double; const KN = 100; var Kl, Kld : double; q, v, kd : double; siguma : double; n : integer; half : double; n2p1 : integer; t : double; begin Start; kd := sqrt(1 - k * k); Kl := calc_first_elliptic_integral(k, 1); Kld := calc_first_elliptic_integral(kd, 1); siguma := 0; q := exp(-pi * Kld / Kl); v := pi * u / (2 * Kl); half := 1 / 2; for n := 0 to KN do begin n2p1 := n + n + 1; siguma := siguma + power(q, n + half) / (1 - power(q, n2p1)) * sin(n2p1 * v); end; if k > 1E-5 then result := 2 * pi / Kl / K * siguma else result := sin(u); // kの値が小さくなると誤差が大きくなるので単にsinで計算 t := Stop; // memo1.Lines.Add('K =' + floatTostr(KL)); // memo1.Lines.Add('K''=' + floatTostr(KLd)); memo1.Lines.Add('T=' + floatTostr(t)); end; // 振幅関数 function Jacobi_am(u: double; arg: char; x: double): double; const KN = 30; EPSILON = 1E-15; var a: array of double; g: array of double; c: array of double; two_n : double; phi : double; k : double; i, j, N : integer; half : double; begin if x = 0 then begin result := u; exit; end; case arg of 'a' : k := sin(abs(x)); 'm' : k := sqrt(abs(x)); else k := abs(x); end; if k = 1 then begin result := 2 * arctan(exp(u)) - pi / 2; exit; end; N := 1; setlength(a, N); setlength(g, N); setlength(c, N); a[0] := 1; g[0] := sqrt(1 - k * k); c[0] := k; two_n := 1; half := 1 / 2; for i := 0 to KN do begin if abs(a[i] - g[i]) < a[i] * EPSILON then break; two_n := two_n + two_n; inc(N); setlength(a, N); setlength(g, N); setlength(c, N); a[i + 1] := half * (a[i] + g[i]); g[i + 1] := sqrt(a[i] * g[i]); c[i + 1] := half * (a[i] - g[i]); end; phi := two_n * a[i] * u; for j := i downto 1 do phi := half * (phi + arcsin(c[j] * sin(phi) / a[j])); result := phi; end; // ヤコビ楕円関数 function c_jacobi_sn(u: double; arg: char; x: double):double; var t : double; begin Form1.Start; result := sin(Jacobi_am(u, arg, x)); t := Form1.Stop; Form1.Memo1.Lines.Add('Tc=' + floatTostr(t)); end; // sn(u,k)計算 procedure TForm1.snukbtnClick(Sender: TObject); var k, u, snuk : double; KKd_snuk : double; Lsnuk : double; csnu : double; ch : integer; begin val(k_edit.Text, k, ch); if ch <> 0 then begin application.MessageBox('離心率(k)に間違いがあります。','注意',0); exit; end; if K > 1 then begin application.MessageBox('離心率(k)は１以下にして下さい。','注意',0); exit; end; val(u_edit.Text, u, ch); if ch <> 0 then begin application.MessageBox('値(u)に間違いがあります。','注意',0); exit; end; memo1.Clear; snuk := jacobi_sn(u, k); memo1.Lines.Add('sn(u,k)=' + floatTostr(snuk)); memo1.Lines.Add(''); if K < 1 then begin KKd_snuk := KKd_jacobi_sn(u, k); memo1.Lines.Add('sn(u,k)=' + floatTostr(KKD_snuk)); end else memo1.Lines.Add('KKd_jacobi_sn K=1 不可'); memo1.Lines.Add(''); Lsnuk := Lanjacobi_sn(u, k); memo1.Lines.Add('Lsnk=' + floatTostr(Lsnuk)); memo1.Lines.Add(''); csnu := c_jacobi_sn(u, 'K', k); memo1.Lines.Add('csnk=' + floatTostr(csnu)); end; end.
jacobi_elliptic_KKd_function.zip