楕円積分の逆変換
第一、二、三種楕円積分の逆変換について検討してみました。
ヤコビの楕円関数SNがあるのですか、これは、第一種楕円積分の逆変換と同じになっているのですが、値の範囲は、-1～1の範囲に限られます。
ルジャンドルの楕円積分計算であると、積分の範囲に制限はないので、これの逆変換です。
積分の範囲が±π/2の範囲を超えてしまっていて、微分できる計算になっていないようなので、ニュートン法の使用が難しく、適当な仮の値を与えて、積分を行い、値が小さかったら大きくし、大きかったら小さくするような計算方法をとったので計算に時間が掛かっています。
その代わり積分の計算に間違いがない限り、逆変換の値も正しい値を求めることが出来ます。
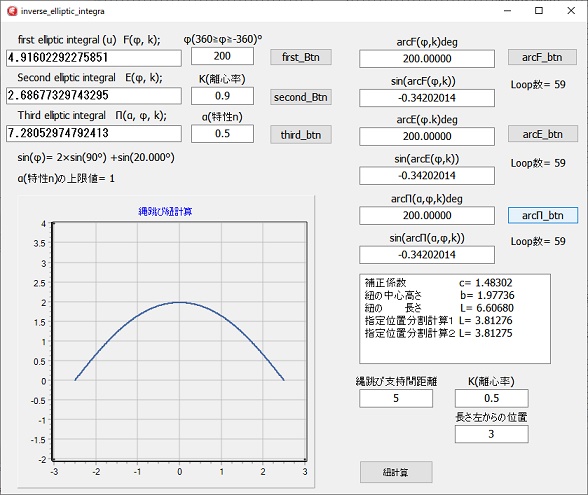最初に角度、離心率、第三種楕円積分の場合は、特性値も入力し、積分計算を行います。
計算を行うと、一番左側の枠に積分値が表示されます。
一番右側のarc計算ボタンをクリックすると、逆計算が行われ右側の表示枠にその結果が表示されます。
一番左の枠に適当な値をいれて、arc計算ボタンをクリックすると、指定された、離心率、特性値を利用して逆計算が行われます。
一番左の枠に値を入れる場合、値の大きさの制限はしていないので、逆計算した結果が３６０°以上になる場合もあります。
ループ数の表示は、逆計算のため、積分計算が実行された回数です。
ニュートン法が使用できれば数ループで収束するのですが、使用出来ないため、ループ数が多くなっています。
第一種楕円積分の逆変換は、ヤコビの楕円関数SNなので、SNを使用した、縄跳び紐の追加してみました。
SNの計算は、計算速度を早くするため、am(Φ)による計算にしました。
縄跳び紐の支持距離、離心率、左端からの距離を入力して紐決算ボタンをクリックすると、縄跳び紐のグラフと、紐の中心高さ、長さが表示されます。
左端からの距離による紐の長さの計算は、単純に計算できないので、分割積分計算が行われます。
プログラム
//-----------------------------------------------------
// 第一種第二種第三種楕円積分のプログラム
//-----------------------------------------------------
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls, VclTee.TeeGDIPlus,
VCLTee.TeEngine, VCLTee.Series, VCLTee.TeeProcs, VCLTee.Chart;
type
TForm1 = class(TForm)
Edit1: TEdit;
Label1: TLabel;
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
LabeledEdit3: TLabeledEdit;
third_btn: TButton;
Edit3: TEdit;
Label4: TLabel;
Edit5: TEdit;
Label5: TLabel;
Label6: TLabel;
first_Btn: TButton;
second_Btn: TButton;
LabeledEdit4: TLabeledEdit;
jacobi_sn_btn: TButton;
LabeledEdit5: TLabeledEdit;
Label2: TLabel;
LabeledEdit6: TLabeledEdit;
LabeledEdit7: TLabeledEdit;
arcE_btn: TButton;
LabeledEdit8: TLabeledEdit;
LabeledEdit9: TLabeledEdit;
arc_pi_btn: TButton;
Label3: TLabel;
Label7: TLabel;
Label8: TLabel;
LabeledEdit10: TLabeledEdit;
LabeledEdit11: TLabeledEdit;
Memo1: TMemo;
nawaBtn: TButton;
Chart1: TChart;
Series1: TLineSeries;
Series2: TPointSeries;
LabeledEdit12: TLabeledEdit;
procedure third_btnClick(Sender: TObject);
procedure first_BtnClick(Sender: TObject);
procedure second_BtnClick(Sender: TObject);
procedure jacobi_sn_btnClick(Sender: TObject);
procedure arcE_btnClick(Sender: TObject);
procedure arc_pi_btnClick(Sender: TObject);
procedure nawaBtnClick(Sender: TObject);
private
{ Private 宣言 }
function RJ(x1, y1, z1, p1: double): double;
function RF(x1, y1, z1: double): double;
function datainput(var k, deg: double): boolean;
function calc_first_elliptic_integral(k, deg: double; var ALFRG : byte): double;
function calc_second_elliptic_integral(k, deg: double; var ALFRG : byte): double;
function calc_Third_elliptic_integral(a, k, deg: double; var ALFRG : byte): double;
function R_jacobi_sn(u, k: double): double;
function arcE(u, k: double): double;
function arc_pi(a, u, k: double): double;
function Jacobi_sn(u, k: double): double;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses Math;
// Carlson's Elliptic Integral RJ
function TForm1.RJ(x1, y1, z1, p1: double): double;
var
s, fa, rj, rk : double;
la, mu : double;
al, be : double;
r1, a1, b1 : double;
a2, b2, mv, s1 : double;
rc, r0 : double;
s12, s13, s14 : double;
s15, s16 : double;
x2, y2, z2 : double;
x3, y3, z3 : double;
s2, s3, p2, p3 : double;
s4, s5 : double;
x31, y31, z31, p31 : double;
s22, s23, s2s3 : double;
procedure rcab;
begin
rc := 1;
a1 := al;
b1 := be;
repeat
r1 := rc;
la := 2 * sqrt(a1 * b1) + b1;
a2 := (a1 + la) / 4;
b2 := (b1 + la) / 4;
mv := (a1 + 2 * b1) / 3;
s1 := (b1 - a1) / (3 * mv);
s12 := s1 * s1;
s13 := s12 * s1;
s14 := s13 * s1;
s15 := s14 * s1;
s16 := s15 * s1;
rc := (1 + 3 * s12 / 10 + s13 / 7 + 3 * s14 / 8 + 9 * s15 / 22 + 159 * s16 / 208) / sqrt(mv);
a1 := a2;
b1 := b2;
until r1 = rc;
end;
function ss: double;
begin
x31 := x31 * x3;
y31 := y31 * y3;
z31 := z31 * z3;
p31 := p31 * p3;
result := (x31 + y31 + z31 + p31);
end;
begin
s := 0;
fa := 3;
rj := 0;
repeat
r0 := rj;
la := sqrt(x1 * y1) + sqrt(x1 * z1) + sqrt(y1 * z1);
mu := (x1 + y1 + z1 + 2 * p1) / 5;
x2 := (x1 + la) / 4;
y2 := (y1 + la) / 4;
z2 := (z1 + la) / 4;
p2 := (p1 + la) / 4;
x3 := 1 - x1 / mu;
y3 := 1 - y1 / mu;
z3 := 1 - z1 / mu;
p3 := 1 - p1 / mu;
x31 := x3;
y31 := y3;
z31 := z3;
p31 := 2 * p3;
s2 := ss / 4;
s3 := ss / 6;
s4 := ss / 8;
s5 := ss / 10;
al := (sqrt(x1) + sqrt(y1) + sqrt(z1)) * p1 + sqrt(x1 * y1 * z1);
al := al * al;
be := p1 * (p1 + la) * (p1 + la);
rcab;
s22 := 3 * s2 * s2 / 22;
s23 := s2 * s2 * s2 / 10;
s2s3 := s2 * s3 * 3 / 13;
s := s + fa * rc;
rk := 1 + 3 * s2 / 7 + s3 / 3 + s22 + s2s3 + 3 * s4 / 11 + 3 * s5 / 13 - s23;
fa := fa / 4;
mu := sqrt(1 / (mu * mu * mu));
rj := s + fa / 4 * (rk + 3 * s3 * s3 / 10 + 3 * s2 * s4 / 5) * mu;
x1 := x2;
y1 := y2;
z1 := z2;
p1 := p2;
until rj = r0;
result := rj;
end;
// Carlson's Elliptic Integral RF
function TForm1.RF(x1, y1, z1: double): double;
var
la, mu : double;
x2, y2, z2 : double;
x3, y3, z3 : double;
s2, s3 : double;
r0, rf : double;
s22, s23, s2s3, s32 : double;
begin
rf := 0;
repeat
r0 := rf;
la := sqrt(x1 * Y1) + sqrt(x1 * z1) + sqrt(y1 * z1);
mu := (x1 + y1 + z1) / 3;
x2 := (x1 + la) / 4;
y2 := (y1 + la) / 4;
z2 := (z1 + la) / 4;
x3 := 1 - x2 / mu;
y3 := 1 - y2 / mu;
z3 := 1 - z2 / mu;
s2 := (x3 * x3 + y3 * y3 + z3 * z3) / 4;
s3 := (x3 * x3 * x3 + y3 * y3 * y3 + z3 * z3 * z3) / 6;
s22 := s2 * s2 / 6;
s23 := 5 * s2 * s2 * s2 / 26;
s32 := 3 * s3 * s3 / 26;
s2s3 := s2 * s3 * 3 / 11;
rf := (1 + s2 / 5 + s3 / 7 + s22 + s2s3 + s23 + s32) / sqrt(mu);
x1 := x2;
y1 := y2;
z1 := z2;
until rf = r0;
result := rf;
end;
// 入力処理
function TForm1.datainput(var k, deg: double): boolean;
var
ch, J : integer;
eqd : double;
absdeg : double;
degmax, kmax: double;
begin
result := False;
val(LabeledEdit2.Text, deg, ch);
if ch <> 0 then begin
application.MessageBox('φ(deg)の値に間違いがあります。','φ(deg)',0);
exit;
end;
// 計算上角度の上限下限はありませんがが一応+-360°で限定
if abs(deg) > 360 then begin
application.MessageBox('360≧φ(deg)≧-360の値が範囲外です。','φ(deg)',0);
exit;
end;
val(LabeledEdit3.Text, k, ch);
if ch <> 0 then begin
application.MessageBox('k(離心率)の値に間違いがあります。','k(離心率)',0);
exit;
end;
if (k > 1) or (k < -1) then begin
degmax := arcsin(sqrt(1 / (k * k))) / pi * 180;
kmax := sin(deg / 180 * pi);
kmax := sqrt(1 / (kmax * kmax));
if deg > degmax then begin
application.MessageBox(pchar('角度の最大値は' + floatTostr(degmax) + #13#10
+ '又は離心率の最大値は' + floatTostr(kmax) + 'です。'),'k(離心率)',0);
// exit;
end;
end;
absdeg := abs(deg);
J := trunc(absdeg / 90);
if j mod 2 <> 0 then // 第２,第４象限の積分角度
eqd := (J + 1) * 90 - absdeg
else // 第1,第3象限の積分角度
eqd := absdeg - (90 * J);
if j mod 2 <> 0 then // 第２,第４象限の積分量
Label2.Caption := 'sin(φ)= ' + intTostr(J + 1) + '×sin(90°) -' +
'sin(' + floatTostrF(eqd, fffixed, 5, 3) + '°)'
else // 第1,第3象限の積分量
Label2.Caption := 'sin(φ)= ' + intTostr(J) + '×sin(90°) +' +
'sin(' + floatTostrF(eqd, ffFixed, 5, 3) + '°)';
result := true;
end;
// 第一種楕円積分 ルーチン
function TForm1.calc_first_elliptic_integral(k, deg: double; var ALFRG : byte): double;
var
J : integer;
s, s2 : double;
c2 : double;
rf0 : double;
k2 : double;
q, eq, eqd : double;
fqk, fek : double;
fqk90 : double;
qb : double;
begin
ALFRG := 0;
// fqk := 0;
qb := deg / 180 * pi; // rad単位
deg := abs(deg);
q := abs(qb);
J := trunc(deg / 90); // 90°分割数
if j > 0 then begin // 90°以上だったら
s2 := 1; // sin^2(90°)
end
else begin // 90°以下なら
s := sin(q); // sin(φ)
s2 := s * s; // sin~2(φ)
end;
if j mod 2 <> 0 then // 第２,第４象限の積分角度
eqd := (J + 1) * 90 - deg
else // 第1,第3象限の積分角度
eqd := deg - (90 * J);
eq := eqd / 180 * pi;
k2 := k * k; // k^2
if ((1 - k2 * s2) <= 0) then begin // 1-K^2*sin^2(φ) = 0 K=1 φ=π/2 なら
fqk := MAXDouble;
ALFRG := 1;
end
else begin // 1-K^2*sin^2(φ) > 0 なら
fqk90 := 0;
if J > 0 then begin // 90°以上だったら
rf0 := RF(0, 1 - k2, 1); // 90°のRF計算
fqk90 := rf0; // rf0 * sin90°= rf0 * 1 = F(90°,K)
end;
c2 := cos(eq) * cos(eq); // cos^2(φ')
s := sin(eq); // sin(φ')
s2 := s * s; // sin^2(φ')
rf0 := RF(c2, 1 - k2 * s2, 1);
fek := s * rf0; // F(φ',K) = rf0 * sin(φ')
if j mod 2 <> 0 then // 第２,第４象限の積分値
fqk := (j + 1) * fqk90 - fek
else // 第1,第3象限の積分値
fqk := j * fqk90 + fek;
if qb < 0 then fqk := - fqk; // 積分範囲の符号で積分値の符号設定
end;
result := fqk;
end;
// 第一種楕円積分
procedure TForm1.first_BtnClick(Sender: TObject);
var
ALFRG : byte;
k, deg: double;
fqk : double;
begin
if not datainput(k, deg) then exit;
first_Btn.Enabled := false;
fqk := calc_first_elliptic_integral(k, deg, ALFRG);
case ALFRG of
0: Edit5.Text := floatTostr(fqk);
1: Edit5.Text := '∞';
end;
first_Btn.Enabled := true;
end;
// 第二種楕円積分 ルーチン
function TForm1.calc_second_elliptic_integral(k, deg: double; var ALFRG : byte): double;
label
NO2;
var
J : integer;
s, s2, s3 : double;
c2 : double;
rf0 : double;
k2 : double;
eq, eqd : double;
eqk90 : double;
rd0 : double;
eqk, eek : double;
qb : double;
begin
ALFRG := 0;
qb := deg;
deg := abs(deg);
J := trunc(deg / 90);
if j mod 2 <> 0 then // 第２,第４象限の積分角度
eqd := (J + 1) * 90 - deg
else // 第1,第3象限の積分角度
eqd := deg - (90 * J);
eq := eqd / 180 * pi;
k2 := k * k; // k^2
eqk90 := 0;
if J > 0 then begin // 積分範囲90度より大きかったら
if (deg = 90 * J) and (k2 = 1) then begin
eqk := J;
goto NO2;
end
else
if k2 > 1 then begin
eqk90 := 1;
ALFRG := 1;
end
else begin // 90°の積分値計算
if k2 = 1 then eqk90 := 1
else begin
rf0 := RF(0, 1 - k2, 1);
rd0 := RJ(0, 1 - k2, 1, 1);
eqk90 := rf0 - k2 / 3 * rd0; // rf0 － k^2 / 3 * RD
end;
end;
end;
s := sin(eq);
s2 := s * s;
if (eqd < 90) or (k2 * s2 < 1) then begin
// if (eqd < 90) or (abs(K) < 1) then begin
if k2 * s2 < 1 Then begin
// if abs(K) < 1 Then begin
c2 := cos(eq) * cos(eq);
s3 := s2 * s;
rf0 := RF(c2, 1 - k2 * s2, 1);
rd0 := RJ(c2, 1 - k2 * s2, 1, 1);
eek := s * rf0 - k2 / 3 * s3 * rd0;
end
else begin
eek := 1;
ALFRG := 1;
end;
end
else begin
eek := 1;
ALFRG := 1;
end;
if j mod 2 <> 0 then begin // 第２,第４象限の積分値
eqk := (J + 1) * eqk90 - eek;
end
else begin // 第1,第3象限の積分値
eqk := J * eqk90 + eek;
end;
NO2:
if qb < 0 then eqk := -eqk;
result := eqk;
end;
// 第二種楕円積分
procedure TForm1.second_BtnClick(Sender: TObject);
var
k, deg : double;
eqk : double;
ALFRG : byte;
begin
if not datainput(k, deg) then exit;
second_Btn.Enabled := false;
eqk := calc_second_elliptic_integral(k, deg, ALFRG);
case ALFRG of
0: Edit3.Text := floatTostr(eqk); // 第二種
1: Edit3.Text := 'k(離心率)の値が大きすぎます。'
end;
second_Btn.Enabled := true;
end;
// 第三種楕円積分 ルーチン
function TForm1.calc_Third_elliptic_integral(a, k, deg : double; var ALFRG : byte): double;
var
J : integer;
s, s2, s3 : double;
c2 : double;
rf0, rj0 : double;
k2 : double;
afk, aek : double;
afk90, qb : double;
q, eq, eqd : double;
fek : double;
begin
ALFRG := 0;
// afk := 0;
qb := deg / 180 * pi;
q := abs(qb);
deg := abs(deg);
J := trunc(deg / 90);
if j > 0 then begin // 90°以上だったら
s2 := 1; // sin^2(90°)
end
else begin // 90°以下なら
s := sin(q); // sin(φ)
s2 := s * s; // sin~2(φ)
end;
if j mod 2 <> 0 then // 第２,第４象限の積分角度
eqd := (J + 1) * 90 - deg
else // 第1,第3象限の積分角度
eqd := deg - (90 * J);
eq := eqd / 180 * pi;
k2 := k * k; // k^2
if ((1 - k2 * s2) <= 0) then begin // 1-K^2*sin^2(φ) = 0 K=1 φ=π/2 なら
ALFRG := 1;
afk := MaxDouble;
if (1 - a * s2) < 0 then ALFRG := 2
else ALFRG := 1;
end
else begin // 1-K^2*sin^2(φ) > 0 なら
if (1 - a * s2) <= 0 then begin // aの値が大きすぎたら
afk := MaxDouble;
if (1 - a * s2) = 0 then ALFRG := 1 // 1-a^2*sin^2(φ) がゼロのフラグセット
else ALFRG := 2; // 1-a^2*sin^2(φ) がマイナスフラグセット
end
else begin
afk90 := 0;
if J > 0 then begin // 90°以上だったら
rf0 := RF(0, 1 - k2, 1); // 90°のRF計算
rj0 := RJ(0, 1 - k2, 1, 1 - a * 1); // 90°のRj計算
afk90 := rf0 + a / 3 * rj0; // Π(a, 90°,K)
end;
c2 := cos(eq) * cos(eq); // cos^2(φ')
s := sin(eq); // sin(φ')
s2 := s * s; // sin^2(φ')
s3 := s2 * s; // sin^2(φ')
rf0 := RF(c2, 1 - k2 * s2, 1);
rj0 := RJ(c2, 1 - k2 * s2, 1, 1 - a * s2);
fek := s * rf0; // F(φ',K) = rf0 * sin(φ')
aek := fek + a / 3 * s3 * rj0; // Π(a,φ',K)
if j mod 2 <> 0 then begin // 第２,第４象限の積分値
afk := (j + 1) * afk90 - aek;
end
else begin // 第1,第3象限の積分値
afk := j * afk90 + aek;
end;
if qb < 0 then begin // 積分範囲の符号で積分値の符号設定
afk := - afk;
end;
end;
end;
result := afk;
end;
// 第三種楕円積分
procedure TForm1.third_btnClick(Sender: TObject);
var
ALFRG : byte;
a, k, deg : double;
afk, alfa : double;
ch : integer;
absdeg : double;
begin
if not datainput(k, deg) then exit;
val(LabeledEdit1.Text, a, ch);
if ch <> 0 then begin
application.MessageBox('a(特性)の値に間違いがあります。','a(特性)',0);
exit;
end;
third_btn.Enabled := false;
absdeg := abs(deg);
if absdeg > 90 then alfa := 1
else alfa := sin(absdeg / 180 * pi);
if alfa > 0 then begin
alfa := 1 / alfa / alfa;
label6.Caption := 'α(特性n)の上限値= ' + floatTostr(alfa);
end
else
label6.Caption := 'α(特性n)の上限値= ∞';
afk := calc_Third_elliptic_integral(a, k, deg, ALFRG);
case ALFRG of
0 : Edit1.Text := floatTostr(afk); // 第三種
1 : Edit1.Text := '∞'; // 演算誤差により発生率低い
2 : Edit1.Text := 'a(特性n)の値が大きすぎ'
end;
third_btn.Enabled := true;
end;
// 第一種楕円積分逆変換ルーチン
// 此処ではdeg単位で計算します
// k=1 で90度に近い場合非常に大きな値となり精度Doubleでは扱える値を超え
// 収束判定が出来ない為別途ルーチンを分けて計算します。
function TForm1.R_jacobi_sn(u, k: double): double;
const
Keps = 1E-12;
KN = 1000;
var
ALFRG : byte;
deg : double;
ud, ddeg : double;
i : integer;
absu : double;
begin
absu := abs(u); // uの絶対値
ddeg := 45; // 初期補正角度設定
if abs(k) = 1 then begin // 離心率kが１の時 90°だと∞になるので別途計算
deg:= 90 - sqrt(Keps); // 90°に近い値セット
ud := calc_first_elliptic_integral(k, deg, ALFRG); // 第一種楕円積分
if ud < absu then begin // 90°に近い値より大きかったら
if u < 0 then deg := -deg;
result := deg; // 90°に近い値を戻り値に
Label3.Caption := 'Loop数= 0';
exit;
end;
deg := 0; // 初期角度セット
for i := 0 to KN do begin
ud := calc_first_elliptic_integral(k, deg, ALFRG); // 第一種楕円積分
if abs(ud - absu) < Keps then break; // 積分値と指定値の差が誤差設定値より小さくなったら終了
if ud < absu then begin // 積分値が指定値より小さかったら
if deg + ddeg >= 90 then begin // 補正値を加算した場合90°を超える場合
ddeg := 90 - deg - sqrt(Keps); // 90°を超えない範囲に補正値を修正
end;
end
else begin // 指定値より大きかったら
deg := deg - ddeg; // 角度減算
ddeg := ddeg / 2; // 補正値２分の１
end;
deg := deg + ddeg; // 角度補正値加算
if ddeg < Keps then break; // 角度補正値が収束判定値より小さくなったら終了
end;
end
else begin // 離心率が１以下の場合
deg := 45; // 初期値設定
for i := 0 to KN do begin
ud := calc_first_elliptic_integral(k, deg, ALFRG); // 第一種楕円積分
if abs(ud - absu) < Keps then break; // 積分値と指定値の差が誤差設定値より小さくなったら終了
if ud > absu then begin // 積分値が指定値より大きかったら
deg := deg - ddeg; // 補正値減算
ddeg := ddeg / 2; // 補正値２分の１に
end;
deg := deg + ddeg; // 補正値加算
if ddeg < Keps then break; // 角度補正値が収束判定値より小さくなったら終了
end;
end;
Label3.Caption := 'Loop数= ' + intTostr(i);
if u < 0 then deg := -deg;
result := deg;
end;
// 第一種楕円積分逆変換
// jacobi_snの場合は値は sn u = -1<= u' <=1
// uの値は -pi/2 <= u <= pi/2
// 離心率は -1<= k <=1 となります。
// 第一種楕円積分の逆関数という事で制限を外しました。
procedure TForm1.jacobi_sn_btnClick(Sender: TObject);
var
u, k, sn : double;
ch: integer;
snsin : double;
begin
val(Edit5.Text, u, ch);
if ch <> 0 then begin
application.MessageBox('first elliptic integral (u)に間違いがあります。','注意',0);
exit;
end;
// if abs(u) > pi/ 2 then begin
// application.MessageBox('uの最大値は±pi/2です。','注意',0);
// exit;
// end;
val(LabeledEdit3.Text, k, ch);
if ch <> 0 then begin
application.MessageBox('k(離心率)に間違いがあります。','注意',0);
exit;
end;
// if abs(k) > 1 then begin
// application.MessageBox('k(離心率)の最大値は±１です。','注意',0);
// exit;
// end;
sn := R_jacobi_sn(u, k);
Labelededit4.Text := floatTostrF(sn, ffFixed, 10, 5);
snsin := sin(sn / 180 * pi);
Labelededit5.Text := floatTostrF(snsin, ffFixed, 10, 8);
end;
// 第二種楕円積分逆変換ルーチン
function TForm1.arcE(u, k: double): double;
const
KN = 1000;
Keps = 1E-12;
var
deg : double;
ud, ddeg : double;
i : integer;
ALFRG : byte;
begin
ddeg := 45; // 角度補正値
deg := ddeg; // 初期値
for i := 0 to KN do begin
ud := calc_second_elliptic_integral(k, deg, ALFRG); // 第二種楕円積分
if abs(ud - abs(u)) < Keps then break; // 積分値と指定値の差が誤差設定値より小さくなったら終了
if ud > abs(u) then begin // 指定値より大きかったら
deg := deg - ddeg; // 補正値減算
ddeg := ddeg / 2; // 補正値二分の一
end;
deg := deg + ddeg; // 補正値加算
if ddeg < Keps then break; // 角度補正値が収束判定値より小さくなったら終了
end;
if u < 0 then deg := -deg;
Label7.Caption := 'Loop数= ' + intTostr(i);
result := deg;
end;
// 第二種楕円積分逆変換
procedure TForm1.arcE_btnClick(Sender: TObject);
var
u, k, en : double;
ch: integer;
ensin : double;
begin
val(Edit3.Text, u, ch);
if ch <> 0 then begin
application.MessageBox('second elliptic integralに間違いがあります。','注意',0);
exit;
end;
val(LabeledEdit3.Text, k, ch);
if ch <> 0 then begin
application.MessageBox('k(離心率)に間違いがあります。','注意',0);
exit;
end;
en := arcE(u, k);
Labelededit6.Text := floatTostrF(en, ffFixed, 10, 5);
ensin := sin(en / 180 * pi);
Labelededit7.Text := floatTostrF(ensin, ffFixed, 10, 8);
end;
// 第三種楕円積分逆変換ルーチン
function TForm1.arc_pi(a, u, k: double): double;
const
Keps = 1E-12;
KN = 1000;
var
ALFRG : byte;
deg : double;
ud, ddeg : double;
eps : double;
i : integer;
absu : double;
begin
ALFRG := 0;
eps := Keps;
ddeg := 45;
deg := ddeg;
absu := abs(u);
if abs(k) = 1 then begin // 離心率kが１の時 90°だと∞になるので別途計算
deg:= 90 - sqrt(Keps); // 90°に近い値セット
ud := calc_third_elliptic_integral(a, k, deg, ALFRG); // 第三種楕円積分
if ud < absu then begin // 90°に近い値より大きかったら
if u < 0 then deg := -deg;
result := deg; // 90°に近い値を戻り値に
Label8.Caption := 'Loop数= 0';
exit;
end;
deg := 0; // 初期角度セット
for i := 0 to KN do begin
ud := calc_third_elliptic_integral(a, k, deg, ALFRG); // 第三種楕円積分
if abs(ud - absu) < Keps then break; // 積分値と指定値の差が誤差設定値より小さくなったら終了
if ud < absu then begin // 積分値が指定値より小さかったら
if deg + ddeg >= 90 then begin // 補正値を加算した場合90°を超える場合
ddeg := 90 - deg - sqrt(Keps); // 90°を超えない範囲に補正値を修正
end;
end
else begin // 指定値より大きかったら
deg := deg - ddeg; // 角度減算
ddeg := ddeg / 2; // 補正値２分の１
end;
deg := deg + ddeg; // 角度補正値加算
if ddeg < Keps then break; // 角度補正値が収束判定値より小さくなったら終了
end;
Label8.Caption := 'Loop数= ' + intTostr(i);
result := deg;
exit;
end; // 離心率kが１以下の計算
for i := 0 to KN do begin
ud := calc_Third_elliptic_integral(a, k, deg, ALFRG); // 第三種楕円積分
if abs(ud - absu) < eps then begin // 積分値と指定値の差が誤差設定値より小さくなったら終了
if u < 0 then deg := -deg;
break;
end;
if ud > absu then begin // 積分値が指定値より大きかったら
deg := deg - ddeg; // 角度減算
ddeg := ddeg / 2; // 補正値２分の１
end;
deg := deg + ddeg; // 角度補正値加算
if ddeg < Keps then break; // 角度補正値が収束判定値より小さくなったら終了
end;
Label8.Caption := 'Loop数= ' + intTostr(i);
result := deg;
end;
// 第三種楕円積分逆変換
procedure TForm1.arc_pi_btnClick(Sender: TObject);
var
a : double;
u, k, pn : double;
ch: integer;
pnsin : double;
begin
val(LabeledEdit1.Text, a, ch);
if ch <> 0 then begin
application.MessageBox('a(特性)の値に間違いがあります。','a(特性)',0);
exit;
end;
val(Edit1.Text, u, ch);
if ch <> 0 then begin
application.MessageBox('Third elliptic integralに間違いがあります。','注意',0);
exit;
end;
val(LabeledEdit3.Text, k, ch);
if ch <> 0 then begin
application.MessageBox('k(離心率)に間違いがあります。','注意',0);
exit;
end;
pn := arc_pi(a, u, k);
Labelededit8.Text := floatTostrF(pn, ffFixed, 10, 5);
pnsin := sin(pn / 180 * pi);
Labelededit9.Text := floatTostrF(pnsin, ffFixed, 10, 8);
end;
// Jacobi関数 Jacobi sn(u, k)
function TForm1.Jacobi_sn(u, k: double): double;
const
N = 30;
EPSILON = 1E-15;
var
a: array[0..N] of Extended;
g: array[0..N] of Extended;
c: array[0..N] of Extended;
two_n : Extended;
phi : Extended;
half : Extended;
i, j : integer;
begin
half := 1 / 2;
if k = 0 then begin
result := sin(u);
exit;
end;
if k = 1 then begin
result := sin(2 * arctan(exp(u)) - pi / 2);
exit;
end;
a[0] := 1;
g[0] := sqrt(1 - k * k);
c[0] := k;
two_n := 1;
for i := 0 to N do begin
if abs(a[i] - g[i]) < a[i] * EPSILON then break;
two_n := two_n + two_n;
a[i + 1] := half * (a[i] + g[i]);
g[i + 1] := sqrt(a[i] * g[i]);
c[i + 1] := half * (a[i] - g[i]);
end;
phi := two_n * a[i] * u;
for j := i downto 1 do
phi := half * (phi + arcsin(c[j] * sin(phi) / a[j]));
result := sin(phi);
end;
// 縄跳びの縄弛み計算
procedure TForm1.nawaBtnClick(Sender: TObject);
const
kN = 400;
var
ALFRG : byte;
k, deg : double;
ch : integer;
a, a2 : double;
fkd, b, u : double;
c, L : double;
Ek : double;
i : integer;
x, y, dx : double;
snuk : double;
ty, by : double;
lx, rx : double;
def, ddf : double;
siguma : double;
Lp : double;
LLp : double;
dx2 : double;
yb : double;
begin
val(Labelededit10.Text, a2, ch);
if ch <> 0 then begin
application.MessageBox('縄跳び紐支持間に間違いがあります。','注意',0);
exit;
end;
val(LabeledEdit11.Text, k, ch);
if ch <> 0 then begin
application.MessageBox('縄跳び紐離心率Ｋに間違いがあります。','注意',0);
exit;
end;
if abs(k) >= 1 then begin
application.MessageBox('k(離心率)は最大値＜abs(±１)です。','注意',0);
exit;
end;
val(LabeledEdit12.Text, Lp, ch);
if ch <> 0 then begin
application.MessageBox('左からの位置に間違いがあります。','注意',0);
exit;
end;
memo1.Clear;
ALFRG := 0;
deg := 180; //
fkd := calc_first_elliptic_integral(k, deg, ALFRG); // 180°第一種楕円積分
if fkd = 0 then begin
memo1.Lines.Add('支持間の距離係数 第一種楕円積分の');
memo1.Lines.Add('積分値の値がゼロになります。');
memo1.Lines.Add('Kの値を１以下にして下さい。');
exit;
end;
// 各種計算
a := a2 / 2;
c := a2 / fkd; // 積分値に対する補正係数
b := 2 * k / (1 - k * k) * c; // 最大値 90°の位置
deg := 180;
Ek := calc_second_elliptic_integral(k, deg, ALFRG); // 第二種積分(180°)
L := 2 * c * Ek / (1 - k * k) - a2; // 弧の長さ計算
memo1.Lines.Add('補正係数 c= ' + floatTostrF(c, ffFixed, 10, 5));
memo1.Lines.Add('紐の中心高さ b= ' + floatTostrF(b, ffFixed, 10, 5));
memo1.Lines.Add('紐の 長さ L= ' + floatTostrF(L, ffFixed, 10, 5));
Series1.Clear;
Series2.Clear;
// グラフスケール設定
if a2 > b then begin
ddf := a2 / 10;
def := (a2 - b) / 2;
ty := b + def + ddf;
by := 0 - def - ddf;
rx := a + ddf;
lx := -a - ddf;
end
else begin
ddf := b / 10;
def := (b - a2) / 2;
ty := b + ddf;
by := 0 - ddf;
rx := a + def + ddf;
lx := -a - def - ddf;
end;
// グラフのスケール設定値セット
Series2.AddXY(lx, ty);
Series2.AddXY(lx, by);
Series2.AddXY(rx, by);
application.ProcessMessages;
// グラフ作図と分割積分
dx := a2 / KN; // ΔX
// 0～KN 計算作図 距離積分
Series1.AddXY(-a, 0); // グラフに追加
for i := 1 to KN do begin
x := i * dx; // x位置
u := x / c; // F(α,k)=u
// jacobi_sn ヤコビの楕円関数
snuk := jacobi_sn(u, k);
y := snuk * b; // x位置のyの値
Series1.AddXY(x - a, y); // グラフに追加
end;
// グラフ作図と分割積分
dx := Lp / KN; // ΔX
// 0～KN 計算作図 距離積分
yb := 0;
dx2 := dx * dx; // dx^2
siguma := 0; // 合計値クリア
for i := 1 to KN do begin // 指定位置長さ積分
x := i * dx; // x位置
u := x / c; // F(α,k)=u
// jacobi_sn ヤコビの楕円関数
snuk := jacobi_sn(u, k);
y := snuk * b; // x位置のyの値
ty := (y - yb); // Δy
siguma := siguma + sqrt(dx2 + ty * ty); // 長さの合計
yb := y;
end;
memo1.Lines.Add('指定位置分割計算１ L= ' + floatTostrF(siguma, ffFixed, 10, 5));
application.ProcessMessages;
// 長さ分割積分
dx := Lp / (KN div 4); // ΔX
dx2 := dx / 2; // ΔX / 2
siguma := 0; // 合計値クリア
for i := 0 to (KN div 4) - 1 do begin
x := i * dx + dx2; // +dx2 は x位置中間位置で計算の為
u := x / c; // F(α,k)=u
// jacobi_sn
snuk := jacobi_sn(u, k); // jacobi_sn(u, k)が角度の為sin(α°)計算
y := (1 - k * k * snuk * snuk); // dn^2(u) = 1-K^2*sn^2(u)
siguma := siguma + y; // 積分 合計値
end;
LLP := 2 / (1- k * k) * siguma * dx - Lp; // 距離
memo1.Lines.Add('指定位置分割計算２ L= ' + floatTostrF(LLP, ffFixed, 10, 5));
end;
end.
inverse_elliptic_integra.zip
各種プログラム計算例に戻る