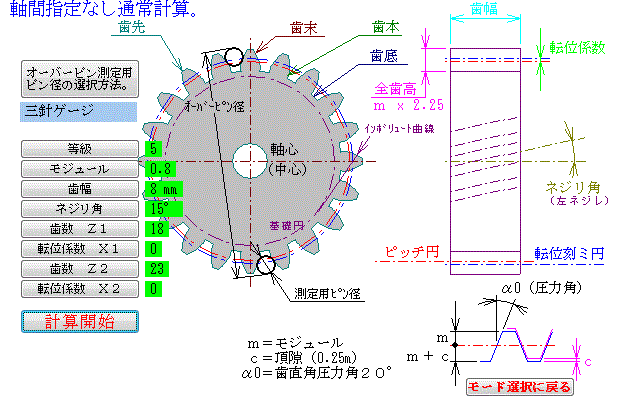
ハスバ歯車の計算　ネジリ角をゼロにとれば、平歯車の計算も出来ます。

　上図は、ギヤのデーター入力画面です、詳しい内容は、専門書を参照して下さい。
小原歯車のホームページでも、資料を公開しているので参照をすると良いでしょう。
インターネットで"小原歯車"の検索を実行すれば直ぐに見つかります、初心者用から、設計者用まで、可なり詳しく紹介しています。
本プログラムは、普通の状態でギヤを設計する場合は必要ありません、軸間が決まっていて、その中に決められたギヤ比でギヤを入れる必要がある場合に使用します。
手計算で何度も繰り返し計算をすれば、答えを出すことが可能ですが、それでは作業が大変なので、プログラムで近似値を求める為のプログラムです。
　転位係数は容易に導き出すことが出来ますが、ネジリ角の解を導き出すことは出来ません。
ネジリ角は、少しずつ角度を変え指定の軸間距離を越えたら、元へ戻し角度を変える値を小さくして、又、少しずつ角度を変える事を繰り返し、角度を変える値が　1E-9　より小さくなったら計算終了としています。
計算結果としては軸間距離精度、１／１０００㎜程度の精度は出せます。
本プログラムでは、計算の終了をネジリ角で判定していますが、ネジリ角で判定するのではなく、指定された軸間距離と計算したした軸間距離の差で判定したほうが良いでしょう。
又、誤差が気になるようであれば、桁落ちするところを判定基準として、計算するようにプログラムを修正しれば良いでしょう。
ネジリ角の解析解が求められない理由は、ネジリ角の計算に逆インボーリュート関数が必要で、これに解析解が無いためです。

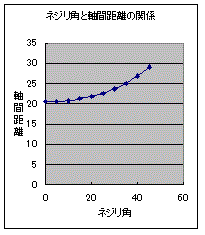
　上図左は、ネジリ角による軸間の変化のグラフの一例です。
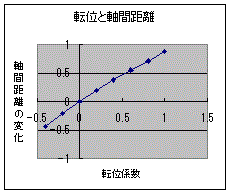
右の図は、転位した場合ですが、転位の量に直線的に軸間が変化するわけではないので注意が必要です。
プログラムの中に転位した場合の問題を確認する為の、切り下げ、歯の先端の状態を確認するためのグラフィックルーチンを組み込んであります。
あまりねじり角を大きくすると、ネジリ角による軸と平行方向へのスラスト荷重が増加し、軸受けの負担が増加します。
回転の伝達は滑らかになり、計算上の伝達効率は僅かに低下しますが、実際の伝達で十分に潤滑されている場合は全く問題ないようです。
ネジリの無い平歯車の場合、歯のかみ合い枚数が回転方向の角度によって変化する為、騒音や振動の元なります。
現実には、荷重によって、歯面は歪が、歯には撓みが発生するため理論通りには噛み合いません。
荷重の大きさ、材質、幅、歯車の大きさ、軸や、その周りの構成によって、歯車の歯面の修正が必要となりますが、本プログラムにはその様な事は盛り込まれていません、単に理論値の計算のみです。

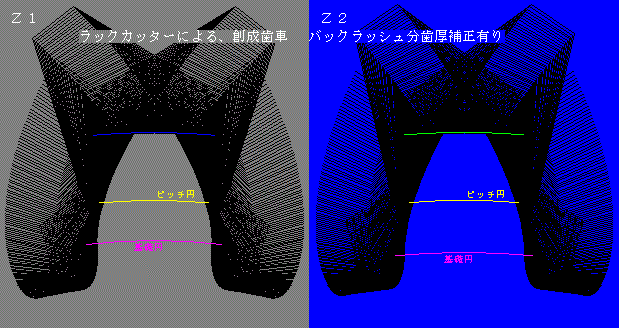
　プログラムの中で、ラックカッターにより歯車を創成した場合をグラフィックで表示出来る様になっています、プラス転位した場合の歯の先端と、マイナス転位した場合の切り下げの状況を歯車を製作せずに確認する為です。

　本プログラム中で使用している逆インボリュートサブルーチン、ニュートン法のサブルーチンです。
逆インボリュートの仮の値として、求める逆インボリュートの値より大きい値をDISASに与えています、もし、これが小さいと計算は収束せず答えが出ません。
収束の判定はCHECK＝　1E-9　となっていますが　　1E-7　程度ても全く問題ありません。
ｉｆ　文は９０°になってしまうと、ｔａｎ（θ）の計算時オーバーフローエラーになり計算が中断する為、それを防止するためです。
Ｌｏｏｐｓはrepeat文の中から抜け出すことが出来なくなったばあい強制的に抜け出す為のものです。
　ギヤのデーターとして問題ない値が入力されれば良いのですが、どの様な値が入力されるかは解りません。
その時に演算エラーとなると、最初からやり直す必要が出るのでその様な事が無い様にする為のものです。
通常であると答えは、二十回程度でループが終了します。
逆インボリュートの値は可なり正確で、逆インボリュート関数表と全く同じ答えに成るでしょう。
プログラム例として逆インボリュート関数があり、その中に計算精度　倍精度で桁落ちするまで計算した場合の計算例があるので、試してみると良いでしょう。

(注)　本プログラムで計算した全ての確認計算結果の確認が取れているわけではありません、もし、問題がある場所は修正して下さい。