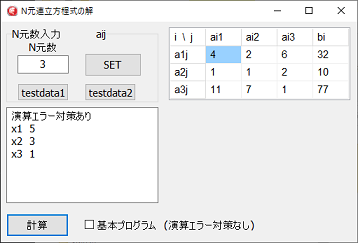
 次数を入力してセットボタンをクリックすれば、右側のグリッドボックスが次数の大きさに応じて変更されます。
次数を入力してセットボタンをクリックすれば、右側のグリッドボックスが次数の大きさに応じて変更されます。testdata1は4元、testdata2は3元での計算テスト用の値がセットされます。
プログラムには、単純に一行目からの前進消去で、ピボットの最大値の検索を行わない基本プログラムと、最大値の検索を行い、行の交換を行うルーチンが組み込まれており、チェックボックスで選択できるようになっています。
ガウスの消去法
改良版を一次方程式の解法8に追加しました。
ガウスの消去法については、近似式計算で使用しているのですが、N元一次方程式の解法として別途作成しました。
N元一次方程式解放
a11x1
+ a12x2
+ … + a1nxn
= b1
a21x1
+ a22x2
+ … + a2nxn
= b2
・
・
an1x1
+ an2x2
+ … + annxn
= bn
前進消去を行います。
例えば、一行目のa11と二行目のa21の値が1になるように一行目はa11、二行目はa21で除算を繰り返し全ての行のan1の値が全て1になるようにします。
an1がゼロの場合は、除算は出来ませんので其のままです。
次に、一行目を二行目以降から減算すると一行目を残し、an1の値がゼロになります、元々an1がゼロの場合は、其のままです。
更に二行目以降のan2が1になるようにして、二行目を三行め以降から減算すれば二行目を残して、三行目以降のan2がゼロになります。
an2が元々ゼロだった場合は其のままです。
これを繰り返せば、xn=b'nが最後に求まります。
x1
+ a'12x2
+ … + a'1nxn
= b'1
x2
+ … + a'2nxn
= b'2
・
・
xn
= b'n
後退代入を行います。
xn
= b'n を上の行に代入し xn-1
= b'n-1 を求め更に上の行に代入を繰り返すことで全ての 、X1~Xnの値を求める事が出来ます。
問題は、a の値にゼロが現れる場合で 例えば一行目のa11の値が、ゼロ或いはゼロに近い場合、計算が出来ないので、an1の値が一番大きい行と入れ替えを行い計算します。
二行目に計算が移り、二行目のa22がゼロに近いかゼロの場合は、二行目以降のan2の一番大きいの行と入れ替えて計算するように繰り返しながら計算します。
実際には、ann値に関係なく一番大きいannの値の行を検索しながら計算し、もし、annの値がゼロ或いはゼロに近い値しかなくなった場合は、解が存在しないことになります。
此処での説明は対角のannの値が1になりますが、計算方法によっては、1にならない場合もあります。
また、計算上1にする必要はないのに、計算の最後に1に設定しているのもあります。(行列式の辻褄合わせ)
対角のannが1にならない前進消去
前進消去の時、最初に二行目のa21/a11を一行目に乗算して、一行目から二行目を減算し、三行目の、a31/a11を一行目に乗算して一行目から三行目を減算n行目迄処理を繰り返します。
次に、三行目のa'32/a'22を二行目に乗算して三行目を減算、四行目のa'42/a'22を二行目に乗算してを四行目減算をn行目迄繰り返します。
n行まで処理が終了したら前進消去完了です。
対角の値が1にならないので、後退処理の時1になるように処理します。
a'11x1
+ a'12x2
+ … + a'1nxn
= b'1
a'22x2
+ … + a'2nxn
= b'2
・
・
a'nnxn
= b'n
無駄なようですが、ピボットの値がゼロに成るのを防止するルーチンの場合、処理が簡単になります。
インターネットでガウスの消去法を検索すれば、沢山見つかるので、参照してください。
 次数を入力してセットボタンをクリックすれば、右側のグリッドボックスが次数の大きさに応じて変更されます。
次数を入力してセットボタンをクリックすれば、右側のグリッドボックスが次数の大きさに応じて変更されます。
testdata1は4元、testdata2は3元での計算テスト用の値がセットされます。
プログラムには、単純に一行目からの前進消去で、ピボットの最大値の検索を行わない基本プログラムと、最大値の検索を行い、行の交換を行うルーチンが組み込まれており、チェックボックスで選択できるようになっています。
プログラム
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.Grids, Vcl.ExtCtrls,
Vcl.Buttons;
type
TForm1 = class(TForm)
Memo1: TMemo;
Button1: TButton;
StringGrid1: TStringGrid;
GroupBox1: TGroupBox;
LabeledEdit1: TLabeledEdit;
Button2: TButton;
CheckBox1: TCheckBox;
BitBtn1: TBitBtn;
BitBtn2: TBitBtn;
procedure Button1Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure Button2Click(Sender: TObject);
procedure BitBtn1Click(Sender: TObject);
procedure BitBtn2Click(Sender: TObject);
private
{ Private 宣言 }
procedure gauss_elimination; // ガウスの消去法
procedure gauss_elimination_basic;
procedure GridSet(Colin, Sin: integer); // グリッドサイズ変更
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
var
N : integer = 3; // 行列の大きさ初期値 検算用サイズ
a : array of array of double;
b : array of double;
cHeight, cWidth : integer; // フォームサイズ
// ガウスの消去法 基本
// 演算対策が無いので条件によってpivotにゼロが発生し演算エラーになります
// 配列は0 baseです
procedure TForm1.gauss_elimination_basic;
var
i, j, k : Integer;
pivot, p : double;
begin
// 前進消去
for j := 0 to N - 1 do begin
pivot := a[j, j]; // 対角値をpivotに代入
for k := j to N - 1 do
a[j, k] := a[j, k] / pivot; // pivotで行列を割りa[j,j]を1にします
b[j] := b[j] / pivot; // 定数ベクトルもpivotで割ります
for i := j + 1 to N - 1 do begin
p := a[i, j]; // j+1行以降j列の値
for k := j to N - 1 do
a[i, k] := a[i, k] - p * a[j, k]; // 係数行列のj+1行目からj行目の定数倍を引く
b[i] := b[i] - p * b[j]; // 定数ベクトルのj+1行目からj行目の定数倍を引く
end;
end;
// 後退代入
for i := N - 1 downto 0 do begin // 最終行から後退処理をします
for j := 0 to i - 1 do
b[j] := b[j] - a[j, i] * b[i]; // 代入処理をします
end;
// 解の表示
for i := 0 to N - 1 do
memo1.Lines.Append('x' + inttostr(i + 1) + ' ' + floatTostr(b[i]));
end;
{$DEFINE NNM2} // この条件シンボルで前進消去でa[k,k]の値が1にならない計算をします。
// 変更すれば 前進消去でa[k,k]の値が1になります。
// ガウスの消去法
// ピボット絶対値が大きい順に計算をします
// 配列は0 baseです
procedure TForm1.gauss_elimination;
var
i, j, k, p : integer;
pivotmax, s : double;
begin
// 前進消去(ピボット選択)
{$IFDEF NNM2}
for k := 0 to N - 2 do begin // 第kステップ
{$ELSE}
for k := 0 to N - 1 do begin // 第kステップ
{$ENDIF}
p := k; // k行目
pivotmax := abs(a[k][k]);
for i := k + 1 to N - 1 do begin // ピボット選択 一番大きい絶対値の選択
if abs(a[i][k]) > pivotmax then begin
p := i; // i行目
pivotmax := abs(a[i][k]);
end;
end;
// エラー処理:ピボットがあまりに小さい時はメッセージを表示して終了
if abs(pivotmax) < 1.0e-12 then begin
memo1.Lines.Append('ピボットの値が小さすぎます。');
exit;;
end;
if p <> k then begin // 第k行と第p行の入れ替え
for i := k to N - 1 do begin
// 係数行列 入れ替え
s := a[k][i];
a[k][i] := a[p][i];
a[p][i] := s;
end;
// 既知ベクトル 入れ替え
s := b[k];
b[k] := b[p];
b[p] := s;
end;
{$IFDEF NNM2}
{$ELSE}
pivotmax := a[k][k];
a[k][k] := 1; // a[k][k] / a[k][k] = 1 除算省略
for i := k + 1 to N - 1 do
a[k][i] := a[k][i] / pivotmax; // ピボットで除算してa[k][k]を1にします
b[k] := b[k] / pivotmax; // 既知ベクトルをピボットで除算
{$ENDIF}
// 前進消去
for i := k + 1 to N - 1 do begin // 第i行
{$IFDEF NNM2}
s := a[i][k] / a[k][k];
{$ELSE}
s := a[i][k];
{$ENDIF}
// 第k行を a[i][k] / a[k][k] 倍して、第i行から減算します
a[i][k] := 0.0; // 無くても可。
for j := k + 1 to N - 1 do
a[i][j] := a[i][j] - a[k][j] * s;
b[i] := b[i] - b[k] * s;
end;
end;
// 後退代入
for i := N - 1 downto 0 do begin // 最後の行から
for j := i + 1 to N - 1 do begin
b[i] := b[i] - a[i][j] * b[j];
{$IFDEF NNM2}
a[i][j] := 0.0; // 無くても可
{$ENDIF}
end;
{$IFDEF NNM2}
b[i] := b[i] / a[i][i];
a[i][i] := 1.0; // 無くても可
{$ENDIF}
end;
// 解の表示
for i := 0 to N - 1 do
memo1.Lines.Append('x' + inttostr(i + 1) + ' ' + floatTostr(b[i]));
end;
// グリッドサイズの変更 と フォームのサイズ設定
procedure TForm1.GridSet(Colin, Sin: integer); // グリッドサイズ変更
var // データー行の数は10迄
E, H, W : integer; // それ以上はスクロールする
begin
if (StringGrid1.ColCount = Colin) and (StringGrid1.RowCount = Sin) then exit;
StringGrid1.ColCount := Colin;
StringGrid1.RowCount := Sin;
if Sin <= 11 then // ストリンググリッドの大きさ設定
begin // 固定行を含め11行又はそれ以下の場合
H := (StringGrid1.DefaultRowHeight + 1) * Sin;
W := (StringGrid1.DefaultColWidth + 1) * Colin;
StringGrid1.ScrollBars := ssNone; // スクロールバーなし
end
else
begin // 固定行を含め11行より多い場合
H := (StringGrid1.DefaultRowHeight + 1) * (10 + 1);
W := (StringGrid1.DefaultColWidth + 1) * (11 + 1);
StringGrid1.ScrollBars := ssBoth; // スクロールバー表示
end;
StringGrid1.ClientWidth := W;
StringGrid1.ClientHeight := H;
for E := 1 to Sin - 1 do begin
StringGrid1.Cells[0, E] := 'a' + intTostr(E) + 'j';
StringGrid1.Cells[E, 0] := 'ai' + intTostr(E);
end;
StringGrid1.Cells[0, 0] := 'i \ j';
StringGrid1.Cells[sin, 0] := 'bi';
// フォームのサイズセット
if StringGrid1.Height + StringGrid1.Top + 10 > cHeight then
clientHeight := StringGrid1.Height + StringGrid1.Top + 10
else
clientHeight := cHeight;
if StringGrid1.Width + StringGrid1.Left + 10 > cheight then
clientWidth := StringGrid1.Width + StringGrid1.Left + 10
else
clientWidth := cWidth;
end;
// 初期設定
procedure TForm1.FormCreate(Sender: TObject);
var
i, k : integer;
begin
cHeight := clientHeight;
cWidth := clientWidth;
memo1.Clear;
// 初期値のセット
setlength(a, N, N);
setlength(b, N);
// 検算用値セット
a[0, 0] := 4; a[0, 1] := 2; a[0, 2] := 6;
a[1, 0] := 1; a[1, 1] := 1; a[1, 2] := 2;
a[2, 0] :=11; a[2, 1] := 7; a[2, 2] := 1;
b[0] := 32; b[1] := 10; b[2] := 77;
GridSet(N + 2, N + 1);
for i := 1 to N do begin
for k := 1 to N do
StringGrid1.Cells[i, k] := floatTostr(a[k - 1, i - 1]);
end;
for k := 1 to N do StringGrid1.Cells[N + 1, k] := floatTostr(b[k - 1]);
end;
// 計算テスト用データー1
// gauss_elimination_basic(基本計算)でも演算エラーはありません。
procedure TForm1.BitBtn1Click(Sender: TObject);
begin
labeledEdit1.Text := '4';
Button2Click(nil);
with StringGrid1 do begin
Cells[1, 1] := inttostr(1);
Cells[2, 1] := inttostr(-1);
Cells[3, 1] := inttostr(-2);
Cells[4, 1] := inttostr(2);
Cells[5, 1] := inttostr(5);
Cells[1, 2] := inttostr(2);
Cells[2, 2] := inttostr(-1);
Cells[3, 2] := inttostr(-3);
Cells[4, 2] := inttostr(3);
Cells[5, 2] := inttostr(10);
Cells[1, 3] := inttostr(-1);
Cells[2, 3] := inttostr(3);
Cells[3, 3] := inttostr(3);
Cells[4, 3] := inttostr(-2);
Cells[5, 3] := inttostr(2);
Cells[1, 4] := inttostr(1);
Cells[2, 4] := inttostr(2);
Cells[3, 4] := inttostr(0);
Cells[4, 4] := inttostr(-1);
Cells[5, 4] := inttostr(-10);
end;
memo1.Clear;
end;
// 計算テスト用データー2
// gauss_elimination_basic(基本計算)でpivotがゼロになり
// 演算エラーが発生します。
procedure TForm1.BitBtn2Click(Sender: TObject);
begin
labeledEdit1.Text := '3';
Button2Click(nil);
with StringGrid1 do begin
Cells[1, 1] := inttostr(3);
Cells[2, 1] := inttostr(6);
Cells[3, 1] := inttostr(2);
Cells[4, 1] := inttostr(32);
Cells[1, 2] := inttostr(1);
Cells[2, 2] := inttostr(2);
Cells[3, 2] := inttostr(8);
Cells[4, 2] := inttostr(40);
Cells[1, 3] := inttostr(7);
Cells[2, 3] := inttostr(3);
Cells[3, 3] := inttostr(3);
Cells[4, 3] := inttostr(35);
end;
memo1.Clear;
if checkbox1.Checked = true then
memo1.Lines.Append('基本プログラムの場合、pivotがゼロになり演算エラーがでます。');
end;
// グリッドから値を取得 ガウスの消去法の解計算
procedure TForm1.Button1Click(Sender: TObject);
var
i, k : integer;
ch : integer;
M : string;
begin
// a項入力
for i := 1 to N do begin
for k := 1 to N do begin
val(StringGrid1.Cells[i, k], a[k - 1, i - 1], ch);
if ch <> 0 then begin
M := '入力データーの列 ' + intTostr(i) + #13#10
+ ' 行 ' + intTostr(k) + 'に間違いがあります。';
application.MessageBox(Pchar(M),'注意',0);
exit;
end;
end;
end;
// b項入力
for i := 1 to N do begin
val(StringGrid1.Cells[N + 1, i], b[i - 1], ch);
if ch <> 0 then begin
M := '入力データーの b行 ' + intTostr(i) + 'に間違いがあります。';
application.MessageBox(Pchar(M),'注意',0);
exit;
end;
end;
memo1.Clear;
if checkbox1.Checked = true then begin
memo1.Lines.Append('基本プログラム');
memo1.Lines.Append(' 演算エラー対策無し');
gauss_elimination_basic; // ガウスの消去法基本
end
else begin
memo1.Lines.Append('演算エラー対策あり');
gauss_elimination; // ガウスの消去法エラーチェックあり
end;
end;
// N元数入力と配列確保、グリッドのセット
procedure TForm1.Button2Click(Sender: TObject);
var
ch : integer;
begin
val(LabeledEdit1.Text, N, ch);
if ch <> 0 then begin
application.MessageBox('N元数の入力値に間違いがあります。', '')
end;
setlength(a, N, N);
setlength(b, N);
GridSet(N + 2, N + 1);
end;
end.
各種プログラム計算例に戻る