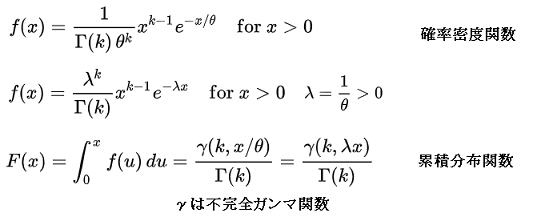
左式の累積分布関数は、下側累積確率です。
Γ(k)は全体なので、1-F(x)で上側累積確率となります。
ガンマ分布
ガンマ分布は、連続確率分布の一種となっています。
ガンマ分布の説明は、難しのて゛、インターネトで検索して下さい。
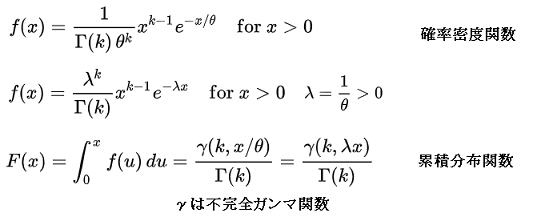
左式の累積分布関数は、下側累積確率です。
Γ(k)は全体なので、1-F(x)で上側累積確率となります。
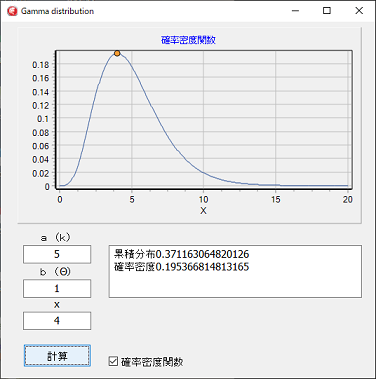
確率密度関数はガンマ関数 累積分布関数は不完全ガンマ関数が計算出来れば、計算可能です。
ここでのプログラムは、C言語辞典 アルゴリズムにあるガンマ関数と不完全ガンマ関数のプログラムを使用しています。
ガンマ関数の計算は、ルーチンを判りやすくする為、ベルヌーイ数を配列にしています。
プログラム
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, VclTee.TeeGDIPlus,
VCLTee.Series, VCLTee.TeEngine, Vcl.ExtCtrls, VCLTee.TeeProcs, VCLTee.Chart,
Vcl.Buttons, system.UITypes, system.Math;
type
TForm1 = class(TForm)
Memo1: TMemo;
LabeledEdit1: TLabeledEdit;
BitBtn1: TBitBtn;
LabeledEdit2: TLabeledEdit;
Chart1: TChart;
Series1: TLineSeries;
Series3: TPointSeries;
CheckBox1: TCheckBox;
LabeledEdit3: TLabeledEdit;
procedure BitBtn1Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
const
//ベルヌーイ数B(2)、B(4)、B(6)、...、B(16)
B : array[1..8] of double = ( 1.0 / 6, // B(2)
-1.0 / 30,
1.0 / 42,
-1.0 / 30,
5.0 / 66,
-691.0 / 2730,
7.0 / 6,
-3617.0 / 510); // B(16)
m: integer = sizeof(B) div sizeof(double);
function Gamma(x: double): double; // ガンマ関数
var
i : integer;
sum : double;
xx, v : double;
xj : double;
lng : double;
ln_sqrt_2pi: double;
begin
ln_sqrt_2pi := ln(sqrt(2 * pi)); // = ln(2 * pi) / 2;
sum := 0;
v := 1;
while x < m do begin
v := v * x;
x := x + 1;
end;
xx := x * x;
xj := x;
lng := ln_sqrt_2pi - x + (x - 0.5) * ln(x) - ln(v);
for i := 1 to m do begin
sum := sum + B[i] / (i * 2 * (2 * i - 1)) / xj;
xj := xj * xx;
end;
result := exp(sum + lng);
end;
// γ(a, x)
function incomplete_gamma(a, x: double): double; // 第1種不完全ガンマ関数
var
k : integer;
term, previous : double;
begin
result := 0;
if x = 0 then exit;
term := exp(a * ln(x) - x) / a;
result := term;
for k := 1 to 1000 do begin
term := term * x / (a + k);
previous := result;
result := result + term;
if result = previous then begin
exit;
end;
end;
Form1.Memo1.Lines.add ('p_gamma(): 収束しません');
end;
procedure TForm1.BitBtn1Click(Sender: TObject);
var
ch : integer;
x, a, b: double;
fx, fsx, ra : double;
dx : double;
i : integer;
begin
val(LabeledEdit1.Text, x, Ch);
if ch <> 0 then begin
MessageDlg('xの値に間違いがあります。', mtInformation,
[mbOk], 0, mbOk);
exit;
end;
if x < 0 then begin
MessageDlg('負数のxは計算出来ません', mtInformation,
[mbOk], 0, mbOk);
exit;
end;
val(LabeledEdit2.Text, a, Ch);
if ch <> 0 then begin
MessageDlg('aの値に間違いがあります。', mtInformation,
[mbOk], 0, mbOk);
exit;
end;
if a <= 0 then begin
MessageDlg('aはゼロより大きくして下さい計算出来ません。', mtInformation,
[mbOk], 0, mbOk);
exit;
end;
val(LabeledEdit3.Text, b, Ch);
if ch <> 0 then begin
MessageDlg('bの値に間違いがあります。', mtInformation,
[mbOk], 0, mbOk);
exit;
end;
if b <= 0 then begin
MessageDlg('bはゼロより大きくして下さい計算出来ません。', mtInformation,
[mbOk], 0, mbOk);
exit;
end;
fsx := incomplete_gamma(a, x / b) / gamma(a); // 累積分布
ra := 1 / b; // λ = 1 / θ
fx := power(ra, a) / gamma(a) * power(x, a - 1) * exp(-ra * x); // 確率密度
Memo1.Clear;
Memo1.Lines.Add('累積分布' + floatTostr(fsx));
Memo1.Lines.Add('確率密度' + floatTostr(fx));
Series1.Clear;
Series3.Clear;
chart1.Title.Text.Clear;
if checkbox1.Checked = True then begin
chart1.Title.Text.Add('確率密度関数');
Series3.AddXY(x, fx);
end
else begin
chart1.Title.Text.Add('累積分布関数');
Series3.AddXY(x, fsx);
end;
dx := 20 / 400;
for i := 0 to 400 do begin
x := dx * i;
if checkbox1.Checked = True then begin
fx := power(ra, a) / gamma(a) * power(x, a - 1) * exp(-ra * x);
Series1.AddXY(x, fx);
end
else
begin
fsx := incomplete_gamma(a, x / b) / gamma(a); // 累積分布
Series1.AddXY(x, fsx);
end;
end;
end;
end.