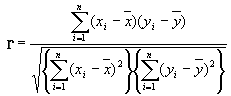Sin回帰+フーリエ変換
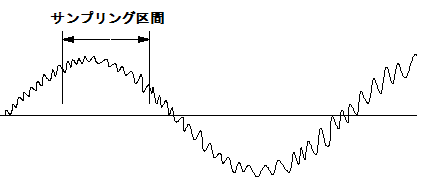 周波数解析の為のデーターのサンプリングが、左図の様に大きく揺れる振動の中の一部分しか取り出せない場合、或いは大きな加速度で加速中の高い周波数の微振動を解析が必要な場合、そのまま解析すると、正しい解析結果が得られない場合があります。
周波数解析の為のデーターのサンプリングが、左図の様に大きく揺れる振動の中の一部分しか取り出せない場合、或いは大きな加速度で加速中の高い周波数の微振動を解析が必要な場合、そのまま解析すると、正しい解析結果が得られない場合があります。
左図の様に直線に沿って振動をしているような場合は、そのまゝ解析すれば正しい結果が得られます。
大きな振動がある場合は、その振動の1サイクル以上のの長さをサンプリングできれば問題なく解析が出来ます。
しかし、上記の様に、あまりにもゆっくりな振動の場合で、その一部分しかサンプリングできない場合、正弦回帰と、フーリエ変換を併用して、周波数の解析をします。
サンプリング例
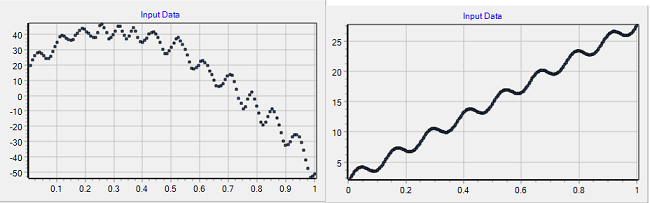
上図がサンプリングしたデーターでこれをそのまま解析をすると、
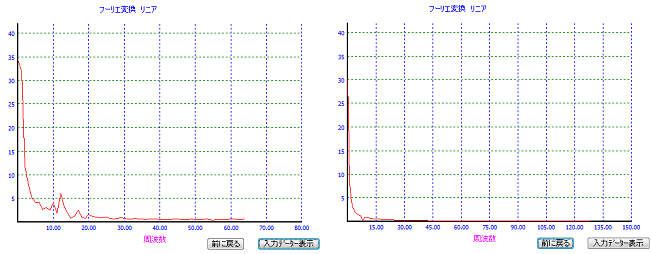
微振動している振動の周波数成分が結果から得ることが出来ません。
そこで、一番上の左側の図のデーターに関して、正弦回帰(SIN回帰)を行ってみます。
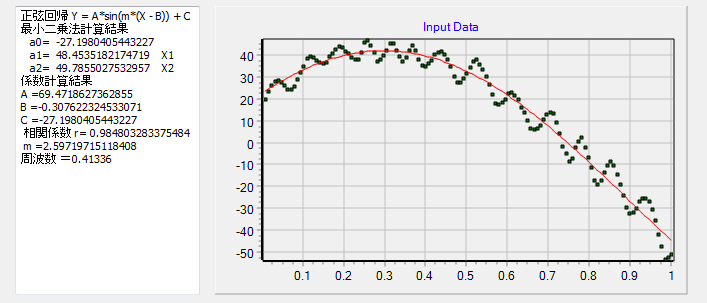
振動周波数0.41336振幅±69,47上での微振動である事が分かります。
そこで、正弦回帰の値を元にして、データーの補正を行います。
計算は簡単で、元データーより、回帰係数から計算した値を差し引くだけです。
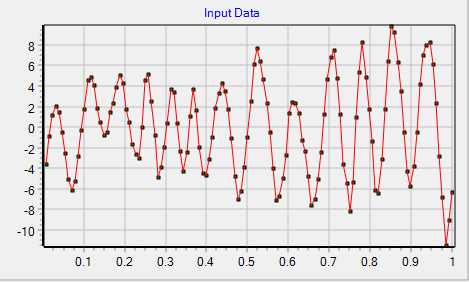
データーの補正により、微振動成分を取り出す事が出来ました。
補正したデーターのフーリエ変換を行ってみます。
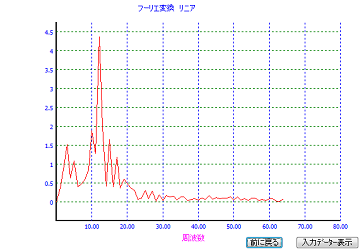
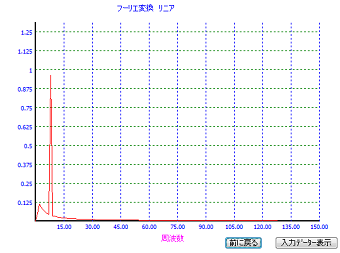
一番上の図左のデーターの場合は振動周波数12Hzにピークがある振動であることが、今度は、はっきりと解析ができています。
上の図右側は、一番上の図右のデーターの解析結果です。こちらは8Hzの振動です。
此処でダウンロード出来るプログラムの使用法について
プログラムを起動すると、データーを入力する為の画面が表示されます。
此処では、解析方法のサンプルプログラムという事で、データーを手入力するか、ファイルから読み込む様になっています。
実際には、測定器から通信、或いは記録媒体で、データーをサンプリングするようにプログラムを変更追加する必要があります。
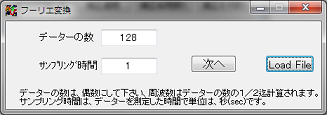
手入力の場合は、データー数と、データーのサンプリング時間を入力して次へボタンをクリックします。
ファイルからデーターを読み込む場合は、Load Fileボタンをクリックして、ファイルオープンダイアログでファイルを指定してデーターを読み込みます。
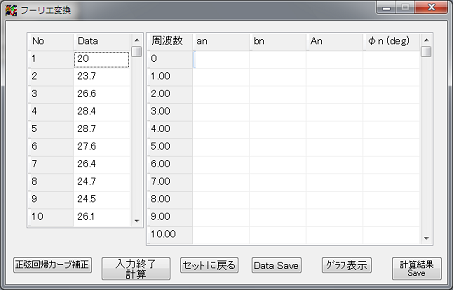
左図 Dataの欄に値を入力します。
ファイルからロードした場合は、値がData欄に表示されます。
ファイルからデーターを再読み込みするめ場合、Data数の変更を行う場合は、セットに戻るボタンをクリックすると、前の画面に戻ります。
読み込んだデーターをグラフ表示する場合は、及び、正弦回帰によるデーターの補正を行う場合は、正弦回帰カープ補正ボタンをクリックします。
このまま、フーリエ変換を行う場合は、入力終了計算ボタンです。
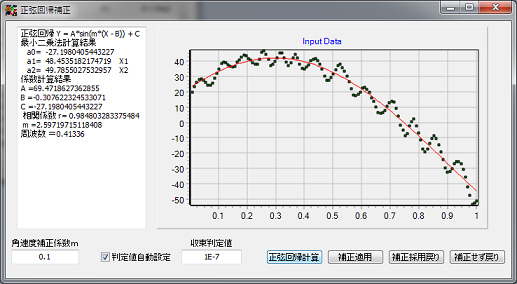
角速度補正係数を設定、左図では 0.1としてあります。
角速度補正係数の値は Rad/sec です。
この値を元にして、Sinの値を求め、正規回帰を行い回帰曲線と、データーの相関係数を求めます。
判定値自動設定にチェックを入れておくと、相関係数が最大になる角速度補正係数を自動的に検索します。
チェックを入れない場合は、相関係数を見ながら、自分で角速度補正係数の値を調整します。
正弦回帰計算 ボタンクリックで、正弦回帰係数が計算されます。
mの初期値によっては、多少違った答えになることがありますが、グラフの全体カーブから大幅に外れていなければ、周波数解析は問題なく出来るでしょう。
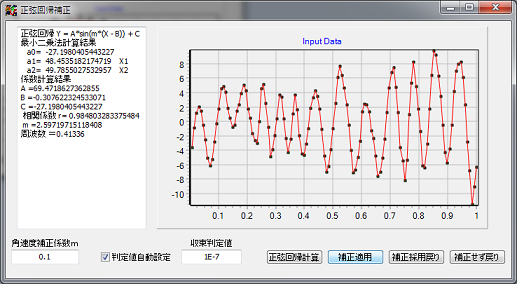 補正適用 ボタンをクリックすると、
補正適用 ボタンをクリックすると、
回帰係数をにより、推定値を計算、元データーから差し引いて、データーの補正をします。
これにより、曲線に乗った振動が、ほぼ直線に乗った振動に変換されます。
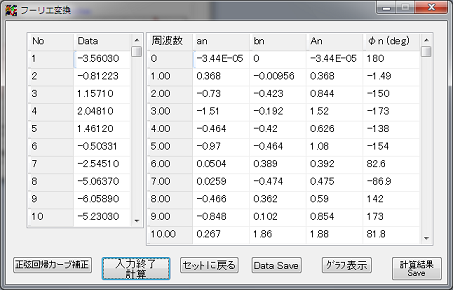
入力データーが補正された値に変更されたら、周波数変換の計算を実行します。
入力終了計算 ボタンをクリックじっこうします。
計算結果が表示されたら、グラフ表示ボタンをクリック、グラフを表示します。
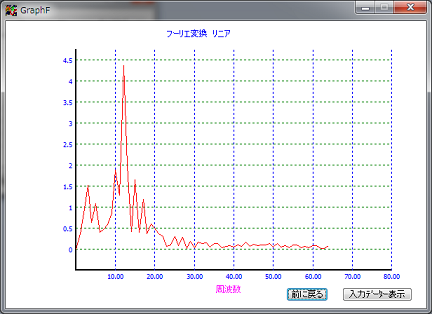
グラフは、リニア値の周波数を表示します。
入力データー表示 ボタンをクリックすることで、周波数変換前のデーターを表示できます。
以上が、データーの正弦補正と、フーリエ変換の計算の流れです。
Sin回帰について
1.最小二乗法により、ある角速度に対するm に対する、Yi=Asin(m(Xi+B)) + C 式の係数A,B,Cを求めます。
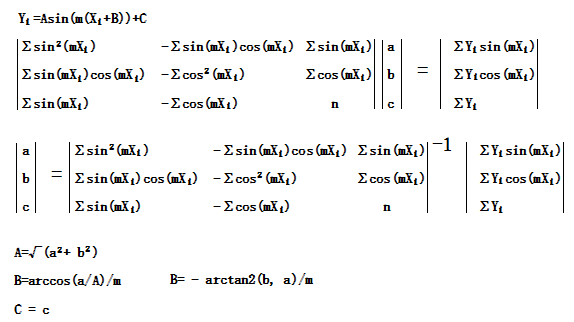 此処のプログラムでは、Sin回帰を使用していますが、Cos回帰の方が一般的なので、Cos回帰を使用しても全く問題はありません。
此処のプログラムでは、Sin回帰を使用していますが、Cos回帰の方が一般的なので、Cos回帰を使用しても全く問題はありません。
むしろ、Cos回帰の方が良いのかも知れません。
回帰係数はSin関数の最小二乗法で求めます。
Cos関数に変更する場合は、行列式のSinとCosを入れ替えるだけです。
Xiは、時間軸秒単位、mは角速度です。
角速度は、最初適当な値をいれます。
ここのプログラムでは、デフォルト値として0.1をセットしています。
最小二乗法では、入れた角速度にたいする各係数値A,B,Cが求まるだけです。
このままでは、m角速度の値は、求める事が出来ません。
2.Xiの値を次の計算で変換して相関係数を求めます。
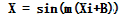
3.相関係数 r の計算、Xiの値は、最初のXiの値ではなく、sin(m(Xi+B))で変換した値です。
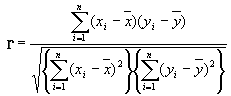
4.相関係数 r の値が最大になる様に、角速度mの値を変化させて最初から繰り返し計算します。
相関係数が最大になったところを、Sin回帰係数の角速度とします。
初期に与えた、角速度の値によっては、角速度の値が変ることもありますが、補正後の周波数変換の値はあまり変化しないでしょう。
フーリエ変換は、データーの数がいくつでも良いようにDFTを使用しています。
最小二乗法プログラム例
此処でダウンロード出来るプログラムでは、逆行列計算にガウスの消去法(掃き出し法)を使用していますが、下記のプログラム例では、通常の計算方法を使用しています。
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls;
type
TForm1 = class(TForm)
Button1: TButton;
Memo1: TMemo;
Memo2: TMemo;
procedure FormCreate(Sender: TObject);
procedure Button1Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses
math;
var
n: integer; // データー数
a: array[0..16] of double; // データー Y
T: array[0..16] of double; // 時間軸 X
Ss2, Ssc, Ss, Sc2, Sc, SYs, Syc, Sy: double; // Σ値
m: double; // 角速度
b: array[0..2] of array[0..2] of double; // 3x3 行列
c: array[0..2] of array[0..2] of double; // 3x3 逆行列
Detb : double; // det
at, bt, ct: double; // パラメータ a,b,c
Al, Bl, Cl: double; // sin回帰係数
procedure TForm1.Button1Click(Sender: TObject);
var
II,JJ: integer;
LL : string;
Leng: Integer;
begin
// m := pi;
m := 2 * pi; // 角速度の設定
n := 17; // データー数
// sinカーブデーターの作成
for II := 0 to n -1 do
a[II] := sin(II * 2 * pi / (n-1) + 2 * pi / 8);
// 行列用データーの計算
for II := 0 to n -1 do begin
// データーの生成
a[II] := a[II] + 0.3;
T[II] := II / (n - 1);
// Σ値の計算
Ss2 := Ss2 + power(sin(T[II] * m), 2);
Ssc := Ssc + sin(T[II] * m) * cos(T[II] * m);
Ss := Ss + sin(T[II] * m);
Sc2 := Sc2 + power(cos(T[II] * m), 2);
Sc := Sc + cos(T[II] * m);
Sys := Sys + a[II] * sin(T[II] * m);
Syc := Syc + a[II] * cos(T[II] * m);
Sy := Sy + a[II];
end;
// 行列に割付
b[0,0] := Ss2; b[0,1] := -Ssc; b[0,2] := Ss;
b[1,0] := Ssc; b[1,1] := -Sc2; b[1,2] := Sc;
b[2,0] := Ss; b[2,1] := -Sc; b[2,2] := n;
// DetBの計算
Detb := b[0,0] * b[1,1] * b[2,2]
+ b[1,0] * b[2,1] * b[0,2]
+ b[2,0] * b[0,1] * b[1,2]
- b[0,0] * b[2,1] * b[1,2]
- b[2,0] * b[1,1] * b[0,2]
- b[1,0] * b[0,1] * b[2,2];
// Detbがゼロだったら逆行列なし
if Detb = 0 then begin
LL := '逆行列なし';
Memo2.Lines.Add(LL);
exit;
end;
// 逆行列の計算
c[0,0] := b[1,1] * b[2,2] - b[1,2] * b[2,1];
c[0,1] := b[0,2] * b[2,1] - b[0,1] * b[2,2];
c[0,2] := b[0,1] * b[1,2] - b[0,2] * b[1,1];
c[1,0] := b[1,2] * b[2,0] - b[1,0] * b[2,2];
c[1,1] := b[0,0] * b[2,2] - b[0,2] * b[2,0];
c[1,2] := b[0,2] * b[1,0] - b[0,0] * b[1,2];
c[2,0] := b[1,0] * b[2,1] - b[1,1] * b[2,0];
c[2,1] := b[0,1] * b[2,0] - b[0,0] * b[2,1];
c[2,2] := b[0,0] * b[1,1] - b[0,1] * b[1,0];
// DetBで除算
for II := 0 to 2 do
for JJ := 0 to 2 do
c[II, jj] := C[II,JJ] / detB;
// パラメーター a,b,cの計算
at := c[0,0] * Sys + c[0,1] * Syc + c[0,2] * Sy;
bt := c[1,0] * Sys + c[1,1] * Syc + c[1,2] * Sy;
ct := c[2,0] * sys + c[2,1] * Syc + c[2,2] * Sy;
// 回帰係数の計算
Al := sqrt(at * at + bt * bt); // Aの計算
Bl := -arctan2(bt, at) / m; // θの計算
// Bl := arccos(at/Al) / m; // θの計算前行と同じ
Cl := ct; // 係数C
// 係数の表示
memo1.Clear;
memo2.Clear;
LL := 'Y = A(sin(m(θ+X)) + C';
Memo1.Lines.Add(LL);
LL := 'A = ' + floatTostr(Al);
Memo1.Lines.Add(LL);
LL := 'θ= ' + floatTostr(Bl);
Memo1.Lines.Add(LL);
LL := 'C = ' + floatTostr(Cl);
Memo1.Lines.Add(LL);
// データーの表示
LL := 'データー';
Memo2.Lines.Add(LL);
LL := '角速度係数m= ' + floatTostr(m) + ' rad/sec';
Memo2.Lines.Add(LL);
LL := '時間 X データー Y';
Memo2.Lines.Add(LL);
for II := 0 to n -1 do begin
LL := floatTostr(T[II]);
Leng := Length(LL);
Leng := 20 - leng;
for JJ := 0 to leng do LL := LL + ' ';
LL := LL + floatTostr(a[II]);
Memo2.Lines.Add(LL);
end;
end;
procedure TForm1.FormCreate(Sender: TObject);
begin
{
a[0] := 0;
a[1] := 0.382683;
a[2] := 0.707107;
a[3] := 0.92383 ;
a[4] := 1;
a[5] := 0.92387;
a[6] := 0.707107;
a[7] := 0.382683;
a[8] := 0;
a[9] := -0.382683;
a[10] := -0.70711;
a[11] := -0.92388;
a[12] := -1;
a[13] := -0.92388;
a[14] := -0.70711;
a[15] := -0.38268;
a[16] := 0;
}
end;
end.
 fourier2.zip
fourier2.zip
各種プログラム計算例に戻る
 周波数解析の為のデーターのサンプリングが、左図の様に大きく揺れる振動の中の一部分しか取り出せない場合、或いは大きな加速度で加速中の高い周波数の微振動を解析が必要な場合、そのまま解析すると、正しい解析結果が得られない場合があります。
周波数解析の為のデーターのサンプリングが、左図の様に大きく揺れる振動の中の一部分しか取り出せない場合、或いは大きな加速度で加速中の高い周波数の微振動を解析が必要な場合、そのまま解析すると、正しい解析結果が得られない場合があります。









 補正適用 ボタンをクリックすると、
補正適用 ボタンをクリックすると、

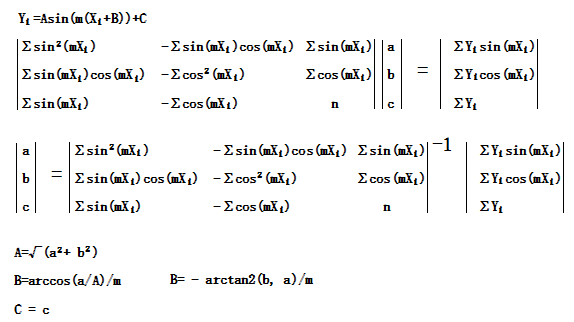 此処のプログラムでは、Sin回帰を使用していますが、Cos回帰の方が一般的なので、Cos回帰を使用しても全く問題はありません。
此処のプログラムでは、Sin回帰を使用していますが、Cos回帰の方が一般的なので、Cos回帰を使用しても全く問題はありません。