2020/05/31
カイザー窓関数を追加しました。
2020/05/22 プログラム修正
FFTルーチンの数を増やし、更に、FFTルーチン側に窓関数を追加しました。
2020/05/11 プログラム修正
フーリエ変換プログラムに、FFTルーチンを追加しました。
FFTルーチンは、画像処理に有ったものを、一次元用に変更して追加しました。
又、少し計算手順の違うFFTのプログラムを、速度比較の為、追加しました。
新しいFFTの方が２割程度早くなっています。
フーリエ変換
フーリエ変換は、全ての波形は、正弦波の重なりとして表現できるとして生まれた変換です。
逆変換をすれば、ほぼ元の値（波形）に戻すことができ、デジタルの離散データーは完全に元の値に戻すことも可能です。
周波数変換時は、cos,sinの角度を右回り（時計回り）で計算し、逆変換時は左回りで計算する決まりとなっています。
位相角の方向を問題にしなければ、どちら回りで計算しても同じ結果が得られ、逆変換は、周波数変換時とは逆の方向で計算すれば良いだけです。
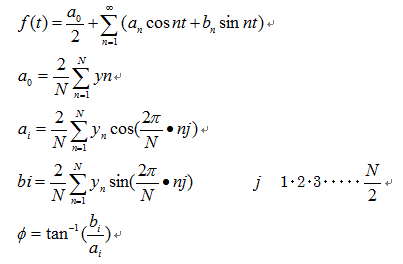フーリエ変換は今ではありふれた計算で、インターネットで探せば、必ず直ぐにサンプルプログラムが見つかるでしょう。
測定器にも、フーリエ変換のルーチンが組み込まれてるのがあります。
筆者が、最初にフーリエ変換を利用した時には、フーリエ変換を組み込んだ測定器は、高価なものでした。
その時に、BASICで、フーリエ変換のプログラムを組み、データーを手入力して解析をしたりしました。
測定器には、アルゴリズムで解析する、高速変換がありますが、実際の測定では、あまり速度を要求される事はあまりありません。
測定器から、RS232Cでデーターをサンプリングし、解析しても良いでしょう。
本当に高速性が要求される場合は、ＦＦＴ専用の測定器を使用するか、ＦＦＴを組み込んであるオシロを使用しましょう。
振動の解析には、フーリエ変換が必須です。
振動の解析で、よくある間違いは、加速度をそのままフーリエ変換してしまうことです、振動は、必ず移動距離（振幅）で行うべきです。
加速度は、積分して速度に、速度を更に積分して、距離（振幅）にしてフーリエ変換をします。
二階積分（二重積分）となるらしいですが。
振動の測定器には、ＦＦＴが最初から組み込まれていて、殆どリアルタイムに近い状態で、周波数が表示されます。
振動のセンサーとしては、加速度計が広く使用されていますが、加速度計はノイズを拾いやすく、注意が必要ですが、二階積分を行うことで、細かいノイズは殆ど取り除かれます。
特に注意をしなければならないのは、計算できる周波数より高い周波数が、サンプリング時に存在する場合は計算出来る周波数より高い部分は、フィルターにより取り除く必要があります。
サンプリング時間より長い周期の低い周波数がある場合も、低い周波数の値を取り除いたほうが正確に変換することができます。
此処でのフーリエ変換は、信号に対してですが、画像処理には画像のフーリエ変換もあり、基本的な計算は同じですが、画像処理は二次元のフーリエ変換を行います。
周波数変換について
フーリエ変換については、難しい理論が書いてあり、やさしく解説をしている資料は少ないです。
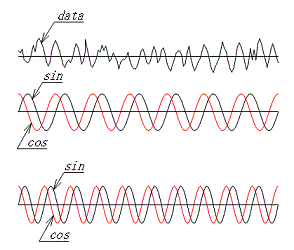
一定間隔でサンプリングしたデーターをフーリエ変換して周波数分析を行う場合、ある一つの周波数に着目して考えると、そのデーターの波形が、着目した周波数の波形にいかに近似しているかの相関値を計算していることになります。
サンプリングしたデーターと、 正弦波 を時間軸で追って乗算し総和を計算、平均値を求めます。
統計的手法の相関値と違うのは、位相を９０度ずらした波形とも相関を計算し、波形開始点の角度を求めているのと、サンプリングデーターの値により、相関値にデーターの値が寄与することです。
一般的統計的手法では、完全に一致した場合は１ですが、フーリエ変換の場合は、サンプリングデーターの波形値から導き出された値となります。
サンプリングデーターの波形が大きくなれば、変換値が大きくなります。
サンプリングデーターが完全な正弦波でありピーク値が±１であれば変換値は１になり±１．４であれば１．４になります。
周波数変換された周波数、値と角度から、逆変換を行うと、元のデーターに近似した波形を得ることができます。
デジタルの離散データーの場合は、元の値に戻すことも可能です。
実際の計算では直流成分と一番高い周波数（データー数の１／２）以外は１／２の値として計算されます、これはＤＦＴ、ＦＦＴ変換の計算アルゴリズムによるものです。
そこで、周波数変換のデーターをそのまま利用する場合は、ＤＦＴ、ＦＦＴ計算結果を二倍します。
離散データーのフーリエ変換での問題は、計算で得られた値をそのまま、鵜呑みにしてはいけない事です。
単一のきれいな正弦波でも、サンプリングする時間と間隔によって、並んだ二個の値と近くの小さな値に分かれてしまう事があります。
サンプリングした時間と、サンプリング間隔から計算される周波数の中間に位置する周波数の場合、その周波数を計算から得ることが出来ない為です。
又、サンプリング間隔より高い周波数のものから、サンプリングすると、低い周波数としてサンプリングしてしまいます。
計算出来る周波数より高いものは、サンプリングする前に、フィルターでカットしておく必要があります。
何度もサンプリング出来る場合は、元の波形を見ながら、サンプリング間隔、サンプル時間を変更して解析すると良いでしょう。
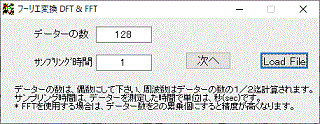左図は此処でのプログラムの実行最初の画面です。
データーの入力は、ファイルからの入力か、手動での入力しかありません。
手動の場合は、データー数と、サンプリング時間を入力し次へで編集計算画面へ進みます。
ファイルから入力した場合は、データー数とサンプリング時間がファイルから読み込まれます。
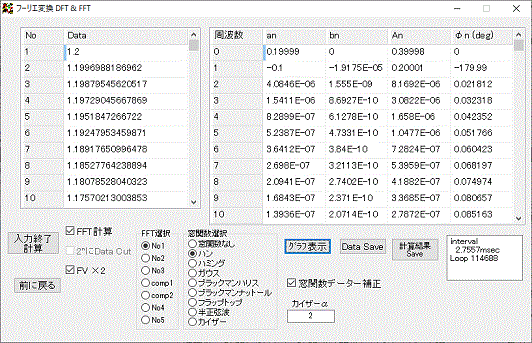入力したデーターを編集する場合は、Ｄａｔａ欄の値を変更します。
ＦＦＴ計算のチェックボックスにチェックを入れなければ、ＤＦＴで計算され、チェックを入れるとＦＦＴで計算されます。
ＦＦＴには、七つのルーチンが用意されているので、計算選択のチェックボックスで選択が出来ます。
単にＦＦＴのプログラムの計算速度確認の為に用意しました。
ＦＦＴの計算を選択した場合、データー数が２ｎの個数になっていない場合、２ｎにＤａｔａ Ｃｕｔのチェックボックスが入力可能になります。
此処にチェックを入れると、データーが２ｎにカットされます。
チェックを入れない場合は、２ｎになる様に、データーの最後にゼロが追加されます。
この時の計算結果はＤＦＴの計算とは一致しません。
元のデーターの数が、２ｎの場合は、ほぼ同じになりますが、ゼロ近辺の値は、演算誤差により少し違った値が表示されます。
ＦＶ×２のチェックボックスは、リニア値に変換された値全体を二倍にするかどうかの選択です。
DFT、FFTルーチンの実行時間の測定が出来る様にしてあります。
複素数の計算もあります、計算式は簡単に見えますが、実際のルーチンは長くなるため速度は改善されません。
色々テストした結果、Ｎｏ２の計算が安定して早い結果を示します。
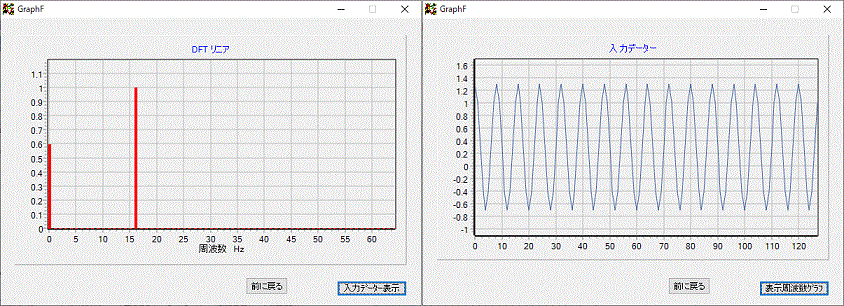左図の棒グラフは、周波数変換のグラフです。
右側が、元の離散データーで、０．３程プラス側にシフトした±1のｃｏｓ波です。
周波数変換リニア値を二倍して表示しているので、周波数ゼロである平均値は倍の値になっていて、１６ＨＺの値は、±1の１の値を表示しています。
サンプリング時間が１秒なので、データー数１２８個に対して、１／２の６4HZが解析できる最高周波数となります。
フーリエ変換の最低周波数は、サンプル時間内でのサイクル数が１ですが、それより低い場合は、正弦回帰を利用してみるのも良いでしょう。
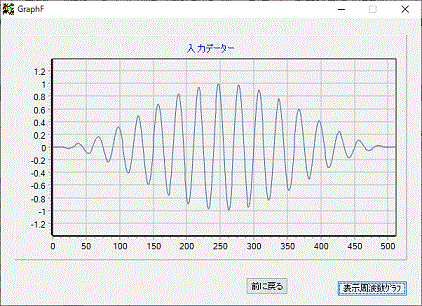左図は、データーに窓関数を設定した場合の値です。
FFTの計算は、連続した波形（サンプリング時間内の波形の数が整数）が基本となっていますが、実測する場合、サンプリング時間の関係で、波形の整数倍でサンプリングできるとは限らないため、きれいな正弦波であっても、単一波形として解析出来ない場合が殆どです。
そこで、窓関数を使用して解析の精度を上げます。
元の波形が正弦波の場合は良いのですが、矩形波に近い場合は、逆に精度が悪くなることがあるので注意が必要です。
DFT計算の場合も、窓関数を使用しても良いのですが、ＤＦＴの場合サンプリング数を自由に出来るので、解析した結果を見ながら、計算するサンプル数を短くして、サンプルデーターの波形の数が整数倍になるように調整してみるもの良いでしょう。
窓関数に色々な種類がありますが、カイザーの窓関数は、窓の係数を変更して、窓の形状を変更できるのでこれ一つあれば良いかと思います。
但し、窓の計算に時間が掛かるので、データー数が決まったら最初にテーブルとして生成しておくと良いでしょう。
周波数解析用のサンプルデーターは、波形と数式 のプログラムでファイル形式として作ることができます。
プログラム
DFTのプログラムは、データー数がいくつでも使用できますが、FFTは２ｎに成っていないと使用できません。
そこで、２ｎに成っていない場合は、後ろにゼロを追加して、２ｎにするか、短くカットして、２ｎにしてFFTの計算が使用できるようにしてみました。
画像の処理に利用する場合は、周波数変換後、又、画像に戻すので、周波数に変換した値を問題にすることはないのですが、一次元の周波数そのものを利用する場合は、データーのカットをしたりゼロの追加をすると、Dデーターの加工をしない、DFTでの計算とは同じ答えを得ることは出来ません。
FFTの実行時間を測定してみると、計算式は変わらないのですが、少しの工夫で大きく実行時間が変動します。
此処の計算で早いと出たＦＦＴのルーチンを二次元の画像計算に使用しても、早くなるとは限らないようですが、その理由はわかりません。
unit Fourier;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, Buttons, Grids, ExtCtrls, System.UITypes;
// 複素数構造体
type
Tcmplx = record
real : double;
Imaginary : double;
end;
type
TFourierF = class(TForm)
OpenDialog1: TOpenDialog;
SaveDialog1: TSaveDialog;
SaveDialog2: TSaveDialog;
Label1: TLabel;
Label2: TLabel;
BitBtn1: TBitBtn;
BitBtn4: TBitBtn;
StringGrid1: TStringGrid;
StringGrid2: TStringGrid;
BitBtn2: TBitBtn;
BitBtn3: TBitBtn;
BitBtn5: TBitBtn;
BitBtn6: TBitBtn;
BitBtn7: TBitBtn;
Label3: TLabel;
Edit1: TEdit;
Edit2: TEdit;
CheckBox1: TCheckBox;
CheckBox2: TCheckBox;
CheckBox4: TCheckBox;
Memo1: TMemo;
RadioGroup1: TRadioGroup;
RadioGroup2: TRadioGroup;
CheckBox3: TCheckBox;
KaiserEdit: TLabeledEdit;
procedure FormCreate(Sender: TObject);
procedure BitBtn1Click(Sender: TObject);
procedure BitBtn3Click(Sender: TObject);
procedure BitBtn2Click(Sender: TObject);
procedure StringGrid1KeyPress(Sender: TObject; var Key: Char);
procedure BitBtn5Click(Sender: TObject);
procedure BitBtn4Click(Sender: TObject);
procedure StringGrid2DrawCell(Sender: TObject; ACol, ARow: Integer;
Rect: TRect; State: TGridDrawState);
procedure BitBtn6Click(Sender: TObject);
procedure BitBtn7Click(Sender: TObject);
procedure StringGrid1DrawCell(Sender: TObject; ACol, ARow: Integer;
Rect: TRect; State: TGridDrawState);
procedure Edit1Change(Sender: TObject);
procedure Edit2Change(Sender: TObject);
procedure Edit1KeyPress(Sender: TObject; var Key: Char);
procedure Edit2KeyPress(Sender: TObject; var Key: Char);
procedure CheckBox1MouseUp(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y: Integer);
private
{ Private 宣言 }
FFrequency: int64; // ストップウォッチ用 基準クロック
FStart: int64; // スタートカウンター値
FStop: int64; // ストップカウンター値
procedure Ndisp; // データー数入力画面設定
procedure Ddisp; // データー入力 及び 計算
function Edit1Check:integer; // Edit1入力チェック
function Edit2Check:integer; // Edit2入力チェック
function incheck(Indat: string; var data: double): Boolean; // 入力チェック
procedure FourierCalc; // フーリエ変換
procedure CalcSave; // 計算結果ファイル
procedure fft1core(length, ex, inv: integer; var a_rl, a_im, sin_tbl, cos_tbl, buf: array of double);
procedure birv(var a: array of double; length, ex: Integer; var b: array of double);
procedure StringGrid2Set;
procedure fft2(length, inv: integer; var a_rl, a_im, sin_tbl, cos_tbl: array of double;
var m: array of integer);
procedure fft3(length, ex, inv: integer; var a_rl, a_im, sin_tbl, cos_tbl: array of double);
procedure Start; // stopwatch strat
function Stop: extended; // stopwatch stop
procedure F(n, s, q, d: integer; var x: array of Tcmplx);
procedure fftcmp(n: integer; var x: array of Tcmplx);
procedure fftcmp2(n: integer; var x: array of Tcmplx; var sin_tbl, cos_tbl: array of double);
procedure fft4(n: integer; var xr, xi, sin_tbl, cos_tbl: array of double);
procedure fftNo5(n, ex: integer; var xr, xi, sin_tbl, cos_tbl: array of double);
public
{ Public 宣言 }
end;
var
FourierF : TFourierF;
N : integer; // データー数
NF : integer; // FFT データー数
stwT : extended; // stopwatch
BXindat: array of Double; // 入力データ グラフ表示用
implementation
{$R *.dfm}
uses graph, math;
const
No1 = 0;
No2 = 1;
No3 = 2;
comp1 = 3;
comp2 = 4;
No4 = 5;
No5 = 6;
non = 0;
Hanning = 1;
Hamming = 2;
Gauss = 3;
BlackmanHarris = 4;
BlackmanNuttall = 5;
FlapTop = 6;
HalfSin = 7;
han = 1 / 0.5;
ham = 1 / 0.53997;
gus = 1 / 0.85561;
har = 1 / 0.35873;
nut = 1 / 0.36356;
fla = 1 / 0.9994;
hal = 1 / 0.63658;
var
F1, F2 : TextFile;
NFF : integer; // FFT データー数
T : double; // サンプリング時間
TF : double; // FFT サンプリング時間
Calcd : Boolean = False; // 計算したフラグ
Loop : integer;
Xindat: array of Double; // 入力データ
an: array of Double; // con変換 実数部
bn: array of Double; // sin変換 虚数部
Fv: array of Double; // リニアレベル
Qf: array of Double; // 位相角
dpic: array of Double; // cos(2pi / N J)
dpis: array of Double; // sin(2pi / N J)
buf_x: array of Double; // 作業用バッファ
m : array of integer; // bit反転処理用
x : array of Tcmplx; // 複素数
// ストップウォッチスタート
procedure TFourierF.Start;
begin
QueryPerformanceFrequency(FFrequency); // 基準クロック取得
QueryPerformanceCounter(FStart); // スタート時カウンター値
end;
// ストップウォッチ停止
function TFourierF.Stop: extended;
begin
QueryPerformanceCounter(FStop); // ストップ時カウンター時
if FFrequency > 0 then // クロックの値を取得出来ていたら時間計算
result := (FStop - FStart) * 1000 / FFrequency
else result := -1;
end;
//------------------------------------------------------------------------------
// データの開始と終了が連続でない場合はいずれかの窓関数処理を行ないます。
// 第１種変形ベッセル関数
function BesselI0(x: double): double;
const
NMAX = 100; // Doubleでの桁落ち限度
var
M : integer;
J: Integer;
B, S: double;
begin
M := NMAX;
B := 1; // J = 0
S := B;
for J := 1 to M do begin
B := B / (J * J); // 1/(m!Γ(J))
S := S + B * power(X / 2, 2 * J); // Σ
end;
result := S;
end;
// カイザー窓関数
procedure WinKaiser(a: double; var data: array of Double);
var
n, i : integer;
begin
n := length(data);
for i := 0 to n - 1 do begin
data[i] := BesselI0(pi * a * sqrt(1 - power(2 * i / (n - 1) - 1, 2)))
/ BesselI0(pi * a) * data[i];
end;
end;
// ハン窓関数
procedure WinHanning(var data: array of Double);
var i, n: integer;
begin
n :=length(data);
for i := 0 to n - 1 do begin
data[i] :=(
0.5 - 0.5 * Cos(2 * Pi * i / (n - 1))
) * data[i];
end;
end;
// ハミング窓関数
procedure WinHamming(var data: array of Double);
var
i, n: integer;
begin
n := length(data);
for i := 0 to n-1 do begin
data[i] := (
0.54 - 0.46 * Cos(2 * Pi * i / (n - 1))
) * data[i];
end;
end;
// ガウス窓関数 m = 1～3σ
procedure WinGauss(var data: array of Double; m: integer = 1);
var
i, n: integer;
begin
n := length(data);
for i := 0 to n - 1 do begin
data[i] := Exp(
-2 * power(m, 2) / power(n - 1, 2) * power(i - (n - 1) / 2,2)
) * data[i];
end;
end;
// ブラックマンハリス窓関数
procedure WinBlackmanHarris(var data: array of Double);
var
i, n: integer;
begin
n:=length(data);
for i := 0 to n-1 do begin
data[i] := (0.35875 - 0.48829 * cos(2 * Pi * i / (n - 1))
+ 0.14128 * cos(4 * Pi * i / (n - 1))
-0.01168 * cos(6 * Pi * i / (n - 1))
) * data[i];
end;
end;
// ブラックマンナットール窓関数
procedure WinBlackmanNuttall(var data: array of Double);
var
i, n: integer;
begin
n := length(data);
for i := 0 to n - 1 do begin
data[i] := (0.3635819 - 0.4891775 * cos(2 * Pi * i / (n - 1))
+ 0.1365995 * cos(4 * Pi * i / (n - 1))
- 0.0106411 * cos(6 * Pi * i / (n - 1))
) * data[i];
end;
end;
// フラップトップ窓関数
procedure WinFlapTop(var data: array of Double);
var
i, n: integer;
begin
n :=length(data);
for i := 0 to n - 1 do begin
data[i] := (1 - 1.930 * Cos(2 * Pi * i / (n - 1))
+ 1.290 * Cos(4 * Pi * i / (n - 1))
- 0.388 * Cos(6 * Pi * i / (n - 1))
+0.032 * Cos(8 * Pi * i / (n - 1))
) * data[i];
end;
end;
// 半正弦波窓関数
procedure WinHalfSin(var data: array of Double);
var
i, n: integer;
begin
n := length(data);
for i := 0 to n - 1 do begin
data[i] := Sin(pi * i / (n - 1)) * data[i];
end;
end;
//----------------------------------------------------------------------------
// 複素数の生成
function Varcomplex(a, b: double): Tcmplx;
begin
result.real := a;
result.Imaginary := b;
end;
// 複素数加算
function cadd(a, b: Tcmplx): Tcmplx;
begin
result.real := a.real + b.real;
result.Imaginary := a.Imaginary + b.Imaginary;
end;
// 複素数減算
function csub(a, b: Tcmplx): Tcmplx;
begin
result.real := a.real - b.real;
result.Imaginary := a.Imaginary - b.Imaginary;
end;
// 複素数乗算
function cmul(a, b: Tcmplx): Tcmplx;
begin
result.real := a.real * b.real - a.Imaginary * b.Imaginary;
result.Imaginary := a.real * b.Imaginary + a.Imaginary * b.real;
end;
//---------------------------comp No2 ---------------------------
// n データー長
// x データー複素数配列
// sin_tbl, cos_tbl sin cos テーブル
//---------------------------------------------------------------
procedure TFourierF.fftcmp2(n: integer; var x: array of Tcmplx; var sin_tbl, cos_tbl: array of double);
var
comp, compth: Tcmplx;
i, ia, ib, j, k, ns, arg : integer;
begin
ns := n div 2;
while ns >= 1 do begin
arg := 0;
j := 0;
while j < n do begin
k := n div 4;
compth := Varcomplex(cos_tbl[arg], sin_tbl[arg]);
for ia := j to j + ns - 1 do begin
ib := ia + ns;
comp := cmul(x[ib], compth);
x[ib] := csub(x[ia], comp);
x[ia] := cadd(x[ia], comp);
inc(loop);
end;
while k <= arg do begin
arg := arg - k;
k := k div 2;
if k = 0 then break;
end;
arg := arg + k;
j := j + ns + ns;
end;
ns := ns div 2;
end;
for i := 0 to n - 1 do begin
x[i].real := x[i].real / NFF;
x[i].Imaginary := x[i].Imaginary / NFF;
end;
j := 1; // ビット反転処理
for i := 1 to n - 1 do begin
if i <= j then begin
comp := x[i - 1];
x[i - 1] := x[j - 1];
x[j - 1] := comp;
end;
k := n div 2;
while k < j do begin
j := j - k;
k := k div 2;
end;
j := j + k;
end;
end;
//------------------ cmp No1 -Cooley-Tukey-------------------------
// n データー長
// x データー長 複素数配列
//-----------------------------------------------------------------
procedure TFourierF.fftcmp(n: integer; var x: array of Tcmplx);
var
i : integer;
a : double;
begin
F(n, 1, 0, 0, x);
a := 1 / NFF;
for i := 0 to n - 1 do begin
x[i].real := x[i].real * a;
x[i].Imaginary := x[i].Imaginary * a;
end;
end;
//---------------再起呼び出し------------------------------
procedure TFourierF.F(n, s, q, d: integer; var x: array of Tcmplx);
var
m, p: integer;
theta0: double;
a, b, wp, tmp: Tcmplx;
procedure swap(var sa, sb: Tcmplx);
begin
tmp := sa;
sa := sb;
sb := tmp;
end;
begin
m := n div 2;
theta0 := - 2 * pi / n;
if N > 1 then begin
for p := 0 to m - 1 do begin
wp := Varcomplex(cos(p * theta0), sin(p * theta0));
a := x[q + p + 0];
b := x[q + p + m];
x[q + p + 0] := cadd(a, b);
tmp := csub(a, b);
x[q + p + m] := cmul(tmp, wp);
inc(loop);
end;
F(N div 2, 2 * s, q + 0, d + 0, x); // 偶数位置成分
F(N div 2, 2 * s, q + m, d + s, x); // 奇数位置成分
end
else if (q > d) then swap(x[q], x[d]);
end;
//----------------------------------------------------------------------------
//------ No1 -- １次元ＦＦＴの計算の核になる部分 ---------------------------
// a_rl: データ実数部（入出力兼用）
// a_im: データ虚数部（入出力兼用）
// length: データー個数
// ex: データ個数を２の累乗で与えます(2のex乗個）
// sin_tbl: SIN計算用テーブル
// cos_tbl: COS計算用テーブル
// inv 変換 0 逆変換 1
// 2048 で 0.27msec
//-----------------------------------------------------------------------------
procedure TFourierF.fft1core(length, ex, inv: integer; var a_rl, a_im, sin_tbl, cos_tbl, buf: array of double);
var
i, j, k, w, j1, j2 : Integer;
numb, lenb, timb : Integer;
xr, xi, nrml : Double;
begin
numb := 1;
lenb := length;
for i := 0 to ex - 1 do begin
lenb := lenb div 2;
timb := 0;
for j := 0 to numb - 1 do begin
w := 0;
for k := 0 to lenb - 1 do begin
j1 := timb + k;
j2 := j1 + lenb;
xr := a_rl[j1] - a_rl[j2];
xi := a_im[j1] - a_im[j2];
a_rl[j1] := a_rl[j1] + a_rl[j2];
a_im[j1] := a_im[j1] + a_im[j2];
a_rl[j2] := xr * cos_tbl[w] - xi * sin_tbl[w];
a_im[j2] := xr * sin_tbl[w] + xi * cos_tbl[w];
w := w + numb;
inc(loop);
end;
timb := timb + 2 * lenb;
end;
numb := numb * 2;
end;
birv(a_rl, length, ex, buf); // 実数データの並べ換え
birv(a_im, length, ex, buf); // 虚数データの並べ換え
if inv = 0 then begin // 周波数変換時はデーター数で除算 逆変換時はなし
nrml := 1 / NFF; // Σ値を実質のデーター数で除算します。
for i := 0 to length - 1 do begin
a_rl[i] := a_rl[i] * nrml;
a_im[i] := a_im[i] * nrml;
end;
end;
end;
//--- birv --- データの並べ換え ビット反転処理---------------------------------
// a: データの配列
// length: データ個数
// ex: データ個数を２の累乗で与えます(2のex乗個）
// b: 作業用バッファ
//-----------------------------------------------------------------------------
procedure TFourierF.birv(var a: array of double; length, ex: Integer; var b: array of double);
var
i, ii, k, bit : Integer;
begin
for i := 0 to length - 1 do begin
ii := i;
bit:= 0;
for k := 0 to ex do begin
bit := (ii and 1) or bit;
if k = ex - 1 then break;
bit := bit shl 1;
ii := ii shr 1;
end;
b[i] := a[bit];
end;
for i := 0 to length - 1 do a[i] := b[i];
end;
// ------------------------No2 FFT計算 ------------------------------
// a_rl: データ実数部（入出力兼用）
// a_im: データ虚数部（入出力兼用）
// length: データー個数
// inv: 変換フラグ 0 変換 1 逆変換
// 2048 で 0,21msec
// -----------------------------------------------------------------
procedure TFourierF.fft2(length, inv: integer; var a_rl, a_im, sin_tbl, cos_tbl: array of double;
var m: array of integer);
var
I, J, nd, ns, L, arg, it, ib: integer;
a, b, t : double;
im, rl : double;
begin
nd := length div 2; // データ数の1/2
ns := nd; // 2進数の最上位値
while ns > 0 do begin // 2進数の最上位の値が0になるまで繰り返し
L := 0; // L=0
while L < length do begin // Lの値をlengthまで、
arg := m[L] div 2; // 回転子=前の回転子の値/2 m[0]は常に0
for it := L to L + ns - 1 do begin // itの値をLの値からL+2進数の最上位の値まで繰り返し
ib := it + ns; // ib＝it + 2進数の最上位の値
if arg = 0 then begin
a := a_rl[ib];
b := a_im[ib];
end
else begin
a := a_rl[ib] * cos_tbl[arg] - a_im[ib] * sin_tbl[arg];
b := a_im[ib] * cos_tbl[arg] + a_rl[ib] * sin_tbl[arg];
end;
a_rl[ib] := a_rl[it] - a;
a_im[ib] := a_im[it] - b;
a_rl[it] := a_rl[it] + a;
a_im[it] := a_im[it] + b;
m[it] := arg; // m[it]に回転子を保存
m[ib] := arg + nd; // m[ib]に回転子 + データ数の1/2を保存
inc(loop);
end;
L := L + ns + ns; // Lの値を0からnまで、2×最上位の値のstepで繰り返し
end;
ns := ns div 2; // 2進数の最上位の値を繰り下げ
end;
for I := 0 to length - 1 do begin // データーの並べ替えビット反転処理
if I < m[I] then begin
J := m[I];
a := a_rl[I];
a_rl[I] := a_rl[J];
a_rl[J] := a;
b := a_im[I];
a_im[I] := a_im[J];
a_im[J] := b;
end;
end;
if inv = 0 then begin // invが0だったら周波数変換 データー数で除算
t := 1 / NFF; // ０データーを追加した場合追加前のデーター数で除算
for I := 0 to length - 1 do begin
a_rl[I] := a_rl[I] * t;
a_im[I] := a_im[I] * t;
end;
end;
end;
// ------------------------No3 FFT計算 ------------------------------
// a_rl: データ実数部（入出力兼用）
// a_im: データ虚数部（入出力兼用）
// length: データー個数
// inv: 変換フラグ 0 変換 1 逆変換
// 2048 で 0,18msec
// -----------------------------------------------------------------
procedure TFourierF.fft3(length, ex, inv: integer; var a_rl, a_im, sin_tbl, cos_tbl: array of double);
var
a, b: double;
g, h, i, j, k, l , o, p, q: integer;
kf, jf : double;
begin
l := length;
h := 1; // 2^0
for g := 1 to ex do begin
l := l div 2; // l 数の1/2
k := 0;
for q := 1 to h do begin
p := 0; // 回転子
for i := k to l + k -1 do begin
j := i + l;
a := a_rl[i] - a_rl[j];
b := a_im[i] - a_im[j];
a_rl[i] := a_rl[i] + a_rl[j];
a_im[i] := a_im[i] + a_im[j];
if p = 0 then begin // 回転子ゼロ時は演算の必要なし cos=1 sin=0
a_rl[j] := a;
a_im[j] := b;
end
else begin
a_rl[j] := a * cos_tbl[p] + b * sin_tbl[p];
a_im[j] := b * cos_tbl[p] - a * sin_tbl[p];
end;
p := p + h; // 回転子+h
inc(loop);
end;
k := k + l + l; // K + 2l
end;
h := h + h; // 2~n 2, 4, 8 ....
end;
j := length div 2;
for i := 1 to length -1 do begin // ピッ演算子による並び替え
k := length;
if j < i then begin
a := a_rl[i];
a_rl[i] := a_rl[j];
a_rl[j] := a;
b := a_im[i];
a_im[i] := a_im[j];
a_im[j] := b;
end;
k := k shr 1; // k = k div 2
while j >= k do begin
j := j - k;
k := k shr 1; // k = k div 2
if k = 0 then break;
end;
j := j + k;
end;
if inv = 0 then begin // invが0だったら周波数変換 データー数で除算
a := 1 / NFF; // ０データーを追加した場合追加前のデーター数で除算
for I := 0 to length - 1 do begin
a_rl[I] := a_rl[I] * a;
a_im[I] := a_im[I] * a;
end;
end;
end;
//--------------------------- No4 ---------------------------
// fftcmp2の複素数を実数、虚数形式に変換
// n データー数
// xr, xi データー 実数部 虚数部
// sin_tbl cos_tbl sin cos テーブル
//-----------------------------------------------------------
procedure TFourierF.fft4(n: integer; var xr, xi, sin_tbl, cos_tbl: array of double);
var
a, b: double;
i, ia, ib, j, k, ns, arg : integer;
begin
ns := n div 2;
while ns >= 1 do begin
arg := 0;
j := 0;
while j < n do begin
k := n shr 2; // k = n / 4
for ia := j to j + ns - 1 do begin
ib := ia + ns;
if arg = 0 then begin
a := xr[ib];
b := xi[ib];
end
else begin
a := xr[ib] * cos_tbl[arg] - xi[ib] * sin_tbl[arg];
b := xr[ib] * sin_tbl[arg] + xi[ib] * cos_tbl[arg];
end;
xr[ib] := xr[ia] - a;
xi[ib] := xi[ia] - b;
xr[ia] := xr[ia] + a;
xi[ia] := xi[ia] + b;
inc(loop);
end;
while k <= arg do begin // ループ数多
arg := arg - k;
k := k shr 1; // k = k / 2
if k = 0 then break;
end;
arg := arg + k;
j := j + ns + ns;
end;
ns := ns shr 1; // ns = ns / 2
end;
a := 1 / NFF;
for i := 0 to n - 1 do begin
xr[i] := xr[i] * a;
xi[i] := xi[i] * a;
end;
j := 1; // ビット反転処理
for i := 1 to n - 1 do begin
if i <= j then begin
a := xr[i - 1];
b := xi[i - 1];
xr[i - 1] := xr[j - 1];
xi[i - 1] := xi[j - 1];
xr[j - 1] := a;
xi[j - 1] := b;
end;
k := n shr 1; // k = n / 2
while k < j do begin
j := j - k;
k := k shr 1; // k = k / 2
end;
j := j + k;
end;
end;
// ------------------------No5 FFT計算 ------------------------------
// n データー個数
// xr: データ実数部（入出力兼用）
// xi: データ虚数部（入出力兼用）
// -----------------------------------------------------------------
procedure TFourierF.fftNo5(n, ex: integer; var xr, xi, sin_tbl, cos_tbl: array of double);
var
i, j, k, m, j1, j2, dn, w, arg: integer;
t1, t2: double;
begin
dn := n;
w := 1;
for i := 1 to ex do begin
m := dn;
dn := dn div 2;
arg := 0;
for j := 0 to dn - 1 do begin
k := m;
while k <= n do begin
j1 := k - m + j;
j2 := j1 + dn;
t1 := xr[j1] - xr[j2];
t2 := xi[j1] - xi[j2];
xr[j1] := xr[j1] + xr[j2];
xi[j1] := xi[j1] + xi[j2];
if arg = 0 then begin
xr[j2] := t1;
xi[j2] := t2;
end
else begin
xr[j2] := t1 * cos_tbl[arg] + t2 * sin_tbl[arg];
xi[j2] := t2 * cos_tbl[arg] - t1 * sin_tbl[arg];
end;
k := k + m;
inc(loop);
end;
arg := arg + w;
end;
w := w shl 1; // w = w * 2
end;
j := 1;
dn := n div 2;
for i := 1 to n - 1 do begin // ビット反転処理
if i < j then begin
j1 := i - 1;
j2 := j - 1;
t1 := xr[j2];
t2 := xi[j2];
xr[j2] := xr[j1];
xi[j2] := xi[j1];
xr[j1] := t1;
xi[j1] := t2;
end;
k := dn;
while k < j do begin
j := j - k;
k := k shr 1; // k = k / 2
end;
j := j + k;
end;
t1 := 1 / NFF;
for i := 0 to n - 1 do begin
xr[i] := xr[i] * t1;
xi[i] := xi[i] * t1;
end;
end;
// ----------------------- フーリエ変換 ---------------------------------
// Checkbox1でFFTとDFT計算選択。
// Checkbox2でFFT計算時のデーター数が2^nになっていない場合の処理選択
// Checkbox3でFFT計算ルーチンの選択
// FFT inv 0 で周波数変換 0以外で逆変換 ここでは0周波数変換のみ使用します。
// 逆変換時は 配列anに実数側 配列bnに虚数側データーのセットが必要です。
// DFTには逆変換なし。
// dft fft は平均値と最大周波数(データー数の1/2)の値を除き1/2の値になります。
procedure TFourierF.FourierCalc; //フーリエ変換
var
{
// グローバル変数に割り当てた方が速度が安定します
Xindat: array of Double; // 入力データ
an: array of Double; // con変換 実数部
bn: array of Double; // sin変換 虚数部
Fv: array of Double; // リニアレベル
Qf: array of Double; // 位相角
dpic: array of Double; // cos(2pi / N J)
dpis: array of Double; // sin(2pi / N J)
buf_x: array of Double; // 作業用バッファ
m : array of integer; // bit反転処理用
x: array of Tcmplx; // 複素数
}
pi2n: double; // 2*π/N
az: double; // an合計
bz: double; // bn合計
II,JJ,KK: integer;
X_EXP: integer; // 2^X_EXP
inv: integer; // 0 周波数変換 1 逆変換
kv: double; // リアル出力補正倍数 2
wink: double;
begin
// FFT & カイザー窓関数だったら
if CheckBox1.Checked then begin
if RadioGroup2.ItemIndex = Kaiser then begin
val(KaiserEdit.Text, ka, II);
if II <> 0 then begin
MessageDlg('カイザーα値に入力値に誤りが有ります', mtInformation,[mbOk], 0);
exit;
end;
end;
end;
bitbtn2.Enabled := False;
bitbtn3.Enabled := False;
BitBtn5.Enabled := False;
BitBtn6.Enabled := False;
BitBtn7.Enabled := False;
loop := 0;
inv := 0; // 0 周波数変換 此処では逆変換は使用しません
kv := 1;
if checkbox4.Checked then kv := 2; // dft fftの性質でリアル値が1/2になるので補正値
SetLength(Xindat, N); // 入力データー配列確保
SetLength(BXindat, N); // 入力データー配列確保
// グリッドセルデーターから配列データーの作成
for II := 0 to N - 1 do
// 数値入力か確認変換します 数値でなかったら中止
if not incheck(StringGrid1.Cells[1, II + 1], Xindat[II]) then begin
MessageDlg('Ｎｏ' + intTostr(II + 1) + ' に入力値に誤りが有ります', mtInformation,[mbOk], 0);
exit;
end;
// DFT FFT選択
if CheckBox1.Checked then begin
// ------------- FFT --------------------------------
// カイザー窓関数補正係数
if RadioGroup2.ItemIndex = Kaiser then begin
if ka < 1 then
akv :=-0.35043706 * ka * ka * ka * Ka + 1.0925932 * ka * ka * ka - 1.0941098 * ka * ka
+ 0.023141084 * Ka + 0.9998586;
if (ka >= 1) and (ka < 2) then
akv := 0.08042 * ka * ka - 0.42315 * ka + 1.01378;
if ka >= 2 then
akv := 0.689064231298894 * power(ka, -0.490866859636135);
akv := 1 / akv;
end;
// データー数2のn乗確認
X_EXP := 0;
II := 1;
repeat
II := II * 2;
inc(X_EXP);
until N <= II;
// データー数が2^nに成っていない場合の調整
if (checkBox2.Checked) and (N <> II) then begin // 2^nにデーター数カット
NF := II div 2;
NFF := NF;
dec(X_EXP);
SetLength(Xindat, NF); // 入力データー配列確保
SetLength(BXindat, NF);
end
else begin // 2^nにデーター数アップ
if N <> II then
application.MessageBox('データーが2のn乗個になっていません。','注意',0);
NF := II;
NFF := N;
end;
// 窓関数の設定
case RadioGroup2.ItemIndex of
Hanning : WinHanning(Xindat);
Hamming : WinHamming(Xindat);
Gauss : WinGauss(Xindat, 1); // 1, 2, 3 シグマ(σ)
BlackmanHarris : WinBlackmanHarris(Xindat);
BlackmanNuttall : WinBlackmanNuttall(Xindat);
FlapTop : WinFlapTop(Xindat);
HalfSin : WinHalfSin(Xindat);
Kaiser : WinKaiser(ka, Xindat);
end;
// 表示用データーの保存
for II := 0 to length(Xindat) - 1 do BXindat[II] := Xindat[II];
// 窓関数係数
wink := 1;
if checkbox3.Checked = true then begin
case RadioGroup2.ItemIndex of
Hanning : wink := han; // han = 1 / 0.5;
Hamming : wink := ham; // ham = 1 / 0.53997;
Gauss : wink := gus; // gus = 1 / 0.85561;
BlackmanHarris : wink := har; // har = 1 / 0.35873;
BlackmanNuttall : wink := nut; // nut = 1 / 0.36356;
FlapTop : Wink := fla; // fla = 1 / 0.9994;
HalfSin : Wink := hal; // hal = 1 / 0.63658;
Kaiser : WinK := akv;
end;
for II := 0 to length(Xindat) - 1 do Xindat[II] := Xindat[II] * Wink;
end;
TF := T / N * NF;; // サンプリング時間をデーター数で補正
StringGrid2Set; // 計算結果のグリッド設定
// 配列の確保
if RadioGroup1.ItemIndex = No1 then SetLength(buf_x, NF); // データーの並べ替えビット反転処理用バッファ
if RadioGroup1.ItemIndex = No2 then SetLength(m, NF); // データーの並べ替えビット反転処理用ビット配列
if RadioGroup1.ItemIndex = comp1 then begin
SetLength(x, NF); // データー用複素数配列
end
else begin
SetLength(an, NF);
SetLength(bn, NF);
SetLength(dpic, NF);
SetLength(dpis, NF);
end;
if RadioGroup1.ItemIndex = comp2 then SetLength(x, NF) // データー用複素数配列
else begin
SetLength(an, NF);
SetLength(bn, NF);
end;
SetLength(FV, NF div 2 + 1);
SetLength(Qf, NF div 2 + 1);
// Sin,Cos 配列テーブル作成
pi2n := pi * 2 / NF; // 計算回転ピッチ角 周波数変換なので-Π 逆変換時は＋Π
if inv = 0 then pi2n := - pi2n; // 周波数変換なら符号反転
// 計算速度UPの為 Sin,Cos 配列テーブル作成
if RadioGroup1.ItemIndex <> comp1 then
for II := 0 To NF - 1 do begin
dpic[II] := cos(pi2n * II); // cos用配列作成
dpis[II] := sin(pi2n * II); // sin用配列作成
end;
// 入力データーの配列へのセット
if (RadioGroup1.ItemIndex = comp1) or (RadioGroup1.ItemIndex = comp2) then begin
if checkBox2.Checked then
for II := 0 to NF - 1 do begin // 2^nにデーターをカットした場合2^n分だけ
x[II].real := Xindat[II]; // 実数側に入力データーセット
x[II].Imaginary := 0;
end
else
for II := 0 to N - 1 do begin // カットしない場合全データーセット
x[II].real := Xindat[II]; // 実数側に入力データーセット
x[II].Imaginary := 0;
end;
end
else begin
if checkBox2.Checked then
for II := 0 to NF - 1 do // 2^nにデーターをカットした場合2^n分だけ
an[II] := Xindat[II] // 実数側に入力データーセット
else
for II := 0 to N - 1 do // カットしない場合全データーセット
an[II] := Xindat[II]; // 実数側に入力データーセット
end;
Start;
if checkbox1.Checked then begin
case RadioGroup1.ItemIndex of
No3 : fft3(NF, X_EXP, inv, an, bn, dpis, dpic);
No2 : fft2(NF, inv, an, bn, dpis, dpic, m);
No1 : fft1core(NF, X_EXP, inv, an, bn, dpis, dpic, buf_x);
comp1 : fftcmp(NF, x);
comp2 : fftcmp2(NF, x, dpis, dpic);
No4 : fft4(NF, an, bn, dpis, dpic);
No5 : fftNo5(NF, X_EXP, an, bn, dpis, dpic);
end;
end;
stwT := Stop;
memo1.Lines.Add('interval');
memo1.Lines.Add(' ' + floatTostr(stwT) + 'msec');
end
else begin
// -------------- DFT --------------------------------
NF := N;
SetLength(dpic, NF);
SetLength(dpis, NF);
SetLength(an, NF);
SetLength(bn, NF);
SetLength(FV, NF div 2 + 1);
SetLength(Qf, NF div 2 + 1);
TF := T;
StringGrid2Set; // 計算結果のグリッド設定
// 計算速度UPの為 Sin,Cos 配列テーブル作成
pi2n := - pi * 2 / NF; // 計算ピッチ角 周波数変換なので-Π 逆変換時は＋Π
for II := 0 To NF - 1 do begin
dpic[II] := cos(pi2n * II); // cos用配列作成
dpis[II] := sin(pi2n * II); // sin用配列作成
end;
// 表示用データーの保存
for II := 0 to length(Xindat) - 1 do BXindat[II] := Xindat[II];
Start;
// 変換ルーチン2048 で 13msec
for JJ := 0 to NF div 2 do begin
az := 0;
bz := 0;
for II := 0 to NF - 1 do begin // Σ計算
KK := II * JJ mod NF; // N J
az := az + Xindat[II] * dpic[KK]; // Σcos計算
bz := bz + Xindat[II] * dpis[KK]; // Σsin計算
inc(loop);
end;
az := az / NF; // an 計算結果
bz := bz / NF; // bn 計算結果
an[JJ] := az;
bn[JJ] := bz;
end;
stwT := Stop;
memo1.Lines.Add('interval');
memo1.Lines.Add(' ' + floatTostr(stwT) + 'msec');
end;
memo1.Lines.Add('Loop ' + intTostr(loop));
// ----------------------------------------------------
if inv = 0 then begin // 周波数変換だったらリニア値 位相角計算
if CheckBox1.Checked and ((RadioGroup1.ItemIndex = comp1) or (RadioGroup1.ItemIndex = comp2)) then begin
FV[0] := x[0].real * kv; // 平均値
Qf[0] := arctan2(x[0].Imaginary, x[0].real) / pi * 180; // 位相角
end
else begin
FV[0] := an[0] * kv; // 平均値
Qf[0] := arctan2(bn[0], an[0]) / pi * 180; // 位相角
end;
if CheckBox1.Checked and ((RadioGroup1.ItemIndex = comp1) or (RadioGroup1.ItemIndex = comp2)) then begin
for JJ := 1 to NF div 2 do begin
FV[JJ] := sqrt(sqr(x[JJ].real) + sqr(x[JJ].Imaginary)) * kv; // リニア値 最後の値 FV = √(az^2 + bz^2)
Qf[JJ] := arctan2(x[JJ].Imaginary, x[JJ].real) / pi * 180; // 位相角
end;
end
else begin
for JJ := 1 to NF div 2 do begin
FV[JJ] := sqrt(sqr(an[JJ]) + sqr(bn[JJ])) * kv; // リニア値 最後の値 FV = √(az^2 + bz^2)
Qf[JJ] := arctan2(bn[JJ], an[JJ]) / pi * 180; // 位相角
end;
end;
end;
// グリッドセルにに計算結果表示
for JJ := 0 to NF div 2 do begin
StringGrid2.Cells[0, JJ + 1] := floatTostrF(JJ / TF, ffGeneral,5,2);
if CheckBox1.Checked and ((RadioGroup1.ItemIndex = comp1) or (RadioGroup1.ItemIndex = comp2)) then begin
StringGrid2.Cells[1, JJ + 1] := floatTostrF(x[JJ].real,ffGeneral,5,2);
StringGrid2.Cells[2, JJ + 1] := floatTostrF(x[JJ].Imaginary,ffGeneral,5,2);
end
else begin
StringGrid2.Cells[1, JJ + 1] := floatTostrF(an[JJ],ffGeneral,5,2);
StringGrid2.Cells[2, JJ + 1] := floatTostrF(bn[JJ],ffGeneral,5,2);
end;
StringGrid2.Cells[3, JJ + 1] := floatTostrF(FV[JJ],ffGeneral,5,2);
StringGrid2.Cells[4, JJ + 1] := floatTostrF(Qf[JJ],ffGeneral,5,2);
end;
Calcd := True;
bitbtn2.Enabled := True;
bitbtn3.Enabled := True;
BitBtn5.Enabled := True;
BitBtn6.Enabled := True;
BitBtn7.Enabled := True;
// 配列グローバル変数の時は配列開法 ローカルの時は必要なし
Finalize(Xindat); // 入力データ
Finalize(an); // con変換 実数部
Finalize(bn); // sin変換 虚数部
Finalize(Fv); // リニアレベル
Finalize(Qf); // 位相角
Finalize(dpic); // cos(2pi / N J)
Finalize(dpis); // sin(2pi / N J)
Finalize(buf_x); // 作業用バッファ
Finalize(m); // bit反転処理用
Finalize(x); // 複素数
end;
//-----------------------------------------------------------------------------------------------
// データー数入力値の確認
function TFourierF.Edit1Check:integer; // Edit1入力チェック
var
check: integer;
begin
val(Edit1.Text, Result, check);
if check <> 0 then result := 0;
end;
// サンプリング時間入力値の確認
// val関数を使用した方が簡単
function TFourierF.Edit2Check:integer; // Edit2入力チェック
var
inch: char;
instring: string;
dotcheck,II,Sleng: integer;
begin
instring := Edit2.Text;
Sleng := Length(instring);
Result := 0;
if Sleng = 0 then exit;
dotcheck := 0;
for II := 1 to Sleng do begin
inch := instring[II];
case inch of
'.': inc(dotcheck);
end;
end;
Result := dotcheck;
if dotcheck <= 1 then T := strToFloat(instring)
else T := 0;
end;
// サンプル数の変更が有ったら計算未実行に
procedure TFourierF.Edit1Change(Sender: TObject);
begin
Calcd := False;
end;
// サンプル数入力数値キーか確認
// 数字入力のみにします
procedure TFourierF.Edit1KeyPress(Sender: TObject; var Key: Char);
begin
case key of
'0'..'9':;
#8:;
else key := #0;
end;
end;
// サンプリング時間が変更されたら計算未実行に
procedure TFourierF.Edit2Change(Sender: TObject);
begin
Calcd := False;
end;
// サンプリング時間入力数値キーか確認
// 数字入力のみにします
procedure TFourierF.Edit2KeyPress(Sender: TObject; var Key: Char);
begin
case key of
'0'..'9':;
#8:;
'.':;
else key := #0;
end;
end;
// データーチェック
// 数値でなかったらFalse
function TFourierF.incheck(Indat: string; var data: double): Boolean; // 入力チェック
var
Check : Integer;
begin
Result := False;
val(Indat, data, check);
if check <> 0 then exit;
Result := True;
end;
// ストリンググリッドの入力キー確認
// 数字入力のみ有効にします
procedure TFourierF.StringGrid1KeyPress(Sender: TObject; var Key: Char);
begin
case Key of
'0'..'9':;
#8:;
'.':;
' ':;
'-':;
'E':;
'e':;
else key := #0;
end;
Calcd := False;
end;
//------------------ 計算画面のの表示設定 ------------------
// 計算結果用ステリンググリッド表示設定
procedure TFourierF.StringGrid2Set;
var
II : integer;
begin
with StringGrid2 do begin
Options := [goFixedVertLine,goFixedHorzLine,goVertLine,goHorzLine];
RowCount := NF div 2 + 2;
ColWidths[0] := 80;
ColWidths[1] := 95;
ColWidths[2] := 95;
ColWidths[3] := 95;
ColWidths[4] := 95;
Cells[0,0] := '周波数';
Cells[0,1] := '0';
Cells[1,0] := 'an';
Cells[2,0] := 'bn';
Cells[3,0] := 'An';
Cells[4,0] := 'φn (deg)';
if NF <= 20 then ClientHeight := (DefaultRowHeight + 1) * (NF div 2 + 2)
else ClientHeight := (DefaultRowHeight + 1) * (10 + 2);
for II := 1 to NF div 2 do Cells[0,II + 1] := floatTostrF(II / T ,ffFixed,6,2);
ClientWidth := ColWidths[0] + ColWidths[1] * 4 + ColCount;
end;
end;
// 計算用画面設定
// 入力データー編集用グリッド 計算結果用グリッド表示
// 計算用ボタン類表示設定
procedure TFourierF.Ddisp;
var
II,KK : integer;
begin
Label1.Visible := False;
Label2.Visible := False;
Label3.Visible := False;
edit1.Visible := False;
edit2.Visible := False;
KaiserEdit.Visible := True;
BitBtn1.Visible := False;
BitBtn4.Visible := False;
StringGrid1.Visible := True;
StringGrid2.Visible := True;
BitBtn2.Visible := True;
BitBtn3.Visible := True;
BitBtn5.Visible := True;
BitBtn6.Visible := True;
BitBtn7.Visible := True;
CheckBox1.Visible := True;
CheckBox2.Visible := True;
CheckBox3.Visible := True;
CheckBox4.Visible := True;
CheckBox2.Enabled := False;
RadioGroup1.Visible := True;
RadioGroup2.Visible := True;
memo1.Visible := True;;
CheckBox2.Caption := '2' + #$207F + 'にData Cut';
// データー数が2^nか確認 2^nで無かったらFFT 2^nデーターカットチェックボックイネーブル
II := 1;
repeat
II := II * 2;
until N <= II;
if N <> II then begin
CheckBox2.Enabled := True;;
end;
ClientWidth := 815;
ClientHeight := 500;
StringGrid1.SetFocus;
StringGrid2Set; // 計算結果表示グリッド設定
// 入力データーストリンググリッド表示設定
with StringGrid1 do begin
RowCount := N + 1;
ColWidths[1] := 190;
Cells[0,0] := 'No';
Cells[1,0] := 'Data';
if N <= 10 then ClientHeight := (DefaultRowHeight + 1) * (N + 1)
else ClientHeight := (DefaultRowHeight + 1) * (10 + 1);
ClientWidth := ColWidths[0] + ColWidths[1] + ColCount;
for II := 1 to N do Cells[0,II] := intTostr(II);
end;
Top := (Screen.height - Height) div 2;
Left := (Screen.Width - Width) div 2;
// 未計算の場合計算結果欄を消去
if not calcd then for II := 1 to 4 do
for KK := 1 to N + 1 do StringGrid2.Cells[II, KK] := '';
end;
// 計算結果表示グリッドの固定セル表示設定
procedure TFourierF.StringGrid2DrawCell(Sender: TObject; ACol,
ARow: Integer; Rect: TRect; State: TGridDrawState);
begin
with StringGrid2.Canvas do begin
Font := StringGrid2.Font;
// 固定セルの色指定
if gdFixed in State then Brush.Color := StringGrid2.FixedColor
else if (gdFocused in state) or (state = []) then Brush.Color := StringGrid2.Color // セル色指定
else Brush.Color := StringGrid2.Color; // 選択セルの色
// テキストの表示
TextRect(Rect, Rect.Left + 2, Rect.Top + 2, StringGrid2.Cells[ACol, ARow]);
end;
end;
// 入力データーグリッドの固定セル表示設定
procedure TFourierF.StringGrid1DrawCell(Sender: TObject; ACol,
ARow: Integer; Rect: TRect; State: TGridDrawState);
begin
with StringGrid1.Canvas do begin
Font := StringGrid1.Font;
// 固定セルの色指定
if gdFixed in State then
Brush.Color := StringGrid1.FixedColor
else
// セル色指定
if (gdFocused in state) or (state = []) then
Brush.Color := StringGrid1.Color
else begin
// 選択セルの色
Brush.Color := StringGrid1.Color;
end;
// テキストの表示部
TextRect(Rect, Rect.Left + 2, Rect.Top + 2, StringGrid1.Cells[ACol, ARow]);
end;
end;
//---------- データー数 サンプリング時間 ファイル入力画面設定 --------------------
procedure TFourierF.Ndisp;
begin
Label1.Visible := True;
Label2.Visible := True;
Label3.Visible := True;
edit1.Visible := True;
edit2.Visible := True;
KaiserEdit.Visible := False;
BitBtn1.Visible := True;
BitBtn4.Visible := True;
StringGrid1.Visible := False;
StringGrid2.Visible := False;
BitBtn2.Visible := False;
BitBtn3.Visible := False;
BitBtn5.Visible := False;
BitBtn6.Visible := False;
BitBtn7.Visible := False;
CheckBox1.Visible := False;
CheckBox2.Visible := False;
CheckBox3.Visible := False;
CheckBox4.Visible := False;
RadioGroup1.Visible := False;
RadioGroup2.Visible := False;
memo1.Visible := False;
ClientWidth := 455;
ClientHeight := 150;
Left := (Screen.Width - Width) div 2;
Top := (Screen.Height - Height) div 2;
end;
//--------- データー数 サンプリング時間 ファイル入力画面から 計算画面への移動設定 -----
// 入力ミスの確認も実行
procedure TFourierF.BitBtn1Click(Sender: TObject);
//var
// Menus: HMENU;
begin
if Length(Edit1.Text) > 0 then N := Edit1Check
else begin
MessageDlg('データー数が' + #13#10 + '入力されていません', mtInformation,[mbOk], 0);
exit;
end;
if N < 2 then begin
MessageDlg('データーの数が' + #13#10 + '少なすぎます。', mtInformation,[mbOk], 0);
exit;
end;
// if N mod 2 > 0 then begin
// MessageDlg('データーの数を偶数にして下さい。', mtInformation,[mbOk], 0);
// exit;
// end;
if Length(Edit2.Text) = 0 then begin
MessageDlg('サンプリング時間が' + #13#10 + '入力されていません', mtInformation,[mbOk], 0);
exit;
end;
if Edit2Check > 1 then begin
MessageDlg('サンプリング時間の' + #13#10 + '小数点の数が多すぎます。', mtInformation,[mbOk], 0);
exit;
end;
if T <= 0 then begin
MessageDlg('サンプリング時間は' + #13#10 + 'ゼロ以上にしてください。', mtInformation,[mbOk], 0);
exit;
end;
BitBtn6.Enabled := False;
BitBtn7.Enabled := False;
NF := N;
Ddisp; //データー入力 及び 計算
// Menus := GetSystemMenu(Handle,false);
// EnableMenuItem(Menus,SC_CLOSE,MF_BYCOMMAND or MF_GRAYED);
// DrawMenuBar(Handle);
end;
//-------------- フーリエ変換開始 --------------------
// グリッドの入力データーチェック後に計算
procedure TFourierF.BitBtn2Click(Sender: TObject);
var
II: integer;
begin
Memo1.clear;
for II:= 1 to N do
// 入力の全く無い入力データーセルはゼロに設定します
if StringGrid1.Cells[1,II] = '' then StringGrid1.Cells[1,II] := '0';
// 現在の時刻を取得しておく
FourierCalc; // フーリエ変換
end;
//-------- サンプリング時間 データー数 ファイル読み込み画面表示 ----------
procedure TFourierF.BitBtn3Click(Sender: TObject);
//var
// Menus: HMENU;
begin
Ndisp; //データー数入力画面設定
// Menus := GetSystemMenu(Handle,false);
// EnableMenuItem(Menus,SC_CLOSE,MF_BYCOMMAND or MF_ENABLED);
// DrawMenuBar(Handle);
end;
//------------ ファイルからのデーター読み込み --------------------
procedure TFourierF.BitBtn4Click(Sender: TObject);
var
KK,II: integer;
ind : double;
begin
if OpenDialog1.Execute then begin
Calcd := False; // 計算済みフラグリセット
try
AssignFile(F1,OpenDialog1.FileName);
Reset(F1);
Readln(F1,N,T); // データー数N サンプリング時間T
Edit1.Text := intTostr(N);
Edit2.Text := floatTostr(T);
for KK := 1 to N do begin // データーN個読み込み
Readln(F1,ind);
StringGrid1.Cells[1,KK] := FloatTostr(ind); // ストリンググリッドに追加
end;
finally
CloseFile(F1);
end; // 計算結果消去
for II := 1 to 4 do for KK := 1 to N + 1 do StringGrid2.Cells[II, KK] := '';
end;
end;
//------------- 入力データーの保存 -------------------------------
procedure TFourierF.BitBtn5Click(Sender: TObject);
var
KK: integer;
begin
SaveDialog1.Options := [ofHideReadOnly,ofNoReadOnlyReturn];
if SaveDialog1.Execute then
begin
if AnsiLowerCase(ExtractFileExt(SaveDialog1.FileName)) <> '.fre' then
SaveDialog1.FileName := SaveDialog1.FileName + '.fre';
if FileExists(SaveDialog1.FileName) then begin
if MessageDlg('既にファイルが存在します 上書きしますか',mtConfirmation,
[mbYes, mbNo], 0) = mrNo then exit;
end;
try
AssignFile(F1, SaveDialog1.FileName);
ReWrite(F1); // ファイル先頭にセット
Writeln(F1,N,T); // データー数 サンプリング時間 書き出し
for KK := 1 to N do Writeln(F1,StringGrid1.Cells[1,KK]); // データー書き出し
finally
CloseFile(F1);
end;
end;
end;
//----------------- リニアグラフ表示実行 ----------
procedure TFourierF.BitBtn6Click(Sender: TObject);
begin
if not Calcd then begin
MessageDlg('計算を実行して下さい。', mtInformation,[mbOk], 0);
exit;
end;
GraphF.Chart1.Title.Text.Clear;
if CheckBox1.Checked then GraphF.Chart1.Title.Text.Add('FFT リニア')
else GraphF.Chart1.Title.Text.Add('DFT リニア');
GraphF.Show; // グラフフォーム表示
Hide; // 計算フォーム非表示
DispF := True; // 周波数リニアグラフ表示フラグ
GraphF.Chart2.Visible := False; // データーグラフ非表示
GraphF.Chart1.Visible := True;; // 周波数リニアグラフ表示
GraphF.Linear; // 周波数リニアグラフ描画
end;
//--------------------- 計算結果保存 sub -------------
procedure TFourierF.CalcSave;
var
II,JJ: integer;
begin
Writeln(F2,'周波数',',','an',',','bn',',','An',',','φ');
for II := 1 to NF div 2 + 1 do
begin // 計算結果書き出し
for JJ := 0 to 3 do Write(F2,StringGrid2.Cells[JJ,II],',');
Writeln(F2,StringGrid2.Cells[4,II]);
end;
end;
procedure TFourierF.CheckBox1MouseUp(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y: Integer);
begin
if CheckBox1.Checked = true then RadioGroup1.Enabled := true
else RadioGroup1.Enabled := False;
if CheckBox1.Checked = true then RadioGroup2.Enabled := true
else RadioGroup2.Enabled := False;
end;
//------------------- 計算結果の保存 -------------
// csv形式の保存
procedure TFourierF.BitBtn7Click(Sender: TObject);
begin
if not Calcd then begin
MessageDlg('計算を実行して下さい。', mtInformation,[mbOk], 0);
exit;
end;
SaveDialog2.Options := [ofHideReadOnly,ofNoReadOnlyReturn];
if SaveDialog2.Execute then begin
if AnsiLowerCase(ExtractFileExt(SaveDialog2.FileName)) <> '.csv' then
SaveDialog2.FileName := SaveDialog2.FileName + '.csv';
if FileExists(SaveDialog2.FileName) then begin
if MessageDlg('既にファイルが存在します 上書きしますか',mtConfirmation,
[mbYes, mbNo], 0) = mrNo then exit;
end;
try
AssignFile(F2, SaveDialog2.FileName);
ReWrite(F2); // ファイル先頭にセット
CalcSave; // 計算結果書き込み
finally
CloseFile(F2);
end;
end;
end;
// ------------- 初期設定 ---------------------------
procedure TFourierF.FormCreate(Sender: TObject);
begin
FourierF.BorderIcons := [bisystemMenu, biMinimize];
Edit1.Text := '';
Edit2.Text := '';
with Label1 do begin Left := 48; top := 16; Width := 80; Height := 14; Font.Height := 14; end;
with Label2 do begin Left := 48; top := 56; Width := 80; Height := 14; Font.Height := 14; end;
with Label3 do begin Left := 20; top := 96; Width := 410; Height := 14; Font.Height := 12; end;
with Edit1 do begin Left := 136; top := 12; width := 80; Height := 20; Font.Height := 15; end;
with Edit2 do begin Left := 136; top := 52; width := 80; Height := 20; Font.Height := 15; end;
with KaiserEdit do begin Left := 440; top :=450; width := 73; Height := 20; Font.Height := 12; end;
with BitBtn1 do begin Left := 264; Top := 48; width := 65; Height := 25; Font.Height := 16; end;
with BitBtn4 do begin Left := 370; Top := 48; width := 70; Height := 25; Font.Height := 16; end;
with StringGrid1 do begin Left := 30; Top := 16; width := 134; Height := 280; Font.Height := 15; end;
with StringGrid2 do begin Left := 320; Top := 16; width := 134; Height := 280; Font.Height := 15; end;
With BitBtn2 do begin Left := 10; Top := 330; width := 80; Height := 35; Font.Height := 15;
caption := '入力終了' + #13#10 + '計算'; end;
With CheckBox1 do begin Left := 100; Top := 320; width := 80; Height := 18; Font.Height := 15; end;
With CheckBox2 do begin Left := 100; Top := 350; width := 120; Height := 18; Font.Height := 15; end;
With CheckBox3 do begin Left := 440; Top := 400; width := 200; Height := 18; Font.Height := 15; end;
With CheckBox4 do begin Left := 100; Top := 380; width := 120; Height := 18; Font.Height := 15; end;
With BitBtn3 do begin Left := 20; Top := 400; width := 73; Height := 25; Font.Height := 15; end;
With BitBtn6 do begin Left := 435; Top := 340; width := 73; Height := 25; Font.Height := 15; end;
With BitBtn5 do begin Left := 520; Top := 340; width := 73; Height := 25; Font.Height := 15; end;
With BitBtn7 do begin Left := 600; Top := 340; width := 73; Height := 35; Font.Height := 12;
caption := '計算結果' + #13#10 + 'Save'; end;
With memo1 do begin Left := 685; top := 335; width := 117; height := 70; end;
With RadioGroup1 do begin
Items.Add('No1');
Items.Add('No2');
Items.Add('No3');
Items.Add('comp1');
Items.Add('comp2');
Items.Add('No4');
Items.Add('No5');
left := 208; top := 327; height := 155; width := 65;
RadioGroup1.Enabled := false;
end;
RadioGroup1.ItemIndex := 0;
With RadioGroup2 do begin
Items.Add('窓関数なし');
Items.Add('ハン');
Items.Add('ハミング');
Items.Add('ガウス');
Items.Add('ブラックマンハリス');
Items.Add('ブラックマンナットール');
Items.Add('フラップトップ');
Items.Add('半正弦波');
Items.Add('カイザー');
left := 280; top := 327; height := 155; width := 145;
RadioGroup2.Enabled := false;
end;
RadioGroup2.ItemIndex := 0;
memo1.Clear;
CheckBox3.Checked := True;
CheckBox4.Checked := True;
Label3.Caption := 'データーの数は、偶数にして下さい、周波数はデーターの数の１／２迄計算されます。' + #13#10 +
'サンプリング時間は、データーを測定した時間で単位は、秒(sec)です。' + #13#10 +
'* FFTを使用する場合は、データー数を２の累乗個にすると精度が高くなります。';
Ndisp; // データー数 サンプリング時間 ファイル入力画面設定
end;
end.
unit graph;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, ExtCtrls, StdCtrls, Buttons, VclTee.TeeGDIPlus, VCLTee.TeEngine, VCLTee.Series,
VCLTee.TeeProcs, VCLTee.Chart;
type
TGraphF = class(TForm)
BitBtn1: TBitBtn;
BitBtn2: TBitBtn;
Chart1: TChart;
Series1: TBarSeries;
Chart2: TChart;
Series2: TLineSeries;
procedure FormCreate(Sender: TObject);
procedure BitBtn1Click(Sender: TObject);
procedure BitBtn2Click(Sender: TObject);
procedure FormClose(Sender: TObject; var Action: TCloseAction);
private
{ Private 宣言 }
procedure inpdata; // データーグラフ描画
protected
procedure CreateParams(var Params: TCreateParams); Override;
procedure WMSysCommand(var Message: TWMSysCommand); message WM_SYSCOMMAND;
public
{ Public 宣言 }
procedure Linear; // スケール描画
end;
var
GraphF: TGraphF;
DispF: Boolean; // グラフ表示モード
implementation
uses Fourier;
{$R *.dfm}
const
Mymenu = 100; // 追加メニューのID No
//=================================================================
// メニューを選択した時のメッセージ処理
//=================================================================
procedure TGraphF.WMSysCommand(var Message: TWMSysCommand);
begin
case Message.CmdType of
Mymenu: close;
end;
inherited;
end;
//====================================================================
// タスクバーにメインの画面でなく現在の画面を表示するようにします。
//====================================================================
procedure TGraphF.CreateParams(var Params: TCreateParams);
begin
inherited;
Params.ExStyle := Params.ExStyle or WS_EX_APPWINDOW;
Params.WndParent := Application.Handle;
end;
//==================================================================
//---------------------- データーグラフ描画 ------------------------
procedure TGraphF.inpdata;
var
dispdat : double;
II: integer;
max, min : double;
begin
max := 0;
min := 0;
Series2.Clear;
for II := 0 to NF -1 do begin
dispdat := 0;
// if II < N then
// if Fourierf.StringGrid1.Cells[1, II + 1] <> '' then
// dispdat := StrtoFloat(Fourierf.StringGrid1.Cells[1, II + 1]);
if II < N then dispdat := BXindat[II];
Series2.AddXY(II, dispdat);
if dispdat > max then max := dispdat;
if dispdat < min then min := dispdat;
end;
chart2.LeftAxis.AutomaticMaximum := False;
chart2.LeftAxis.AutomaticMinimum := False;
if chart2.LeftAxis.Minimum >= max + (max - min) / 5 then begin
chart2.LeftAxis.Minimum := min - (max - min) / 5;
chart2.LeftAxis.Maximum := max + (max - min) / 5;
end
else begin
chart2.LeftAxis.Maximum := max + (max - min) / 5;
chart2.LeftAxis.Minimum := min - (max - min) / 5;
end;
BitBtn1.Caption := '表示周波数ｸﾞﾗﾌ';
end;
//-------------- フーリエ変換結果 リニア描画 ----------------------
procedure TGraphF.Linear;
var
dispdat : double;
frequency : double;
max, min : double;
II: integer;
begin
max := 0;
min := 0;
dispdat := 0;
frequency := 0;
Series1.Clear;
for II := 0 to NF div 2 do begin
if Fourierf.StringGrid2.Cells[3, II + 1] <> '' then
dispdat := StrtoFloat(Fourierf.StringGrid2.Cells[3, II + 1]);
if Fourierf.StringGrid2.Cells[0, II + 1] <> '' then
frequency := StrtoFloat(Fourierf.StringGrid2.Cells[0, II + 1]);
Series1.AddXY(frequency, dispdat);
if dispdat > max then max := dispdat;
if dispdat < min then min := dispdat;
end;
chart1.LeftAxis.AutomaticMaximum := False;
chart1.LeftAxis.AutomaticMinimum := False;
if chart1.LeftAxis.Minimum >= max + (max - min) / 5 then begin
chart1.LeftAxis.Minimum := min;
chart1.LeftAxis.Maximum := max + (max - min) / 5;
end
else begin
chart1.LeftAxis.Maximum := max + (max - min) / 5;
chart1.LeftAxis.Minimum := min;
end;
BitBtn1.Caption := '入力ﾃﾞｰﾀｰ表示';
end;
//-------------- グラフ表示切り替え-----------------
procedure TGraphF.BitBtn1Click(Sender: TObject);
begin
if DispF then
begin
Chart1.Visible := False;
Chart2.Visible := True;;
inpdata; // データーグラフ描画
DispF := False;
end
else
begin
Chart2.Visible := False;
Chart1.Visible := True;;
DispF := True;
GraphF.Linear; // リニア描画
end;
end;
//--------------- 計算画面に戻り -----------------
procedure TGraphF.BitBtn2Click(Sender: TObject);
begin
Close;
end;
//-------------- 終了処理 ------------------------
procedure TGraphF.FormClose(Sender: TObject; var Action: TCloseAction);
begin
FourierF.Show;
end;
//-------------- 初期設定 ------------------------
procedure TGraphF.FormCreate(Sender: TObject);
var
Menus: HMENU;
begin
ClientHeight := 410;
ClientWidth := 600;
Top := (Screen.height - Height) div 2;
Left := (Screen.Width - Width) div 2;
BitBtn1.Top := 375;
BitBtn1.Left := 480;
BitBtn1.Width := 100;
BitBtn1.Height := 22;
BitBtn1.Font.Height := 12;
BitBtn2.Top := 370;
BitBtn2.Left := 350;
BitBtn2.Width := 60;
BitBtn2.Height := 25;
BitBtn2.Font.Height := 12;
Chart1.Left := 20;
Chart2.Left := 20;
Chart1.Width := 560;
Chart2.Width := 560;
Chart1.Visible := True;
Chart2.Visible := False;
// メニューの設定 クローズ 最大化 削除 前に戻る 追加
Menus := GetSystemMenu(Handle,false);
// DeleteMenu(Menus,SC_CLOSE,MF_BYCOMMAND);
DeleteMenu(Menus,SC_MAXIMIZE,MF_BYCOMMAND);
AppendMenu(Menus,MF_STRING, Mymenu,'前に戻る');
DrawMenuBar(Handle);
end;
end.
fourier.zip
各種プログラム計算例に戻る