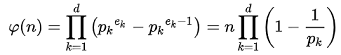オイラーのφ関数（トーシェント関数）

　正の整数 n に対して、1 以上 n 以下の自然数のうち n と互いに素なものの個数をφ(n)と書き、オイラーのφ関数またはトーシェント関数と言います。

例えば、nを6とすると、
　1/6
　2/6 -> 1/3
　3/6 -> 1/2
　4/6 -> 2/3
　5/6
となり、φ(6)=2 となり、最大公約数が１である値の数となります。

因数分解による方法

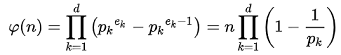　P_kはnの素因数

180の場合
　180=2³・3²・5 となり、180(1-1/2)(1-1/3)(1-1/5)=48個

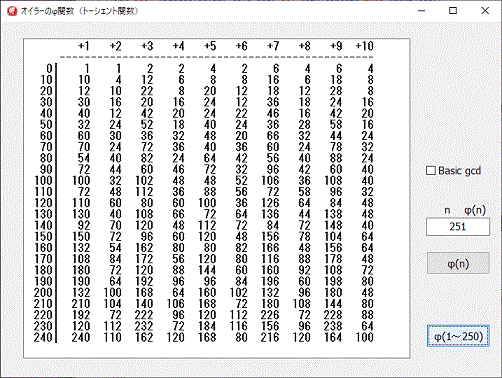　プログラムには、上記素因数分解による方法と、最大公約数による方法が組み込んであります。

プログラム

// Euler (オイラー) の関数
unit main;

interface

uses
  Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
  Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.Buttons, Vcl.ExtCtrls;

type
  TForm1 = class(TForm)
    Memo1: TMemo;
    BitBtn1: TBitBtn;
    BitBtn2: TBitBtn;
    LabeledEdit1: TLabeledEdit;
    CheckBox1: TCheckBox;
    procedure BitBtn1Click(Sender: TObject);
    procedure BitBtn2Click(Sender: TObject);
  private
    { Private 宣言 }
  public
    { Public 宣言 }
  end;

var
  Form1: TForm1;

implementation

{$R *.dfm}

// Eulerの関数に沿った基本的なプログラム
// 最大公約数が1である値をカウントします。
function phi_gcd(n : cardinal): cardinal;
var
  i, res : cardinal;

  // 最大公約数
  function gcd(a, b : cardinal): cardinal;
  var
    tmp : cardinal;
  begin
    while b > 0 do begin
      tmp := a mod b;
      a := b;
      b := tmp;
    end;
    result := a;
  end;

begin
  res := 1;                           // 分子1の分
  for i := 2 to n - 1 do
    if gcd(i, n) = 1 then inc(res);   // 最大公約数が1だったらインクリメント
  result := res;
end;

//---------------------------------------
// 積公式  素因数分解による
// φ(n)＝n・Π(1-1/p)
// p は n の素因子全体にわたる
function phi(n : cardinal): cardinal;
var
 p, t : cardinal;
begin
  t := n;
  if n mod 2 = 0 then begin       // 偶数2
    t := t div 2;                 // t = t(1-1/p)  = t/2
    repeat
      n := n div 2;
    until n mod 2 <> 0;
  end;
  p := 3;                         // 3以上奇数
  while n div p >= p do begin
    if n mod p = 0 then begin
      t := (t div p) * (p - 1);   // t = t(1-1/p)
      repeat
        n := n div p;
      until n mod p <> 0;
    end;
    inc(p, 2);
  end;
  if n > 1 then t := (t div n) * (n - 1);   // 最後の値
  result := t;
end;

//-------------------------------------------
procedure TForm1.BitBtn1Click(Sender: TObject);
const
  sp = ' ';
var
  i, j, k, h : cardinal;
  LL, s : string;
begin
  memo1.Clear;
  memo1.Font.Name := 'ＭＳ ゴシック';
  LL := '     ';
  for i := 1 to 10 do begin
    s := '+' + inttostr(i);
    h := 4 - length(s);
    for k := 0 to h do s := sp + s;
    LL := LL + s;
  end;
  memo1.Lines.Append(LL);
  LL := '     ';
  for i := 1 to 50 do LL := LL + '-';
  memo1.Lines.Append(LL);
  for i := 0 to 24 do begin
    s := intTostr(i * 10);
    h := 3 - length(s);
    for k := 0 to h do s := sp + s;
    s := s + '|';
    LL := s;
    for j := 1 to 10 do begin
      if checkbox1.Checked then
        s := intTostr(phi_gcd(10 * i + j))
      else
        s := intTostr(phi(10 * i + j));
      h := 4 - length(s);
      for k := 0 to h do s := sp + s;
      LL := LL + s;
    end;
    memo1.Lines.Append(LL);
  end;
end;

procedure TForm1.BitBtn2Click(Sender: TObject);
var
  x, y: cardinal;
  ch : integer;
begin
  val(labelededit1.Text, x, ch);
  if ch <> 0 then begin
    application.MessageBox('入力値に間違いがあれます','注意',0);
    exit;
  end;
  memo1.Clear;
  memo1.Font.Name := 'Tahoma';
  memo1.Lines.Append('オイラーのφ関数（トーシェント関数）');
  if checkbox1.Checked = true then
    y := phi_gcd(x)
  else
    y := phi(x);
  memo1.Lines.Append('φ(' + inttostr(x) + ')= ' + inttostr(y));
end;

end.

　Eulers_totient_function.zip

　　三角関数、逆三角関数、その他関数、 連立一次方程式の解法　に戻る