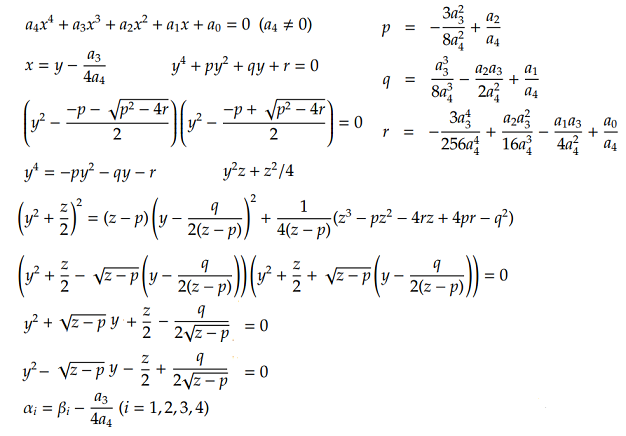2018/12/29 プログラム修正
1. Doble精度計算にメモリーリークがあったので、修正しました。
2.
計算結果の出力をImageからMemoに変え、テキストのコピーが出来るようにしました。
四、三、二、一次方程式の解法
四次~一次迄解法できるプログラムを作成しました。
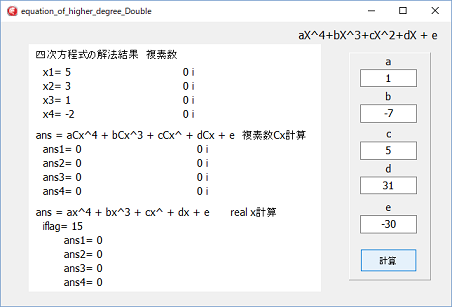 左図は、四次から一次迄解解法出来るプログラムの実行画面です。
左図は、四次から一次迄解解法出来るプログラムの実行画面です。
aの項がゼロでなければ、四次で、ゼロを入れると三次になります。
順次b,c,とゼロを入れることにより、二次、一次となります。
四次、三次、二次方程式の解法は、楕円同士の交点を求めるプログラムで既に使用しているのですが、そこで使用しているプログラムは、楕円の交点を求めるのには、問題なく解を得ることが出来るのですが、楕円のプログラムでは発生しない値を入れると、正しい解を得られない事とがあります。
そこで、インターネットで高次方程式の解法の資料と、新たなプログラムを探し、一応問題がないであろうプログラムをDelphiで作成しました。
基本的には、Cで組まれたプログラムを、方程式の解法の資料で検証しながらDelphiiに移植しました。
左図は、精度Doubleで作成したプログラムの実行画面ですが、四次方程式の解法にには、桁数が不足するので、多倍長計算のプログラムも作成しました。
計算が正しいかどうかは、回答のXの値で、計算して答えがゼロになることで判断します。
計算結果は、全て複素数形式となります。
aの項はXの四乗なので、桁落ちによる誤差の発生が出やすくなるので注意してください。
aの項からeの項に向かって絶対値が順に小さくなるか反対に大きくるような値であれば、結構大きな桁の差の値を入れても、正しい解を得ることが出来ます。
楕円同士の交点を求めている、四次方程式の解法の問題が判明しました。
四次方程式 ax^4 + bx^3 + cx^2 + dx + e = 0
の b と d がゼロの時は、 ax^4 + cx^2 + e = 0 となり、 y = x^2 とすると、ay^2 + cy + e = 0
の二次方程式を解き、y を求めてから、yの√で 解を求めるのですが、これが抜けています。
楕円の交点を求める場合、 b と
d が同時にゼロに成なっても、解ける値となっているので問題ありません、楕円の基準座標を、ゼロ度から30°或いは33°にすることによって実現されています。
基準座標の角度をゼロ度以外にするの本来の目的は、bとdが同時にゼロに成っても解が得られるようにする為ではないのですが、角度の変更により、解ける値だけが発生するようになったようです。
一次方程式
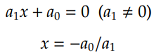 一次式については、特に説明は不要と思います。
一次式については、特に説明は不要と思います。
二次方程式
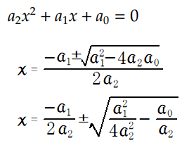 二次方程式は、一般的な計算方法です。
二次方程式は、一般的な計算方法です。
複素数計算をする為に、ルートの中と、外で別々に計算をします。
ルートが開ければ、複素数の虚数部を 0 とし ルートの中がマイナスでルートを開くことが出来なければ、絶対値の√の値を複素数の虚数部の値とします。
a2, a1, a0 を
複素数として、複素数の加減算、乗除算、√の計算が出来れば、方程式どうりに計算することにより 複素数として、x
の値を得ることが出来ます。
三次方程式
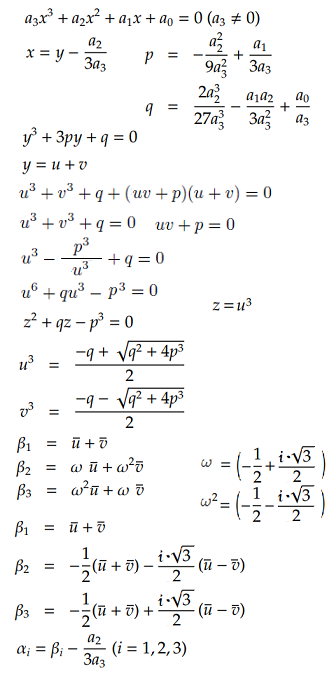 三次になると、少し複雑になります。
三次になると、少し複雑になります。
a3の項を1にすることにより、計算が簡単になりますが、方程式なので省略せずに表記しています。
Xを y-a2/(3a3) で置き換え
yの三次式に整理することにより、y3+3py+q
= 0 の式と、pとqの値を導き出すことが出来ます。
更に、y = u + v とし、y に代入して、u3 + v3
+ q + (uv + p)(u + v) = 0 を得ます。
これを満足するのは、 u3 + v3
+ q = 0 、uv + p = 0 なので u3 - p3/u3 + q = 0 u3、v3は z
= u3 とすると二次方程式 z2 + qz - p3 = 0 の解となります。
u,vを複素数とし、1の複素数の三乗根を ω = -1/2 + (√-3) /
2 とすると y3 + 3py + q = 0 の解は β1,
β2, β3 の三個となります。
* ω3
= 1
更に、x = y - a2/(3a3) としているので、βn - a2/(3a3)が、三次方程式の解
xn となります。
最初の解の、虚数部は必ずゼロです。
以上が三次方程式の解の説明です。
プログラムは、a3を1にして計算を簡単にしています。
方程式の解の説明には不足している部分があるかもしれませんが、プログラムは正しい解を出します。
解は全て複素数形式です。
四次方程式
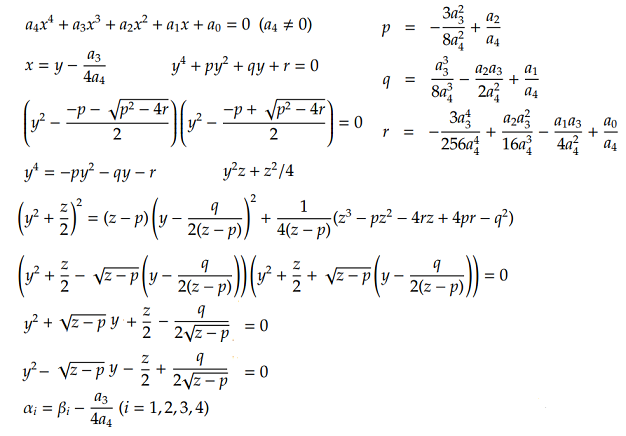
四次方程式は、三次方程式の解を利用する事により意外と簡単になっています。
x = y-a3/(4a4) で x を置き換え整理すると、y4
+ py2 + qy + r = 0 を得、三乗の項を消去できます。
更に、qが0の時は、これを因数分解出来ます。
これでyの値を求めても良いのですが、
qが0なので、y2= X とすると X2
+ pX + r = 0 となり、二次方程式を解くことで y2 の値を得ることが出来 √y で y の値βi となります。
q が 0でない時は、更に方程式の変換を行います。
y4 = -py2 - qy - r の両辺に y2z + z2/4 を加算し、式の変形をおこないます。
z3 - pz2 - 4rz + 4pr -
q2 が 0 となる z の値を三次方程式の解から求めれば、因数分解が出来ます。
三次方程式の解の一つは必ず虚数部がゼロとなるので、これを使用します。
因数分解した結果は y の二次方程式となるので、これの解を求めれば4個のy値 βi が得られます。
x の値は x = y-a3/(4a4) となっているので、βi
からa3/(4a4) を差し引けば、四次方程式の解 x を求める事が出来ます。
プログラム
方程式の解法に複素数を使用します。
演算精度Doubleの場合は複素数の変数は、Variantとして宣言し、複素数を作成します。
四則演算、+,-,*,/はそのまま使用することが出来ます。
二次、一次方程式は複素数に対する複素数の解答なので、実数値は虚数部ゼロとして複素数に変換してから入力します。
四次、三次は、実数値に対する複素数の解答です。
解答は全て複素数となります。
プログラムの中の定数の扱いの注意点 特に 0.5 0.25 0.125等の小数点表示 分母の値が2nの値です。
0.5 は1/2、 0.25 は 1/4 の様にします。
定数として与える場合は、K = 1/2 の様にします。
浮動小数点変換の誤差があり、0.5 は 1/2 に対して、Doubleの場合小数点以下16桁辺りに誤差がでます。
デバッグ上の表示では、0.5と表示されるので注意が必要です。
小さな値の整数は浮動小数点に変換しても誤差が出ません。
1 / 2 の 0.5 は、誤差の無い
0. 5となります。
n乗根を求める計算の場合特に注意が必要です。
unit main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.ExtCtrls, Vcl.StdCtrls, System.Math, System.Varcmplx;
type
TForm1 = class(TForm)
Panel1: TPanel;
Edit_c: TLabeledEdit;
Edit_b: TLabeledEdit;
Edit_d: TLabeledEdit;
Edit_a: TLabeledEdit;
Button1: TButton;
Label1: TLabel;
Edit_e: TLabeledEdit;
Memo1: TMemo;
procedure FormCreate(Sender: TObject);
procedure Button1Click(Sender: TObject);
private
{ Private 宣言 }
function datainput(var a, b, c, d, e: double): boolean;
function quartic_equation_c(a, b, c, d, e: double; var x: array of double): byte;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
//------------------------------------------------------------
// 複素数答えの構造体
type
TCans = record
n: integer;
ans: array[0..3] of Variant;
end;
// 複素数 real=0 Imaginary=0 の作成
var
Czero : Variant;
// 複素数の生成
function Varcomplex(a, b: double): Variant;
begin
result := varascomplex(result);
result.real := a;
result.Imaginary := b;
end;
// 複素数のゼロ判定 x=0 true x<> 0 false
function cis0(x: Variant): boolean;
begin
result := false;
if (x.real = 0) and (x.Imaginary = 0) then result := true;
end;
// 複素数の平方根
function csqrt(x: Variant): Variant;
var
len: double;
begin
result := Varascomplex(result);
if x.Imaginary = 0 then begin
if x.real >= 0 then result := VarComplex(sqrt(x.real), 0)
else result := VarComplex(0.0, sqrt(-x.real));
end
else begin
len := sqrt(x.real * x.real + x.Imaginary * x.Imaginary);
result.real := sqrt((len + x.real) / 2);
result.Imaginary := sqrt((len - x.real) / 2);
if x.Imaginary < 0 then result.Imaginary := -result.Imaginary;
end;
end;
// 立方根
function cbrt(x: double): double;
begin
result := power(abs(x), 1/3);
if x < 0 then result := -result;
end;
// 複素数の立方根
function ccbrt(x: Variant): Variant;
var
len, theta: double;
begin
result := VarasComplex(result);
if x.Imaginary = 0 then begin
result := VarComplex(cbrt(x.real), 0);
exit;
end;
len := cbrt(sqrt(x.real * x.real + x.Imaginary * x.Imaginary));
theta := arctan2(x.Imaginary, x.real) / 3;
result.real := len * cos(theta);
result.Imaginary := len * sin(theta);
end;
// 複素数一次方程式の解法
function cequation1(a, b: Variant): TCans;
var
i : integer;
begin
for i := 0 to 3 do
result.ans[i] := Czero;
if cis0(a) then begin
if cis0(b) then result.n := -1
else result.n := 0;
end
else begin
result.n := 1;
result.ans[0] := -b / a;
end;
end;
// 複素数二次式の解法
function cequation2(a, b, c: Variant): TCans;
var
i : integer;
begin
for i := 0 to 3 do
result.ans[i] := Czero;
if cis0(a) then begin
result := cequation1(b, c); // 複素数一次
exit;
end;
b := (VarComplex(-1 / 2, 0) * b) / a;
c := c / a;
a := csqrt((b * b) - c); // 複素数√
result.ans[0] := b + a;
result.ans[1] := b - a;
result.n := 2;
end;
// 三次方程式の解法
function equation3(a, b, c, d: double): TCans;
var
w, w2, cA3, cm, cn : Variant;
A0, B0, C0, A3 : double;
p, q, p3, q2, m, n : double;
begin
if a = 0 then begin
w := VarComplex(b, 0);
w2 := VarComplex(c, 0);
cm := VarComplex(d, 0);
result := cequation2(w, w2, cm);
exit;
end;
A0 := b / a;
B0 := c / a;
C0 := d / a;
w := VarComplex(-1 / 2, sqrt(3) / 2); // 複素数1の三乗根 ω = (-1/2, 1/2√3i)
w2 := VarComplex(-1 / 2, sqrt(3) / -2); // 複素数1の三乗根 ω2 = (-1/2, -1/2√3i)
A3 := A0 / 3; // x = y-a/3 y3 + p y + q = 0
cA3 := VarComplex(A3, 0);
p := B0 - A0 * A3;
q := 2 * A3 * A3 * A3 - A3 * B0 + C0;
p3 := p / 3;
q2 := -q / 2;
d := q2 * q2 + p3 * p3 * p3; // 判別値 ルートの中の計算 q^2 + 4p^3
if d >= 0 then begin // d がマイナスで無ければ 全て虚数部 = 0
m := cbrt(q2 + sqrt(d)); // 立方根 (q2 + √d)^1/3
n := cbrt(q2 - sqrt(d)); // 立方根 (q2 - √d)^1/3
result.ans[0] := VarComplex(m + n - A3, 0); // 複素数 x = (y-a/3, 0i)
result.ans[1] := VarComplex(m, 0) * w + VarComplex(n, 0) * w2 - cA3; // 複素数 x = y - Ca/3
result.ans[2] := VarComplex(m, 0) * w2 + VarComplex(n, 0) * w - cA3; // 複素数 x = y - Ca/3
end
else begin
d := sqrt(abs(d)); // dがマイナスだったら 虚数値di
cm := ccbrt(VarComplex(q2, d)); // 複素数立方根 (q2, √di)^1/3
cn := ccbrt(VarComplex(q2, -d)); // 複素数立方根 (q2,-√di)^1/3
result.ans[0] := cm + cn - cA3; // ans[0] 虚数部 = 0 複素数 x = y - Ca/3
result.ans[1] := cm * w + cn * w2 - cA3; // ans[1] 虚数部 <> 0 複素数 x = y - Ca/3
result.ans[2] := cm * w2 + cn * w - cA3; // ans[2] 虚数部 <> 0 複素数 x = y - Ca/3
end;
result.n := 3;
end;
// 四次方程式の解法
// X^4 + AX^2 + BX + C = 0
function equation4_sub(A0, B0, C0: double): TCans;
var
res : TCans;
x1, x2 : Variant;
Y, b1, c1, b2, c2: Variant;
L, M, N : double;
res1, res2 : TCans;
B, C, D : double;
begin
if B0 = 0 then begin // B0 = 0
Y := VarComplex(1.0, 0);
b1 := VarComplex(A0, 0);
c1 := VarComplex(C0, 0);
res := cequation2( Y, b1, c1); // X^2 = y 二次式の解法 y^2 + A0y + C0
x1 := csqrt(res.ans[0]); // x = √y
x2 := csqrt(res.ans[1]);
res.ans[0] := x1;
res.ans[1] := -x1;
res.ans[2] := x2;
res.ans[3] := -x2;
res.n := 4;
result:= res;
end
else begin // B0 <> 0
B := -A0 ; // X^4 = -AX^2 - BX - C = 0 両辺に X^2L + L^2/4 加算 式変形
C := 4 * -C0; // 三次式部 (L^3 - AL^2 - 4ACL + 4AC- B^2) 取り出し
D := 4 * A0 * C0 - B0 * B0; // 三次方程式 L^3 - AL^2 - 4ACL + 4AC- B^2 = 0
res1 := equation3( 1, B, C, D); // 三次解法(1, -A, -4C, 4AC - B^2)
// 因数分解 解法 -------------------------
L := res1.ans[0].real; // L
M := A0 - L; // M = A0 - L
N := B0 / (2 * M); // N = B0 / 2M
Y := csqrt(VarComplex(-M, 0)); // Y = √(-M, 0i) -M = L-A0
b1 := -Y; // b1 = -Y
c1 := VarComplex(L / 2, 0) - Y * VarComplex(N, 0); // c1 = (L / 2, 0i) - Y(N, 0i)
b2 := Y; // b2 = Y
c2 := VarComplex(L / 2, 0) + Y * VarComplex(N, 0); // c2 = (L / 2, 0i) + Y(N, 0i)
res1 := cequation2(VarComplex(1, 0), b1, c1); // y = X 複素数二次 (!, 0i)y^2 + b1y + c1 = 0
res2 := cequation2(VarComplex(1, 0), b2, c2); // y = X 複素数二次 (!, 0i)y^2 + b2y + c2 = 0
//----------------------------------------
res1.ans[2] := res2.ans[0];
res1.ans[3] := res2.ans[1];
res1.n := 4;
result := res1;
end;
end;
// 四次方程式の解法 三乗項X^3の消去
function equation4sub(a, b, c, d: double): TCans;
var
A0, B0, C0: double;
aa : double;
ca4 : Variant;
res : TCans;
i : integer;
begin
aa := a * a;
ca4 := VarComplex(a / 4, 0); // 複素数CX = (a/4,0)
// x = X - a/4 X^4 + A0X^2 + B0X + C0=0
A0 := b - (3 / 8) * aa;
B0 := c + a * aa / 8 - a * b / 2;
C0 := d - (3 / 256) * aa * aa + aa * b / 16 - a * c / 4;
res := equation4_sub(A0, B0, C0);
for i := 0 to 3 do
res.ans[i] := res.ans[i] - ca4; // x = X - a/4
result := res;
end;
// 四次方程式の解法
function equation4(a, b, c, d, e: double): TCans;
begin
if a = 0 then begin // ax^4 a=0 なら三次方程式解法
result := equation3(b, c, d, e);
exit;
end;
result:= equation4sub(b / a, c / a, d / a, e / a); // 四次方程式解法 x^4+b/ax^3+c/ax^2+d/ax+e/a = 0
end;
// ax^4 + bx^3 + cx^ + dx + e の計算
function poly4(a, b, c, d, e: double; x: Variant): Variant;
var
xx, xxx, xxxx : Variant;
ar, br, cr, dr, er: Variant;
begin
xx := x * x;
xxx := xx * x;
xxxx := xx * xx;
ar := VarComplex(a, 0) * xxxx;
br := VarComplex(b, 0) * xxx;
cr := VarComplex(c, 0) * xx;
dr := VarComplex(d, 0) * x;
er := VarComplex(e, 0);
result := ar + br + cr + dr + er;
end;
//--------------------------------------------------
// 一次二次三次四次方程式の解法
//--------------------------------------------------
function TForm1.quartic_equation_c(a, b, c, d, e: double; var x: array of double): byte;
const
YY = 90;
var
res : TCans;
j, k : integer;
rc : Variant;
i : array[0..3] of double;
rcr, rci : array[0..3] of double;
lng : integer;
tout : string;
function roundx(x: double):double; // 小数点10桁以下丸め
var
ix : int64;
x10 : double;
begin
if abs(x) < 1E10 then begin
x10 := x * 1E10;
ix := round(x10);
result := ix / 1E10;
end
else result := x;
end;
begin
result := 0;
res := equation4(a, b, c, d, e);
for j := 0 to res.n - 1 do begin
rc := poly4(a, b, c, d, e, res.ans[j]);
x[j] := res.ans[j].real;
i[j] := res.ans[j].Imaginary;
rcr[j] := rc.real;
rci[j] := rc.Imaginary;
end;
k := 1;
if res.n > 0 then begin
for j := 0 to res.n -1 do begin
if i[j] = 0 then result := result or k;
k := k * 2;
end;
with Memo1.Lines do begin
if res.n = 4 then Add(' 四次方程式の解法結果 複素数');
if res.n = 3 then Add(' 三次方程式の解法結果 複素数');
if res.n = 2 then Add(' 二次方程式の解法結果 複素数');
if res.n = 1 then Add(' 一次方程式の解法結果');
Add('');
if res.n > 0 then
for j := 0 to res.n - 1 do begin
tout := (' x' + intTostr(j + 1) + '= ' + floattostr(roundx(x[j])));
lng := length(tout);
for k := 0 to 22 - lng do tout := tout + ' ';
tout := tout + floattostr(i[j]) + ' i';
add(tout);
end;
Add('');
Add('ans = aCx^4 + bCx^3 + cCx^ + dCx + e 複素数Cx計算');
for j := 0 to res.n - 1 do begin
tout := ' ans' + intTostr(j + 1) + '= ' + floatTostr(roundx(rcr[j]));
lng := length(tout);
for k := 0 to 22 - lng do tout := tout + ' ';
tout := tout + floatTostr(rci[j]) + ' i';
add(tout);
end;
end;
end;
end;
//-----------------------------------------------------------
function TForm1.datainput(var a, b, c, d, e: double): boolean;
var
ch: integer;
begin
result := false;
val(edit_a.Text, a, ch);
if ch <> 0 then begin
application.MessageBox('aの値が数字ではありません。','注意', 0);
exit;
end;
val(edit_b.Text, b, ch);
if ch <> 0 then begin
application.MessageBox('bの値が数字ではありません。','注意', 0);
exit;
end;
val(edit_c.Text, c, ch);
if ch <> 0 then begin
application.MessageBox('cの値が数字ではありません。','注意', 0);
exit;
end;
val(edit_d.Text, d, ch);
if ch <> 0 then begin
application.MessageBox('dの値が数字ではありません。','注意', 0);
exit;
end;
val(edit_e.Text, e, ch);
if ch <> 0 then begin
application.MessageBox('eの値が数字ではありません。','注意', 0);
exit;
end;
result := true;
end;
procedure TForm1.FormCreate(Sender: TObject);
begin
top := (screen.Height - height) div 2;
left := (screen.Width - width) div 2;
image1.Canvas.Font.Height := 18;
end;
procedure TForm1.Button1Click(Sender: TObject);
var
a, b, c, d, e : double;
iflag : byte;
x : array[0..3] of double;
k, i, j : integer;
xans : double;
function roundx(x: double):double; // 小数点10桁以下丸め
var
ix : int64;
x10 : double;
begin
if abs(x) < 1E10 then begin
x10 := x * 1E10;
ix := round(x10);
result := ix / 1E10;
end
else result := x;
end;
begin
if not datainput(a, b, c, d, e) then exit;
Memo1clear;
iflag := quartic_equation_c(a, b, c, d, e, x); // 方程式の解法
Memo1.Lines.Add('');
Memo1.Lines.Add('ans = ax^4 + bx^3 + cx^ + dx + e real x計算');
Memo1.Lines.Add(' iflag= ' + intTostr(iflag));
k := 1;
for i := 0 to 3 do begin
if iflag and k = k then begin
xans := a * x[i] * x[i] * x[i] * x[i]
+ b * x[i] * x[i] * x[i]
+ c * x[i] * x[i]
+ d * x[i] + e;
Memo1.Lines.Add(' ans' + inttostr(i + 1) + '= ' + floatTostr(roundx(xans)));
end;
k := k * 2;
end;
end;
Initialization
// 複素数初期化
Czero := VarComplex(0, 0);
end.
多倍長演算
多倍長演算ならば、有効桁数50桁以上の精度を得ることが出来ます。
FPUを使用していないので、演算時間は長くなります。
MPArithからmparith_2018-11-27.zipをダウンロードします。
ファイルの日付が変わるので、変わっていたら新しいのをダウンロードして下さい。
Zipファイルを解凍して、解凍したフォルダーにパス(ツール->オプション->Delphiオプション->ライブラリ->ライブラリパス)を追加し、Uses に mp_types, mp_real, mp_cmplx, mp_baseを追加すれば使用可能になります。
一般の四則演算(=+-*/)は使用できず全て専用のルーチンとなるのでプログラムが長くなります。
使用方法は、ホームページ及び、helpファイルを見れば分かりますが、helpファイルは古いタイプなので、Win10で見るためには、変換をするか、WinHlp32.exeを入れ替える必要があります。
unit main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.ExtCtrls, Vcl.StdCtrls, System.Math, mp_types, mp_real,
mp_cmplx, mp_base;
type
TForm1 = class(TForm)
Panel1: TPanel;
Edit_c: TLabeledEdit;
Edit_b: TLabeledEdit;
Edit_d: TLabeledEdit;
Edit_a: TLabeledEdit;
Button1: TButton;
Label1: TLabel;
Edit_e: TLabeledEdit;
Memo1: TMemo;
procedure FormCreate(Sender: TObject);
procedure Button1Click(Sender: TObject);
private
{ Private 宣言 }
function quartic_equation_c(a, b, c, d, e: mp_float; var ansX : array of double): byte;
function datainput(var a, b, c, d, e: mp_float; var data: array of double): boolean;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
//------------------------------------------------------------
// 複素数構造体
// 解法結果 解答構造体
type
CAns = record
n: integer; // 次数
ans: array[0..3] of mp_complex; // 解答complex(re, im)
end;
// 解答構造体のコピー
procedure CAcopy(a: CAns; var b: CAns);
var
i : integer;
begin
for i := 0 to 3 do begin
mpc_copy(a.ans[i], b.ans[i]);
end;
b.n := a.n;
end;
// real -> 複素数(r, 0i);
procedure mp_complex_xr_im0(x: mp_float; var ans: mp_complex);
begin
mpf_copy(x, ans.re);
mpf_set0(ans.im);
end;
// 多倍長立方根
procedure cbrt(x: mp_float; var ans: mp_float);
begin
if not s_mpf_is0(x) then mpf_cbrt(x, ans) // ゼロでなかったら立方根
else mpf_set0(ans); // ゼロだったらゼロ
end;
// 複素数立方根
procedure ccbrt(x: mp_complex; var ans: mp_complex);
begin
if mpc_is0(x) then // 複素数がゼロだったら
mpc_set0(ans) // 答え0
else // ゼロでなければ立方根
mpc_nroot(x, 3, ans); // ans = x^1/3
end;
// 複素数一次式の解法
procedure Cequation1(a, b: mp_complex; var ans: CAns);
var
i : integer;
c : mp_complex;
begin
mpc_init(c);
for i := 0 to 3 do
mpc_set0(ans.ans[i]); // ans.ans クリア
if mpc_is0(a) then begin // aがゼロだったら
ans.n := 0; // 解無し
end
else begin // a がゼロでなければ
ans.n := 1;
mpc_chs(b, c); // b を右辺に移動
mpc_div(c, a, ans.ans[0]) // ans.ans[0] = -b / a
end;
mpc_clear(c);
end;
// 複素数二次式の解法
procedure cequation2(a, b, c: mp_complex; var ans: CAns);
var
i : integer;
ca, cb, cc : mp_complex;
d, e : Mp_float;
cf, cg : mp_complex;
begin
mpc_init5(cf, cg, ca, cb, cc);
mpf_init2(d, e);
for i := 0 to 3 do
mpc_set0(ans.ans[i]); // ans.ans[i]のクリア
if mpc_is0(a) then begin // a がゼロだったら
Cequation1(b, c, ans); // 複素数一次式
end
else begin // a がゼロでなかったら
mpf_set_int(d, -2); // -2
mpf_inv(d, e); // -1/2 -0.5
mp_complex_xr_im0(e, cf); // (-0.5, 0i)
mpc_mul(cf, b, cg); // (-0.5, 0i)b
mpc_div(cg, a, cb); // cb = (-0.5, 0i)b / a
mpc_div(c, a, cc); // cc = c / a
mpc_sqr(cb, cf); // cb^2
mpc_sub(cf, cc, cg); // cb^2 - c/a
mpc_sqrt(cg, ca); // ca = √(cb^2 - c/a)
mpc_add(cb, ca, ans.ans[0]); // ans.ans[0] = cb + ca
mpc_sub(cb, ca, ans.ans[1]); // ans.ans[1] = cb - ca
ans.n := 2; // n = 2
end;
mpc_clear5(cf, cg, ca, cb, cc);
mpf_clear2(d, e);
end;
// 三次式の解法
procedure equation3(a, b, c, d: mp_float; var ans: CAns);
var
w, w2, cA3, cm, cn : mp_complex;
ctmp0, ctmp1, ctmp2 : mp_complex;
A0, B0, C0, A3 : mp_float;
p, q, p3, q2 : mp_float;
m, n, md : mp_float;
m05, f05, tmp : mp_float;
begin
mpc_init4(w, w2, cA3, cm);
mpc_init4(ctmp0, ctmp1, ctmp2, cn);
mpf_init4(A0, B0, C0, A3);
mpf_init4(p, q, p3, q2);
mpf_init3(m, n, md);
mpf_init3(m05, f05, tmp);
if mpf_is0(a) then begin // a がゼロなら複素数 二次式の解法
mp_complex_xr_im0(b, ctmp0); // (b, 0i)
mp_complex_xr_im0(c, ctmp1); // (c, 0i)
mp_complex_xr_im0(d, ctmp2); // (d, 0i)
cequation2(ctmp0, ctmp1, ctmp2, ans)
end
else begin
mpc_set0(ans.ans[3]); // ans.ans[3]のクリア
mpf_div(b, a, A0); // A0 = b/a
mpf_div(c, a, B0); // B0 = c/a
mpf_div(d, a, C0); // C0 = d/a
mpf_set_int(tmp, 2); // 2
mpf_inv(tmp, f05); // f05=1/2 0.5
mpf_chs(f05, m05); // m05=-1/2 -0.5
mpf_set_int(p, 3); // 3
mpf_sqrt(p, q); // √3
mpf_mul(f05, q, tmp); // 0.5*√3
mpc_set_mpf(w, m05, tmp); // w = (-0.5, 0.5*√3i)
mpf_chs(tmp, tmp); // -0.5*√3
mpc_set_mpf(w2, m05, tmp); // w2 = (-0.5, -0.5*√3i)
mpf_div_int(A0, 3, A3); // A0/3
mp_complex_xr_im0(A3, cA3); // cA3 = (A3, 0i)
mpf_mul(A0, A3, tmp); // A0A3
mpf_sub(B0, tmp, p); // p = B0-A0A3
mpf_expt_int(A3, 3, p3); // A3^3
mpf_mul_int(p3, 2, tmp); // 2A3^3
mpf_mul(A3, B0, p3); // A3B0
mpf_sub(tmp, p3, q2); // 2A3^3- A3B0
mpf_add(q2, C0, q); // q = 2A3^3- A3B0 + C0
mpf_div_int(p, 3, p3); // p3 = p/3
mpf_mul(m05, q, q2); // q2 = q/-2
mpf_expt_int(q2, 2, f05); // q2^2
mpf_expt_int(p3, 3, m05); // p3^3
mpf_add(f05, m05, tmp); // q2^2 + p3^3
if s_mpf_is_ge0(tmp) then begin // q2^2 + p3^3 >= 0 なら
mpf_sqrt(tmp, md); // md = √(q2^2 + p3^3)
mpf_add(q2, md, tmp); // q2+md
cbrt(tmp, m); // m = (q2+md)^1/3
mpf_sub(q2, md, tmp); // q2-md
cbrt(tmp, n); // m = (q2-md)^1/3
mpf_add(m, n, f05); // m+n
mpf_sub(f05, A3, tmp); // m+n-A3
mp_complex_xr_im0(tmp, ans.ans[0]); // ans.ans[0] = (m+n-A3, 0i)
mp_complex_xr_im0(m, cm); // (m, cmi)
mp_complex_xr_im0(n, cn); // (n, cni)
mpc_mul(cm, w, ctmp0); // (m, cmi)w
mpc_mul(cn, w2, ctmp1); // (n, cni)w2
mpc_add(ctmp0, ctmp1, ctmp2); // (m, cmi)w + (n, cni)w2
mpc_sub(ctmp2, cA3, ans.ans[1]); // ans.ans[1] = (m, cmi)w + (n, cni)w2 - cA3
mpc_mul(cm, w2, ctmp0); // (m, cmi)w2
mpc_mul(cn, w, ctmp1); // (n, cn)w
mpc_add(ctmp0, ctmp1, ctmp2); // (m, cmi)w2 + (n, cni)w
mpc_sub(ctmp2, cA3, ans.ans[2]); // ans.ans[2] = (m, cmi)w2 + (n, cni)w - cA3
end
else begin // (q2^2 + p3^3) < 0 なら
mpf_chs(tmp, tmp); // -q2^2 - p3^3
mpf_sqrt(tmp, md); // md = √(-q2^2 - p3^3)
mpc_set_mpf(ctmp0, q2, md); // (q2, mdi)
ccbrt(ctmp0, cm); // cm = (q2, mdi)^1/3
mpf_chs(md, md); // -md
mpc_set_mpf(ctmp1, q2, md); // (q2, -md)
ccbrt(ctmp1, cn); // cn = (q2, -md)^1/3
mpc_add(cm, cn, ctmp0); // cm + cn
mpc_sub(ctmp0, cA3, ans.ans[0]); // ans.ans[0] = cm + cn - cA3
mpc_mul(cm, w, ctmp0); // cm*w
mpc_mul(cn, w2, ctmp1); // cn*w2
mpc_add(ctmp0, ctmp1, ctmp2); // cm*w + cn*w2
mpc_sub(ctmp2, cA3, ans.ans[1]); // ans.ans[1] = cm*w + cn*w2 - cA3
mpc_mul(cm, w2, ctmp0); // cm*w2
mpc_mul(cn, w, ctmp1); // cn*w
mpc_add(ctmp0, ctmp1, ctmp2); // cm*w2 + cn*w
mpc_sub(ctmp2, cA3, ans.ans[2]); // ans.ans[2] = cm*w2 + cn*w - cA3
end;
ans.n := 3; // n = 3
end;
mpc_clear4(w, w2, cA3, cm);
mpc_clear4(ctmp0, ctmp1, ctmp2, cn);
mpf_clear4(A0, B0, C0, A3);
mpf_clear4(p, q, p3, q2);
mpf_clear3(m, n, md);
mpf_clear3(m05, f05, tmp);
end;
// X四次方程式の解法
procedure equation4_sub(A ,B, C: mp_float; var ans: CAns);
var
i : integer;
res, res1, res2 : Cans;
x1, x2 : mp_complex;
X, b1, c1, b2, c2: mp_complex;
ctmp : mp_complex;
L, M, N : mp_float;
fone, b0, c0, d0, tmp : mp_float;
begin
for i:= 0 to 3 do
mpc_init3(res.ans[i], res1.ans[i], res2.ans[i]);
mpc_init3(x1, x2, X);
mpc_init4(b1, c1, b2, c2);
mpf_init3(L, M, N);
mpf_init4(fone, b0, c0, d0);
mpf_init(tmp);
mpf_init2(ctmp.re, ctmp.im);
mpf_set1(fone); // fone = 1
if mpf_is0(B) then begin // B=0だったら
mpc_set1(X); // (1, 0i)
mp_complex_xr_im0(A, b1); // (A, 0i)
mp_complex_xr_im0(C, c1); // (c, 0i)
cequation2(X, b1, c1, res); // 複素数二次方程式の解法(1, A, C)
mpc_sqrt(res.ans[0], x1); // x1=√res.ans[0]
mpc_sqrt(res.ans[1], x2); // x2=√res.ans[1]
mpc_copy(x1, res.ans[0]); // res.ans[0] = x1
mpc_chs(x1, res.ans[1]); // res.ans[1] = -x1
mpc_copy(x2, res.ans[2]); // res.ans[2] = x2
mpc_chs(x2, res.ans[3]); // res.ans[3] = -x2
res.n := 4;
CAcopy(res, ans);
end
else begin // B=0でなかったら
mpf_chs(A, b0); // b0 = chs(A)
mpf_mul_int(C, 4, c0); // c0 = 4C
mpf_mul(c0, A, tmp); // tmp = 4AC
mpf_sqr(B, d0); // d0 = B * B
mpf_sub(tmp, d0, d0); // d0 = 4AC-B^2
mpf_chs(c0, c0); // c0 = -4c
equation3(fone, b0, c0, d0, res1); // 三次方程式の解法
mpf_copy(res1.ans[0].re, L); // 三次最初の答え 最初の答えは必ず虚数部ゼロ
mpf_sub(A, L, M); // M = A-L
mpf_mul_int(M, 2, tmp); // 2M
mpf_div(B, tmp, N); // N = B/(2M)
mpf_chs(M, M); // -M
mp_complex_xr_im0(M, ctmp); // (-M,0i)
mpc_sqrt(ctmp, X); // X=√(-M,0i)
mpf_div_int(L, 2, tmp); // L/2
mp_complex_xr_im0(tmp, b2); // (L/2,0i)
mp_complex_xr_im0(N, c1); // (N,0i)
mpc_mul(X, c1, ctmp); // X(N,0i)
mpc_sub(b2, ctmp, c1); // c1 = (L/2,0i) - X(N,0i)
mpc_add(b2, ctmp, c2); // c2 = (L/2,0i) + X(N,0i)
mpc_chs(X, b1); // b1 = -X
mpc_copy(X, b2); // b2 = X
mpc_set1(ctmp); // ctmp = (1, 0i)
cequation2(ctmp, b1, c1, res1); // 複素数二次式の解法 (1,b1,c1)
cequation2(ctmp, b2, c2, res2); // 複素数二次式の解法 (1,b2,c2)
mpc_copy(res2.ans[0], res1.ans[2]); // res1.ans[2] = res2.ans[0]
mpc_copy(res2.ans[1], res1.ans[3]); // res1.ans[3] = res2.ans[1]
res1.n := 4; // n = 4
CAcopy(res1, ans); // ans = res1
end;
for i:= 0 to 3 do
mpc_clear3(res.ans[i], res1.ans[i], res2.ans[i]);
mpc_clear3(x1, x2, X);
mpc_clear4(b1, c1, b2, c2);
mpf_clear3(L, M, N);
mpf_clear4(fone, b0, c0, d0);
mpf_clear(tmp);
mpf_clear2(ctmp.re, ctmp.im);
end;
// 四次方程式の解法 三乗項x^3の消去
procedure equation4sub(a, b, c, d: mp_float; var ans: CAns);
var
i : integer;
A0, B0, C0 : mp_float;
aa, tmp, tmp1, tmp2: mp_float;
a4 : mp_complex;
res : CAns;
begin
mpf_init3(A0, B0, C0);
mpf_init4(aa, tmp, tmp1, tmp2);
mpf_init2(a4.re, a4.im);
for i := 0 to 3 do
mpc_init(res.ans[i]);
mpf_sqr(a, aa); // a^2
mpf_div_int(a, 4, tmp); // a/4
mp_complex_xr_im0(tmp, a4); // Ca4
mpf_div_int(aa, 8, tmp); // a^2 / 8
mpf_mul_int(tmp, 3, B0); // 3/8*a^2
mpf_sub(b, B0, A0); // A0 = b-3/8*a^2
mpf_mul(tmp, a, C0); // a^3/8
mpf_mul(a, b, tmp); // ab
mpf_div_int(tmp, 2, tmp2); // ab/2
mpf_add(c, C0, tmp1); // c+a^3/8
mpf_sub(tmp1, tmp2, B0); // B0 = c+a^3/8-ab/2
mpf_sqr(aa, tmp); // a^4
mpf_div_int(tmp, 256, tmp1); // a^4/256
mpf_mul_int(tmp1, 3, tmp); // 3/256*a^4
mpf_mul(aa, b, tmp2); // a^2b
mpf_div_int(tmp2, 16, tmp1); // a^2b/16
mpf_mul(a, c, C0); // ac
mpf_div_int(C0, 4, tmp2); // ac/4
mpf_sub(d, tmp, C0); // d-3/256*a^4
mpf_add(C0, tmp1, tmp); // d-3/256*a^4+d+a^2b/16
mpf_sub(tmp, tmp2, C0); // C0 = d-3/256*a^4+a^2b/16-ac/4
equation4_sub(A0, B0, C0, res); // X^4 + A0X^2 + B0^2 + C0 = 0 による四次式の解法
for i := 0 to 3 do
mpc_sub(res.ans[i], a4, res.ans[i]); // res - a4
CAcopy(res, ans); // ans = res
mpf_clear3(A0, B0, C0);
mpf_clear4(aa, tmp, tmp1, tmp2);
mpf_clear2(a4.re, a4.im);
for i := 0 to 3 do
mpc_clear(res.ans[i]);
end;
// 四次方程式の解法
procedure equation4(a, b, c, d, e: mp_float; var ans: CAns);
var
b0, c0, d0, e0 : mp_float;
begin
mpf_init4(b0, c0, d0, e0);
if mpf_is0(a) then // a がゼロだったら
equation3(b, c, d, e, ans) // 三次式の解法
else begin // ゼロでなかったら
mpf_div(b, a, b0); // b0 = b / a
mpf_div(c, a, c0); // c0 = c / a
mpf_div(d, a, d0); // d0 = d / a
mpf_div(e, a, e0); // e0 = e / a
equation4sub(b0, c0, d0, e0, ans); // 四次式の解法
end;
mpf_clear4(b0, c0, d0, e0);
end;
// 複素数 aCx^4 + bCx^3 + cCx^2 + dCx + e の計算
procedure poly4(a, b, c, d, e: mp_float; x: mp_complex; var ans: mp_complex);
var
xx, xxx, xxxx : mp_complex;
ar, br, cr, dr, er: mp_complex;
a0, b0, c0, d0: mp_complex;
begin
mpc_init3(xx, xxx, xxxx);
mpc_init5(ar, br, cr, dr, er);
mpc_init4(a0, b0, c0, d0);
mpc_mul(x, x, xx); // Cx^2
mpc_mul(xx, x, xxx); // Cx^3
mpc_mul(xx, xx, xxxx); // Cx^4
mp_complex_xr_im0(a, a0); // Ca
mp_complex_xr_im0(b, b0); // Cb
mp_complex_xr_im0(c, c0); // Cc
mp_complex_xr_im0(d, d0); // Cd
mp_complex_xr_im0(e, er); // Ce
mpc_mul(a0, xxxx, ar); // Cq*Cx^4
mpc_mul(b0, xxx, br); // Cb*Cx^3
mpc_mul(c0, xx, cr); // Cc*Cx^2
mpc_mul(d0, x, dr); // Cd*Cx
mpc_add(ar, br, xx); // Cq*Cx^4 + Cb*Cx^3
mpc_add(cr, dr, xxx); // Cq*Cx^2 + Cb*Cx
mpc_add(xx, xxx, xxxx); // Cq*Cx^4 + Cb*Cx^3 + Cq*Cx^2 + Cb*Cx
mpc_add(xxxx, er, ans); // Cq*Cx^4 + Cb*Cx^3 + Cq*Cx^2 + Cb*Cx + Ce
mpc_clear3(xx, xxx, xxxx);
mpc_clear5(ar, br, cr, dr, er);
mpc_clear4(a0, b0, c0, d0);
end;
//--------------------------------------------------
// 一次二次三次四次方程式の解法
//--------------------------------------------------
function TForm1.quartic_equation_c(a, b, c, d, e: mp_float; var ansX: array of double): byte;
const
YY = 90;
var
xint : mp_int;
xx, lg, lc : mp_float;
res : Cans;
j, k : integer;
rc : mp_complex;
x, i : array[0..3] of mp_float;
rcr, rci : array[0..3] of mp_float;
tout : string;
lng : integer;
// 小数点50桁以下丸め
procedure roundX(var xir, xx, lg, lc: mp_float; var ii: mp_int);
begin
mpf_abs(xir, xx);
if mpf_is_gt(xx, lc) then exit; // 整数部が10桁以上の場合丸め無し
mpf_mul(xir, lg, xx);
mpf_round(xx, ii);
mpf_set_mpi(xx, ii);
mpf_div(xx, lg, xir);
end;
begin
for j := 0 to 3 do begin
mpc_init(res.ans[j]);
mpf_init4(x[j], i[j], rcr[j], rci[j]);
end;
mpc_init(rc);
mp_init(xint);
mpf_init3(xx, lg, lc);
result := 0;
equation4(a, b, c, d, e, res); // 方程式の解法
for j := 0 to res.n - 1 do begin
poly4(a, b, c, d, e, res.ans[j], rc); // 表示用四次計算
mpf_copy(res.ans[j].re, x[j]);
mpf_copy(res.ans[j].im, i[j]);
mpf_copy(rc.re, rcr[j]);
mpf_copy(rc.im, rci[j]);
end;
for j := 0 to res.n - 1 do ansX[j] := mpf_todouble(x[j]); // xの値double変換
k := 1;
for j := 0 to res.n - 1 do begin // 虚数ゼロの答え抽出
if mpf_is0(i[j]) then result := result or k;
K := K * 2;
end;
mpf_exp10i(50, lg);
mpf_exp10i(10, lc);
for j := 0 to res.n -1 do begin
roundX(x[j], xx, lg, lc, xint);
roundX(i[j], xx, lg, lc, xint);
roundX(rcr[j], xx, lg, lc, xint);
roundX(rci[j], xx, lg, lc, xint);
end;
if res.n > 0 then begin
with Memo1.Lines do begin
if res.n = 4 then Add(' 四次方程式の解法結果 複素数 多倍長');
if res.n = 3 then Add(' 三次方程式の解法結果 複素数 多倍長');
if res.n = 2 then Add(' 二次方程式の解法結果 複素数 多倍長');
if res.n = 1 then Add(' 一次方程式の解法結果 多倍長');
for j := 0 to res.n - 1 do begin
tout:= ' x' + inttostr(j + 1) + '= ' + string(mpf_decimal_alt(x[j], 50));
lng := length(tout);
for k := 0 to 61 - lng do tout := tout + ' ';
tout := tout + string(mpf_decimal_alt(i[j], 50)) + ' i';
Add(tout);
end;
Add('');
Add(' 検算 ans = aX^4 + bX^3 + cX^2 + dX + e');
for j := 0 to res.n - 1 do begin
tout := ' X' + intTostr(j + 1) + 'ans= ' + string(mpf_decimal_alt(rcr[j], 50));
lng := length(tout);
for k := 0 to 61 - lng do tout := tout + ' ';
tout := tout + string(mpf_decimal_alt(rci[j], 50)) + ' i';
Add(tout);
end;
end;
end;
for j := 0 to 3 do begin
mpc_clear(res.ans[j]);
mpf_clear4(x[j], i[j], rcr[j], rci[j]);
end;
mpc_clear(rc);
mp_clear(xint);
mpf_clear3(xx, lg, lc);
end;
// 入力データー処理
function TForm1.datainput(var a, b, c, d, e: mp_float; var data: array of double): boolean;
var
ch: integer;
ansistr: ansistring;
begin
result := false;
val(edit_a.Text, data[0], ch);
if ch <> 0 then begin
application.MessageBox('aの値が数字ではありません。','注意', 0);
exit;
end;
val(edit_b.Text, data[1], ch);
if ch <> 0 then begin
application.MessageBox('bの値が数字ではありません。','注意', 0);
exit;
end;
val(edit_c.Text, data[2], ch);
if ch <> 0 then begin
application.MessageBox('cの値が数字ではありません。','注意', 0);
exit;
end;
val(edit_d.Text, data[3], ch);
if ch <> 0 then begin
application.MessageBox('dの値が数字ではありません。','注意', 0);
exit;
end;
val(edit_e.Text, data[4], ch);
if ch <> 0 then begin
application.MessageBox('eの値が数字ではありません。','注意', 0);
exit;
end;
// 各値 a~e 多倍長へ読み込み
// テキストをmp_floatに変換します mpf_read_decimal は pansichar のみ対応です
// doubleから読み込むと浮動小数点の桁落ちがある為です。
ansistr := ansistring(edit_a.Text);
mpf_read_decimal(a, pansichar(ansistr));
ansistr := ansistring(edit_b.Text);
mpf_read_decimal(b, pansichar(ansistr));
ansistr := ansistring(edit_c.Text);
mpf_read_decimal(c, pansichar(ansistr));
ansistr := ansistring(edit_d.Text);
mpf_read_decimal(d, pansichar(ansistr));
ansistr := ansistring(edit_e.Text);
mpf_read_decimal(e, pansichar(ansistr));
result := true;
end;
// 初期設定
procedure TForm1.FormCreate(Sender: TObject);
begin
top := (screen.Height - height) div 2;
left := (screen.Width - width) div 2;
image1.Canvas.Font.Height := 18;
end;
procedure TForm1.Button1Click(Sender: TObject);
var
a, b, c, d, e : mp_float;
X : array[0..3] of double;
abcde: array[0..4] of double;
iflag : byte;
i, j, k : integer;
lng : integer;
tout : string;
// result = ax^4 + bx^3 + cx^2 + dx + e
function poly4d(x: double): double;
begin
result := abcde[0] * x * x* x * x + abcde[1] * x * x * x
+ abcde[2] * x * x + abcde[3] * x + abcde[4];
end;
// 小数点10桁以下丸め
function roundx(x: double): double;
var
ii : int64;
begin
if abs(x) < 1E5 then begin // 整数部が5桁以上の場合処理なし
x := x * 1E10;
ii := round(x);
result := ii / 1E10;
end
else result := x;
end;
begin
mpf_init3(a, b, c);
mpf_init2(d, e);
if datainput(a, b, c, d, e, abcde) then begin
Memo1.Clear;
iflag := quartic_equation_c(a, b, c, d, e, X); // 方程式の解法
Memo1.Lines.Add('');
Memo1.Lines.Add(' iflag= ' + intTostr(iflag));
j := 1;
Memo1.Lines.Add('');
Memo1.Lines.Add(' Double 8byte 表示');
for i := 0 to 3 do begin
if (iflag and j) <> 0 then begin
tout := ' X' + inttostr(i + 1) + '= ' + floatTostr(roundx(X[i]));
lng := length(tout);
for K := 0 to 35 - lng do tout := tout + ' ';
tout := tout + ('X' + inttostr(i + 1) + 'ans= ' + floatTostr(roundx(poly4d(X[i]))));
Memo1.Lines.Add(tout);
end;
j := j * 2;
end;
end;
mpf_clear3(a, b, c);
mpf_clear2(d, e);
end;
end.
 equation_of_higher_degree.zip
equation_of_higher_degree.zip
各種プログラム計算例に戻る
 左図は、四次から一次迄解解法出来るプログラムの実行画面です。
左図は、四次から一次迄解解法出来るプログラムの実行画面です。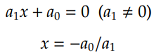 一次式については、特に説明は不要と思います。
一次式については、特に説明は不要と思います。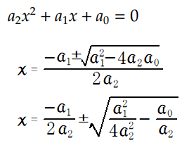 二次方程式は、一般的な計算方法です。
二次方程式は、一般的な計算方法です。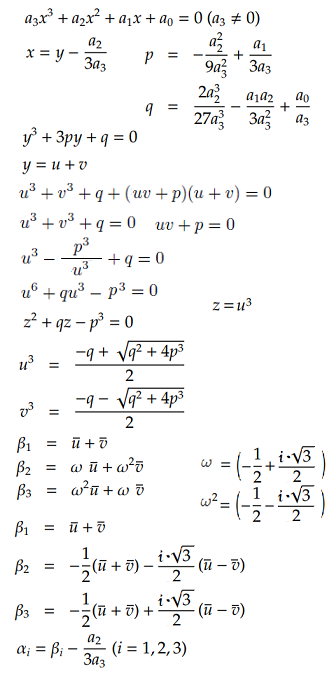 三次になると、少し複雑になります。
三次になると、少し複雑になります。