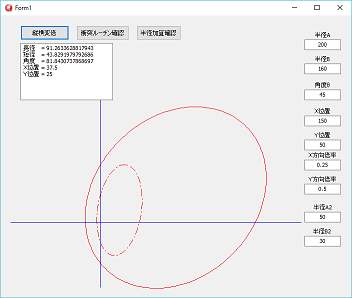
左図は、大きい楕円に対して、Ｘ方向０．２５倍、Ｙ方向０．５倍の変倍をした楕円をあらわしています。元の頂点の位置を縦横違う変倍率で変倍すると、頂点の位置が変倍後の頂点の位置にならないことが、楕円の変倍の難しさとなっています。
角度のある楕円の縦横変倍
角度のある楕円を変倍する場合、長辺と短辺の値や角度が、四角や三角と異なり、単純に求める事が出来ません。
色々探した結果、"楕円と楕円の衝突"http://marupeke296.com/COL_2D_No7_EllipseVsEllipse.html の中に楕円の変倍を行っているルーチンがあるので、それを参考にしました。
変倍についても、詳しく解説されています。
楕円同士の衝突の判定は、片方の楕円が半径１の円になる様に変倍し、反対側の楕円の長径と、短径に１を加算し、１加算した楕円の式に、円側の中心位置の座標を、楕円上のＸ，Ｙ座標として入れて計算、計算の結果が１より大きいか小さいかで判定しています。
但し、衝突の計算については、問題があり、楕円の長径と、短径に同じを加算して行うのと、本来の衝突には誤差があり、長径と短径の比が大きくなると誤差が大きくなります。
誤差の方向は、衝突しているのに、衝突していないと判定をしてしまう方向です。
衝突の参照元の http://www.iis.sinica.edu.tw/JISE/1999/199901_09.pdf にも誤差について説明がなされています。
しかし、http://marupeke296.com/COL_2D_No7_EllipseVsEllipse.html では、ゲーム用の衝突判定のようなので、誤差は問題にならないでしょう。
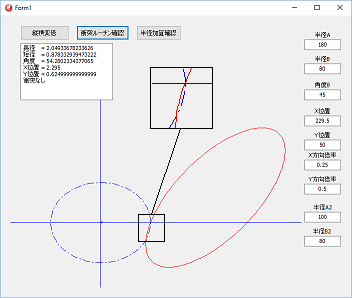
左図は、大きい楕円に対して、Ｘ方向０．２５倍、Ｙ方向０．５倍の変倍をした楕円をあらわしています。
元の頂点の位置を縦横違う変倍率で変倍すると、頂点の位置が変倍後の頂点の位置にならないことが、楕円の変倍の難しさとなっています。
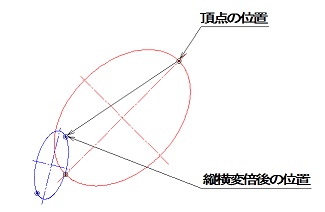
衝突判定について、どの様な判定なのか、図解してみました。
片方の楕円は、一点鎖線で傾きゼロの楕円です。
もう一方は赤の楕円ですが、判定は衝突をしているのに衝突無しとなっています。
ゲームのプログラムでは正確さより、演算速度が求められるので、これで問題ないでしょう。
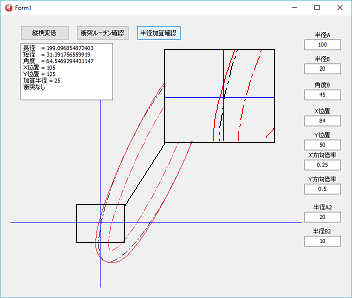衝突判定誤差は、長径と、短径の比が大きいほど大きくなります。
左図の黒の一点鎖線が赤の一点鎖線の楕円の長径と短径に、同じ値を加算した場合の楕円で、赤の実線の図形が、赤の一点鎖線の楕円の線に対して垂直方向に同じ値を加算した場合です。
青の縦横の線の交点の位置が、衝突判定の位置です、この位置と、黒の実線の楕円の線が重なった時が衝突判定ですが、本来の判定に必要な位置を表す赤の線に対して楕円中心寄りになっています。
楕円の線に対して垂直方向に同じ値を加算した形状の関数を導き出すことが出来ません。
この事が楕円の衝突の判定を難しくしています。
精度よく判定をする為には、楕円同士の交点を求める必要が出てきます。
衝突はさておき、楕円の縦横変倍は、全く問題ないので、衝突判定ルーチンから、変倍用ルーチンに変換したルーチンを作成してみました。
変倍について問題が無い事は、最小二乗法の楕円近似計算で確認しました。
楕円の座標を一定間隔の角度で計算し、X座標値と、Ｙ座標値をそれぞれの変倍率で変更し、最小二乗法により、楕円の各値を求めた結果、此処での計算と同じ値を得ることが出来ました。
type
TELLIPSE = record
fRad_X: double; // X 方向半径
fRad_Y: double; // Y 方向半径
fAngle: double; // 楕円角度
fCx : double; // 楕円中心位置 X
fcy : double; // 楕円中心位置 y
end;
//----------------------------------------------------------------
// 楕円の変倍ルーチン
// 参照 http://marupeke296.com/COL_2D_No7_EllipseVsEllipse.html
// 衝突ルーチンの中の変倍部分を利用して作成しました。
// 楕円 Ellipse 横倍率 XScale 縦倍率 YScale 戻り値 楕円
//----------------------------------------------------------------
function magnification(Ellipse: TELLIPSE; XScale, YScale: double): TELLIPSE;
var
nx, ny, px, py, ox, oy: double;
rx_pow2, ry_pow2: double;
A, B, C, D, E, F: double;
hk, h, k, th: double;
CosTh, SinTh, A_tt, B_tt: double;
KK, Rx_tt, Ry_tt: double;
begin
// XY スケール値に対する楕円変換係数設定
nx := 1 / XScale * cos(Ellipse.fAngle);
ny := 1 / XScale * sin(Ellipse.fAngle);
px := 1 / YScale * sin(Ellipse.fAngle);
py := 1 / YScale * cos(Ellipse.fAngle);
ox := cos(Ellipse.fAngle) * (- Ellipse.fCx) + sin(Ellipse.fAngle) * (- Ellipse.fCy);
oy := cos(Ellipse.fAngle) * (- Ellipse.fCy) - sin(Ellipse.fAngle) * (- Ellipse.fCx);
// 一般式 Ax^2 + By^2 + Cxy + Dx + Ey + F = 0
rx_pow2 := 1 / (Ellipse.fRad_X * Ellipse.fRad_X);
ry_pow2 := 1 / (Ellipse.fRad_Y * Ellipse.fRad_Y);
A := rx_pow2 * nx * nx + ry_pow2 * ny * ny;
B := rx_pow2 * px * px + ry_pow2 * py * py;
C := 2 * rx_pow2 * nx * px - 2 * ry_pow2 * ny * py;
D := 2 * rx_pow2 * nx * ox - 2 * ry_pow2 * ny * oy;
E := 2 * rx_pow2 * px * ox + 2 * ry_pow2 * py * oy;
F := (ox * ox * rx_pow2) + (oy * oy * ry_pow2) - 1;
// 楕円をゼロ度にする回転角度、原点に移動する移動量の計算
hk := 1 / (C * C - 4 * A * B);
h := (E * C - 2 * D * B) * hk; // X方向移動量
k := (D * C - 2 * A * E) * hk; // Y方向移動量
th := arctan2(C, B - A) / 2; // 回転角度
// 楕円の長径と短径計算
CosTh := cos(Th);
SinTh := sin(Th);
A_tt := A * CosTh * CosTh + B * SinTh * SinTh - C * CosTh * SinTh;
B_tt := A * SinTh * SinTh + B * CosTh * CosTh + C * CosTh * SinTh;
KK := - A * h * h - B * k * k - C * h * k + D * h + E * k - F;
if KK < 0 then KK := 0; // ルートの中の負数防止
Rx_tt := sqrt(KK / A_tt); // 半径a
Ry_tt := sqrt(KK / B_tt); // 半径b
result.fRad_X := Rx_tt;
result.fRad_Y := Ry_tt;
result.fAngle := -th; // 移動量なので符号を反転して位置に変更
result.fCx := -h;
result.fcy := -k;
end;
楕円弧の場合
楕円弧の場合、楕円の開始角度と、終了角度を指定しますが、楕円の開始点の座標Ｘs，Ｙs楕円の開始終了点の座標Ｘe，Ｙeを、それぞれ横変倍、縦変倍して角度に戻せば、新しい楕円の開始角と終了角を得ることが出来ます。
楕円弧の中心、楕円弧の開始点、終了点は、基準位置に対して変倍率分移動するだけなので、楕円の角度と違って単純に割り出すことが出来ます。
移動した新しい座標から、角度を逆算します。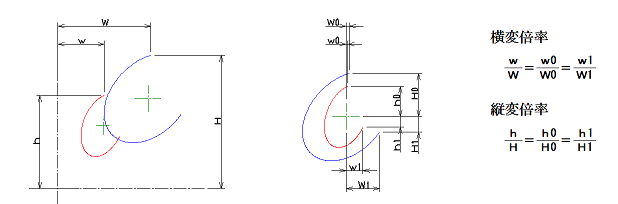
type
TELLIPSE = record
fRad_X : double; // X 方向半径
fRad_Y : double; // Y 方向半径
fAngle : double; // 楕円角度
fCx : double; // 楕円中心位置 X
fcy : double; // 楕円中心位置 Y
startAngle : double; // 開始角
endAngle : double; // 終了角
end;
//------------------------------------- // 変倍後の楕円の開始終了角の計算 // seAngle 楕円の開始終了角 // Angle 変倍前の楕円の角度 // XScale 横変倍率 // YScale 縦変倍率 // nAngle 変倍後の楕円の角度 //------------------------------------- function Start_End_Angle(seAngle, Angle, XScale, Yscale, nAngle: double): double; var x, y, ang: double; begin ang := seangle + Angle; // 角度 楕円の角度と開始終了角加算 x := cos(ang) * XScale; // 変倍X位置 長さを1としてＸ位置計算 y := sin(ang) * YScale; // 変倍Y位置 長さを1としてＹ位置計算 result := arctan2(y, x) - nAngle; // XYの位置から角度を計算し変倍後の楕円の角度を減算 if result < 0 then result := result + 2 * pi; if result > 2 * pi then result := result - 2 * pi; end; //---------------------------------------------------------------- // 楕円の変倍ルーチン // 参照 http://marupeke296.com/COL_2D_No7_EllipseVsEllipse.html // 衝突ルーチンの中の変倍部分を利用して作成しました。 // 楕円 Ellipse 横倍率 XScale 縦倍率 YScale 戻り値 楕円 //---------------------------------------------------------------- function magnification(Ellipse: TELLIPSE; XScale, YScale: double): TELLIPSE; var nx, ny, px, py, ox, oy: double; rx_pow2, ry_pow2: double; A, B, C, D, E, F: double; hk, h, k, th: double; CosTh, SinTh, A_tt, B_tt: double; KK, Rx_tt, Ry_tt: double; begin // XY スケール値に対する楕円変換係数設定 nx := 1 / XScale * cos(Ellipse.fAngle); ny := 1 / XScale * sin(Ellipse.fAngle); px := 1 / YScale * sin(Ellipse.fAngle); py := 1 / YScale * cos(Ellipse.fAngle); ox := cos(Ellipse.fAngle) * (- Ellipse.fCx) + sin(Ellipse.fAngle) * (- Ellipse.fCy); oy := cos(Ellipse.fAngle) * (- Ellipse.fCy) - sin(Ellipse.fAngle) * (- Ellipse.fCx); // 一般式 Ax^2 + By^2 + Cxy + Dx + Ey + F rx_pow2 := 1 / (Ellipse.fRad_X * Ellipse.fRad_X); ry_pow2 := 1 / (Ellipse.fRad_Y * Ellipse.fRad_Y); A := rx_pow2 * nx * nx + ry_pow2 * ny * ny; B := rx_pow2 * px * px + ry_pow2 * py * py; C := 2 * rx_pow2 * nx * px - 2 * ry_pow2 * ny * py; D := 2 * rx_pow2 * nx * ox - 2 * ry_pow2 * ny * oy; E := 2 * rx_pow2 * px * ox + 2 * ry_pow2 * py * oy; F := (ox * ox * rx_pow2) + (oy * oy * ry_pow2) - 1; // 楕円をゼロ度にする回転角度、原点に移動する移動量の計算 hk := 1 / (C * C - 4 * A * B); h := (E * C - 2 * D * B) * hk; // X方向移動量 k := (D * C - 2 * A * E) * hk; // Y方向移動量 th := arctan2(C, B - A) / 2; // 回転角度 // 楕円の長径と短径計算 CosTh := cos(Th); SinTh := sin(Th); A_tt := A * CosTh * CosTh + B * SinTh * SinTh - C * CosTh * SinTh; B_tt := A * SinTh * SinTh + B * CosTh * CosTh + C * CosTh * SinTh; KK := - A * h * h - B * k * k - C * h * k + D * h + E * k - F; if KK < 0 then KK := 0; // ルートの中の負数防止 Rx_tt := sqrt(KK / A_tt); // 半径a Ry_tt := sqrt(KK / B_tt); // 半径b // 開始角の計算 result.startAngle := Start_End_Angle(Ellipse.startAngle, Ellipse.fAngle, XScale, Yscale, -th); // 終了角の計算 result.endAngle := Start_End_Angle(Ellipse.EndAngle, Ellipse.fAngle, XScale, Yscale, -th); result.fRad_X := Rx_tt; result.fRad_Y := Ry_tt; result.fAngle := -th; // 移動量なので符号を反転して位置に変更 result.fCx := -h; result.fcy := -k; end;
プログラム全体
計算が正しいかどうかは、作図を行うのが一番なので、楕円の作図ルーチンを入れていますが、楕円の作図には結構沢山のルーチンを必用としているため、作図ルーチンの方が多くなっています。
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, system.Math, Vcl.StdCtrls, Vcl.ExtCtrls;
type
TELLIPSE = record
fRad_X : double; // X 方向半径
fRad_Y : double; // Y 方向半径
fAngle : double; // 楕円角度
fCx : double; // 楕円中心位置 X
fcy : double; // 楕円中心位置 Y
startAngle : double; // 開始角
endAngle : double; // 終了角
end;
type
TForm1 = class(TForm)
Button1: TButton;
Memo1: TMemo;
Button2: TButton;
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
LabeledEdit3: TLabeledEdit;
LabeledEdit4: TLabeledEdit;
LabeledEdit5: TLabeledEdit;
LabeledEdit6: TLabeledEdit;
LabeledEdit7: TLabeledEdit;
Image1: TImage;
Button3: TButton;
LabeledEdit8: TLabeledEdit;
LabeledEdit9: TLabeledEdit;
StartAngleEdit: TLabeledEdit;
EndAngleEdit: TLabeledEdit;
procedure Button1Click(Sender: TObject);
procedure Button2Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure Button3Click(Sender: TObject);
private
{ Private 宣言 }
function Dist(x1, y1, x2, y2 : double): double ;
function Angle(dx, dy: double): double ;
procedure LineSub(Tcv: TCanvas; px1, py1, px2, py2: double);
procedure pitchControl(NLine, LW: integer);
procedure LineSubPitch(Tcv : TCanvas; Ln: integer; var i: integer; var d1: double; px1, py1, px2, py2:double);
function angleSe(a, b, rad: double): double;
procedure EllipseExPlus(Tcv: TCanvas; lf, lw: integer; lc: Tcolor; a, b, x, y, rq, sq, eq, plus: double);
procedure EllipseEx(Tcv: TCanvas; lf, lw: integer; lc: Tcolor; a, b, x, y, rq, sq, eq: double);
function dataInput(var Ellipse0: TELLIPSE; var XScale, YScale: double): boolean;
procedure baseLine;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
const
PitchN = 5; // 線ピッチ設定数
LineN = 3; // 線種数
LIMIT8 = 0.00000001;
type
TLinePitch = Record // 線種用レコード
Pitch : array[0..PitchN] of double; // ピッチ 線長さ 空白の繰り返し
segment : integer; // ピッチ数
End;
var
LPitch : array of TLinePitch; // 線種用 (線ピッチ)
VPitch : array[0..PitchN] of double; // 線幅による線ピッチ設定用
lf : integer; // 線の種類
lw : integer; // 線の幅
//-----------------------------------------------
// 線幅によるピッチの補正
// 線幅を広くするとスペースが狭くなるので広げます
// NLine 線種
// LW 線幅
//-----------------------------------------------
procedure TForm1.pitchControl(NLine, LW: integer);
var
i : integer;
begin
// 線幅によるピッチの補正
for i := 0 to pitchN do begin
if i mod 2 <> 0 then // 奇数配列noセグメントがスペース
Vpitch[i] := LPitch[NLine].Pitch[i] + LW // スペースに線幅加算
else
Vpitch[i] := LPitch[NLine].Pitch[i];
end;
end;
//----------------------------
// 二点間線引き 実線
//----------------------------
procedure TForm1.LineSub(Tcv: TCanvas; px1, py1, px2, py2: double);
var
x1, y1, x2, y2 : integer ;
begin
x1 := Round(px1);
y1 := Round(py1);
x2 := Round(px2);
y2 := Round(py2);
Tcv.MoveTo(x1, y1);
Tcv.LineTo(x2, y2);
end;
//----------------------
// 距離（長さ）を計算
// x1, y1 : 始点
// x2, y2 : 終点
// out : 距離(長さ)
//----------------------
function TForm1.Dist(x1, y1, x2, y2 : double): double ;
begin
Result := Sqrt((x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1)) ;
end;
//--------------------------------
// 角度を計算[rad]
// dx : X方向差分
// dy : Y方向差分
// out: 角度 (0～2 * Pi)
//--------------------------------
function TForm1.Angle(dx, dy: double): double ;
var
r : double ;
begin
Result := 0.0;
if (Abs(dx) < LIMIT8) and (Abs(dy) < LIMIT8) then exit;
r := ArcTan2(dy, dx);
if r < 0.0 then r := r + 2.0 * Pi;
Result := r;
end;
//--------------------------------------
// 線分の表示・サブ２：線種指定
// Ln : 線種番号(1-)
// i : 開始セグメント番号(終了時更新)
// d1 : 開始ピッチ長さ (終了時更新)
// px1, py1 : 線分始点[mm]
// px2, py2 : 線分終点[mm]
//--------------------------------------
procedure TForm1.LineSubPitch(Tcv: TCanvas; Ln: integer; var i: integer; var d1: double; px1, py1, px2, py2:double);
var
x1, y1, x2, y2 : double;
a, sa, ca, d, p : double;
PenStyle : TPenstyle;
begin
PenStyle := Tcv.Pen.Style; // 線種バックアップ
Tcv.Pen.Style := psSolid;
if (Ln < 0) or (Ln >= LineN) then begin // 無い線種は実線
LineSub(Tcv, px1, py1, px2, py2);
Tcv.Pen.Style := PenStyle; // 線種戻し
exit;
end;
a := Angle(px2 - px1, py2 - py1); // 角度計算
d := Dist(px1, py1, px2, py2); // 距離計算
ca:= Cos(a); // コサイン
sa:= Sin(a); // サイン
x1:= px1; // 始点x
y1:= py1 ; // 始点y
repeat
p := Vpitch[i] - d1; // ピッチと開始ピッチ長さ差分 残り分
if (p > d) then p := d; // 距離より残り分が大きい場合 距離
x2 := x1 + p * ca ; // 新しい位置計算
y2 := y1 + p * sa ;
if (i mod 2) = 0 then // セグメント偶数毎に線引き 空白部線引きしない
LineSub(Tcv, x1, y1, x2, y2);
x1 := x2; // 終点を始点にセット
y1 := y2;
d := d - p ; // 残り長さ計算
if d > LIMIT8 then begin // 残り長さがあったら
d1 := 0.0; // 開始ピッチ長さクリア
Inc(i); // セグメントカウンターインクリメント
if i >= LPitch[Ln].segment then i := 0; // セグメント数を超えたらゼロに戻し
end;
until d <= LIMIT8;
d1 := d1 + p; // 開始ピッチ長さ
Tcv.Pen.Style := PenStyle; // 線種戻し
end;
//------------------------------------------
// 楕円の開始角を 基礎円の開始角に変換
//------------------------------------------
function TForm1.angleSe(a, b, rad: double): double;
const
KMIN = 0.00000001;
var
l : double;
begin
// 90°, 270°, 0°, 180° 360°近傍は計算しない
if (abs(rad - pi / 2) < KMIN) or (abs(rad - pi - pi / 2) < KMIN)
or (abs(rad) < KMIN) or (abs(rad - pi) < KMIN) or
(abs(rad - pi * 2) < KMIN)
then begin
result := rad;
exit;
end;
// 底辺の長さ計算 ( b / a の値がいつも正の値なので元の角度によって角度を補正)
// 分母がゼロに近くなる時もあるので、判別が不要なarctan2を使用します
l := b / a / tan(rad);
// 180°以下だったら
if rad < pi then
result := arctan2(1, l)
else
// 360°以下だったら
if rad < pi * 2 then
result := arctan2(1, l) + pi
// 360°を超えていたら
else
result := arctan2(1, l) + pi * 2;
end;
//-------------------------------------------------------------------------------
// 楕円Plusの描画 楕円面に対して直角に 距離plus を加算した位置をトレースします。
// 楕円面のカムフォロワの軌跡です。
//-------------------------------------------------------------------------------
procedure TForm1.EllipseExPlus(Tcv : TCanvas; lf, lw: integer; lc: Tcolor; a, b, x, y, rq, sq, eq, plus: double);
var
sqrad, eqrad : double;
qrad : double;
Ssqrad, Seqrad : double;
sp : integer;
dq : double;
d1 : double;
dp : integer;
xf, yf : double;
rdist, nrad : double;
px1, py1 : double;
px2, py2 : double;
i : integer;
xp, yp : double;
begin
Tcv.Pen.Width := lw;
Tcv.Pen.Color := lc;
// 線幅によるピッチの補正
pitchControl(lf, lw);
// 終了角と開始角が一致したら全周
if abs(sq - eq) < LIMIT8 then begin
sq := 0;
eq := 360;
end;
// 分割数 半径に応じて調整
sp := round(sqrt(a + b) * 4) * 2; // 分割数
// 楕円の計算と描画
sqrad := sq / 180 * pi;
eqrad := eq / 180 * pi;
qrad := pi / 180 * rq; // 回転角 ラジアン
Ssqrad := angleSe(a, b, sqrad); // 基本円角度に変換
Seqrad := angleSe(a, b, eqrad); // 基本円角度に変換
// 分割微小角計算 分割数角度で補正
if Seqrad >= Ssqrad then begin
sp := round(sp * (Seqrad - Ssqrad) / pi);
if sp = 0 then sp := 1;
dq := (Seqrad - Ssqrad) / sp // 分割微小角 ラジアン
end
else begin
sp := round(sp * (Pi * 2 - Ssqrad + Seqrad) / pi);
if sp = 0 then sp := 1;
dq := (Pi * 2 - Ssqrad + Seqrad) / sp; // 分割微小角 ラジアン
end;
// 開始点の計算
d1 := 0; // 長さ
dp := 0; // セグメント位置
xf := cos(Ssqrad) * a; // 基本楕円座標X スタート座標
yf := sin(Ssqrad) * b; // 基本楕円座標y スタート座標
xp := xf + b * cos(Ssqrad) / sqrt(a * a * sin(Ssqrad) * sin(Ssqrad)
+ b * b * cos(Ssqrad) * cos(Ssqrad)) * plus;
yp := yf + a * sin(Ssqrad) / sqrt(a * a * sin(Ssqrad) * sin(Ssqrad)
+ b * b * cos(Ssqrad) * cos(Ssqrad)) * plus;
nrad := arctan2(yp, xp) + qrad; // 新しい角度 回転角加算
rdist := sqrt(xp * xp + yp * yp); // 中心と楕円座標の距離
px1 := cos(nrad) * rdist + x; // 開始座標X
py1 := sin(nrad) * -rdist + y; // 開始座標Y -rdistはY座標反転の為
// WindowはY座標方向が逆のため
// 分割数分計算繰り返し描画
for i := 1 to sp do begin
xf := cos(Ssqrad + dq * i) * a;
yf := sin(Ssqrad + dq * i) * b;
xp := xf + b * cos(Ssqrad + dq * i) / sqrt(a * a * sin(Ssqrad + dq * i) * sin(Ssqrad + dq * i)
+ b * b * cos(Ssqrad + dq * i) * cos(Ssqrad + dq * i)) * plus;
yp := yf + a * sin(Ssqrad + dq * i) / sqrt(a * a * sin(Ssqrad + dq * i) * sin(Ssqrad + dq * i)
+ b * b * cos(Ssqrad + dq * i) * cos(Ssqrad + dq * i)) * plus;
nrad := arctan2(yp , xp) + qrad;
rdist := sqrt(xp * xp + yp * yp);
px2 := round(cos(nrad) * rdist + x); // 終点座標X
py2 := round(sin(nrad) * -rdist + y); // 終点座標Y
// ピッチ線描画
LineSubPitch( // ピッチ線描画
tcv, // TCanvas
lf, // 線種
dp, // セグメント位置
d1, // 長さ
px1, // 始点X
py1, // 始点Y
px2, // 終点X
py2 // 終点Y
);
px1 := px2; // 終点Xを始点Xに
py1 := py2; // 終点Yを始点Yに
end;
end;
//---------------------------------------
// 楕円の描画
//---------------------------------------
procedure TForm1.EllipseEx(Tcv : TCanvas; lf, lw: integer; lc: Tcolor; a, b, x, y, rq, sq, eq: double);
var
sqrad, eqrad : double;
qrad : double;
Ssqrad, Seqrad : double;
sp : integer;
dq : double;
d1 : double;
dp : integer;
xf, yf : double;
rdist, nrad : double;
px1, py1 : double;
px2, py2 : double;
i : integer;
begin
Tcv.Pen.Width := lw;
Tcv.Pen.Color := lc;
// 線幅によるピッチの補正
pitchControl(lf, lw);
// 終了角と開始角が一致したら全周
if abs(sq - eq) < LIMIT8 then begin
sq := 0;
eq := 360;
end;
// 分割数 半径に応じて調整
sp := round(sqrt(a + b) * 4); // 分割数
// 楕円の計算と描画
sqrad := sq / 180 * pi;
eqrad := eq / 180 * pi;
qrad := pi / 180 * rq; // 回転角 ラジアン
Ssqrad := angleSe(a, b, sqrad); // 基本円角度に変換
Seqrad := angleSe(a, b, eqrad); // 基本円角度に変換
// 分割微小角計算 分割数角度で補正
if Seqrad >= Ssqrad then begin
sp := round(sp * (Seqrad - Ssqrad) / pi);
if sp = 0 then sp := 1;
dq := (Seqrad - Ssqrad) / sp // 分割微小角 ラジアン
end
else begin
sp := round(sp * (Pi * 2 - Ssqrad + Seqrad) / pi);
if sp = 0 then sp := 1;
dq := (Pi * 2 - Ssqrad + Seqrad) / sp; // 分割微小角 ラジアン
end;
// 開始点の計算
d1 := 0; // 長さ
dp := 0; // セグメント位置
xf := cos(Ssqrad) * a; // 基本楕円座標X スタート座標
yf := sin(Ssqrad) * b; // 基本楕円座標y スタート座標
nrad := arctan2(yf, xf) + qrad; // 新しい角度 回転角加算
rdist := sqrt(xf * xf + yf * yf); // 中心と楕円座標の距離
px1 := cos(nrad) * rdist + x; // 開始座標X
py1 := sin(nrad) * -rdist + y; // 開始座標Y -rdistはY座標反転の為
// WindowはY座標方向が逆のため
// 分割数分計算繰り返し描画
for i := 1 to sp do begin
xf := cos(Ssqrad + dq * i) * a;
yf := sin(Ssqrad + dq * i) * b;
nrad := arctan2(yf , xf) + qrad;
rdist := sqrt(xf * xf + yf * yf);
px2 := round(cos(nrad) * rdist + x); // 終点座標X
py2 := round(sin(nrad) * -rdist + y); // 終点座標Y
// ピッチ線描画
LineSubPitch( // ピッチ線描画
tcv, // TCanvas
lf, // 線種
dp, // セグメント位置
d1, // 長さ
px1, // 始点X
py1, // 始点Y
px2, // 終点X
py2 // 終点Y
);
px1 := px2; // 終点Xを始点Xに
py1 := py2; // 終点Yを始点Yに
end;
end;
const
YL = 150; // 作図上のY基準位置
XL = 200; // 作図上のX基準位置
var
PlusF : boolean;
//------------------------------------------------------------------------
// 楕円E1 と楕円E2の衝突計算
// 参照 http://marupeke296.com/COL_2D_No7_EllipseVsEllipse.html
// 角度の計算以外は上記中のプログラムのまゝです
// 判定に誤差があり、半径方向同士以外は、衝突があっても無しと判定する
// 領域が存在します。
// 衝突判定 有りtrue 無し false
// 楕円の表示で、PlusF = Trueの時、半径加算の1を25相当に変換して表示
// 衝突判定は、楕円を原点に移動、角度をゼロとし、反対側の楕円中心の位置を
// 点座標として計算しています。
// 作図は、楕円の移動は行わず、反対側の楕円中心の位置を原点としています。
//------------------------------------------------------------------------
function CollisionEllipse(E1, E2: TELLIPSE): boolean;
var
//---------------------------------------------------------------------------
DefAng, Cos1, Sin1, nx, ny, px, py, ox, oy: double;
rx_pow2, ry_pow2, A, B, D, E, F, G: double;
tmp1, h, k, th : double;
CosTh, SinTh, A_tt, B_tt, KK, Rx_tt, Ry_tt, x_tt, y_tt, JudgeValue: double;
//---------------------------------------------------------------------------
TT, HH, Bysu: double;
begin
//---------------------------------------------------------------------------
// STEP1 : E2を単位円にする変換をE1に施す
DefAng := E1.fAngle-E2.fAngle;
Cos1 := cos( DefAng );
Sin1 := sin( DefAng );
nx := E2.fRad_X * Cos1;
ny := -E2.fRad_X * Sin1;
px := E2.fRad_Y * Sin1;
py := E2.fRad_Y * Cos1;
ox := cos( E1.fAngle )*(E2.fCx-E1.fCx) + sin(E1.fAngle)*(E2.fCy-E1.fCy);
oy := -sin( E1.fAngle )*(E2.fCx-E1.fCx) + cos(E1.fAngle)*(E2.fCy-E1.fCy);
// STEP2 : 一般式A～Gの算出
rx_pow2 := 1/(E1.fRad_X*E1.fRad_X);
ry_pow2 := 1/(E1.fRad_Y*E1.fRad_Y);
A := rx_pow2*nx*nx + ry_pow2*ny*ny;
B := rx_pow2*px*px + ry_pow2*py*py;
D := 2*rx_pow2*nx*px + 2*ry_pow2*ny*py;
E := 2*rx_pow2*nx*ox + 2*ry_pow2*ny*oy;
F := 2*rx_pow2*px*ox + 2*ry_pow2*py*oy;
G := (ox/E1.fRad_X)*(ox/E1.fRad_X) + (oy/E1.fRad_Y)*(oy/E1.fRad_Y) - 1;
// STEP3 : 平行移動量(h,k)及び回転角度θの算出
tmp1 := 1/(D*D-4*A*B);
h := (F*D-2*E*B)*tmp1;
k := (E*D-2*A*F)*tmp1;
th := arctan2(D, B - A) / 2;
// if (B-A) = 0 then th := 0
// else Th := arctan(D/(B-A)) * 0.5;
// STEP4 : +1楕円を元に戻した式で当たり判定
CosTh := cos(Th);
SinTh := sin(Th);
A_tt := A*CosTh*CosTh + B*SinTh*SinTh - D*CosTh*SinTh;
B_tt := A*SinTh*SinTh + B*CosTh*CosTh + D*CosTh*SinTh;
KK := A*h*h + B*k*k + D*h*k - E*h - F*k + G;
if(KK>0) then KK := 0; // 念のため
Rx_tt := 1+sqrt(-KK/A_tt);
Ry_tt := 1+sqrt(-KK/B_tt);
x_tt := CosTh*h-SinTh*k;
y_tt := SinTh*h+CosTh*k;
JudgeValue := x_tt*x_tt/(Rx_tt*Rx_tt) + y_tt*y_tt/(Ry_tt*Ry_tt);
if( JudgeValue <= 1 ) then
result:= true // 衝突
else
result:= false;
//-------------------------------------------------------------------------
// 結果の出力
// Bysuは衝突確認用楕円の半径が小さな値となるため大きく表示するための拡大率
// 入力された値をそのまま表示する場合は1とします。
Bysu := 1;
if PlusF then Bysu := 25;
with Form1 do begin
memo1.Clear;
memo1.Lines.Add('長径 = ' + floattostr((Rx_tt - 1) * Bysu));
memo1.Lines.Add('短径 = ' + floattostr((Ry_tt - 1) * Bysu));
memo1.Lines.Add('角度 = ' + floattostr(- th / pi * 180));
memo1.Lines.Add('Ｘ位置 = ' + floattostr(- h * Bysu));
memo1.Lines.Add('Ｙ位置 = ' + floattostr(- k * Bysu));
if PlusF then
memo1.Lines.Add('加算半径 = ' + floattostr(Bysu));
TT := Form1.ClientHeight - YL + K * Bysu;
HH := XL - h * Bysu;
lf := 1; // 線種一点鎖線
lw := 1; // 線幅１
// 半径加算確認
if PlusF then begin
EllipseEx( // 楕円作図
Image1.Canvas, // TCanvas
lf, // 線種
lw, // 線幅
clred, // 線の色
(Rx_tt - 1) * Bysu, // 半径 a 加算無し
(Ry_tt - 1) * Bysu, // 半径 b 加算無し
HH, // 中心座標 X
TT, // 中心座標 Y
- th / pi * 180, // 回転角
0, // 始角
360 // 終角
);
EllipseEx( // 楕円作図
Image1.Canvas, // TCanvas
lf, // 線種
lw, // 線幅
clblack, // 線の色
(Rx_tt) * Bysu, // 半径 a 加算あり
(Ry_tt) * Bysu, // 半径 b 加算あり
HH, // 中心座標 X
TT, // 中心座標 Y
- th / pi * 180, // 回転角
0, // 始角
360 // 終角
);
lf := 3; // 線種実線
EllipseExplus( // 楕円作図 楕円曲線に対して垂直にBysuを加算
Image1.Canvas, // TCanvas
lf, // 線種
lw, // 線幅
clred, // 線の色
(Rx_tt - 1) * Bysu, // 半径 a 加算無し
(Ry_tt - 1) * Bysu, // 半径 b 加算無し
HH, // 中心座標 X
TT, // 中心座標 Y
- th / pi * 180, // 回転角
0, // 始角
360, // 終角
Bysu);
end;
// 衝突確認
if not PlusF then begin
TT := Form1.ClientHeight - YL;
HH := XL;
EllipseEx( // 楕円作図
Image1.Canvas, // TCanvas
lf, // 線種
lw, // 線幅
clblue, // 線の色
E2.fRad_X, // 半径 a
E2.fRad_Y, // 半径 b
HH, // 中心座標 X
TT, // 中心座標 Y
E2.fAngle / pi * 180, // 回転角
0, // 始角
360 // 終角
);
end;
end;
end;
//-------------------------------------
// 変倍後の楕円の開始終了角の計算
// seAngle 楕円の開始終了角
// Angle 変倍前の楕円の角度
// XScale 横変倍率
// YScale 縦変倍率
// nAngle 変倍後の楕円の角度
//-------------------------------------
function Start_End_Angle(seAngle, Angle, XScale, Yscale, nAngle: double): double;
var
x, y, ang: double;
begin
ang := seangle + Angle; // 角度 楕円の角度と開始終了角加算
x := cos(ang) * XScale; // 変倍X位置 長さを1としてＸ位置計算
y := sin(ang) * YScale; // 変倍Y位置 長さを1としてＹ位置計算
result := arctan2(y, x) - nAngle; // XYの位置から角度を計算し変倍後の楕円の角度を減算
if result < 0 then result := result + 2 * pi;
if result > 2 * pi then result := result - 2 * pi;
end;
//----------------------------------------------------------------
// 楕円の変倍ルーチン
// 参照 http://marupeke296.com/COL_2D_No7_EllipseVsEllipse.html
// 衝突ルーチンの中の変倍部分を利用して作成しました。
// 楕円 Ellipse 横倍率 XScale 縦倍率 YScale 戻り値 楕円
//----------------------------------------------------------------
function magnification(Ellipse: TELLIPSE; XScale, YScale: double): TELLIPSE;
var
nx, ny, px, py, ox, oy: double;
rx_pow2, ry_pow2: double;
A, B, C, D, E, F: double;
hk, h, k, th: double;
CosTh, SinTh, A_tt, B_tt: double;
KK, Rx_tt, Ry_tt: double;
begin
// XY スケール値に対する楕円変換係数設定
nx := 1 / XScale * cos(Ellipse.fAngle);
ny := 1 / XScale * sin(Ellipse.fAngle);
px := 1 / YScale * sin(Ellipse.fAngle);
py := 1 / YScale * cos(Ellipse.fAngle);
ox := cos(Ellipse.fAngle) * (- Ellipse.fCx) + sin(Ellipse.fAngle) * (- Ellipse.fCy);
oy := cos(Ellipse.fAngle) * (- Ellipse.fCy) - sin(Ellipse.fAngle) * (- Ellipse.fCx);
// 一般式 Ax^2 + By^2 + Cxy + Dx + Ey + F
rx_pow2 := 1 / (Ellipse.fRad_X * Ellipse.fRad_X);
ry_pow2 := 1 / (Ellipse.fRad_Y * Ellipse.fRad_Y);
A := rx_pow2 * nx * nx + ry_pow2 * ny * ny;
B := rx_pow2 * px * px + ry_pow2 * py * py;
C := 2 * rx_pow2 * nx * px - 2 * ry_pow2 * ny * py;
D := 2 * rx_pow2 * nx * ox - 2 * ry_pow2 * ny * oy;
E := 2 * rx_pow2 * px * ox + 2 * ry_pow2 * py * oy;
F := (ox * ox * rx_pow2) + (oy * oy * ry_pow2) - 1;
// 楕円をゼロ度にする回転角度、原点に移動する移動量の計算
hk := 1 / (C * C - 4 * A * B);
h := (E * C - 2 * D * B) * hk; // X方向移動量
k := (D * C - 2 * A * E) * hk; // Y方向移動量
th := arctan2(C, B - A) / 2; // 回転角度
// 楕円の長径と短径計算
CosTh := cos(Th);
SinTh := sin(Th);
A_tt := A * CosTh * CosTh + B * SinTh * SinTh - C * CosTh * SinTh;
B_tt := A * SinTh * SinTh + B * CosTh * CosTh + C * CosTh * SinTh;
KK := - A * h * h - B * k * k - C * h * k + D * h + E * k - F;
if KK < 0 then KK := 0; // ルートの中の負数防止
Rx_tt := sqrt(KK / A_tt); // 半径a
Ry_tt := sqrt(KK / B_tt); // 半径b
// 開始角の計算
result.startAngle := Start_End_Angle(Ellipse.startAngle, Ellipse.fAngle, XScale, Yscale, -th);
// 終了角の計算
result.endAngle := Start_End_Angle(Ellipse.endAngle, Ellipse.fAngle, XScale, Yscale, -th);
result.fRad_X := Rx_tt;
result.fRad_Y := Ry_tt;
result.fAngle := -th; // 移動量なので符号を反転して位置に変更
result.fCx := -h;
result.fcy := -k;
end;
//--------------------------------------------------
// 入力データーの処理
//--------------------------------------------------
function TForm1.dataInput(var Ellipse0: TELLIPSE; var XScale, YScale: double): boolean;
var
ch : integer;
Rect : TRect;
begin
// 画像消去
Result := False;
val(LabeledEdit1.Text, Ellipse0.fRad_X, ch);
if (ch <> 0) or (Ellipse0.fRad_X <= 0) then begin
application.MessageBox('入力に間違いがあります','半径 Ａ', 0);
exit;
end;
val(LabeledEdit2.Text, Ellipse0.fRad_Y, ch);
if (ch <> 0) or (Ellipse0.fRad_Y <= 0) then begin
application.MessageBox('入力に間違いがあります','半径 Ｂ', 0);
exit;
end;
val(LabeledEdit3.Text, Ellipse0.fAngle, ch);
if ch <> 0 then begin
application.MessageBox('入力に間違いがあります','角度', 0);
exit;
end;
val(LabeledEdit4.Text, Ellipse0.fCx, ch);
if ch <> 0 then begin
application.MessageBox('入力に間違いがあります','Ｘ位置', 0);
exit;
end;
val(LabeledEdit5.Text, Ellipse0.fcy, ch);
if ch <> 0 then begin
application.MessageBox('入力に間違いがあります','Ｙ位置', 0);
exit;
end;
val(StartAngleEdit.Text, Ellipse0.startAngle, ch);
if ch <> 0 then begin
application.MessageBox('入力に間違いがあります','開始角', 0);
exit;
end;
repeat
if Ellipse0.startAngle < 0 then Ellipse0.startAngle := Ellipse0.startAngle + 360;
until Ellipse0.startAngle >= 0;
val(EndAngleEdit.Text, Ellipse0.EndAngle, ch);
if ch <> 0 then begin
application.MessageBox('入力に間違いがあります','開始角', 0);
exit;
end;
repeat
if Ellipse0.endAngle > 360 then Ellipse0.endAngle := Ellipse0.endAngle - 360;
until Ellipse0.endAngle <= 360;
val(LabeledEdit6.Text, XScale, ch);
if (ch <> 0) or (XScale <= 0) then begin
application.MessageBox('入力に間違いがあります','Ｘ方向倍率', 0);
exit;
end;
val(LabeledEdit7.Text, YScale, ch);
if (ch <> 0) or (YScale <= 0) then begin
application.MessageBox('入力に間違いがあります','Ｙ方向倍率', 0);
exit;
end;
Rect.Top := 0;
Rect.Left := 0;
Rect.Right := Image1.Width;
Rect.Bottom := Image1.Height;
Image1.Canvas.Brush.Style := bsSolid;
Image1.canvas.Brush.Color := clBtnface;
Image1.canvas.FillRect(Rect);
Result := True;
end;
//--------------------------------------
// 基準位置の線引
//--------------------------------------
procedure TForm1.baseLine;
begin
Image1.Canvas.Pen.Style := psSolid;
Image1.Canvas.Pen.Width := 1;
Image1.Canvas.Pen.Color := clBlue;
Image1.Canvas.MoveTo(20, ClientHeight - YL);
Image1.Canvas.LineTo(ClientWidth - 100, ClientHeight - YL);
Image1.Canvas.MoveTo(XL, 100);
Image1.Canvas.LineTo(XL, ClientHeight - 20);
end;
//----------------------------------
// 縦横変倍
//----------------------------------
procedure TForm1.Button1Click(Sender: TObject);
var
Ellipse1, Ellipse2: TELLIPSE;
Xsc, Ysc: double;
TT, HH: double;
begin
if not dataInput(Ellipse1, Xsc, Ysc) then exit;
Ellipse1.fAngle := Ellipse1.fAngle / 180 * pi;
Ellipse1.startAngle := Ellipse1.startAngle / 180 * pi;
Ellipse1.endAngle := Ellipse1.endAngle / 180 * pi;
Ellipse2 := magnification(Ellipse1, Xsc, Ysc);
memo1.Clear;
memo1.Lines.Add('長径 = ' + floattostr(Ellipse2.fRad_X));
memo1.Lines.Add('短径 = ' + floattostr(Ellipse2.fRad_Y));
memo1.Lines.Add('角度 = ' + floattostr(Ellipse2.fAngle / pi * 180));
memo1.Lines.Add('Ｘ位置 = ' + floattostr(Ellipse2.fCx));
memo1.Lines.Add('Ｙ位置 = ' + floattostr(Ellipse2.fCy));
memo1.Lines.Add('開始角度 = ' + floattostrF(Ellipse2.startAngle / pi * 180, ffFixed, 8, 2) + '°');
memo1.Lines.Add('終了角度 = ' + floattostrF(Ellipse2.endAngle / pi * 180, ffFixed, 8, 2) + '°');
TT := Form1.ClientHeight - YL - Ellipse1.fCy;
HH := XL + Ellipse1.fCx;
lf := 3;
lw := 1;
EllipseEx( // 楕円作図
Image1.Canvas, // TCanvas
lf, // 線種
lw, // 線幅
clred, // 線の色
Ellipse1.fRad_X, // 半径 a
Ellipse1.fRad_Y, // 半径 b
HH, // 中心座標 X
TT, // 中心座標 Y
Ellipse1.fAngle / pi * 180, // 回転角
Ellipse1.startAngle / pi * 180, // 始角
Ellipse1.endAngle / pi * 180 // 終角
);
TT := ClientHeight - YL - Ellipse2.fCy;
HH := XL + Ellipse2.fCx;
lf := 1;
lw := 1;
EllipseEx( // 楕円作図
Image1.Canvas, // TCanvas
lf, // 線種
lw, // 線幅
clred, // 線の色
Ellipse2.fRad_X, // 半径 a
Ellipse2.fRad_Y, // 半径 b
HH, // 中心座標 X
TT, // 中心座標 Y
Ellipse2.fAngle / pi * 180, // 回転角
Ellipse2.startAngle / pi * 180, // 始角
Ellipse2.endAngle / pi * 180 // 終角
);
baseLine;
end;
//-----------------------------------------------
// 変倍率を逆数にして半径に変換
// 楕円同士の衝突計算 あくまでもおおよそ
// 判定誤差あり
//-----------------------------------------------
procedure TForm1.Button2Click(Sender: TObject);
var
Ellipse1, Ellipse2: TELLIPSE;
Xsc, Ysc: double;
TT, HH: double;
Ch : integer;
begin
if not dataInput(Ellipse1, Xsc, Ysc) then exit;
plusF := False;
Ellipse1.fAngle := Ellipse1.fAngle / 180 * pi;
val(LabeledEdit8.Text, Ellipse2.fRad_X, ch);
if (ch <> 0) or (Ellipse2.fRad_X <= 0) then begin
application.MessageBox('入力に間違いがあります','半径 Ａ2', 0);
exit;
end;
val(LabeledEdit9.Text, Ellipse2.fRad_Y, ch);
if (ch <> 0) or (Ellipse2.fRad_Y <= 0) then begin
application.MessageBox('入力に間違いがあります','半径 Ｂ2', 0);
exit;
end;
Ellipse2.fAngle := 0 / 180 * pi;
Ellipse2.fCx := 0;
Ellipse2.fcy := 0;
Ellipse2.startAngle := 0;
Ellipse2.endAngle := 0;
if CollisionEllipse(Ellipse1, Ellipse2) then
memo1.Lines.Add('衝突')
else
memo1.Lines.Add('衝突なし');
TT := Form1.ClientHeight - YL - Ellipse1.fCy;
HH := XL + Ellipse1.fCx;
lf := 3;
lw := 1;
EllipseEx( // 楕円作図
Image1.Canvas, // TCanvas
lf, // 線種
lw, // 線幅
clred, // 線の色
Ellipse1.fRad_X, // 半径 a
Ellipse1.fRad_Y, // 半径 b
HH, // 中心座標 X
TT, // 中心座標 Y
Ellipse1.fAngle / pi * 180, // 回転角
0, // 始角
360 // 終角
);
baseLine;
end;
//----------------------------------------------------
// 楕円の長径と短径に同じ値を加算した場合と
// 楕円面に直角方向に同じ値を加算した場合の軌跡の作図
//----------------------------------------------------
procedure TForm1.Button3Click(Sender: TObject);
var
Ellipse1, Ellipse2: TELLIPSE;
Xsc, Ysc: double;
// TT, HH: double;
Ch : integer;
begin
if not dataInput(Ellipse1, Xsc, Ysc) then exit;
Ellipse1.fAngle := Ellipse1.fAngle / 180 * pi;
val(LabeledEdit8.Text, Ellipse2.fRad_X, ch);
if (ch <> 0) or (Ellipse2.fRad_X <= 0) then begin
application.MessageBox('入力に間違いがあります','半径 Ａ2', 0);
exit;
end;
val(LabeledEdit9.Text, Ellipse2.fRad_Y, ch);
if (ch <> 0) or (Ellipse2.fRad_Y <= 0) then begin
application.MessageBox('入力に間違いがあります','半径 Ｂ2', 0);
exit;
end;
Ellipse2.fAngle := 0 / 180 * pi;
Ellipse2.fCx := 0;
Ellipse2.fcy := 0;
plusF := True;
if CollisionEllipse(Ellipse1, Ellipse2) then
memo1.Lines.Add('衝突')
else
memo1.Lines.Add('衝突なし');
baseLine;
end;
// 初期設定
procedure TForm1.FormCreate(Sender: TObject);
begin
top := (Screen.Height - height) div 2;
left := (Screen.Width - Width) div 2;
// 線種配列确保
setlength(LPitch, LineN);
// 線種データーセット
LPitch[0].segment := 2; // 破線
LPitch[0].Pitch[0] := 6;
LPitch[0].Pitch[1] := 3;
LPitch[1].segment := 4; // １点鎖線
LPitch[1].Pitch[0] := 15;
LPitch[1].Pitch[1] := 3;
LPitch[1].Pitch[2] := 3;
LPitch[1].Pitch[3] := 3;
LPitch[2].segment := 6; // ２点鎖線
LPitch[2].Pitch[0] := 18;
LPitch[2].Pitch[1] := 3;
LPitch[2].Pitch[2] := 3;
LPitch[2].Pitch[3] := 3;
LPitch[2].Pitch[4] := 3;
LPitch[2].Pitch[5] := 3;
end;
end.
Ellipse_magnification.zip