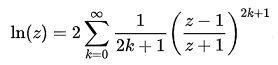
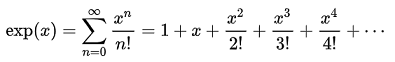
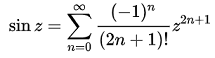
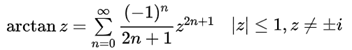
ガウスの超幾何関数をBigdecimal、Bigintegerのみで計算する為の、複素数関数
ガウスの超幾何関数の多倍長計算にMPArithとBigdecimal、Bigintegerを使用していましたが、Bigdecimal、Bigintegerのみ使用してプログラムを作成するために、必要な、関数を用意することにしました。
複素数の四則演算を除き
特に必要なものは、
ln、exp、power、sin, arctan
です。
演算は級数を利用して行います。
一般的な級数を使用すると演算は遅いのですが、多用するわけでは無いので、問題はないてす。
arctanに関しては、arg(複素数の角度)の計算に使用されるだけなので、実数の計算でも可能です。
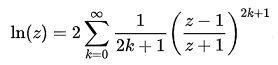
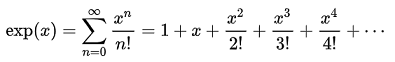
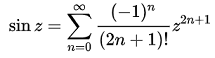
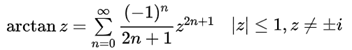
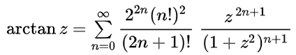レオンハルト・オイラーの計算式
powerの計算はxy、exp(ln(x)*y)
となりますが、条件によって、実数値、又は虚数値がゼロに成るべき値が演算誤差によりゼロにならないので、ｘとyの値からゼロに補正しています。
arctanの計算は、複素数は必要ないのですが、一応作成してみました。
arctanの計算は、一般の級数とレオンハルト・オイラーの級数を作成し、どれ位、レオンハルト・オイラーの級数の計算が早くなるかの確認用に作成しました。
また、レオンハルト・オイラーの計算でないと、arctan(1)の計算が出来ませんし、1近傍の計算に時間がかかります。
プログラム
unit main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, system.Math, System.VarCmplx, Vcl.StdCtrls, Vcl.Imaging.pngimage, Vcl.ExtCtrls, Velthuis.BigIntegers, Velthuis.Bigdecimals; type // 複素数構造体 CBig = record r : bigdecimal; i : bigdecimal; end; TForm1 = class(TForm) zEdit: TLabeledEdit; Memo1: TMemo; epsEdit: TLabeledEdit; yEdit: TLabeledEdit; yiEdit: TLabeledEdit; Image1: TImage; Button1: TButton; CheckBox1: TCheckBox; CheckBox2: TCheckBox; iedit: TLabeledEdit; procedure Button1Click(Sender: TObject); procedure epsEditChange(Sender: TObject); private { Private 宣言 } public { Public 宣言 } end; var Form1: TForm1; implementation {$R *.dfm} // CBig複素数の加算 function cadd(a, b: CBig): CBig; begin result.r := a.r + b.r; result.i := a.i + b.i; end; // CBig複素数の減算 function csub(a, b: CBig): CBig; begin result.r := a.r - b.r; result.i := a.i - b.i; end; // Cbig複素数の乗算 function cmul(a, b: Cbig): CBig; begin result.r := a.r * b.r - a.i * b.i; result.i := a.r * b.i + a.i * b.r; end; // Cbig複素数の除算 function cdiv(a, b: Cbig): Cbig; var bb, arbraibi, aibrarbi: Bigdecimal; dpcs : integer; begin dpcs := bigdecimal.DefaultPrecision; bb := b.r * b.r + b.i * b.i; arbraibi := a.r * b.r + a.i * b.i; aibrarbi := a.i * b.r - a.r * b.i; bb := bb.RoundToPrecision(dpcs); arbraibi := arbraibi.RoundToPrecision(dpcs); aibrarbi := aibrarbi.RoundToPrecision(dpcs); if bb <> Bigdecimal.Zero then begin result.r := arbraibi / bb; result.i := aibrarbi / bb; end else begin result.r := Bigdecimal.Zero; result.i := Bigdecimal.Zero; end; end; // Cbigの絶対値 function cabs(a : cbig; dpcs : integer): bigdecimal; var arh2, aih2 : bigdecimal; tmp : bigdecimal; begin arh2 := a.r * a.r; aih2 := a.i * a.i; tmp := arh2 + aih2; result := bigdecimal.Sqrt(tmp, dpcs); end; // Comp/deci function cdivdec(a: Cbig; b: bigdecimal): cbig; begin result.r := a.r / b; result.i := a.i / b; end; // exp(x) function exp_big(x: Cbig; dpcs: integer; eps : bigdecimal): Cbig; var xh, s, sb, si, i, ih, ss: Cbig; one, two ,ass : bigdecimal; begin one := bigdecimal.One; two := bigdecimal.Two; two := two + two + two + two; two := two.RoundToPrecision(dpcs); i.r := One; i.i := bigdecimal.Zero; ih := i; x.r := x.r.RoundToPrecision(dpcs); x.i := x.i.RoundToPrecision(dpcs); x.r := x.r / two; x.i := x.i / two; xh := x; s := x; repeat sb := s; i.r := i.r + one; ih := cmul(ih, i); // i! xh := cmul(xh, x); // x^n xh.r := xh.r.RoundToPrecision(dpcs); xh.i := xh.i.RoundToPrecision(dpcs); si := cdiv(xh, ih); // x^n/i! s := cadd(s, si); ss := csub(s, sb); ass := cabs(ss, dpcs); until (ass < eps); form1.Memo1.Lines.Append('exp n= ' + i.r.ToString); s.r := s.r + one; s := cmul(s, s); s := cmul(s, s); result := cmul(s, s); result.r := result.r.RoundToPrecision(dpcs); result.i := result.i.RoundToPrecision(dpcs); end; // π // https://www.kurims.kyoto-u.ac.jp/~ooura/pi_fft-j.html // T.Ooura AGM アルゴリズ function pi_big: Bigdecimal; var n, dpcs, pcsBack : integer; rmback : BigDecimal.RoundingMode; SQRT_SQRT_EPSILON, c, b, e : BigDecimal; npow : Bigdecimal; a, one, two, four, five, eight : Bigdecimal; begin pcsBack := BigDecimal.DefaultPrecision; // 除算演算精度バックアップ rmBack := BigDecimal.DefaultRoundingMode; // 除算丸めモードバックアップ dpcs := pcsBack + 5; // 指定精度 + α BigDecimal.DefaultPrecision := dpcs; BigDecimal.DefaultRoundingMode := rmNearesteven; one := '1'; one := one.RoundToPrecision(dpcs); // oneの有効桁数をdpcsに設定 two := '2'; four := '4'; five := '5'; eight := '8'; SQRT_SQRT_EPSILON := one / BigDecimal.IntPower(two, dpcs shl 0); // 収束判定値 c := BigDecimal.Sqrt(one / eight, dpcs * 2); a := one + c + c + c; b := BigDecimal.Sqrt(a, dpcs * 2); e := b - five / eight; b := b + b; c := e - c; a := a + e; npow := '4'; n := 0; while (e > SQRT_SQRT_EPSILON) and (n < 100) do begin npow := npow + npow; e := (a + b) / two; // 平均値 除算有効桁数での丸め b := a * b; b := b.RoundToPrecision(dpcs); // pcs + α 丸め b := BigDecimal.Sqrt(b, dpcs * 2); // 平方根有効桁数での丸め e := e - b; b := b + b; c := c - e; a := e + b; inc(n); end; e := e * e; e := e.RoundToPrecision(dpcs); // pcs + α 丸め e := e / four; // e = e * e / 4 a := a + b; result := (a * a - e - e / two) / (a * c - e) / npow; // 除算の順番に注意 result := result.RoundToPrecision(pcsBack); // 指定の精度に丸め BigDecimal.DefaultPrecision := pcsBack; // 除算演算精度復帰 BigDecimal.DefaultRoundingMode := rmBack; // 除算丸めモード復帰 end; // variant double 計算 // Ln(z) = 2arctanh{(z-1)/z+1)} 対数計算 function lnd(dz, di : double): variant; var zi: variant; c10, c10c : variant; pc, mc : integer; max : double; argf : boolean; begin result := varascomplex(result); c10 := varascomplex(c10); c10c := varascomplex(c10c); zi := varascomplex(zi); c10.real := 10; c10.Imaginary := 0; c10c := 2 * VarComplexArcTanH((c10 - 1) / (c10 + 1)); // len(10+0i) zi.real := dz; zi.Imaginary := di; max := VarComplexAbs(zi); // 絶対値 pc := 0; mc := 0; repeat if max >= 10 then begin max := max / 10; zi.real := zi.real / 10; zi.Imaginary := zi.Imaginary / 10; inc(pc); end; if max < 1 then begin max := max * 10; zi.real := zi.real * 10; zi.Imaginary := zi.Imaginary * 10; inc(mc); end; until (max < 10) and (max >= 1); // real < 0 の時 分母がゼロになり計算出来ない事があるので符号を反転します。 argf := false; if zi.real < 0 then begin zi.real := -zi.real; zi.Imaginary := -zi.Imaginary; argf := true; end; result := 2 * VarComplexArcTanH((zi - 1) / (zi + 1)); if pc > 0 then result.real := result.real + c10c * pc; if mc > 0 then result.real := result.real - c10c * mc; // real < 0 時符号を反転して計算しているので虚数部にπを加算して補正します。 if argf then result.Imaginary := result.Imaginary + pi; end; // sin(z); function sin_big(z : Cbig; eps : bigdecimal; dpcs: integer): Cbig; var fa2n1, fn, zh2n1, zh2: cbig; cone, s, tmp : cbig; abss: bigdecimal; FG : boolean; n : integer; begin n := 0; // n = 0 cone.r := bigdecimal.One; cone.i := bigdecimal.Zero; zh2n1 := z; // z^(2n+1) zh2 := cmul(z,z); // z^2 fa2n1 := cone; //(2n+1)! fn := cone; // (2*0+1)! s := z; // z FG := false; // n = 1 ～ repeat zh2n1 := cmul(zh2n1, zh2); // z^(2n+1) fn := cadd(fn, cone) ; // fn = fn + 1 fa2n1 := cmul(fa2n1, fn); fn := cadd(fn, cone) ; fa2n1 := cmul(fa2n1, fn); // (2n+1)! fa2n1.r := fa2n1.r.RoundToPrecision(dpcs); fa2n1.i := fa2n1.i.RoundToPrecision(dpcs); zh2n1.r := zh2n1.r.RoundToPrecision(dpcs); zh2n1.i := zh2n1.i.RoundToPrecision(dpcs); tmp := cdiv(zh2n1, fa2n1); // z^(2n+1) / (2n+1)! if FG then begin s := cadd(s, tmp); FG := false; end else begin s := csub(s, tmp); FG := true; end; inc(n); abss := cabs(tmp, dpcs); until abss < eps; form1.Memo1.Lines.Append(' sin n= ' + intTostr(n)); result := s; end; // arctan(z) // 1 を越えたら反対側の角度を計算 function arctan_big(z: cbig; eps : bigdecimal; dpcs: integer): cbig; var cone, s, z2, z2n, pi2, tmp: cbig; absz, abst, nbig : bigdecimal; n : integer; begin if (z.r = bigdecimal.Zero) and (z.i = bigdecimal.One) then begin result.r := bigdecimal.Zero; result.i := bigdecimal.Zero; exit; end; cone.r := bigdecimal.One; cone.i := bigdecimal.Zero; n := 0; absz := cabs(z, dpcs); if absz > bigdecimal.One then begin z.r := z.r.RoundToPrecision(dpcs); z.i := z.i.RoundToPrecision(dpcs); cone.r := cone.r.RoundToPrecision(dpcs); cone.i := cone.i.RoundToPrecision(dpcs); z := cdiv(cone, z); end; z2 := cmul(z, z); z2.r := z2.r.RoundToPrecision(dpcs); z2.i := z2.i.RoundToPrecision(dpcs); s := z; z2n := z; nbig := bigdecimal.One + bigdecimal.Two; // z2 := -z2; z2.r := -z2.r; z2.i := -z2.i; repeat z2n := cmul(z2n, z2); z2n.r := z2n.r.RoundToPrecision(dpcs); z2n.i := z2n.i.RoundToPrecision(dpcs); nbig := nbig.RoundToPrecision(dpcs); tmp := cdivdec(z2n, nbig); s := cadd(s, tmp); abst := cabs(tmp, dpcs); nbig := nbig + bigdecimal.Two; inc(n); until (abst <= eps) or (n > 20000); if absz > bigdecimal.One then begin pi2.r := pi_big; pi2.i := bigdecimal.Zero; pi2.r := pi2.r / bigdecimal.Two; // π/2 s := csub(pi2, s); end; form1.Memo1.Lines.Append(' arctan n= ' + intTostr(n)); result := s; end; // arctan // 1 を越えたら反対側の角度を計算 // レオンハルト・オイラーの計算 function arctan_Leonhard_Euler(x: cbig; eps : bigdecimal; dpcs: integer): cbig; var n : integer; ax, ax2, y, ans, bans, f, cone, i, tmp, tmpy : cbig; absz, abst : bigdecimal; begin if (x.r = bigdecimal.Zero) and (x.i = bigdecimal.One) then begin result.r := bigdecimal.Zero; result.i := bigdecimal.Zero; exit; end; ax := x; cone.r := bigdecimal.One; cone.i := bigdecimal.Zero; absz := cabs(ax, dpcs); if absz > bigdecimal.One then begin ax.r := ax.r.RoundToPrecision(dpcs); ax.i := ax.i.RoundToPrecision(dpcs); cone.r := cone.r.RoundToPrecision(dpcs); cone.i := cone.i.RoundToPrecision(dpcs); ax := cdiv(cone, ax); end; ax2 := cmul(ax, ax); tmp := cadd(ax2, cone); ax2.r := ax2.r.RoundToPrecision(dpcs); ax2.i := ax2.i.RoundToPrecision(dpcs); tmp.r := tmp.r.RoundToPrecision(dpcs); tmp.i := tmp.i.RoundToPrecision(dpcs); y := cdiv(ax2, tmp); i := cone; ans := cone; f := cone; tmpy.r := bigdecimal.Zero; tmpy.i := bigdecimal.Zero; n := 0; repeat bans := ans; tmp := cmul(f, i); // f * i tmp.r := tmp.r * bigdecimal.Two; // f * i * 2 tmp.i := tmp.i * bigdecimal.Two; tmpy.r := (i.r + i.r) + bigdecimal.One; // i * 2 + 1 tmp.r := tmp.r.RoundToPrecision(dpcs); tmp.i := tmp.i.RoundToPrecision(dpcs); tmpy.r := tmpy.r.RoundToPrecision(dpcs); tmp := cdivdec(tmp, tmpy.r); f := cmul(tmp, y); // f := f * i * 2 / (i * 2 + 1) * y; ans := cadd(ans, f); i.r := i.r + bigdecimal.One; inc(n); abst := cabs(f, dpcs); until (abst < eps) or (n > 10000); y.r := y.r.RoundToPrecision(dpcs); y.i := y.i.RoundToPrecision(dpcs); ax.r := ax.r.RoundToPrecision(dpcs); ax.i := ax.i.RoundToPrecision(dpcs); tmp := cdiv(y, ax); ans := cmul(ans, tmp); // ans := ans * y / ax; if absz > bigdecimal.One then begin tmpy.r := pi_big / bigdecimal.two; tmpy.i := bigdecimal.Zero; ans := csub(tmpy, ans); end; result := ans; form1.Memo1.Lines.Append(' arctanR n = ' + intTostr(n)); end; // z 入力値 複素数 // eps 収束判定値 // dpcs 有効桁数 // ndis 収束表示 true 表示 false 非表示 function log_big_sub(z : Cbig; eps : bigdecimal; dpcs: integer; ndis: boolean): Cbig; const NN = 1000000; var s, x, zm1, zp1, xh2, xg, n2p1 : CBig; one, two : Cbig; xgsn : Cbig; asabs : bigdecimal; n : integer; begin one.r := Bigdecimal.One; // 1 one.r := one.r.RoundToPrecision(dpcs); one.i := Bigdecimal.Zero; // two := cadd(one, one); // 2 zm1 := csub(z, one); // z - 1 zp1 := cadd(z, one); // z + 1 x := cdiv(zm1, zp1); // x = (z-1)/(z+1) s.r := Bigdecimal.Zero; s.i := Bigdecimal.Zero; xh2 := cmul(x, x); // x^2 xg := x; // n = 0; x^(2n+1) n2p1 := one; // 2n+1 = 1 n := 0; repeat xg.r := xg.r.RoundToPrecision(dpcs); xg.i := xg.i.RoundToPrecision(dpcs); // n2p1.r := n2p1.r.RoundToPrecision(dpcs); // n2p1.i := n2p1.i.RoundToPrecision(dpcs); xgsn := cdiv(xg, n2p1); // x^(2n+1) / (2n+1) s := cadd(s, xgsn); // Σ xg := cmul(xg, xh2); // x^(2n+1) n2p1 := cadd(n2p1, two); // 2n + 1 inc(n); asabs := cabs(xgsn, dpcs); until (asabs < eps) or (n > NN); form1.Memo1.Lines.Append('ln n = ' + intTostr(n)); s := cmul(s, two); result := s; end; var z10 : cbig; Z10F : boolean = false; // z 因数 // eps 収束判定値 // dpcs 有効桁数 // 返り値 対数複素数 function log_big(z : Cbig; eps : bigdecimal; dpcs: integer): Cbig; var zb : Cbig; z10n : cbig; Zmax, ten, one, bn : bigdecimal; pi_big2: bigdecimal; begin if (z.r = 0) and (z.i = 0) then begin result.r := 0; result.i := 0; exit; end; // pi_big := pi_bigs; pi_big2 := pi_big / bigdecimal.Two; zb := z; // 虚数と実数両方ともゼロでないなら 実数部側を大きな値にして演算誤差を小さくします if (zb.r <> bigdecimal.Zero) and (zb.i <> bigdecimal.Zero) then begin if zb.i.Abs(zb.i) > zb.r.Abs(zb.r) then begin // 虚数の絶対値が実数の絶対値より大きい時入れ替え z.r := zb.i; z.i := zb.r; if zb.i < bigdecimal.Zero then begin // 虚数が負数だったら符号反転 z.r := -z.r; z.i := -z.i; end; end else begin // 虚数の絶対値が実数の絶対値と等しいか小さい時 if zb.r < bigdecimal.Zero then begin // 実数の値が負数だったら符号反転 z.r := -zb.r; z.i := -zb.i; end; end; end; // z.rが0でz.iがゼロでない時 虚数部と実数部入れ替え if (zb.r = bigdecimal.Zero) and (zb.i <> bigdecimal.Zero) then begin z.r := zb.i; z.i := zb.r; if z.r < bigdecimal.Zero then z.r := -z.r; // 実数部が負数だったら符号反転 虚数部ゼロなのでそのまま end; // 実数部が負数ので虚数部ゼロの時符号を反転 虚数部ゼロなのでそのまま if (zb.r <> bigdecimal.Zero) and (zb.i = bigdecimal.Zero) then if zb.r < bigdecimal.Zero then z.r := -zb.r; // 10の対数を利用して大きな値の計算を速くします ten := '10'; ten := ten.RoundToPrecision(dpcs); // dpcs桁合わせ one := bigdecimal.One; bn := bigdecimal.Zero; if not Z10F then begin z10.r := ten; z10.i := bigdecimal.Zero; z10 := log_big_sub(z10, eps, dpcs, false); // 10の対数 Z10F := true; end; zmax := cabs(z, dpcs); // zの絶対値 zmax := zmax.RoundToPrecision(dpcs); // dpcs桁合わせ z.r := z.r.RoundToPrecision(dpcs); // dpcs桁合わせ z.i := z.i.RoundToPrecision(dpcs); // dpcs桁合わせ // 10で除算又は乗算して値がの値が1～10の範囲に入るようにします。 repeat if zmax > ten then begin // zmaxが10より大きい時10で除算 z.r := z.r / ten; z.i := z.i / ten; zmax := zmax / ten; bn := bn + one; // 10で除算した回数 +になります。 end; if zmax < one then begin // zmaxが1より小さい時10を乗算 z.r := z.r * ten; z.i := z.i * ten; zmax := zmax * ten; bn := bn - one; // 10を乗算した回数 -になります。 end; until (zmax <= ten) and (zmax >= one); //---------------------------------------- // 修正された値で対数計算 result := log_big_sub(z, eps, dpcs, true); // 10の対数補正 z10n.r := z10.r * bn; // 加算する対数値計算10の対数値のn倍 z10n.i := z10.i * bn; result.r := result.r + z10n.r; // 10の対数値のn倍加算 result.i := result.i + z10n.i; //---------------------------------------- // z.rがゼロでz.iがゼロでない時 虚数部π/2補正 if (zb.r = bigdecimal.Zero) and (zb.i <> bigdecimal.Zero) then begin if zb.i >= bigdecimal.Zero then result.i := result.i + pi_big2 else result.i := result.i - pi_big2; end; // z.rの値が負数のきと符号を変更して計算しているの虚数部π補正。 if (zb.r < bigdecimal.Zero) and (zb.i = bigdecimal.Zero) then result.i := result.i + pi_big; // 虚数と実数両方ともゼロでない時 if (zb.r <> bigdecimal.Zero) and (zb.i <> bigdecimal.Zero) then begin // 次数部絶対値より虚数部の絶対値が大きい場合 if zb.i.Abs(zb.i) > zb.r.Abs(zb.r) then begin if zb.i > bigdecimal.Zero then result.i := -result.i + pi_big2 // π/2補正 else result.i := -result.i - pi_big2; end // 実数部が負数の時 else begin if zb.r < bigdecimal.Zero then if zb.i > bigdecimal.Zero then result.i := result.i + pi_big // π補正 else result.i := result.i - pi_big end; end; end; // ans = x^y function pow_big(x, y : cbig; eps : bigdecimal): cbig; var dpcs : integer; harf, absi, absy, four : bigdecimal; lnx, tmp : cbig; begin dpcs := BigDecimal.DefaultPrecision; if (x.r = bigdecimal.zero) and (x.i = bigdecimal.zero) then begin result.r := bigdecimal.Zero; result.i := bigdecimal.Zero; exit; end; lnx := log_big(x, eps, dpcs); // ln(x) tmp := cmul(lnx, y); // ln(x) * y result := exp_big(tmp, dpcs, eps); // xの虚数部とyの虚数部0なら if (x.i = bigdecimal.zero) and (y.i = bigdecimal.Zero) then begin harf := bigdecimal.One / bigdecimal.Two; // 0.5 absy := y.r.Abs(y.r); // yの実数部の絶対値 absi := absy.Frac; // yの実数部の絶対値の小数部 absi := absi - harf; // yの実数部の絶対値の小数部と0.5の差分 // 差分がゼロ(yの実数部の小数部が0.5) if absi = bigdecimal.Zero then // xの実数部が0と等しいか0より大きいなら if x.r >= bigdecimal.zero then result.i := bigdecimal.zero // 答えの虚数部0 // 0より小さいなら else result.r := bigdecimal.zero; // 答えの実数部0 absi := y.r.Frac; // 乗数の小数部 if absi = bigdecimal.Zero then result.i := bigdecimal.Zero; // 整数なら答えの虚数部0 end; // xの整数部とyの虚数部が0なら if (x.r = bigdecimal.Zero) and (y.i = bigdecimal.Zero) then begin absi := y.r.Frac; // 乗数の小数部 if absi = bigdecimal.Zero then begin // 整数なら absy := y.r / bigdecimal.Two; // 偶数奇数確認 absi := absy.Frac; // 小数部 if absi = bigdecimal.Zero then result.i := bigdecimal.Zero // 偶数なら虚数部0 else result.r := bigdecimal.Zero; // 奇数なら実数部0 end; end; absy := x.r.Abs(x.r); // |x.r| absi := x.i.Abs(x.i); // |x.i| // xの実数部と虚数部の絶対値が等しくてy.rがゼロでなかったら if (absy = absi) and (y.i = bigdecimal.Zero) and not (y.r = bigdecimal.Zero) then begin absi := y.r.Frac; // 乗数の小数部 if absi = bigdecimal.Zero then begin // 整数なら absy := y.r / bigdecimal.Two; // 偶数奇数確認 absi := absy.Frac; // 小数部 if absi = bigdecimal.Zero then begin // 偶数なら four := bigdecimal.Two + bigdecimal.Two; // 4 absy := y.r / four; // 4偶数奇数確認 absi := absy.Frac; // 小数部 if absi = bigdecimal.Zero then result.i := bigdecimal.Zero // 偶数なら 虚数部0 y= 4 8 else result.r := bigdecimal.Zero; // 奇数なら 虚数部0 y= 2 6 10 end; end; end; end; // 複素数の対数計算 // 50桁の精度の為 除算有効桁数100桁 procedure TForm1.Button1Click(Sender: TObject); label VA; const dpcs = 244; // 除算有効桁数 var ch : integer; zd, id, yd, yi, epsd : double; z, ans, anse, y, anssin, arctan,arctanR: cbig; eps : bigdecimal; dans, xc : variant; begin val(zedit.Text, zd, ch); if ch <> 0 then begin application.MessageBox('zの値に間違いがあります。','注意',0); exit; end; val(iedit.Text, id, ch); if ch <> 0 then begin application.MessageBox('iの値に間違いがあります。','注意',0); exit; end; val(epsedit.Text, epsd, ch); if ch <> 0 then begin application.MessageBox('収束判定値に間違いがあります。','注意',0); exit; end; if (epsd > 1e-1) then begin application.MessageBox('収束判定値は。0.01より小さくし下さい。','注意',0); exit; end; if (epsd <= 0) then begin application.MessageBox('収束判定値は。0 あるいは、負数ではいけません。','注意',0); exit; end; if checkbox2.Checked = true then begin val(yedit.Text, yd, ch); if ch <> 0 then begin application.MessageBox('yの値に間違いがあります。','注意',0); exit; end; val(yiedit.Text, yi, ch); if ch <> 0 then begin application.MessageBox('yの値に間違いがあります。','注意',0); exit; end; end; bigdecimal.DefaultPrecision := dpcs; // 入力値をテキスト形式で読み込み多倍長数値に変換します、変換誤差防止です。 z.r := zedit.Text; z.i := iedit.Text; eps := epsedit.Text; // eps := 1e-300; memo1.Clear; application.ProcessMessages; //------------------------------------------------------------------------------ memo1.Lines.Append('z= ' + z.r.ToString + ' i= ' + z.i.ToString +' i'); //---------------- power ------------------------------------------------------- if checkbox2.Checked = true then begin y.r := yedit.Text; y.i := yiedit.Text; memo1.Lines.Append('y= ' + y.r.ToString + ' i= ' + y.i.ToString +' i'); ans := pow_big(z, y, eps); ans.r := ans.r.RoundToPrecision(80); ans.i := ans.i.RoundToPrecision(80); memo1.Lines.Append('x^y = exp(ln(z)*y) = '); memo1.Lines.Append(' ' + ans.r.ToString); if ans.i >= bigdecimal.Zero then memo1.Lines.Append(' +' + ans.i.ToString + ' i') else memo1.Lines.Append(' ' + ans.i.ToString + ' i'); exit; end; //---------------------- sin --------------------------------------------------- memo1.Lines.Append('sin(z) = '); anssin := sin_big(z, eps, dpcs); anssin.r := anssin.r.RoundToPrecision(50); // 50桁に丸め anssin.i := anssin.i.RoundToPrecision(50); anssin.r := anssin.r.RemoveTrailingZeros(3); anssin.i := anssin.i.RemoveTrailingZeros(3); memo1.Lines.Append(' ' + anssin.r.ToString); if anse.i >= bigdecimal.Zero then memo1.Lines.Append(' +' + anssin.i.ToString + ' i') else memo1.Lines.Append(' ' + anssin.i.ToString + ' i'); //---------------------- arctan------------------------------------------------- memo1.Lines.Append('arctan(z) = '); if (z.r = bigdecimal.Zero) and (z.i.Abs(z.i) = bigdecimal.One) then begin memo1.Lines.Append(' ' + '0'); if z.i > bigdecimal.Zero then memo1.Lines.Append(' ' + '∞i') else memo1.Lines.Append(' ' + '-∞i'); end else begin arctan := arctan_big(z, eps, dpcs); arctan.r := arctan.r.RoundToPrecision(50); // 50桁に丸め arctan.i := arctan.i.RoundToPrecision(50); arctan.r := arctan.r.RemoveTrailingZeros(3); arctan.i := arctan.i.RemoveTrailingZeros(3); memo1.Lines.Append(' ' + arctan.r.ToString); if arctan.i >= bigdecimal.Zero then memo1.Lines.Append(' +' + arctan.i.ToString + ' i') else memo1.Lines.Append(' ' + arctan.i.ToString + ' i'); end; //---------------------- arctan Leonhard Euler ------------------------- memo1.Lines.Append('arctan_Leonhard_Euler(z) = '); if (z.r = bigdecimal.Zero) and (z.i.Abs(z.i) = bigdecimal.One) then begin memo1.Lines.Append(' ' + '0'); if z.i > bigdecimal.Zero then memo1.Lines.Append(' ' + '∞i') else memo1.Lines.Append(' ' + '-∞i'); end else begin arctanR := arctan_Leonhard_Euler(z, eps, dpcs); arctanR.r := arctanR.r.RoundToPrecision(50); // 50桁に丸め arctanR.i := arctanR.i.RoundToPrecision(50); arctanR.r := arctanR.r.RemoveTrailingZeros(3); arctanR.i := arctanR.i.RemoveTrailingZeros(3); memo1.Lines.Append(' ' + arctanR.r.ToString); if arctanR.i >= bigdecimal.Zero then memo1.Lines.Append(' +' + arctanR.i.ToString + ' i') else memo1.Lines.Append(' ' + arctanR.i.ToString + ' i'); end; //------------------------- Ln exp -------------------------------- // 虚数と実数両方ともゼロの場合-∞ if (z.r = bigdecimal.Zero) and (z.i = bigdecimal.Zero) then begin memo1.Lines.Append('loop = 0 演算出来ません。'); memo1.Lines.Append('Ln(0 + 0i) ='); memo1.Lines.Append(' -∞'); memo1.Lines.Append(' 0 i'); goto VA; end; // 対数計算 ans := log_big(z, eps ,dpcs); // exp anse := exp_big(ans, dpcs, eps); // 計算結果表示 ans.r := ans.r.RoundToPrecision(50); // 50桁に丸め ans.i := ans.i.RoundToPrecision(50); if ans.r = bigdecimal.Zero then ans.r := '0'; if ans.i = bigdecimal.Zero then ans.i := '0'; memo1.Lines.Append('Ln(z) = '); memo1.Lines.Append(' ' + ans.r.ToString); if ans.i >= bigdecimal.Zero then memo1.Lines.Append(' +' + ans.i.ToString + ' i') else memo1.Lines.Append(' ' + ans.i.ToString + ' i'); memo1.Lines.Append('exp(Ln(z)) = '); anse.r := anse.r.RoundToPrecision(50); // 50桁に丸め anse.i := anse.i.RoundToPrecision(50); anse.r := anse.r.RemoveTrailingZeros(3); anse.i := anse.i.RemoveTrailingZeros(3); memo1.Lines.Append(' ' + anse.r.ToString); if anse.i >= bigdecimal.Zero then memo1.Lines.Append(' +' + anse.i.ToString + ' i') else memo1.Lines.Append(' ' + anse.i.ToString + ' i'); // ---------------- variant Ln exp ------------------------------------------ VA: // variant double 計算 xc := varascomplex(xc); xc.real := zd; xc.Imaginary := id; if (xc.real = 0) and (xc.Imaginary = 0) then if (zd <> 0) or (id <> 0) then begin memo1.Lines.Append('variant計算'); memo1.Lines.Append(' variantの有効桁数不足で演算不可'); exit; end; if (xc.real <> 0) or (xc.Imaginary <> 0) then begin if checkbox1.Checked then begin memo1.Lines.Append('variant計算 Ln(z) = '); dans := VarComplexLn(xc); // complexLn計算 end else begin memo1.Lines.Append('variant計算 2*arctanh((z-1)/(z-1)) = '); // dans := VarComplexarctanh((xc * xc - 1)/(xc * xc + 1)); dans := lnd(zd, id); // 2arctanh{(z-1)/z+1)} 計算 end; memo1.Lines.Append(' ' + floattostr(dans.real)); if dans.Imaginary >= 0 then memo1.Lines.Append(' +' + floattostr(dans.Imaginary) + ' i') else memo1.Lines.Append(' ' + floattostr(dans.Imaginary) + ' i'); end else begin memo1.Lines.Append('variant計算 = '); memo1.Lines.Append(' -∞'); memo1.Lines.Append(' 0 i'); end; end; procedure TForm1.epsEditChange(Sender: TObject); begin Z10F := false; end; end.
log_exp_function_big.zip
三角関数、逆三角関数、その他関数 に戻る/pre