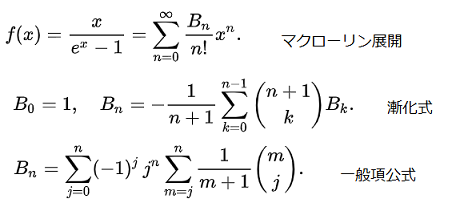ベルヌーイ数　その１

　ベルヌーイ数は、色々な関数に利用されているので、プログラムを組んでみることにしました。
ベルヌーイ数については、インターネットで検索して下さい。

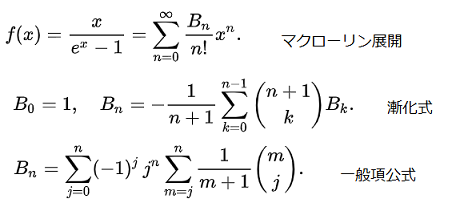　左図の計算式は、ウィキペディアに出ているものです。
基本は、マクローリン展開ですが、これでは計算が困難なので、漸化式か、一般公式でプログラムを組んでみます。

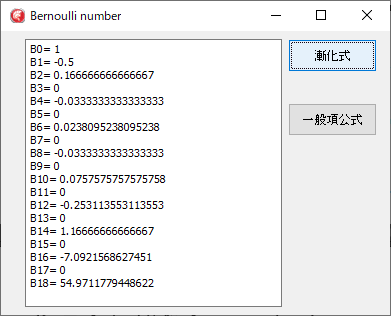　浮動小数点のExtendedで計算すると、漸化式でB18程度、一般項公式にいったってはB10程度を超えると誤差が大きくなります。

プログラム

unit main;

interface

uses
  Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
  Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.Buttons;

type
  TForm1 = class(TForm)
    BitBtn1: TBitBtn;
    Memo1: TMemo;
    BitBtn2: TBitBtn;
    procedure BitBtn1Click(Sender: TObject);
    procedure BitBtn2Click(Sender: TObject);
  private
    { Private 宣言 }
  public
    { Public 宣言 }
  end;

var
  Form1: TForm1;

implementation

{$R *.dfm}

uses system.Math;

// 階乗
function factorial(x: int64): int64;
var
  j : integer;
begin
  result := 1;
  if (x = 0) or (x = 1) then exit;
  for j := 2 to  x do
    result := result * j;
end;

// 二項係数
function binomial(n, k: integer): extended;
var
  nn, kn, knm: int64;
begin
  nn := factorial(n);
  kn := factorial(k);
  knm := factorial(n - k);
  result := nn / (kn * knm);
end;

// Bernoulli_number  計算
procedure TForm1.BitBtn1Click(Sender: TObject);
const
  N = 18;
var
  Bn: array of extended;
  i, k: integer;
  S, b, Bc: extended;
begin
  memo1.Clear;
  setlength(Bn, N + 1);
  Bn[0] := 1;
  memo1.Lines.Append('B' + intTostr(0) + '= ' + floatTostr(Bn[0]));
  for i := 1 to N do begin
    S := 0;
    for k := 0 to i -1 do begin
      b := binomial(i + 1, k);                // {(n + 1) / k}
      S := S + Bn[k] * b;                     // Σ{(n + 1) / k} Bk    k=0 to n-1
    end;
    Bn[i] := S * (-1 / (i + 1));              // Bn = -1 / (n + 1) Σ
    Bc := Bn[i];
    if i > 2 then if i mod  2 <> 0 then Bc := 0;
    memo1.Lines.Append('B' + intTostr(i) + '= ' + floatTostr(Bc));
  end;
end;

// Bernoulli_number  一般項計算
procedure TForm1.BitBtn2Click(Sender: TObject);
var
  Bn : extended;
  S  : extended;
  n, m, j: integer;
  k  : integer;
begin
  k := 10;
  memo1.Clear;
  for n := 0 to K do begin
    Bn := 0;
    for j := 0 to n do begin
      S := 0;
      for m := j to n do
        S := S + 1 / (m + 1) * binomial(m, j);
      Bn := Bn + power(-1, J) * power(j, n) * S;
    end;
    memo1.Lines.Append('B' + intTostr(n) + '= ' + floatTostr(Bn));
  end;
end;

end.