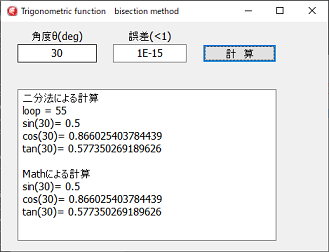
二分法による　三角関数　sin cos tan

　ゆるゆるプログラミング　三角関数　計算方法　のＪａｖａのプログラムをDelphiに変換したものです。

二分法による計算ですが、角度Degから、πを使用せずに三角関数を求めているので、参考プログラムとして取り上げてみました。
基本的に、単位は何でもよく、Rad、Grad でも求める事が出来ます。

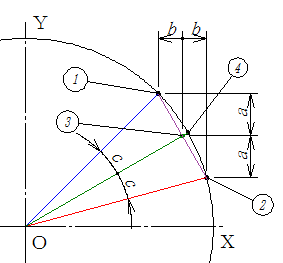　円の中心通り、円上の座標が既知の１、２を通るとすると、２つの直線の丁度中間の角度を通る直線は、１と２の座標の丁度中間の座標３をとおる直線となります。
二等辺三角形の頂角の二等分線が底辺の中点を通る事を利用しています。
円の半径を１とすれば、円上の座標４の値を容易に求めることができます。
この計算を利用して、指定角度の三角関数の近似値を求めます。
　初期値として、９０°の２つの直線として、座標を与え、目的の角度に対して、値を近づけていけば、答えの近似値を得ることが出来ます。
最初の二等辺三角形の中間点は４５°になり、次は、２２．５°か、６７．５°ですが、指定された角度が、４５°より大きければ、６７．５°となり、小さければ２２．５°となります。
順次計算していけば、指定された角度に近づけることが出来ます。
半径が１となっているので、Ｘ，Ｙの座標がそのまま、ＳｉｎとＣｏｓになります。
Ｔａｎは、Ｘの値がゼロでない限り、Ｙ／Ｘで計算されます。

　計算方法の詳細は、上記Ｌｉｎｋ先を参照してください。
ループ数は、マクローリン展開よりかなり多くなっています。
　アルゴリズムは、プログラムを読んだほうが分かりやすいと思います。

プログラム
　プログラムの中で、tan(90°)、tan(270°)の時、infinityと-infinityを返すようにしていますが、分母がゼロに対する計算、ゼロでの割り算は現在、定義されていません。

// 二分法による三角関数の計算
// https://talavax.com/math-trifunction.html にあったものをdelphiに変換しました。

unit Main;

interface

uses
  Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
  Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.Buttons, Vcl.ExtCtrls;

type
  TForm1 = class(TForm)
    LabeledEdit1: TLabeledEdit;
    BitBtn1: TBitBtn;
    Memo1: TMemo;
    LabeledEdit2: TLabeledEdit;
    procedure BitBtn1Click(Sender: TObject);
  private
    { Private 宣言 }
  public
    { Public 宣言 }
  end;

var
  Form1: TForm1;

implementation

{$R *.dfm}

uses system.Math;

function GetOrthant(deg: double): integer;
begin
  result := 0;
  if (0   < deg) and (90  > deg) then result := 1;
  if (90  < deg) and (180 > deg) then result := 2;
  if (180 < deg) and (270 > deg) then result := 3;
  if (270 < deg) and (360 > deg) then result := 4;
end;


procedure TForm1.BitBtn1Click(Sender: TObject);
var
  ch                : integer;
  orthant, loopnumber : integer;
  delta             : extended;
  deg, rad          : extended;
  deg1, deg2, degm  : extended;
  x1, y1            : extended;
  x2, y2            : extended;
  mx, my, d         : extended;
  new_x, new_y      : extended;
  ans_sin, ans_cos, ans_tan : extended;
begin
  val(LabeledEdit1.Text, deg, ch);
  if ch <> 0 then begin
    application.MessageBox('角度入力値に間違いがあります。','注意',0);
    exit;
  end;
  val(LabeledEdit2.Text, delta, ch);
  if ch <> 0 then begin
    application.MessageBox('誤差入力値に間違いがあります。','注意',0);
    exit;
  end;
  if delta >= 1 then begin
    application.MessageBox('誤差の値は１以下にして下さい。','注意',0);
    exit;
  end;
  if delta < 0 then begin
    application.MessageBox('誤差の値は０又は０以上にして下さい。','注意',0);
    exit;
  end;
  if deg < 0 then
    repeat
      deg := deg + 360;
    until deg >= 0;
  if deg >= 360 then
    repeat
      deg := deg - 360;
    until deg < 360;
  ans_sin := 0;
  ans_cos := 0;
  ans_tan := 0;
  loopnumber := 0;
  orthant := GetOrthant(deg);
  x1 := 0;
  y1 := 0;
  x2 := 0;
  y2 := 0;
  deg1 := 0;
  deg2 := 0;
  case orthant of
    1 : begin
          deg1 := 0;
          deg2 := 90;
          x1 := 1;
          y1 := 0;
          x2 := 0;
          y2 := 1;
        end;
    2:  begin
          deg1 := 90;
          deg2 := 180;
          x1 := 0;
          y1 := 1;
          x2 := -1;
          y2 := 0;
        end;
    3:  begin
          deg1 := 180;
          deg2 := 270;
          x1 := -1;
          y1 := 0;
          x2 := 0;
          y2 := -1;
        end;
    4:  begin
          deg1 := 270;
          deg2 := 360;
          x1 := 0;
          y1 := -1;
          x2 := 1;
          y2 := 0;
        end;
  end;
  if orthant = 0 then begin
    if 0 = deg then begin
      ans_sin := 0;
      ans_cos := 1;
      ans_tan := 0;
    end;
    if 90 = deg then begin
      ans_sin := 1;
      ans_cos := 0;
      ans_tan := infinity;
    end;
    if 180 = deg then begin
      ans_sin := 0;
      ans_cos := -1;
      ans_tan := 0;
    end;
    if 270 = deg then begin
      ans_sin := -1;
      ans_cos := 0;
      ans_tan := -infinity;
    end;
  end;
  if orthant > 0 then begin
    repeat
      inc(loopnumber);
      degm := (deg1 + deg2) / 2;               // 中間の角度
      mx := (x1 + x2) / 2;
      my := (y1 + y2) / 2;
      d := sqrt(mx * mx + my * my);
      new_x := mx / d;                         // 中間座標X
      new_y := my / d;                         // 中間座標y
      if deg > degm then begin               // 指定角度>中間の角度  
        x1 := new_x;                             // x1 = 中間座標X
        y1 := new_y;                             // y1 = 中間座標y
        deg1 := degm;                            // deg1 = 中間の角度
      end
      else begin                             // 指定角度<中間の角度
        x2 := new_x;                             // x2 = 中間座標X 
        y2 := new_y;                             // y2 = 中間座標y
        deg2 := degm;                            // deg2 = 中間の角度
      end;
    until abs(degm - deg) <= delta;
    ans_sin := new_y;
    ans_cos := new_x;
    ans_tan := ans_sin / ans_cos;
  end;
  memo1.Clear;
  memo1.Lines.Append('二分法による計算');
  memo1.Lines.Append('loop = ' + intTostr(loopnumber));
  memo1.Lines.Append('sin(' + floatTostr(deg) + ')= ' + floatTostr(ans_sin));
  memo1.Lines.Append('cos(' + floatTostr(deg) + ')= ' + floatTostr(ans_cos));
  memo1.Lines.Append('tan(' + floatTostr(deg) + ')= ' + floatTostr(ans_tan));
  memo1.Lines.Append('');
  memo1.Lines.Append('Mathによる計算');
  rad := deg / 180 * pi;
  memo1.Lines.Append('sin(' + floatTostr(deg) + ')= ' + floatTostr(sin(rad)));
  memo1.Lines.Append('cos(' + floatTostr(deg) + ')= ' + floatTostr(cos(rad)));
  memo1.Lines.Append('tan(' + floatTostr(deg) + ')= ' + floatTostr(tan(rad)));
end;

end.

　trigonometricA_function.zip

　　三角関数、逆三角関数、その他関数　に戻る