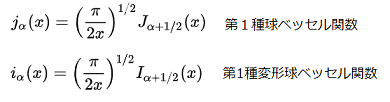第１種球ベッセル関数

ベッセル関数の詳細については、Webで検索して参照してください。

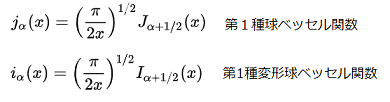　左図は第１種の球ベッセル関数の計算式ですが、第１種ベッセル関数の実数計算により簡単に求めることが出来ます。
第１種ベッセル関数の計算については、第１種ベッセル関数を参照すれば分かります。

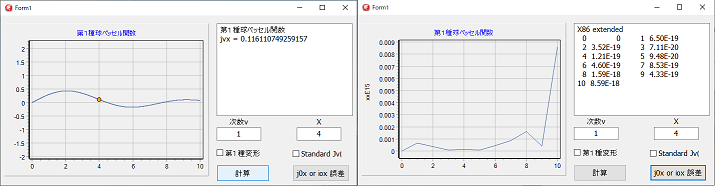
　次の図は、プログラムの実行画面です。
Xの値が大きくなると、計算の有効桁数の関係で、誤差が大きくなるのは第１種ベッセル関数と変わりません。
あまり大きな値を与えると、誤差の方が大きくなります。

プログラム

// Xの値　積分計算の上限値MNによってオーバーフローを発生するので
// コンパイル設定にオーバーフローチックが必須です。
// Xの値が大きくなると誤差が大きくなります 演算の有効桁数不足
unit Main;

interface

uses
  Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
  Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, VclTee.TeeGDIPlus,
  VCLTee.TeEngine, VCLTee.Series, Vcl.ExtCtrls, VCLTee.TeeProcs, VCLTee.Chart,
  system.UITypes;

type
  TForm1 = class(TForm)
    Button1: TButton;
    Chart1: TChart;
    Series1: TLineSeries;
    LabeledEdit2: TLabeledEdit;
    Series2: TPointSeries;
    LabeledEdit1: TLabeledEdit;
    Memo1: TMemo;
    CheckBox1: TCheckBox;
    CheckBox2: TCheckBox;
    Button2: TButton;
    procedure Button1Click(Sender: TObject);
  private
    { Private 宣言 }
    procedure Besselgraph(v, Xmax: extended; flag: boolean);
    function BesselG(X: extended; v: extended; flag: boolean): extended;
    function Log_Gamma(x: extended): extended;
    function Gamma(x: extended): extended;                 // ガンマ関数
    function Jvx(v, x: extended; flag: boolean): extended;
  public
    { Public 宣言 }
  end;

var
  Form1: TForm1;

implementation

{$R *.dfm}

uses system.math;

const

// 誤差計算用データー
  j0x: array[0..10] of extended = ( 1,
                                  0.8414709848078965066525,
                                  0.454648713412840847698,
                                  0.04704000268662240736691,
                                 -0.1892006238269820628432,
                                 -0.1917848549326276937786,
                                 -0.04656924969982097880193,
                                  0.09385522838839844148529,
                                  0.123669780827922722226,
                                  0.04579094280463961886161,
                                 -0.05440211108893698134047
                                );

  i0x: array[0..10] of extended = ( maxextended,
                                  1.175201193643801456882,
                                  1.813430203923509383834,
                                  3.339291642469967299658,
                                  6.822479299281938112227,
                                 14.8406421155577517954,
                                 33.6188595617132046875,
                                 78.33087475332093176768,
                                186.3098532236937732645,
                                450.1713224536433289461,
                               1101.323287470339337724
                                );


//ベルヌーイ数B(2)、B(4)、B(6)、...、B(20)

  B : array[1..10] of extended = ( 1.0 / 6,           // B(2)
                                  -1.0 / 30,
                                   1.0 / 42,
                                  -1.0 / 30,
                                   5.0 / 66,
                                -691.0 / 2730,
                                   7.0 / 6,
                               -3617.0 / 510,
                               43867.0 / 798,
                             -174611.0 / 330);        //  B(20)

  m: integer = sizeof(B) div sizeof(extended);

//------------------------------------------------------------------------------
// ガンマ関数
function TForm1.Log_Gamma(x: extended): extended;
var
  i : integer;
  sum : extended;
  xx, v  : extended;
  ln_sqrt_2pi: extended;
begin
  ln_sqrt_2pi := ln(sqrt(2 * pi));                    // = ln(2 * pi) / 2;
  sum := 0;
  v := 1;
  while x < m do begin
    v := v * x;
    x := x + 1;
  end;
  xx := 1 / (x * x);
  for i := m downto  2 do
    sum := (sum + B[i] / (i * 2 * (2 * i - 1))) * xx;
  result := (sum + B[1] / 2) / x
      + ln_sqrt_2pi - ln(v) - x + (x - 0.5) * ln(x);
end;

function TForm1.Gamma(x: extended): extended;  // ガンマ関数
begin
  if x < 0 then begin
    result := pi / (sin(pi * x) * exp(log_Gamma(1 - x)));
  end
  else begin
    result := exp(Log_Gamma(x));
  end;
end;

//----------------------- new --------------------------------------------------
// X 値
// v 次数
// flag false 通常 true 変形
function TForm1.Jvx(v, x: extended; flag: boolean): extended;
var
  k : integer;
  g, j, bkk, n: extended;

  function Bk(k : integer): extended;
  var
    kn : integer;
    Bn, Y, Zk: extended;
  begin
    Y := -(x / 2) * (x / 2);
    if flag then Y := -Y;
    Bn := 1;
    for kn := 1 to k do begin
      Zk := Y / (kn * (kn + v));
      Bn := Zk * Bn;
    end;
    result := Bn
  end;

begin
  n := round(v);
  if (n = v) and (n < 0) then v := abs(v);
  g := gamma(1 + v);
  bkk := 0;
  for k := 0 to 100 do bkk := bkk + Bk(k);
  j := power(x / 2, v) / g * bkk;
  if (not flag) and (abs(n) = v) and (n < 0) then j := j * Power(-1, v);
  result := j;
end;

//-----------------------------------------------------------------------------

// 第１種ベッセル関数 Γ関数使用
// X 値
// v 次数
// flag false 通常 true 変形
function TForm1.BesselG(X: extended; v: extended;  flag: boolean): extended;
const
  Mn = 50;
var
  M : Integer;
  B, S, n: extended;
begin
  n := round(v);
  if (n = v) and (n < 0) then v := abs(v);
  S := 0;
  for M := 0 to MN do begin
    B := 1 / Gamma(M + 1) / Gamma(M + v + 1);   // B = 1 / (Γ(m + 1)Γ(m + n + 1))
    if not flag then
      S := S + power(-1, M) * B * power(X / 2, 2 * M + v)
    else
      S := S + B * power(X / 2, 2 * M + v)
  end;
  if (not flag) and (abs(n) = v) and (n < 0) then S := S * Power(-1, v);
  result := S;
end;


// 第１種球ベッセル関数 グラフ表示
// v 次数
// Xmax グラフ最大値
// flag false 通常 true 変形
procedure TForm1.Besselgraph(v, Xmax: extended; flag: boolean);
const
  NMAX = 10000;
var
  Y, X: extended;
  I : integer;
  XMIN: extended;
begin
  XMIN := 0;
  x := 0;
  if v = 0 then Y := 1
           else Y := 0;
  Series1.AddXY(X, Y);
  for I := 1 to NMAX - 1 do begin
    X := XMIN + (XMAX - XMIN) * I / NMAX;
    Y := sqrt(pi/(2 * X)) * BesselG(X, v + 0.5, flag)
    Series1.AddXY(X, Y);
  end;
end;

// ベッセル球関数計算
procedure TForm1.Button1Click(Sender: TObject);
var
  ch: integer;
  X, Y, v, vs2 : extended;
  Flg: boolean;
begin
  val(LabeledEdit1.Text, v, Ch);
  if ch <> 0 then begin
    MessageDlg('次数vに間違いがあります。', mtInformation,
      [mbOk], 0, mbOk);
    exit;
  end;
  val(LabeledEdit2.Text, X, Ch);
  if ch <> 0 then begin
    MessageDlg('X値に間違いがあります。', mtInformation,
      [mbOk], 0, mbOk);
    exit;
  end;
  vs2 := 1 / 2;
  Series1.Clear;
  Series2.Clear;
  chart1.LeftAxis.AutomaticMaximum := False;
  chart1.LeftAxis.AutomaticMinimum := False;
  memo1.Clear;
  Chart1.Title.Text.Clear;
  chart1.LeftAxis.Title.Caption := '';
  if checkbox1.Checked = False then begin
    Flg := False;
    if x = 0 then begin
      if v = 0 then Y := 1
               else Y := 0;
    end
    else
      if checkbox2.Checked = false then
        Y := sqrt(pi/(2 * X)) * Jvx(v + vs2, X , Flg)
      else
        Y := sqrt(pi/(2 * X)) * BesselG(X, v + vs2, Flg);
    if Chart1.LeftAxis.Maximum <= Y + 2 then begin
      Chart1.LeftAxis.Maximum := Y + 2;
      Chart1.LeftAxis.Minimum := Y - 2;
    end
    else begin
      Chart1.LeftAxis.Minimum := Y - 2;
      Chart1.LeftAxis.Maximum := Y + 2;
    end;
    Series2.AddXY(X, Y);
    Chart1.Title.Text.Append('第１種球ベッセル関数');
    Besselgraph(v, 10, Flg);
    memo1.Lines.Add('第１種球ベッセル関数');
    memo1.Lines.Add('jvx = ' + floatTostr(Y));
  end
  else begin
    Flg := True;
    if X = 0 then begin
      if v = 0 then Y := 1
               else Y := 0;
    end
    else
      if checkbox2.Checked = false then
        Y := sqrt(pi/(2 * X)) * Jvx(v + vs2, X , Flg)
      else
        Y := sqrt(pi/(2 * X)) * BesselG(X, v + vs2, Flg);
    if Chart1.LeftAxis.Maximum <= Y + 2 then begin
      Chart1.LeftAxis.Maximum := Y + 2;
      Chart1.LeftAxis.Minimum := Y - 2;
    end
    else begin
      Chart1.LeftAxis.Minimum := Y - 2;
      Chart1.LeftAxis.Maximum := Y + 2;
    end;
    Series2.AddXY(X, Y);
    Chart1.Title.Text.Append('第１種変形球ベッセル関数');
    Besselgraph(v, 5, Flg);
    memo1.Lines.Add('第１種変形球ベッセル関数');
    memo1.Lines.Add('ivx = ' + floatTostr(Y));
  end;
end;

// 計算誤差の確認
procedure TForm1.Button2Click(Sender: TObject);
var
  flg: boolean;
  i, p, l: integer;
  jk, vs2: extended;
  def : extended;
  defs, re, ex, ads, no : string;
begin
  memo1.Clear;
  Series1.Clear;
  Series2.Clear;
  chart1.LeftAxis.AutomaticMaximum := True;
  chart1.LeftAxis.AutomaticMinimum := True;
  {$IFDEF CPUX64}
  chart1.LeftAxis.Title.Caption := 'xxE14';
  Memo1.Lines.Append('X64 extended');
  {$ELSE}
  chart1.LeftAxis.Title.Caption := 'xxE15';
  Memo1.Lines.Append('X86 extended');
  {$ENDIF}
  flg := False;
  vs2 := 1 / 2;
  if checkbox1.Checked = true then flg := true;
  for i := 0 to 10 do begin
    if i = 0 then begin
      if flg then jk := 0
             else jk := 1;
    end
    else
      if checkbox2.Checked = false then
        jk := sqrt(pi/(2 * i)) * Jvx(0 + vs2, i, flg)
      else
        jk := sqrt(pi/(2 * i)) * BesselG(i, 0 + vs2, flg);
    if flg and (i = 0) then def := 0
                       else begin
                         if flg then def := abs(i0x[i] - jk)
                                else def := abs(j0x[i] - jk);
                       end;
    {$IFDEF CPUX64}
    Series1.AddXY(i, def * 1E14);
    {$ELSE}
    Series1.AddXY(i, def * 1E15);
    {$ENDIF}
    if def <> 0 then
      defs := floatTostr(def)
    else defs := '      0';

    l := length(defs);
    p := pos('E', defs, 1);
    re := copy(defs, 0, 4);
    ex := copy(defs, p, l - p + 1);
    no := inttostr(i);
    if i < 10 then no := '  ' + no;
    if i mod 2 = 0 then
      ads := no + '  ' + re + ex
    else begin
      ads := ads + '      ' + no + '  ' + re + ex;
      memo1.Lines.Append(ads);
    end;
    if i = 10 then memo1.Lines.Append(ads);
  end;
end;

end.

　　　Spherical_Bessel1a_function.zip

各種プログラム計算例に戻る