縄跳び紐の長さ指定計算
縄跳び紐の計算は、離心率と、縄端点の支持間距離をもとに計算しますが、此処では、紐の長さから計算します。
紐の長さと、紐の端点支持距離から、離心率を求めることは、単純に出来そうにありません。
紐の長さＬと、離心率ｋは比例している様なので離心率の近似値を計算で求める事にします。
離心率が１になると、紐の長さが無限大になってしまうので、離心率の仮の値に１を与えないように注意すれば、離心率の近似値を求める事が出来ます。
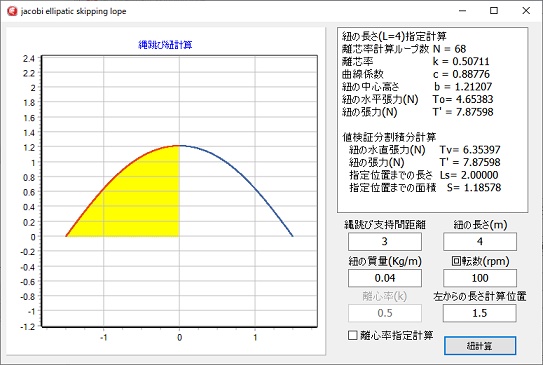左図は紐の長さ指定計算のプログラム実行例です。
離心率計算ループは６８と成っています、ニュートン法を使用していないためです。
計算判定は、判定値誤差1E-15以下としてあるので離心率の値は、精度の高い値となっています。
左端点からのXの値を与え、そこ迄の紐の長さと、その紐の形状から面積（黄色部分）を計算しています。
面積計算は、分割による積分計算です。
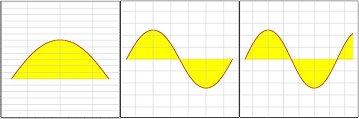左端からの長さ計算位置は、支持間距離を超えて指定することが出来ます。
ｓｎ関数はｓｉｎ関数と同じように繰り返すので、左図のような繰り返し図形となります。
プログラム
ここで使用している楕円積分は、第一二種完全楕円積分用です。
//----------------------------------------------------- // ヤコビの楕円関数と縄跳びの紐計算 // http://fuchino.ddo.jp/yatsugatake/ellipticx.pdf // http://www.wannyan.net/scidog/ellipse/ellipse.pdf //----------------------------------------------------- unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls, VclTee.TeeGDIPlus, VCLTee.TeEngine, VCLTee.Series, VCLTee.TeeProcs, VCLTee.Chart; type TForm1 = class(TForm) LabeledEdit10: TLabeledEdit; LabeledEdit11: TLabeledEdit; Memo1: TMemo; nawaBtn: TButton; Chart1: TChart; Series1: TLineSeries; Series2: TPointSeries; massEdit: TLabeledEdit; rotational_speed_Edit: TLabeledEdit; LabeledEdit1: TLabeledEdit; CheckBox1: TCheckBox; LabeledEdit2: TLabeledEdit; Series3: TLineSeries; Image1: TImage; procedure nawaBtnClick(Sender: TObject); procedure FormCreate(Sender: TObject); procedure CheckBox1Click(Sender: TObject); procedure CheckBox1KeyPress(Sender: TObject; var Key: Char); private { Private 宣言 } function jacobi_sn(u, k: double): double; procedure tension(a2, k, b, c: double); function invertK(L, a2: double): double; function Jacobi_am(u, k: double): double; procedure DrawingSet; procedure ImageClear; procedure DrawingLine(i: integer; x, y: double); procedure AreaDrawing(a2, k, b, c, Lp : double); procedure elliptic_integral(I: integer; k :double; var F, E : double); public { Public 宣言 } end; var Form1: TForm1; implementation {$R *.dfm} uses Math; var DBL_EPSILON : double; // 第一二種完全楕円積分 // 1 第一種 2 第一二種 procedure TForm1.elliptic_integral(I: integer; k :double; var F, E : double); var ch : integer; n : integer; kn : array of double; sigumaK : double; knd : array of double; kkn : array of double; Ekn : array of double; begin E := 0; if K >= 1 then begin F := Infinity; // 無限大 E := 1; exit end; n := 0; setlength(kn, 1); kn[0] := k; sigumaK := 0; while kn[n] <> sigumaK do begin // kn sigumaK := kn[n]; inc(n); setlength(kn, n + 1); kn[n] := (1 - sqrt(1 - sigumaK * sigumaK)) / (1 + sqrt(1 - sigumaK * sigumaK)); end; setlength(kn, n); // 一つ多く成っているので一つ少なく dec(n); // 一つ少なく sigumaK := 1 + kn[1]; for ch := 2 to n do begin sigumaK := sigumaK * (1 + kn[ch]); end; F := sigumaK * pi / 2; // 第一種完全楕円積分 if I = 1 then exit; setlength(knd, n); for ch := 0 to n - 1 do knd[ch] := sqrt(1- kn[ch] * kn[ch]); // kn´ setlength(kkn, n + 1); kkn[n] := pi / 2; for ch := n - 1 downto 0 do kkn[ch] := (1+ kn[ch + 1]) * kkn[ch + 1]; // kkn(kn) setlength(Ekn, n + 1); Ekn[n] := pi / 2; for ch := n - 1 downto 0 do Ekn[ch] := (1 + knd[ch]) * Ekn[ch + 1] - knd[ch] * kkn[ch]; // E(kn) E := Ekn[0]; // 第二種完全楕円積分 end; // 振幅関数 am(u, k) function TForm1.Jacobi_am(u, k: double): double; const KN = 30; var a: array of double; g: array of double; c: array of double; two_n : double; phi : double; half : double; i, j, N : integer; begin half := 1 / 2; if k = 0 then begin result := u; exit; end; if k = 1 then begin result := 2 * arctan(exp(u)) - pi / 2; exit; end; N := 1; setlength(a, KN + 1); setlength(g, KN + 1); setlength(c, KN + 1); a[0] := 1; g[0] := sqrt(1 - k * k); c[0] := k; two_n := 1; for i := 0 to KN do begin if abs(a[i] - g[i]) < a[i] * DBL_EPSILON then break; two_n := two_n + two_n; inc(N); a[i + 1] := half * (a[i] + g[i]); g[i + 1] := sqrt(a[i] * g[i]); c[i + 1] := half * (a[i] - g[i]); end; phi := two_n * a[i] * u; for j := i downto 1 do phi := half * (phi + arcsin(c[j] * sin(phi) / a[j])); result := phi; end; // ヤコビの楕円関数 function TForm1.jacobi_sn(u, k: double):double; begin result := sin(Jacobi_am(u, k)); end; // 離芯率kの計算 // L=4a/k'^2*E/K-2aのaとLが既知なのでkの値を求めます。 function TForm1.invertK(L, a2: double): double; var c, fc : double; k, E, fk : double; dk : double; N : integer; kb : double; begin a2 := abs(a2); c := (L + a2) / a2 / 2; // L=4a/k'^2*E/K-2a から判定用固定値計算 dk := 1 / 2; // Δk k := dk; // 離心率初期値 N := 0; repeat inc(N); if k >= 1 then k := 1 - DBL_EPSILON; // kが1に成った時1から僅かに小さくします。 elliptic_integral(2, k, fk, E); // 第一二種完全積分 fc := E / fk / (1 - k * k); // 判定比較値計算 if fc > c then begin // 大きかったら k := k - dk; // Δk減算 dk := dk / 2; // Δk 2分の1 end; kb = k; k := k + dk; // k+Δk until (k = kb) or (N > 200); // 収束判定 memo1.Lines.Add('離芯率計算ループ数 N = ' + intTostr(N)); result := k; end; // 紐の張力、長さ 計算 procedure TForm1.tension(a2, k, b, c: double); const KN = 1000; var ch, i : integer; p, w : double; R, T : double; Tv, T0, g : double; u, g2 : double; x, y, yb : double; dx, ty : double; snuk : double; lp, fp : double; Sl, d2 : double; Ke, E : double; begin val(massEdit.Text, p, ch); if ch <> 0 then begin application.MessageBox('紐の質量に間違いがあります。','注意', 0); exit; end; if p < 0 then begin application.MessageBox('紐の質量にマイナスはありません。','注意', 0); exit; end; val(rotational_speed_Edit.Text, R, ch); if ch <> 0 then begin application.MessageBox('回転数に間違いがあります。','注意', 0); exit; end; w := R / 60 * pi * 2; // 角速度 ω g := p * w * w; // γ=ρ*ω^2 elliptic_integral(1, k, ke, E); // 第一種完全積分 T0 := g * a2 * a2 / 4 / (1 - k * k) / Ke / Ke; memo1.Lines.Add('紐の水平張力(N) To= ' + floatTostrF(T0, ffFixed, 10, 5)); T := T0 * sqrt(b * b / c / c + 1); memo1.Lines.Add('紐の張力(N) T'' = ' + floatTostrF(T, ffFixed, 10, 5)); memo1.Lines.Add(''); memo1.Lines.Add('値検証分割積分計算'); g2 := g / 2; // 平均向心力計算の為二分の一にします dx := a2 / KN / 2; // Δx d2 := dx * dx; Tv := 0; Sl := 0; yb := 0; for i := 1 to KN do begin // 中央迄積分 x := i * dx; // x位置 u := x / c; // F(α,k)=u snuk := jacobi_sn(u, k); // jacobi_sn ヤコビの楕円関数 y := snuk * b; // x位置のyの値 ty := (y - yb); // Δy lp := sqrt(d2 + ty * ty); // Δl Sl := Sl + lp; // L合計 fp := lp * (y + yb) * g2; // yとybの平均向心力 Tv := Tv + fp; // F合計 yb := y; end; // 紐の長さ Sl := Sl * 2; if checkbox1.Checked then memo1.Lines.Add(' 紐の 長さ L'' = ' + floatTostrF(Sl, ffFixed, 10, 5)); memo1.Lines.Add(' 紐の水直張力(N) Tv= ' + floatTostrF(Tv, ffFixed, 10, 5)); if b = 0 then T := 0 else T := Tv * sqrt(c * c / b / b + 1); // T := Tv / b * sqrt(b * b + c * c); memo1.Lines.Add(' 紐の張力(N) T'' = ' + floatTostrF(T, ffFixed, 10, 5)); end; var xbase, ybase : integer; // 基準座標値 xsb, ysb : double; // グラフ基準値 xs, ys : double; // 座標変換係数値 // 線の描画 // 0 : Move 1 : Lineto procedure TForm1.DrawingLine(i: integer; x, y: double); var xpos, ypos: integer; begin // (X値 - X基準値) * X座標変換係数 + X基準座標 xpos := round((x - xsb) * xs) + xbase; // (Y値 - Y基準値) * Y座標変換係数 + Y基準座標 ypos := round((y - ysb) * ys) + ybase; if i = 0 then Image1.Canvas.MoveTo(xpos, ypos) else Image1.Canvas.LineTo(xpos, ypos); end; // 背景図描画設定 procedure TForm1.DrawingSet; begin with series2 do begin xbase := calcXpos(1); // 左端のX座標 X基準座標 ybase := calcYpos(1); // 下端のY座標 Y基準座標 xsb := XValues.Items[2] - XValues.Items[1]; // X軸範囲 xs := (calcXpos(2) - calcXpos(1)) / xsb; // X座標への変換係数 xsb := XValues.Items[1]; // 左端の値 X基準値 ysb := YValues.Items[0] - YValues.Items[1]; // y軸範囲 ys := (calcYpos(0) - calcYpos(1)) / ysb; // Y座標への変換係数 ysb := YValues.Items[1]; // 下端の値 Y基準値 end; end; // 計算指定範囲塗りつぶし procedure TForm1.AreaDrawing(a2, k, b, c, Lp : double); var i : integer; dx, x, y, u, snuk: double; a : double; begin DrawingSet; // グラフ作図 a := a2 / 2; dx := 3 / xs; // ピッチ設定 Image1.Canvas.Pen.Width := 3; // 線の幅 塗りつぶしになる線幅 Image1.Canvas.Pen.Color := clYellow; // 塗りつぶし色 i := 0; x := 0; repeat u := x / c; // F(α,k)=u snuk := jacobi_sn(u, k); // jacobi_sn ヤコビの楕円関数 y := snuk * b; // x位置のyの値 DrawingLine(0, x - a, y); // moveTo(x,y) DrawingLine(1, x - a, 0); // lineTo(x,y) inc(i); x := i * dx; // x位置 until x >= Lp; // 指定位置迄 Chart1.BackImage.Bitmap := Image1.Picture.Bitmap; // グラフ背景にImage1コピー end; // 縄跳びの縄弛み計算 procedure TForm1.nawaBtnClick(Sender: TObject); var KN : integer; k : double; ch : integer; a, a2 : double; fkd, b, u : double; c, L : double; i : integer; x, y, dx : double; snuk : double; ty, by : double; lx, rx : double; def, ddf : double; Ek : double; Lk : double; siguma : double; Lp, LLP : double; dx2 : double; S : double; Lb : double; begin KN := 1000; k := 0; // 離心率 L := 0; // 紐長さ val(Labelededit10.Text, a2, ch); if ch <> 0 then begin application.MessageBox('縄跳び紐支持間に間違いがあります。','注意',0); exit; end; if a2 < 0 then begin application.MessageBox('支持間の値にマイナスはありません。','注意',0); exit; end; val(Labelededit2.Text, Lp, ch); if ch <> 0 then begin application.MessageBox('左からの位置に間違いがあります。','注意',0); exit; end; if Lp < 0 then begin application.MessageBox('左からの位置にマイナスはありません。','注意',0); exit; end; if checkbox1.Checked then begin val(LabeledEdit1.Text, k, ch); if ch <> 0 then begin application.MessageBox('縄跳び紐離心率Ｋに間違いがあります。','注意',0); exit; end; if k >= 1 then begin application.MessageBox('k(離心率)の値を１以下にして下さい。','注意',0); exit; end; if k < 0 then begin application.MessageBox('k(離心率)の値にマイナスはありません。','注意',0); exit; end; end else begin val(LabeledEdit11.Text, L, ch); if ch <> 0 then begin application.MessageBox('縄跳び紐の長さに間違いがあります。','注意',0); exit; end; if L <= abs(a2) then begin application.MessageBox('紐の長さは支持間より長くしてください。','注意',0); exit; end; end; memo1.Clear; if not checkbox1.Checked then begin memo1.Lines.Add('紐の長さ(L=' + floatTostr(L) + ')指定計算'); k := invertK(L, a2); // 離芯率kの計算 memo1.Lines.Add('離芯率 k = ' + floatTostrF(k, ffFixed, 10, 5)); end else memo1.Lines.Add('離心率(k=' + floatTostr(k) + ')指定計算'); elliptic_integral(2, k, fkd, Ek); // 第一二種完全積分 if abs(k) = 0 then begin application.MessageBox('離心率がゼロです。','注意',0); exit; end; // 各種計算 a := a2 / 2; c := a / fkd; // 積分値に対する曲線係数 b := 2 * k / (1 - k * k) * c; // 最大値 中央の位置 memo1.Lines.Add('曲線係数 c = ' + floatTostrF(c, ffFixed, 10, 5)); memo1.Lines.Add('紐の中心高さ b = ' + floatTostrF(b, ffFixed, 10, 5)); // 紐の長さ計算 中間位置の計算は出来ません if checkbox1.Checked then begin Lk := 4 * c * Ek / (1 - k * k) - a2; // 弧の長さ計算 memo1.Lines.Add('紐の長さ L = ' + floatTostrF(Lk, ffFixed, 10, 5)); end; Series1.Clear; Series2.Clear; Series3.Clear; ImageClear; application.ProcessMessages; // グラフスケール設定 Lb := 0; // Lb 縄高さ最小値 if (Lp > a2) then if (Lp < a2 * 1.5) then begin x := Lp; // x位置 u := x / c; // F(α,k)=u snuk := jacobi_sn(u, k); // jacobi_sn ヤコビの楕円関数 Lb := snuk * b; // 縄の支持間より計算指定位置が大きい場合 end else Lb := -b; // 縄の支持間より計算指定位置が1.5倍以上ある場合 // 半周期pi/2の範囲のみ等倍表示設定 if (a2 > abs(b)) or (Lp > abs(b)) then begin ddf := a2 / 10; // 余白 def := (a2 - b) / 2; // 上下追加余白 ty := b + def + ddf; by := Lb - def - ddf; rx := a + ddf; if Lp > a2 then // 右端計算指定位置が支持位置より右側だったら rx := Lp - a + ddf; // 右端を右端計算位置に設定 lx := -a - ddf; end else begin ddf := b / 10; // 余白 def := (b - a2) / 2; // 左右追加余白 ty := b + ddf; by := 0 - ddf; rx := a + def + ddf; lx := -a - def - ddf; if a2 < Lp then begin // 右端計算指定位置が支持位置より右側だったら rx := Lp + ddf - a; // 右端を右端計算位置に設定 lx := -a - ddf; // 左端余白変更 end; end; // グラフのスケール設定値セット // Series2はグラフ上不可視設定 Series2.AddXY(lx, ty); Series2.AddXY(lx, by); Series2.AddXY(rx, by); application.ProcessMessages; // グラフ表示待ち // グラフ作図 dx := a2 / KN; // ΔX // 0～KN 計算作図 for i := 0 to KN do begin x := i * dx; // x位置 u := x / c; // F(α,k)=u snuk := jacobi_sn(u, k); // jacobi_sn ヤコビの楕円関数 y := snuk * b; // x位置のyの値 Series1.AddXY(x - a, y); // グラフに追加 end; application.ProcessMessages; // グラフ表示待ち // 端点張力計算 tension(a2, k, b, c); // 長さ分割積分 KN := round(Lp / a2 * 100); if KN = 0 then KN := 1; KN := KN * 10; dx := Lp / KN; // ΔX dx2 := dx / 2; // ΔX / 2 siguma := 0; // 長さ用合計値クリア S := 0; // 面積用合計値クリア // 長さ積分範囲スタート位置 Series3.AddXY(0 - a, 0); // グラフに追加 // 指定範囲長さ面積分割積分計算 for i := 0 to KN - 1 do begin x := i * dx + dx2; // +dx2 は x位置中間位置で計算の為 u := x / c; // F(α,k)=u // jacobi_sn ヤコビの楕円関数 αの計算 snuk := jacobi_sn(u, k); // jacobi_sn(u, k) y := snuk * b; Series3.AddXY(x - a, y); // グラフに追加 S := S + abs(y); // 面積用 ∑y y := (1 - k * k * snuk * snuk); // dn^2(u) = 1-K^2*sn^2(u) siguma := siguma + y; // 長さ計算用積分 合計値 end; // 長さ積分範囲表示の為の追加です長さ計算には関係ありません u := Lp / c; // F(α,k)=u snuk := jacobi_sn(u, k); // jacobi_sn(u, k) y := snuk * b; Series3.AddXY(Lp - a, y); // グラフに追加 application.ProcessMessages; // グラフ表示待ち //-------------------------------------------------------- LLP := 2 / (1- k * k) * siguma * dx - Lp; // 長さ memo1.Lines.Add(' 指定位置までの長さ Ls= ' + floatTostrF(LLP, ffFixed, 10, 5)); S := S * dx; // 面積計算 ∑y * dx memo1.Lines.Add(' 指定位置までの面積 S= ' + floatTostrF(S, ffFixed, 10, 5)); AreaDrawing(a2, k, b, c, Lp); end; // 紐の長さ(L)指定と離心率(K)計算の指定切り替え procedure TForm1.CheckBox1Click(Sender: TObject); begin if CheckBox1.Checked then begin labeledEdit1.Enabled := True; labeledEdit11.Enabled := False; end else begin labeledEdit1.Enabled := False; labeledEdit11.Enabled := True; end; end; // タブオーダーによるCheckBox選択時キー入力割り込みでチェックセット procedure TForm1.CheckBox1KeyPress(Sender: TObject; var Key: Char); begin if CheckBox1.Checked then CheckBox1.Checked := False else CheckBox1.Checked := True; end; // グラフ背景消去 procedure TForm1.ImageClear; begin Image1.Canvas.Brush.Style := bsSolid; Image1.Canvas.Brush.Color := clWhite; Image1.Canvas.FillRect(rect(0, 0, Image1.Width, Image1.Height)); Image1.Canvas.Brush.Style := bsClear; Chart1.BackImage.Bitmap := Image1.Picture.Bitmap; // グラフ背景にImage1コピー end; // 起動時設定 // グラフ背景用ビットマップ設定 procedure TForm1.FormCreate(Sender: TObject); var bm : Tbitmap; x, y, z : double; i : integer; begin i := 0; x := 1; y := 1; repeat y := y / 2; z := x + y; inc(i); until (z = x) or (i > 100); labeledEdit1.Enabled := False; // Edit1入力禁止 bm := Tbitmap.Create; // bitmap生成 bm.Width := Chart1.Width; bm.Height := Chart1.Height; Image1.Width := Chart1.Width; Image1.Height := Chart1.Height; Image1.Picture.Bitmap := bm; // Image1にビットマップ割り付け Image1.Visible := False; // Image1非表示 bm.Free; // bitmap開放 ImageClear; // Image1消去 end; end.
jacobi_skipping_rope_fixed_Landen.zip