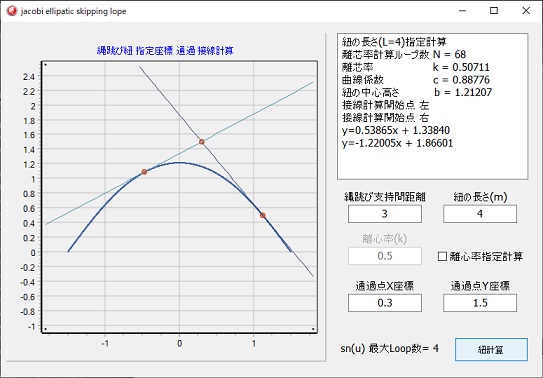
 通過点を指定した、接線は、左図の様に接線が二本になる場合と、一本になる場合、さらに無い場合があります。
通過点を指定した、接線は、左図の様に接線が二本になる場合と、一本になる場合、さらに無い場合があります。通過点は、X座標と、Y座標の値を指定します。
縄跳び紐との接線その3
此処では、通過点を指定した接線の値を求めます。
 通過点を指定した、接線は、左図の様に接線が二本になる場合と、一本になる場合、さらに無い場合があります。
通過点を指定した、接線は、左図の様に接線が二本になる場合と、一本になる場合、さらに無い場合があります。
通過点は、X座標と、Y座標の値を指定します。
指定点を通る接線がある場合の条件
A.指定点のY座標が0より大きい時
1.指定点のX座標が、縄のX範囲内にある場合は、縄の曲線より上にある事
2.縄の左端点と、指定点間の傾きが、縄の左端点の傾きより小さい事
3.縄の右端点と、指定点間の傾きが、縄の右端点の傾きより小さい事
1,2を満足する場合は左一本 1,3を満足する場合は右一本 1,2,3を満足する場合は、二本
*傾きの大小の範囲は、回転方法で判断します。
B.指定点のY座標が0より小さい時 2.縄の左端点と、指定点間の傾きが、縄の左端点の傾きより小さい事
1.指定点のX座標が、縄のX範囲外にある事
2.縄の左端点と、指定点間の傾きが、縄の左端点の傾きより小さい事
3.縄の右端点と、指定点間の傾きが、縄の右端点の傾きより小さい事
接線の数は一本
接点の計算
接点の計算で、連立方程式をたてることは可能ですが、楕円積分関数が入る為、解くことが難しいので、前記条件で、紐曲線の端点から、傾きを計算、指定点との傾きが一致する点を検索します。
通過指定点と、縄跳び紐の端点が一致する場合は、単に紐曲線端点の傾斜とします。
計算の収束計算に DBL_EPSILON を使用しています。
DBL_EPSILONは、Cの場合 1 + xE-y = 1 となる時の寸前値で、規格は 1E-9 以下となっています。
実際の計算では、もっと小さな値で C の場合Doubleで 2.22044604925031E-16 、Delphiには DBL_EPSILON の値は設定されていません。
DBL_EPSILONの設定手順です。
x = 1 /
2から始めて x = x / 2 を繰り返し
1 + x = 1
になってしまう x の値を求め、 1 + x > 1 となる最小値として DBL_EPSILON = x * 2
とします。
この場合乗算が速いからと、0.5の使用は避けるようにします、0.5と1/2には僅かな誤差が生じます。
各精度での値は
Double DBL_EPSILON = 2.22044604925031E-16
Extended LDBL_EPSILON = 1.08420217248550443E-19
Single
FLT_EPSILON = 1.1920929E-7
プログラム
//----------------------------------------------------- // ヤコビの楕円関数と縄跳びの紐計算 // http://fuchino.ddo.jp/yatsugatake/ellipticx.pdf // http://www.wannyan.net/scidog/ellipse/ellipse.pdf //----------------------------------------------------- unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls, VclTee.TeeGDIPlus, VCLTee.TeEngine, VCLTee.Series, VCLTee.TeeProcs, VCLTee.Chart; type TForm1 = class(TForm) LabeledEdit10: TLabeledEdit; LabeledEdit11: TLabeledEdit; Memo1: TMemo; nawaBtn: TButton; Chart1: TChart; Series1: TLineSeries; Series2: TPointSeries; Xpoint_Edit: TLabeledEdit; Ypoint_Edit: TLabeledEdit; LabeledEdit1: TLabeledEdit; CheckBox1: TCheckBox; Label1: TLabel; Series3: TPointSeries; Series4: TLineSeries; Series5: TLineSeries; procedure nawaBtnClick(Sender: TObject); procedure FormCreate(Sender: TObject); procedure CheckBox1Click(Sender: TObject); procedure CheckBox1KeyPress(Sender: TObject; var Key: Char); private { Private 宣言 } function jacobi_sn(u, k: double): double; function invertK(L, a2: double): double; procedure tangent(a, b, c, k, xp, yp: double); procedure Linedraw(a0, a1, c0, c1: double; RF, LF: boolean); procedure Complete_Elliptic_Integrals(k: double; var Fk, Ek: double); public { Public 宣言 } end; var Form1: TForm1; implementation {$R *.dfm} uses Math; var Ns : integer; DBL_EPSILON : double; // 第一二種完全楕円積分 // K 離心率 // Fk 第一種 // Ek 第二種 procedure TForm1.Complete_Elliptic_Integrals(k: double; var Fk, Ek: double); const KN = 30; var m : double; // the parameter of the elliptic function m = k^2 a : double; // arithmetic mean g : double; // geometric mean a_old : double; // previous arithmetic mean g_old : double; // previous geometric mean two_n : integer; // power of 2 sum : double; half : double; N : integer; // loop数 begin half := 1 / 2; if k = 0 then begin Fk := PI / 2; Ek := Fk; exit; end; m := k * k; if m = 1 then begin Fk := infinity; Ek := 1; exit; end; a := 1; g := sqrt(1 - m); two_n := 1; sum := (2 - m); N := 0; while N < KN do begin // 収束しなかった時KN回で終了 g_old := g; a_old := a; a := (g_old + a_old) * half; g := sqrt(g_old * a_old); two_n := two_n + two_n; sum := sum - two_n * (a * a - g * g); if abs(a_old - g_old) <= a_old * DBL_EPSILON then break; inc(N); end; Fk := PI / 2 / a; Ek := PI / 4 / a * sum; end; // Jacobi関数 Jacobi sn(u, k) function TForm1.Jacobi_sn(u, k: double): double; const KN = 30; var a: array of double; g: array of double; c: array of double; two_n : integer; phi : double; half : double; i, j, N : integer; begin half := 1 / 2; if k = 0 then begin result := sin(u); exit; end; if k = 1 then begin result := sin(2 * arctan(exp(u)) - pi / 2); exit; end; N := 1; setlength(a, N); setlength(g, N); setlength(c, N); a[0] := 1; g[0] := sqrt(1 - k * k); c[0] := k; two_n := 1; for i := 0 to KN do begin // 収束しなかった時KNで終了 if abs(a[i] - g[i]) < a[i] * DBL_EPSILON then break; two_n := two_n + two_n; inc(N); setlength(a, N); setlength(g, N); setlength(c, N); a[i + 1] := half * (a[i] + g[i]); g[i + 1] := sqrt(a[i] * g[i]); c[i + 1] := half * (a[i] - g[i]); end; Ns := i; phi := two_n * a[i] * u; for j := i downto 1 do phi := half * (phi + arcsin(c[j] * sin(phi) / a[j])); result := sin(phi); end; // 離芯率kの計算 // L=4a/k'^2*E/K-2aのaとLが既知なのでkの値を求めます。 function TForm1.invertK(L, a2: double): double; const KN = 500; var c, fc : double; k, E, Fk : double; dk : double; N : integer; begin a2 := abs(a2); c := (L + a2) / a2 / 2; // L=4a/k'^2*E/K-2a から判定用固定値計算 k := 0; // 離心率初期値 dk := 1 / 2; // Δk N := 0; repeat inc(N); k := k + dk; // k+Δk if k >= 1 then k := 1 - DBL_EPSILON; // kが1に成った時1から僅かに小さくします。 Complete_Elliptic_Integrals(k, Fk, E); fc := E / Fk / (1 - k * k); // 判定比較値計算 if fc > c then begin // 大きかったら k := k - dk; // Δk減算 dk := dk / 2; // Δk 2分の1 end; until (dk < DBL_EPSILON * k) or (N > KN); // 収束判定 memo1.Lines.Add('離芯率計算ループ数 N = ' + intTostr(N)); result := k; end; // 接線の描画 // a0, a1 接線の傾斜 // c0, c1 接線の切片 procedure TForm1.Linedraw(a0, a1, c0, c1: double; RF, LF: boolean); const KN = 100; var t, b, l, r: double; w : double; x, dx, y : double; i : integer; begin if not RF and not LF then exit; t := Series2.YValue[0]; // グラフ上限 b := Series2.YValue[1]; // グラフ下限 l := Series2.XValue[1]; // グラフ左限 r := Series2.XValue[2]; // グラフ右限 w := r - l; // 幅 dx := w / KN; // 描画間隔 for i := 0 to KN do begin x := i * dx + l; if LF then begin y := a0 * x + c0; if (y < t) and (y > b) then Series4.AddXY(x, y); end; if RF then begin y := a1 * x + c1; if (y < t) and (y > b) then Series5.AddXY(x, y); end; end; end; // 接線の計算 // a 縄跳びの間隔の二分の一 90°分 // b 紐の高さ // c 紐の係数 (端点の傾斜b/c) // xp, yp 通過点の座標 procedure TForm1.tangent(a, b, c, k, xp, yp: double); const KN = 100; var alpha : double; // 端点傾斜角 La, Ra : double; // 傾斜 LF, RF : boolean; // 接線有無フラグ yc, u : double; snuk : double; sn2uk : double; x, y, dx : double; N : integer; Salpha : double; // 直線の傾斜 a0, a1 : double; // 接線の傾斜 c0, c1 : double; // 接線の切片 begin // 接点があるか確認 alpha := b / c; yc := 0; if (xp > -a) and (a > xp) then begin // xpの座標が縄間隔内なら yc計算 u := (xp + a) / c; // F(α,k)=u u ゼロ基準に(x + a) snuk := jacobi_sn(u, k); // jacobi_sn ヤコビの楕円関数 yc := snuk * b; // x位置のyの値 end; La := MaxDouble; // 最大値セット∞の代わり Ra := -La; // 最小値セット-∞の代わり LF := False; RF := False; if yp >= yc then begin // ycよりypが大きい場合 if xp <> -a then La := yp / (xp + a); // 左端点の傾斜計算 if xp <> a then Ra := yp / (xp - a); // 右端点の傾斜計算 if (La < alpha) and (Xp > -a) then LF := True; // 左の傾斜が端点の傾斜より小さい場合True if (Ra > -alpha) and (Xp < a) then RF := True; // 右の傾斜が端点の傾斜より小さい場合True end; if (yp < 0) then begin // ypがゼロより小さい場合 if xp < -a then La := yp / (xp + a); // 左端点の傾斜計算 if xp > a then Ra := yp / (xp - a); // 右端点の傾斜計算 if (La < alpha) and (Xp < -a) then RF := True; // 左端点の傾斜が小さい場合右True if (Ra > -alpha) and (Xp > a) then LF := True; // 右端点の傾斜が小さい場合左True end; // 接点があったら接点位置の計算 dx := a * 2 / KN; // Δx=a2/KN N := 0; x := 0; a0 := 0; if LF then begin // 左端から接線位置検索 repeat x := x + dx; // x位置 u := x / c; // F(α,k)=u snuk := jacobi_sn(u, k); // jacobi_sn ヤコビの楕円関数 y := snuk * b; // x位置のyの値 sn2uk := snuk * snuk; alpha := b / c * sqrt((1 - sn2uk) * (1 - k * K * sn2uk)); // 紐曲線の傾き Salpha := (yp - y) / (xp - (x - a )); // 直線の傾き if x > a then alpha := -alpha; // 微分値がプラスのみなのでXの値で-設定 if Salpha > alpha then begin // 直線の傾斜が曲線の傾斜より大きくなったら x := x - dx; // xの値戻し dx := dx / 2; // dx二分の一 N := 0; // 加算回数クリア end else inc(N); until (N > KN) or (dx < DBL_EPSILON * x); Series3.AddXY(x - a, y); // 通過指定点 a0 := Salpha; // 接線1の傾斜 end; dx := a * 2 / KN; // Δx=a2/KN N := 0; x := 0; a1 := 0; if RF then begin // 右端から接線位置検索 repeat x := x + dx; // x位置 u := (a + a - x) / c; // F(α,k)=u snuk := jacobi_sn(u, k); // jacobi_sn ヤコビの楕円関数 y := snuk * b; // x位置のyの値 sn2uk := snuk * snuk; alpha := b / c * sqrt((1 - sn2uk) * (1 - k * K * sn2uk)); // 紐曲線の傾き Salpha := (yp - y) / (xp - (a - x)); // 直線の傾き if (a + a - x) > a then alpha := -alpha; // 微分値がプラスのみなのでXの値で-設定 if Salpha < alpha then begin // 直線の傾斜が曲線の傾斜より小さくなったら x := x - dx; // xの値戻し dx := dx / 2; // dx二分の一 N := 0; // 加算回数クリア end else inc(N); // 加算回数 until (N > KN) or (dx < DBL_EPSILON * x); // 加算回数が上限を超える又はdxが指定値より小さくなったら Series3.AddXY((a - x), y); // 通過指定点 a1 := Salpha; // 接線2の傾斜 end; c0 := 0; if (abs(xp) = a) and (yp = 0) then begin // 指定点が縄端点なら if xp < 0 then begin a0 := alpha; LF := True; end else begin a1 := -alpha; RF := True; end; end; if LF then memo1.Lines.Add('接線計算開始点 左'); if RF then memo1.Lines.Add('接線計算開始点 右'); if not LF and not RF then memo1.Lines.Add('接線無し'); if LF then begin c0 := yp - a0 * xp; // 切片の計算 memo1.Lines.Add('y=' + floatTostrF(a0,fffixed, 10,5) + 'x + ' + floatTostrF(c0,fffixed, 10,5)); end; c1 := 0; if RF then begin c1 := yp - a1 * xp; // 切片の計算 memo1.Lines.Add('y=' + floatTostrF(a1,fffixed, 10,5) + 'x + ' + floatTostrF(c1,fffixed, 10,5)); end; Linedraw(a0, a1, c0, c1, RF, LF); // 接線の描画 end; // 縄跳びの縄弛み計算 procedure TForm1.nawaBtnClick(Sender: TObject); const kN = 400; var k : double; ch : integer; a, a2 : double; b, u : double; c, L : double; i : integer; x, y, dx : double; snuk : double; ty, by : double; lx, rx : double; def, ddf : double; Ek, Fk : double; Lk : double; xp, yp : double; xmax, xmin : double; ymax, ymin : double; begin Ns := 0; // sn(u,k)ループ数 k := 0; // 離心率 L := 0; // 紐長さ val(Labelededit10.Text, a2, ch); if ch <> 0 then begin application.MessageBox('縄跳び紐支持間に間違いがあります。','注意',0); exit; end; if a2 <= 0 then begin application.MessageBox('縄跳び紐支持間はゼロ以上にして下さい。','注意',0); exit; end; val(Xpoint_Edit.Text, xp, ch); if ch <> 0 then begin application.MessageBox('X座標の値に間違いがあります。','注意',0); exit; end; val(Ypoint_Edit.Text, yp, ch); if ch <> 0 then begin application.MessageBox('Y座標の値に間違いがあります。','注意',0); exit; end; if checkbox1.Checked then begin val(LabeledEdit1.Text, k, ch); if ch <> 0 then begin application.MessageBox('縄跳び紐離心率Kに間違いがあります。','注意',0); exit; end; if k > 1 then begin application.MessageBox('k(離心率)の最大値は1です。','注意',0); exit; end; if k < 0 then begin application.MessageBox('k(離心率)の値にマイナスはありません。','注意',0); exit; end; end else begin val(LabeledEdit11.Text, L, ch); if ch <> 0 then begin application.MessageBox('縄跳び紐の長さに間違いがあります。','注意',0); exit; end; if L <= abs(a2) then begin application.MessageBox('紐の長さは支持間より長くしてください。','注意',0); exit; end; end; memo1.Clear; if not checkbox1.Checked then begin memo1.Lines.Add('紐の長さ(L=' + floatTostr(L) + ')指定計算'); k := invertK(L, a2); // 離芯率kの計算 memo1.Lines.Add('離芯率 k = ' + floatTostrF(k, ffFixed, 10, 5)); end else memo1.Lines.Add('離心率(k=' + floatTostr(k) + ')指定計算'); Complete_Elliptic_Integrals(k, Fk, Ek); // 第一二種完全積分 if abs(k) = 1 then begin application.MessageBox('離心率の絶対値が1です1以下にして下さい。','注意',0); exit; end; if abs(k) = 0 then begin application.MessageBox('離心率がゼロです。','注意',0); exit; end; // 各種計算 a := a2 / 2; c := a / Fk; // 積分値に対する曲線係数 b := 2 * k / (1 - k * k) * c; // 最大値 中央の位置 memo1.Lines.Add('曲線係数 c = ' + floatTostrF(c, ffFixed, 10, 5)); memo1.Lines.Add('紐の中心高さ b = ' + floatTostrF(b, ffFixed, 10, 5)); // 紐の長さ計算 中間位置の計算は出来ません if checkbox1.Checked then begin Complete_Elliptic_Integrals(k, Fk, Ek); // 第一二種完全積分 Lk := 4 * c * Ek / (1 - k * k) - a2; // 弧の長さ計算 memo1.Lines.Add('紐の長さ L = ' + floatTostrF(Lk, ffFixed, 10, 5)); end; Series1.Clear; Series2.Clear; Series3.Clear; Series4.Clear; Series5.Clear; xmax := a; xmin := -a; ymax := b; ymin := 0; if xmax < xp then xmax := xp; if xmin > xp then xmin := xp; if ymax < yp then ymax := yp; if ymin > yp then ymin := yp; // グラフスケール設定 if (xmax - xmin) > (ymax - ymin) then begin ddf := (xmax - xmin) / 10; def := ((xmax - xmin) - (ymax - ymin)) / 2; ty := ymax + def + ddf; by := ymin - def - ddf; rx := xmax + ddf; lx := xmin - ddf; end else begin ddf := (ymax - ymin) / 10; def := ((ymax - ymin) - (xmax - xmin)) / 2; ty := ymax + ddf; by := ymin - ddf; rx := xmax + def + ddf; lx := xmin - def - ddf; end; // グラフのスケール設定値セット Series2.AddXY(lx, ty); Series2.AddXY(lx, by); Series2.AddXY(rx, by); application.ProcessMessages; // グラフ表示待ち // グラフ作図 dx := a / KN; // ΔX // 0~KN 計算作図 for i := -KN to KN do begin x := i * dx; // x位置 u := (x + a) / c; // F(α,k)=u u ゼロ基準に(x + a) snuk := jacobi_sn(u, k); // jacobi_sn ヤコビの楕円関数 y := snuk * b; // x位置のyの値 Series1.AddXY(x, y); // グラフに追加 end; Series3.AddXY(xp, yp); // 通過指定点 application.ProcessMessages; // グラフ表示待ち tangent(a, b, c, k, xp, yp); // 接線の計算 Label1.Caption:= 'sn(u) 最大Loop数= ' + intTostr(Ns); end; procedure TForm1.CheckBox1Click(Sender: TObject); begin if CheckBox1.Checked then begin labeledEdit1.Enabled := True; labeledEdit11.Enabled := False; end else begin labeledEdit1.Enabled := False; labeledEdit11.Enabled := True; end; end; procedure TForm1.CheckBox1KeyPress(Sender: TObject; var Key: Char); begin if CheckBox1.Checked then CheckBox1.Checked := False else CheckBox1.Checked := True; end; // 初期設定 // DBL_EPSILON 桁落ち値の設定 1 + y = 1 のyの値検出 y = 1E-i // DBL_EPSILON = y * 10; procedure TForm1.FormCreate(Sender: TObject); const IM = 50; var x, y, z : double; i : integer; begin labeledEdit1.Enabled := False; x := 1; y := 1 / 4194304; // 4194304 = 2^22 repeat y := y / 2; z := x + y; until (z = 1) or (i > IM); DBL_EPSILON := y * 2; end; end.
![]() jacobi_elliptic_specified_point_Passing_straight_line_tangent_to_a_curve.zip
jacobi_elliptic_specified_point_Passing_straight_line_tangent_to_a_curve.zip