縄跳び紐の接線その１
縄跳び紐の形状に対して、傾きαを指定した接線の計算をします。
ヤコビ関数ｓｎ(ｚ)を微分して、傾きαの値から縄跳び紐との接点座標を求める事が出来ますが、それに先立って、縄飛び紐の曲線を細かく分割して、傾斜α’とＸ座標の配列を作成し、その配列から指定された傾斜αに対する、座標を割り出すプログラムを作成しました。
α’＝Δｙ／Δx
直線の
傾斜αの値が、配列の中間の値の場合は、補完法を使用して計算します。
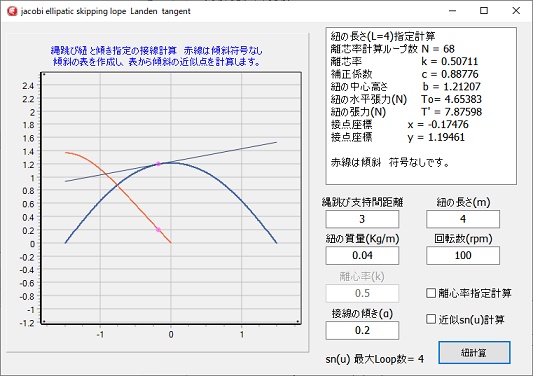左図赤線が傾斜α’の値で絶対値の値です。
縄跳び紐の曲線の中央で、傾斜α’はゼロになります。
直線の傾斜αにマイナスの値を指定しても、赤の傾斜のグラフは変わりません。
前に作成したプログラムに接線の計算を追加したので、張力や長さ指定計算が残っています。
sn(u,k)の計算は、am(Φ)による計算と、第一種楕円積分F(x,k)により近似計算をするルーチンが入っています。
近似計算といっても、1E-12の判定値としているので、結構精度の高い結果が得られます。
紐の曲線の傾斜α’の値は紐の端点が一番大きくなるので、端点の値を超える傾斜の接線は無いことになります。
sn(u)数は、am(Φ)内のループ数
又は、一回のsn計算時の第一種楕円積分計算回数を示していますので、第一種楕円積分計算使用時はam(Φ)利用時に対して何百倍計算をしています。
プログラム
楕円積分は、離心率kが１以下なら積分範囲に制限が無い計算を使用しています。
積分範囲をpi/2に制限すれば、楕円積分のプログラムは短く出来ます。
他のプログラムで、同じ様に楕円積分を使用していますが、プログラムによって、違う方式の楕円積分計算を使用しているものがあるので参考にして下さい。
//----------------------------------------------------- // ヤコビの楕円関数と縄跳びの紐計算 // http://fuchino.ddo.jp/yatsugatake/ellipticx.pdf // http://www.wannyan.net/scidog/ellipse/ellipse.pdf //----------------------------------------------------- unit Main; interface uses Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics, Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls, VclTee.TeeGDIPlus, VCLTee.TeEngine, VCLTee.Series, VCLTee.TeeProcs, VCLTee.Chart; type TForm1 = class(TForm) LabeledEdit10: TLabeledEdit; LabeledEdit11: TLabeledEdit; Memo1: TMemo; nawaBtn: TButton; Chart1: TChart; Series1: TLineSeries; Series2: TPointSeries; massEdit: TLabeledEdit; rotational_speed_Edit: TLabeledEdit; LabeledEdit1: TLabeledEdit; CheckBox1: TCheckBox; Label1: TLabel; LabeledEdit2: TLabeledEdit; Series3: TLineSeries; Series4: TPointSeries; Series5: TLineSeries; CheckBox2: TCheckBox; procedure nawaBtnClick(Sender: TObject); procedure FormCreate(Sender: TObject); procedure CheckBox1Click(Sender: TObject); procedure CheckBox1KeyPress(Sender: TObject; var Key: Char); private { Private 宣言 } function calc_first_elliptic_integral(k, sinQ: double): double; function calc_second_elliptic_integral(k, sinQ: double): double; function jacobi_sn(u, k: double): double; procedure tension(a2, k, b, c: double); function invertK(L, a2: double): double; function second_imperfect_elliptic_integral(Q, K: double; F: integer): double; procedure tangent(a2, k, b, c, alpha, ty: double); function L_jacobi_sn(u, k: double): double; public { Public 宣言 } end; var Form1: TForm1; implementation {$R *.dfm} uses System.Math; var V : integer; // 反復計算ループ数 DBL_EPSILON : double; //------------------------------- // 第１種第２種不完全積分 // FBnKn[0] 第１種不完全積分解 // EBnKn[0] 第２種不完全積分解 // ランデン変換 // Q 角度 rad // K 離心率 // F = 1 第一種積分 F <> 1 第二種積分 //------------------------------- function TForm1.second_imperfect_elliptic_integral(Q, K: double; F: integer): double; var I, MI : integer; Kn : array of double; // Kn knd : array of double; // k'n N2SKn : array of double; // 2/(1+Kn) T2SKnd : array of double; // П2/(1+Kn') BRad : array of double; // β(rad) SinBn : array of double; // sinβn FBnKn : array of double; // F(βn,kn) EBnKn : array of double; // E(βn,kn) LnD : double; begin // K = 0 の時は円なのでpiの角度値rad。 if K = 0 then begin result := Q; exit; end; // この時は1をかえします。 if (F <> 1) and (K >= 1) and (Q >= pi / 2) then begin // F <> 1 は第二種積分 result := 1; exit; end; // 1 >= K > 0 の時 MI := 0; LnD := 0; setlength(kn, MI + 1); // kn kn[0] := K; while LnD <> Kn[MI] do begin // LnDとkn[]が同じ１になるまでくり返します LnD := Kn[MI]; inc(MI); setlength(kn, MI + 1); // kn kn[MI] := 2 * sqrt(Kn[MI - 1])/(1 + Kn[MI - 1]); end; setlength(kn, MI); // kn setlength(knd, MI); // k'n setlength(N2SKn, MI); // 2/(1+Kn) setlength(T2SKnd, MI); // П2/(1+Kn') setlength(BRad, MI); // β(rad) setlength(SinBn, MI); // sinβn setlength(FBnKn, MI); // F(βn,kn) setlength(EBnKn, MI); // E(βn,kn) dec(MI); knd[0] := 1; for I := 1 to MI do knd[I] := (1 - kn[I - 1]) / (1 + Kn[I - 1]); for I := 0 to MI do N2SKn[I] := 2 / (1 + kn[I]); T2SKnd[MI] := N2SKn[MI]; for I := MI - 1 downto 0 do T2SKnd[I] := T2SKnd[I + 1] * N2SKn[I]; BRad[0] := Q; for I := 1 to MI do BRad[I] := (arcsin(kn[I - 1] * sin(Brad[I - 1])) + Brad[I - 1]) / 2; for I := 0 to MI do SinBn[I] := sin(Brad[I]); result := (1 + sin(Brad[MI])) / cos(Brad[MI]); if result <= 0 then exit; // 0以下は自然対数の計算出来ません LnD := Ln(result); if F = 1 then begin // 第一種指定なら result := T2SKnd[0] * LnD; // 第一種 exit; end; for I := 0 to MI do FBnKn[I] := T2SKnd[I] * LnD; EBnKn[MI] := sin(Brad[MI]); for I := MI - 1 downto 0 do EBnKn[I] := (2 * EBnKn[I + 1] + 2 * knd[I + 1] * FBnKn[I + 1]) / (1 + knd[I + 1]) - kn[I] * SinBn[I]; result := EBnKn[0]; // 第二種 end; // 第一種楕円積分 ルーチン // 積分範囲制限なし sin(θ) 単位 function TForm1.calc_first_elliptic_integral(k, sinQ: double): double; var J : integer; fqk : double; f1k : double; fek : double; asin : double; begin asin := abs(sinQ); if (k >= 1) and (asin >= 1) then begin // 積分出来ない値だったら if sinQ > 0 then result := MaxDouble // double最大値セット∞の代わり else result := -MaxDouble; // double最小値セット-∞の代わり exit; // 終了 end; f1k := 0; // 完全積分値初期化 J := trunc(asin); // 整数部取り出し if J mod 2 = 0 then asin := asin - J // 小数部処理 象限処理 else asin := 1 - (asin - J); if (J <> 0) and (k < 1) then f1k := second_imperfect_elliptic_integral(pi / 2, K, 1); // 第一種完全積分 fek := second_imperfect_elliptic_integral(arcsin(asin), K, 1); // 第一種不完全積分 if j mod 2 = 0 then fqk := j * f1k + fek // 第1,第3象限の積分値 else fqk := (j + 1) * f1k - fek; // 第2,第4象限の積分値 if sinQ < 0 then fqk := -fqk; // 積分範囲の符号で積分値の符号設定 result := fqk; end; // 第二種楕円積分 ルーチン // 積分範囲 制限なし rad 単位 function TForm1.calc_second_elliptic_integral(k, sinQ: double): double; var f1e : double; eek ,ek : double; j : integer; asin : double; begin asin := abs(sinQ); j := trunc(asin); // 整数部取り出し if j mod 2 = 0 then asin := asin - j // 小数部処理 象限処理 else asin := 1 - (asin - j); if (j <> 0) and (k < 1) then begin f1e := second_imperfect_elliptic_integral(pi / 2, K, 2); // 第二種完全積分 end else f1e := 1; if k < 1 Then ek := second_imperfect_elliptic_integral(arcsin(asin), K, 2) // 第二種不完全積分 else ek := asin; if j mod 2 = 0 then eek := j * f1e + ek // 第1,第3象限の積分値 else eek := (j + 1) * f1e - ek; // 第2,第4象限の積分値 if sinQ < 0 then eek := -eek; // 積分範囲の符号で積分値の符号設定 result := eek; end; // Jacobi関数 Jacobi sn(u, k) function TForm1.Jacobi_sn(u, k: double): double; const KN = 30; var a: array of double; g: array of double; c: array of double; two_n : double; phi : double; half : double; i, j, N : integer; begin half := 1 / 2; if k = 0 then begin result := sin(u); exit; end; if k = 1 then begin result := sin(2 * arctan(exp(u)) - pi / 2); exit; end; N := 1; setlength(a, N); setlength(g, N); setlength(c, N); a[0] := 1; g[0] := sqrt(1 - k * k); c[0] := k; two_n := 1; for i := 0 to KN do begin if abs(a[i] - g[i]) < a[i] * DBL_EPSILON then break; two_n := two_n + two_n; inc(N); setlength(a, N); setlength(g, N); setlength(c, N); a[i + 1] := half * (a[i] + g[i]); g[i + 1] := sqrt(a[i] * g[i]); c[i + 1] := half * (a[i] - g[i]); end; V := i; // ループ数表示用 phi := two_n * a[i] * u; for j := i downto 1 do phi := half * (phi + arcsin(c[j] * sin(phi) / a[j])); result := sin(phi); end; // ヤコビの楕円関数 sn(u, k) // 第一種楕円積分によりsn(u)の近似値計算 function TForm1.L_jacobi_sn(u, k: double): double; const KN = 1000; var sinQ : double; bsinQ : double; ud, dsin : double; i : integer; absu : double; begin absu := abs(u); // uの絶対値 dsin := 0.25; // 初期補正角度設定 sinQ := 0.25; // 初期値設定 for i := 0 to KN do begin ud := calc_first_elliptic_integral(k, sinQ); // 第一種楕円積分 if abs(ud - absu) < max(ud, absu) * DBL_EPSILON then break; // 積分値と指定値の差が誤差設定値より小さくなったら終了 if ud > absu then begin // 積分値が指定値より大きかったら sinQ := sinQ - dsin; // 補正値減算 dsin := dsin / 2; // 補正値２分の１に end; bsinQ := sinQ; sinQ := sinQ + dsin; // 補正値加算 if sinQ = bsinQ then break; // 角度補正値が収束判定値より小さくなったら終了 end; if V < i then V := i; // ループ数表示用 i := trunc(sinQ); if i mod 2 = 0 then // sin(90°)単位をsin(180°)単位に変換 sinQ := (sinQ - i) // 奇数象限と偶数象限計算 else sinQ := 1 - (sinQ - i); i := i div 2; // sin(180°)単位をsin(360°)に変換 if i mod 2 <> 0 then sinQ := -sinQ; // sinは180°毎符号が反転 if u < 0 then sinQ := -sinQ; // 範囲の符号で逆変換値の符号設定 result := sinQ; end; // 傾きを指定された直線の接点位置の計算 // 紐のx方向に対する曲線の傾斜のデーター配列を作成し、直線の傾斜角に近い値xの値を算出します。 // 補完法を使用して、正解に近づけます // a2 縄跳びの支持間距離 // k 離心率 // b 縄跳び紐の高さ // c 曲線係数 // alpha 傾斜 // ty グラフ上限値 procedure TForm1.tangent(a2, k, b, c, alpha, ty: double); const KN = 2000; var i : integer; dx, u, snuk : double; a, x, y, yb : double; dy, t, dx2 : double; xi, ti : array of double; absa, z : double; begin absa := abs(alpha); setlength(xi, KN + 2); setlength(ti, KN + 2); // xと傾きの関係グラフ作図と配列データー作成 a := a2 / 2; yb := 0; dx := a / KN; dx2 := dx / 2; xi[0] := 0; // 0の位置 ti[0] := b / c; // 0の位置の傾斜 Series3.AddXY(xi[0] - a, ti[0]); // グラフに追加 for i := 1 to KN do begin x := i * dx; // x位置 u := x / c; // F(α,k)=u if checkbox2.Checked then snuk := L_jacobi_sn(u, k) else snuk := jacobi_sn(u, k); // jacobi_sn ヤコビの楕円関数 y := snuk * b; // x位置のyの値 dy := y - yb; // y差分 yb := y; // y -> yb t := dy / dx; // 傾き xi[i] := x - dx2; // 配列にx座標 xは中間位置 ti[i] := t; // 配列に傾き Series3.AddXY(xi[i] - a, t); // グラフに追加 end; xi[KN + 1] := a; // aの位置 ti[KN + 1] := 0; // aの位置の傾斜はゼロ Series3.AddXY(0, 0); // グラフに追加 application.ProcessMessages; // 直線の傾きからxの値計算補完法 for i := KN downto 0 do begin if absa <= ti[i] then begin t := ti[i]; // x位置の傾きの値 dy := absa - t; // 差分 dy := dy / (ti[i + 1] - t); // 差分比 x := xi[i]; // xの値 dx := xi[i + 1] - x; // xの範囲 dx x := x + dx * dy; // 補完計算 Series4.AddXY(x - a, absa); // グラフに位置追加 break; end; end; u := x / c; // F(α,k)=u if checkbox2.Checked then snuk := L_jacobi_sn(u, k) else snuk := jacobi_sn(u, k); // jacobi_sn ヤコビの楕円関数 y := snuk * b; // x位置のyの値 if alpha < 0 then x := a2 - x; // 傾きがマイナスの場合はxが逆方向 Series4.AddXY(x - a, y); // グラフに接点の位置追加 x := x - a; // xを中心座標に変換 memo1.Lines.Add('接点座標 x = ' + floatTostrF(x, ffFixed, 10, 5)); memo1.Lines.Add('接点座標 y = ' + floatTostrF(y, ffFixed, 10, 5)); // 直線の描画 z := y - alpha * x; // 切片の計算 dx := 0 - a; // 始点x dy := alpha * dx + z; // 始点y if dy > ty then begin // yの値がグラフの上限を超えたら調整 dx := (ty - z) / alpha; dy := ty; end; Series5.AddXY(dx, dy); // グラフに追加 dx := a2 - a; // 終点x dy := alpha * dx + z; // 終点y if dy > ty then begin // yの値がグラフの上限を超えたら調整 dx := (ty - z) / alpha; dy := ty; end; Series5.AddXY(dx, dy); // グラフに追加 end; // 紐の張力、長さ 計算 // a2 縄跳びの支持間距離 // k 離心率 // b 縄跳び紐の高さ // c 曲線係数 procedure TForm1.tension(a2, k, b, c: double); const KN = 1000; var ch : integer; p, w : double; R, T : double; T0, g : double; Ke : double; begin val(massEdit.Text, p, ch); if ch <> 0 then begin application.MessageBox('紐の質量に間違いがあります。','注意', 0); exit; end; if p < 0 then begin application.MessageBox('紐の質量にマイナスはありません。','注意', 0); exit; end; val(rotational_speed_Edit.Text, R, ch); if ch <> 0 then begin application.MessageBox('回転数に間違いがあります。','注意', 0); exit; end; w := R / 60 * pi * 2; // 角速度 ω g := p * w * w; // γ=ρ*ω^2 Ke := calc_first_elliptic_integral(k, 1); // 第一種完全積分 T0 := g * a2 * a2 / 4 / (1 - k * k) / Ke / Ke; memo1.Lines.Add('紐の水平張力(N) To= ' + floatTostrF(T0, ffFixed, 10, 5)); T := T0 * sqrt(b * b / c / c + 1); memo1.Lines.Add('紐の張力(N) T'' = ' + floatTostrF(T, ffFixed, 10, 5)); end; // 離芯率kの計算 // L=4a/k'^2*E/K-2aのaとLが既知なのでkの値を求めます。 // L 紐の長さ // a2 支持間距離 function TForm1.invertK(L, a2: double): double; var c, fc : double; k, E, fk : double; dk : double; N : integer; bk : double; begin a2 := abs(a2); c := (L + a2) / a2 / 2; // L=4a/k'^2*E/K-2a から判定用固定値計算 dk := 1 / 2; // Δk k := dk; // 離心率初期値 N := 0; repeat inc(N); if k >= 1 then k := 1 - DBL_EPSILON; // kが1に成った時1から僅かに小さくします。 E := calc_second_elliptic_integral(k, 1); // 第二種完全積分 fk := calc_first_elliptic_integral(k, 1); // 第一種完全積分 fc := E / fk / (1 - k * k); // 判定比較値計算 if fc > c then begin // 大きかったら k := k - dk; // Δk減算 dk := dk / 2; // Δk 2分の1 end; bk := k; k := k + dk; // k+Δk until (k = bk) or (N > 200); // 収束判定 memo1.Lines.Add('離芯率計算ループ数 N = ' + intTostr(N)); result := k; end; // 縄跳びの縄弛み計算 procedure TForm1.nawaBtnClick(Sender: TObject); const kN = 400; var k : double; ch : integer; a, a2 : double; fkd, b, u : double; c, L : double; i : integer; x, y, dx : double; snuk : double; ty, by : double; lx, rx : double; def, ddf : double; Ek : double; Lk : double; alpha : double; Vm : double; begin V := 0; k := 0; L := 0; val(Labelededit10.Text, a2, ch); if ch <> 0 then begin application.MessageBox('縄跳び紐支持間に間違いがあります。','注意',0); exit; end; val(Labelededit2.Text, alpha, ch); if ch <> 0 then begin application.MessageBox('直線の傾きに間違いがあります。','注意',0); exit; end; if checkbox1.Checked then begin val(LabeledEdit1.Text, k, ch); if ch <> 0 then begin application.MessageBox('縄跳び紐離心率Ｋに間違いがあります。','注意',0); exit; end; if k > 1 then begin application.MessageBox('k(離心率)の最大値は１です。','注意',0); exit; end; if k < 0 then begin application.MessageBox('k(離心率)の値にマイナスはありません。','注意',0); exit; end; end else begin val(LabeledEdit11.Text, L, ch); if ch <> 0 then begin application.MessageBox('縄跳び紐の長さに間違いがあります。','注意',0); exit; end; if L <= abs(a2) then begin application.MessageBox('紐の長さは支持間より長くしてください。','注意',0); exit; end; end; memo1.Clear; if not checkbox1.Checked then begin memo1.Lines.Add('紐の長さ(L=' + floatTostr(L) + ')指定計算'); k := invertK(L, a2); // 離芯率kの計算 memo1.Lines.Add('離芯率 k = ' + floatTostrF(k, ffFixed, 10, 5)); end else memo1.Lines.Add('離心率(k=' + floatTostr(k) + ')指定計算'); fkd := calc_first_elliptic_integral(k, 1); // 第一種完全積分 if abs(k) = 1 then begin application.MessageBox('離心率の絶対値が１です１以下にして下さい。','注意',0); exit; end; if abs(k) = 0 then begin application.MessageBox('離心率がゼロです。','注意',0); exit; end; // 各種計算 a := a2 / 2; c := a / fkd; // 積分値に対する補正係数 b := 2 * k / (1 - k * k) * c; // 最大値 中央の位置 if abs(alpha) > (b / c) then begin application.MessageBox(pchar('直線の傾斜が大きすぎます。' + #13#10 + '最大値は' + floatTostr(b/c) + ' です。'),'注意',0); exit; end; memo1.Lines.Add('補正係数 c = ' + floatTostrF(c, ffFixed, 10, 5)); memo1.Lines.Add('紐の中心高さ b = ' + floatTostrF(b, ffFixed, 10, 5)); // 紐の長さ計算 中間位置の計算は出来ません if checkbox1.Checked then begin Ek := calc_second_elliptic_integral(k, 1); // 第二種完円積分 Lk := 4 * c * Ek / (1 - k * k) - a2; // 弧の長さ計算 memo1.Lines.Add('紐の長さ L = ' + floatTostrF(Lk, ffFixed, 10, 5)); end; Series1.Clear; Series2.Clear; Series3.Clear; Series4.Clear; Series5.Clear; // グラフスケール設定 Vm := b / c; if b > Vm then Vm := b; if abs(a2) > Vm then begin ddf := a2 / 10; def := (a2 - b) / 2; ty := Vm + def + ddf; by := 0 - def - ddf; rx := a + ddf; lx := -a - ddf; end else begin ddf := Vm / 10; def := (Vm - a2) / 2; ty := Vm + ddf; by := 0 - ddf; rx := a + def + ddf; lx := -a - def - ddf; end; // グラフのスケール設定値セット Series2.AddXY(lx, ty); Series2.AddXY(lx, by); Series2.AddXY(rx, by); application.ProcessMessages; // グラフ作図 dx := a2 / KN; // ΔX // 0～KN 計算作図 for i := 0 to KN do begin x := i * dx; // x位置 u := x / c; // F(α,k)=u if checkbox2.Checked then snuk := L_jacobi_sn(u, k) else snuk := jacobi_sn(u, k); // jacobi_sn ヤコビの楕円関数 y := snuk * b; // x位置のyの値 Series1.AddXY(x - a, y); // グラフに追加 end; application.ProcessMessages; // 張力計算 tension(a2, k, b, c); tangent(a2, k, b, c, alpha, ty); Label1.Caption := 'sn(u) 最大Loop数= ' + intTostr(V); memo1.Lines.Add(''); memo1.Lines.Add('赤線は傾斜 符号なしです。'); end; procedure TForm1.CheckBox1Click(Sender: TObject); begin if CheckBox1.Checked then begin labeledEdit1.Enabled := True; labeledEdit11.Enabled := False; end else begin labeledEdit1.Enabled := False; labeledEdit11.Enabled := True; end; end; procedure TForm1.CheckBox1KeyPress(Sender: TObject; var Key: Char); begin if CheckBox1.Checked then CheckBox1.Checked := False else CheckBox1.Checked := True; end; procedure TForm1.FormCreate(Sender: TObject); var x, y, z : double; i : integer; begin i := 0; x := 1; y := 1; repeat y := y / 2; z := x + y; inc(i); until (z = x) or (i > 100); DBL_EPSILON := y * 2; labeledEdit1.Enabled := False; end; end.
Jacobi_elliptic_skipping_rope_tangent.zip