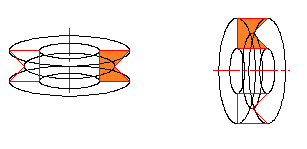
断面形状を入力することにより、その断面が回転して出来る回転体の慣性モーメントを計算します。
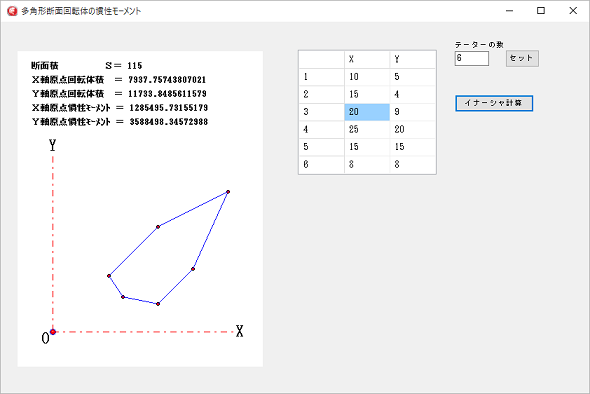 データーの数をセット後、多角形頂点の座標を反時計回りに入力します。
データーの数をセット後、多角形頂点の座標を反時計回りに入力します。計算結果は、密度を1として、計算されます。
実際の慣性モーメントは此処で計算された結果に、密度を乗じる必要があります。
平面多角形の慣性モーメントの場合は、単位面積当たりの質量でしたが、此処では、単位体積の密度を使用します。
座標値はX、Yとも、マイナスの値を入力してはいけません。
回転体の断面なので、マイナスの座標値はありません。
多角形断面を持つ回転体の慣性モーメント

断面形状を入力することにより、その断面が回転して出来る回転体の慣性モーメントを計算します。
 データーの数をセット後、多角形頂点の座標を反時計回りに入力します。
データーの数をセット後、多角形頂点の座標を反時計回りに入力します。
計算結果は、密度を1として、計算されます。
実際の慣性モーメントは此処で計算された結果に、密度を乗じる必要があります。
平面多角形の慣性モーメントの場合は、単位面積当たりの質量でしたが、此処では、単位体積の密度を使用します。
座標値はX、Yとも、マイナスの値を入力してはいけません。
回転体の断面なので、マイナスの座標値はありません。
計算方法は、意外と簡単で、座標2点のX軸又はY軸からの距離を円錐台の半径として、慣性モーメントを計算します。
体積計算時、回転体の内側の体積がマイナスになるようにして、慣性モーメントを計算し、多角形を一周計算し、合計を求めれば、慣性モーメントが計算されます。
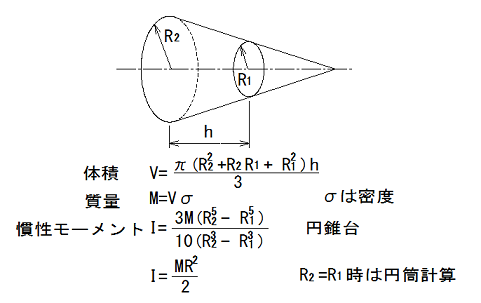
例えば X軸の慣性モーメントは、まず、体積を求めます、 R1 R2
はYn Yn+1 とし、h
は Xn+1-Xnとして計算します。
次に、慣性モーメントを計算します。
質量Mは、体積に密度を乗じますが、ここでは、密度を1としてけいさんしています。
R1=R2の時は、円錐台としての計算が出来ないので、円柱の計算を使用します。
計算結果に、密度を乗ずれば、本来の慣性モーメントになります。
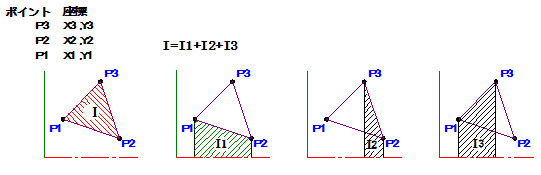
上図三角形の場合、I1がマイナスになり、I2,I3はプラスになります。
合計を求めると、三角形断面回転体の慣性モーメント I
となります。(面積の計算の場合と同じです。)
計算プログラム部 (累乗計算のPower(X.a)は使用は使用しないでプログラムしました)
X軸とY軸では、合計計算時慣性モーメントの符号が反対になるので注意が必要です。
// イナーシャ計算 procedure TForm1.Inertia_Calc; // 慣性モーメント計算 var HX, HY : double; // 高さ VX, VY : double; // 体積 SVX, SVY : double; X1, X2, Y1, Y2 : double; I : Integer; begin IX := 0; IY := 0; // 慣性モーメント SVX := 0; SVY := 0; // 全体積 X2 := Xd[N - 1]; Y2 := Yd[N - 1]; // 最後のデーターセット for I := 0 to N - 1 do begin // 座標点反時計回り計算 X1 := X2; Y1 := Y2; X2 := Xd[I]; Y2 := Yd[I]; HX := X2 - X1; // X差分 HY := Y2 - Y1; // Y差分 VX := (Y1 * Y1 + Y1 * Y2 + Y2 * Y2) * HX * pi / 3; // 体積 V = (R^2 + R*r + r^2 * h) * pi / 3 VY := (X1 * X1 + X1 * X2 + X2 * X2) * HY * pi / 3; if Y2 <> Y1 then // Y方向の半径に差が有ったら円錐台計算 IX := IX - (Y2 * Y2 * Y2 * Y2 * Y2 - Y1 * Y1 * Y1 * Y1 * Y1) / // X軸慣性モーメント I = 3(R^5 - r^5)/(R^3 - r^3) * m / 10 (Y2 * Y2 * Y2 - Y1 * Y1 * Y1) * VX * 3 / 10 else // 同じ値だったら円筒計算 IX := IX - Y2 * Y2 * VX / 2; // I = R^2 * m / 2 if X2 <> X1 then // X方向の半径に差が有ったら円錐台計算 IY := IY + (X2 * X2 * X2 * X2 * X2 - X1 * X1 * X1 * X1 * X1) / // Y軸慣性モーメント I = 3(R^5 - r^5)/(R^3 - r^3) * m / 10 (X2 * X2 * X2 - X1 * X1 * X1) * VY * 3 / 10 else // 同じ値だったら円筒計算 IY := IY + X2 * X2 * VY / 2; // I = R^2 * m / 2 SVX := SVX - VX; // 全体積計算 SVY := SVY + VY; // 全体積計算 end; with Image1 do begin Canvas.Font.Height := 12; Canvas.TextOut(20,35, 'X軸原点回転体積 = ' + floatTostr(SVX)); Canvas.TextOut(20,55, 'Y軸原点回転体積 = ' + floatTostr(SVY)); Canvas.TextOut(20,75, 'X軸原点慣性モーメント = ' + floatTostr(IX)); Canvas.TextOut(20,95, 'Y軸原点慣性モーメント = ' + floatTostr(IY)); end; end;