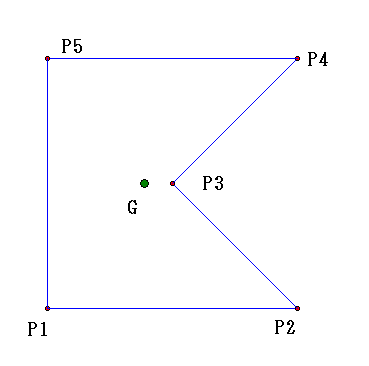
多角形平面多角形の慣性モーメント

平面多角形の面積を求めるプログラムに慣性モーメントを求める計算を追加してみました。

　座標の入力や、入力ミスの確認は、面積の計算と全く同じで、慣性モーメントの計算には、面積を求める必要があるので、慣性モーメントを求める計算プログラムがあれば、単純に面積だけを求めるプログラムは、不要となります。

此処での慣性モーメントの計算は、単位面積の質量を １ として計算しています。
本来の慣性モーメントを求める場合は、単位面積当たりの質量を入力する項目を追加し、此処で計算された面積から全質量を計算し、計算された慣性モーメントに、乗算して下さい。

座標の入力は、反時計回りです、時計回りに計算する場合は、計算式の変更が必要です。


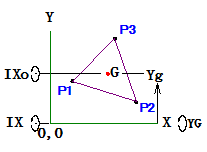三角形の例１　慣性モーメントは、図形の重心を中心として回転する慣性モーメントと、座標原点を通る軸に対しての図形重心が回転する慣性モーメントがあり、両方を加算したものが座標原点を通る軸にたいする慣性モーメントです。
此処での計算では、座標原点を通る軸に対しての慣性モーメントを計算し、重心を通る軸に対する慣性ﾈｰﾒﾝﾄは、重心が座標原点軸に対する慣性モーメントを計算し、前記慣性モーメントから差し引いて、重心を通る軸の慣性モーメントを計算しています。
Ｘ軸に対する慣性モーメントＩＸとＹ軸に対する慣性モーメントＩＹを加算したものが、Ｚ軸に対する慣性モーメントＩＺとなります。
　左図は、Ｘ軸方向に対する慣性モーメントを表しています。

面積の計算と同じように、三角形の慣性モーメントを考えて見ます。

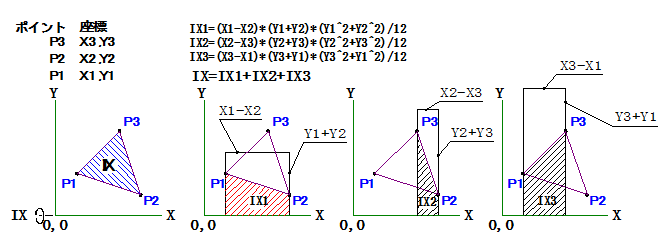
 慣性モーメント計算0
　慣性モーメントの計算は、面積と同じで、上図ハッチング部分の慣性モーメントを計算し、総和を求めて慣性モーメントとします。
計算式は、座標原点を通るＸ軸にたいする慣性モーメントです。
X1-X2がマイナスになるのは、上図赤ハッチングの部分で、全部を加算すると、三角形部分の慣性モーメントとなります。
Ｙ軸に対しての慣性モーメントは、Ｙ軸を基準に計算式を変更すれば良いのですが、単にＸ１－Ｘ２をＹ１－Ｙ２にすると、差分の値の符号が反対になるので、Ｙ２－Ｙ１にする必要があります。
此処での計算は、反時計回りとなっていますが、これは、座標系は全て反時計回りに定義されているからです。
もし、時計回りに計算する場合は、差分（Ｘ１－Ｘ２）を逆（Ｘ２－Ｘ１）にすれば、良い事になります。

　重心位置の計算
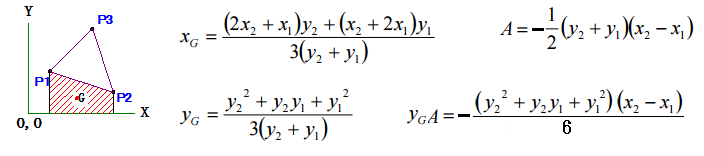
重心を通る軸の慣性モーメント
　上図は、反時計回りの最初の計算を表しています。
Ａは斜線部分の面積です、マイナスの符号は、上図の場合減算する面積だからです、（Ｘ１－Ｘ２）にすればマイナスの符号は要りません。
慣性モーメント（二次モーメント）の計算と同じで、ＹＧＡ （一次モーメント） を計算し、全てを加算後、三角形面積で除算をすると、原点を通る軸からの三角形重心Ｇ迄の距離を求める事が出来ます。

重心Ｇを通るＸ軸に対する慣性モーメントは　ＩＸ－ＹＧ２Ａとなります。
上図のＸＧの計算式は、本プログラムでは利用していません、Ｙ軸に対する慣性モーメント計算を軸を入れ替えることによって行っているので、ＹＧの計算式のＹをＸに入れ替えることによって、ＸＧの計算をしています。

次のプログラム例は、面積を求めるプログラムに対して、慣性モーメントを求める部分を追加したので、その追加ルーチンです。

 var
  XG, YG     : double;        // 重心位置
  IX, IY, IZ : double;        // 慣性モーメント


// イナーシャ計算
procedure TForm1.Inertia_Calc;                   // 慣性モーメント計算
var
  DX, DY          : double;
  X1, X2, Y1, Y2  : double;
  SX, SY          : double;
  I               : Integer;
  IXo, IYo, IZo   : Double;
  Xp, Yp          : Integer;
begin
  SX := 0; SY := 0;         // 面積
  XG := 0; YG := 0;         // 重心位置
  IX := 0; IY := 0;         // 慣性モーメント

  X2 := Xd[N - 1]; Y2 := Yd[N - 1]; // 最後のデーターセット

  for I := 0 to N - 1 do begin
    X1 := X2;
    Y1 := Y2;
    X2 := Xd[I];
    Y2 := Yd[I];
    DX := X2 - X1;                                        // X差分
    DY := Y2 - Y1;                                        // Y差分
    SX := SX - DX * (Y1 + Y2) / 2;                        // 面積計算 SXとSYは同じ値と成ります
    SY := SY + DY * (X1 + X2) / 2;                        // 面積計算
    XG := XG + DY * (X1 * X1 + X1 * X2 + X2 * X2) / 6;    // 一次モーメントX 最後に全面積で除算します
    YG := YG - DX * (Y1 * Y1 + Y1 * Y2 + Y2 * Y2) / 6;    // 一次モーメントY 最後に全面積で除算します
    IX := IX - DX * (Y1 + Y2) * (Y1 * Y1 + Y2 * Y2) / 12; // Ｘ軸慣性モーメント
    IY := IY + DY * (X1 + X2) * (X1 * X1 + X2 * X2) / 12; // Ｙ軸慣性モーメント
  end;
  XG := XG / SX;                                          // 面積で除算し重心位置にする
  YG := YG / SY;                                          // 面積で除算し重心位置にする
  IZ := IX + IY;                                          // Ｚ軸慣性モーメント
  IXo := IX - YG * YG * SY;                               // 重心を通るＸ軸慣性モーメント
  IYo := IY - XG * XG * SX;                               // 重心を通るＹ軸慣性モーメント
  IZo := IXo + IYo;                                       // 重心を通るＺ軸慣性モーメント
  with Image1 do begin
//    Canvas.TextOut(20,50,  'SX='  + floatTostr(SX));
//    Canvas.TextOut(20,70,  'SY=' + floatTostr(SY));
    Canvas.TextOut(20,40,  '重心位置　      Ｘ＝ ' + floatTostr(XG));
    Canvas.TextOut(20,60,  '重心位置        Ｙ＝ ' + floatTostr(YG));
    Canvas.TextOut(20,80,  'Ｘ軸慣性モーメント＝ ' + floatTostr(IXo));
    Canvas.TextOut(20,100, 'Ｙ軸慣性モーメント＝ ' + floatTostr(IYo));
    Canvas.TextOut(20,120, 'Ｚ軸慣性モーメント＝ ' + floatTostr(IZo));
    Canvas.TextOut(20,145, 'Ｘ軸原点慣性ﾓｰﾒﾝﾄ ＝ ' + floatTostr(IX));
    Canvas.TextOut(20,165, 'Ｙ軸原点慣性ﾓｰﾒﾝﾄ ＝ ' + floatTostr(IY));
    Canvas.TextOut(20,185, 'Ｚ軸原点慣性ﾓｰﾒﾝﾄ ＝ ' + floatTostr(IZ));
  end;
  Xp :=  50 + Round((XG - Xmin) * Scale);      // Xの位置計算
  Yp := 550 - Round((YG - Ymin) * Scale) - 50; // Yの位置計算
  Image1.Canvas.Pen.Color := clBlack;
  Image1.Canvas.Brush.Color := clGreen;
  Image1.Canvas.Ellipse(Xp - 4, Yp - 4, Xp + 5, Yp + 5);  // 円を描画中を塗りつぶし
end;


　　　　　　　　download　Polygon_Inertia．ｚｉｐ


　　　　　　　　各種プログラム計算例に戻る