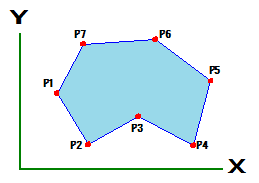
座標点Pのn点であらわされる多角形の面積は、
但し、Xn+1=X1,Yn+1=Y1
カッコの部分を書き直すと、 XkYk-Xk+1Yk+XkYk+1-Yk+1Xk+1 となります。
XkYk-Yk+1Xk+1の部分のシグマの値は、ゼロになるので
多角形の面積

座標点Pのn点であらわされる多角形の面積は、
![]() で計算されます。
で計算されます。
但し、Xn+1=X1,Yn+1=Y1
カッコの部分を書き直すと、 XkYk-Xk+1Yk+XkYk+1-Yk+1Xk+1 となります。
XkYk-Yk+1Xk+1の部分のシグマの値は、ゼロになるので
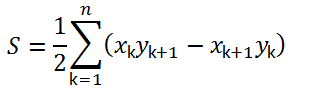
となります。(外積による計算と同じ)
左回りに座標を入れ計算するのか、右回りで計算するのかで、値がマイナスとなるので、どちら周りで計算しても良いように絶対値をとって
![]()
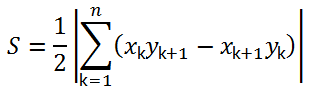
プログラム上で計算するので、どちらで計算しても良いでしょう。
外積については、イメージングソリューションに詳しい説明が載っているので参照して下さい。
最初の計算式についての検討。
面積を持つ多角形で一番座標点が少ないのは、三角形なので三角形について検討します。
座標点を結ぶ二点の直線の下側部分X軸までの、面積を計算します。
X座標の差分と、Y座標を加算した値の積を二分の一にすると、その面積が計算できます。
全ての辺について、一周計算し、面積の合計値を計算すれば、三角形部分の面積となります。
今回の例では、左回りに計算すると、面積は正の値となり、右回りに計算すると、負の値になります。
(Y軸方向に面積を計算する場合は、Y座標の差分と、X座標の加算をとります。)
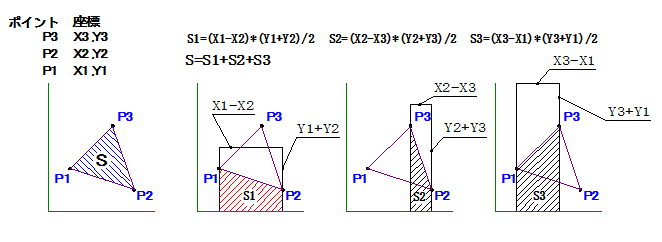
面積S1の値はマイナスになるので、面積Sは、S=S1+S2+S3 となるのは、上図をみれば、あきらかです。
座標点を結ぶ直線が交差しない限り、座標点が増えても、計算式が成り立ちます。
計算プログラム使用時の座標入力時の注意点
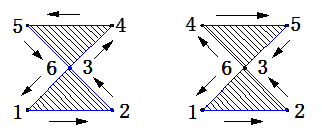
上図の様に同じ座標を通る図形がある場合、左図の様に図形上を同じ方向に回るように入力します。
右図のように入力すると、上の三角形部と、下の三角形部で入力方向が逆方向になってしまい、正しく計算されません。
上の三角形と、下の三角形を別々に計算したほうが、間違いを防ぐことが出来るでしょう。
同じ座標点があったら、入力ミスとすれば良いのですが、此処でのプログラムでは簡単なので省略しています。
此処でダウンロード出来るサンプルプログラムでは、ある程度の座標値の入力ミスのチェックをしていますが、入力方向(左回り右回り)の確認はしていません。
入力ミスの判定は次の様におこないます。

上図A~Eの場合は問題なしとし、F~Hの様な場合、辺の交差ありとしています。

最初の辺交差の確認では、三点による連続線に対して、中間点が、他の辺の線上からずれている場合は良いのですが、線上にある場合正しく判定出来ません。
そこで、この場合に対する判定を行います。
まず、三点の中間点cの点が、辺Klの線上にあるか判断します。
線上にあると判断したら、辺klの角度から辺klが水平で、c点が座標が原点0,0になるように座標変換します。

上図Aの場合は、三点による連続線の両端が、プラスY側とマイナスY側に分かれているので、辺が交差していると判断します。
B~Fの場合は交差なしとします。
辺の交差があると、正しく計算されません。
面積の計算は、非常に簡単なのですが、入力ミスの判定にプログラムの大半を使っています。
簡単に判定できるアルゴリズムが見つけられると良いのですが。
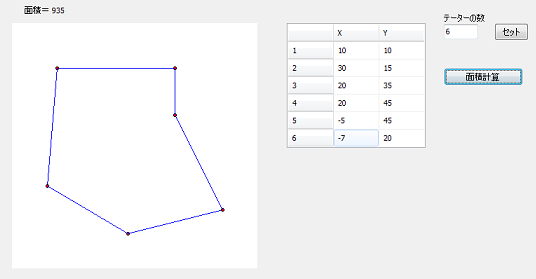
データーの数をセットし、セットボタンをクリックして、入力グリッドの設定をします。
次に、左回りにデーターを入力、全て入力が終わったら、面積計算ボタンをクリックする事で面積が計算されます。
サンプルプログラム
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.Grids, Vcl.StdCtrls, Vcl.ExtCtrls;
type
TForm1 = class(TForm)
DataNoEdit: TLabeledEdit;
DataNoSet: TButton;
StringGrid1: TStringGrid;
CalcBtn: TButton;
Image1: TImage;
procedure FormCreate(Sender: TObject);
procedure DataNoSetClick(Sender: TObject);
procedure CalcBtnClick(Sender: TObject);
procedure Area_Calc; // 面積計算
private
{ Private 宣言 }
procedure DataNumberset; // StringGrid1の設定
procedure Graph; // 図形表示
function Cross_Check(Xs1, Ys1, Xe1, Ye1, Xs2, Ys2, Xe2, Ye2: Double): Boolean; // 交差チェック
function Data_Check: Boolean; // 入力データー確認
function Cross3Check: Boolean; // 三点連結線と、直線の交差チェック
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses System.Math;
var
N : Integer; // データーの数
Xd : array of double; // X座標
Yd : array of double; // Y座標
S : Double; // 面積
Xmin : Double;
Xmax : Double;
Ymin : Double;
Ymax : Double;
Scale : Double;
GsMax : Double; // 交差判定時の誤差による語検知防止用
// 三点連結線と、直線の交差チェック
function TForm1.Cross3Check: Boolean;
label
che;
var
M : integer;
i, c, j, k, l : Integer;
o : Integer;
Q1, Q2, Q3 : Double;
Li, Lj : Double;
Yic, Yjc : Double;
CF, DF : Boolean;
a1, a2 : Double;
c1, c2 : Double;
xc, yc : Double;
XF, YF : Boolean;
begin
Result := True;
a1 := 0;
a2 := 0;
yc := 0;
xc := 0;
c1 := 0;
c2 := 0;
if N < 5 then exit;
M := N -1;
for i := 0 to M do begin
c := i + 1; // 第一の辺i,c
if c > M then c := c - M - 1;
j := c + 1; // 第一の辺c,j
if j > M then j := j - M - 1;
// i + 3 は3点連結線の次の点 M + i - 1 は 3点連結線の二つ前
for o := i + 3 to M + i - 1 do begin
CF := False; // 垂直判定フラグ初期化
DF := False;
k := o;
if k > M then k := k - M - 1; // 交差対象辺k,l
l := k + 1;
if l > M then l := l - M - 1;
if Xd[i] = Xd[c] then CF := true // 最初の辺X差分ゼロフラグ 垂直辺
else a1 := (Yd[i] - Yd[c]) / (Xd[i] - Xd[c]);
if Xd[k] = Xd[l] then DF := true // 対象辺X差分ゼロフラグ 垂直辺
else a2 := (Yd[k] - Yd[l]) / (Xd[k] - Xd[l]);
// 傾斜 a の値が計算できたら、定数項 C の値計算
if not CF then c1 := Yd[c] - a1 * Xd[c];
if not DF then c2 := Yd[l] - a2 * Xd[l];
// 垂直平行線の場合
if CF and DF then goto Che; // 交差しないので此処まで
// 二辺とも傾斜 a を計算したら
if not CF and not DF then begin
if a1 = a2 then goto Che; // 傾斜が等しい場合平行なので此処まで
xc := (c2 - c1) / (a1 - a2); // 交点Xの計算
yc := a1 * Xc + c1; // 交点Yの計算
end;
// 最初の辺垂直線の場合の 交点計算
if CF and not DF then begin
xc := Xd[i]; // 最初の辺垂直だったら 最初の辺Xの値
yc := a2 * xc + c2; // 交点Yの計算
end;
// 対象の辺垂直線の場合の 交点計算
if DF and not CF then begin
xc := Xd[k]; // 対象辺垂直だったら 対象辺Xの値
yc := a1 * xc + c1; // 交点Yの計算
end;
// 交点が最初の二辺の共通点と一致しなかったら此処まで 1e-10 は演算誤差見込み
if (abs(xc - Xd[c]) > 1e-10) or (abs(yc - Yd[c]) > 1e-10) then goto che;
XF := False; // 辺上の点かの判定フラグ初期化
YF := False;
// Xc と yc が 対象辺の 範囲内か確認
// X 方向確認
if Xd[l] = Xd[k] then XF := True
else begin
if Xd[l] > Xd[k] then begin
if (Xd[c] > Xd[k]) and (Xd[l] > Xd[c]) then XF := True;
end
else
if (Xd[c] < Xd[k]) and (Xd[l] < Xd[c]) then XF := True;
end;
// y 方向確認
if Yd[l] = Yd[k] then YF := True
else begin
if Yd[l] > Yd[k] then begin
if (Yd[c] > Yd[k]) and (Yd[l] > Yd[c]) then YF := True;
end
else
if (Yd[c] < Yd[k]) and (Yd[l] < Yd[c]) then YF := True;
end;
// 範囲内だったら座標変換 三点2辺の両端の点座標 対象辺の角度で水平方向へ座標変換
if XF and YF then begin
Q1 := arctan2(Yd[c] - Yd[i], Xd[c] - Xd[i]);
Q2 := arctan2(Yd[c] - Yd[j], Xd[c] - Xd[j]);
Q3 := arctan2(Yd[l] - Yd[k], Xd[l] - Xd[k]);
Li := sqrt((Yd[c] - Yd[i]) * (Yd[c] - Yd[i]) + (Xd[c] - Xd[i]) * (Xd[c] - Xd[i]));
Lj := sqrt((Yd[j] - Yd[c]) * (Yd[j] - Yd[c]) + (Xd[j] - Xd[c]) * (Xd[j] - Xd[c]));
Yic := sin(Q1 - Q3) * Li;
Yjc := sin(Q2 - Q3) * Lj;
if abs(Yic) < 1e-10 then Yic := 0; // 1e-10 は演算誤差見込み
if abs(Yjc) < 1e-10 then Yjc := 0; // 1e-10 は演算誤差見込み
// 三点2辺の両端の点座標 Y方向が プラスとマイナス方向にあったら交差あり
if ((Yic > 0) and (Yjc < 0)) or ((Yic < 0) and (Yjc > 0)) then Result := False;
end;
che:
end;
end;
// if not Result then Application.MessageBox('*交差している辺があります*。','注意', 0);
end;
// 座標点を結ぶ直線が交差していないか確認します
// 交差なし True 交差あり False
function TForm1.Cross_Check(Xs1, Ys1, Xe1, Ye1, Xs2, Ys2, Xe2, Ye2: Double): Boolean; // 交差チェック
var
a1, a2 : Double; // 傾斜角
c1, c2 : Double;
af1,af2 : Boolean;
Xa : Double; // 交差するXの値
Ya : Double; // 交差するYの値
f1, f2 : Boolean;
begin
Result := True; // 戻り値初期設定必要
af1 := False; // 辺1垂直辺フラグ False 初期設定必要
af2 := False; // 辺2垂直辺フラグ False 初期設定必要
f1 := true; // 辺1交点なしフラグ初期設定必要
f2 := true; // 辺2交点なしフラグ初期設定必要
a1 := 1000; // 辺1傾斜
a2 := 1000; // 辺2傾斜
Xa := 0; // 交点X座標
Ya := 0; // 交点Y座標
c1 := 0; // 辺1定数項
c2 := 0; // 辺2定数項
// 一次方程式 Y = aX + C の a の値計算 座標 Xs Xeの値が等しい場合 a の値が
// がないのでフラグをセットします。
if Xe1 = Xs1 then af1 := true // X1差分ゼロフラグ 垂直辺
else a1 := (Ye1 - Ys1) / (Xe1 - Xs1);
if Xe2 = Xs2 then af2 := true // X2差分ゼロフラグ 垂直辺
else a2 := (Ye2 - Ys2) / (Xe2 - Xs2);
// 垂直平行線の場合
if af1 and af2 then exit; // 交差しないので此処まで
// 二辺とも傾斜 a を計算したら
if not af1 and not af2 then
if a1 = a2 then exit; // 傾斜が等しい場合平行なので此処まで
// 傾斜 a の値が計算できたら、定数項 C の値計算
if not af1 then c1 := Ys1 - a1 * Xs1;
if not af2 then c2 := Ys2 - a2 * Xs2;
// 垂直線の場合の 交点 X の値
if af1 then Xa := Xs1; // 辺1垂直だったら X1の座標値 交点Xの値
if af2 then Xa := Xs2; // 辺2垂直だったら X2の座標値 交点Xの値
// 交点が辺の範囲内かチェック
// 交点があったら f を False にセット
// 両方とも垂直でも平行でも無い場合
if not af1 and not af2 then begin
Xa := (c2 - c1) / (a1 - a2); // 交点Xの値計算
// 辺1チェック
if Ys1 = Ye1 then begin
if (Ys2 = Ys1) or (Ye2 = Ys1) then exit;
end;
if Xs1 < Xe1 then begin
if (Xa > Xs1) and (Xa < Xe1) then f1 := False;
end
else
if (Xa < Xs1) and (Xa > Xe1) then f1 := False;
// 辺2チェック
if Ys2 = Ye2 then begin
if (Ys1 = Ys2) or (Ye1 = Ys2) then exit;
end;
if Xs2 < Xe2 then begin
if (Xa > Xs2) and (Xa < Xe2) then f2 := False;
end
else
if (Xa < Xs2) and (Xa > Xe2) then f2 := False;
// 交点があると判定されたら戻り値を False に設定
if not f1 and not f2 then Result := False;
exit;
end;
// 辺1が垂直の場合
if af1 then
if (Xs2 = Xa) or (Xe2 = Xa) then exit; // 辺2の両端点のXのどちらかがXaと同じだったら此処まで
// 辺2が垂直の場合
if af2 then
if (Xs1 = Xa) or (Xe1 = Xa) then exit; // 辺1の両端点のXのどちらかがXaと同じだったら此処まで
// 片方が垂直線の場合 Y の値確認
f1 := True;
f2 := True;
// X の値からY の値計算
if not af1 then Ya := a1 * Xa + c1;
if not af2 then Ya := a2 * Xa + c2;
// 辺1確認
if Ys1 < Ye1 then begin
if (Ya > Ys1) and (Ya < Ye1) then f1 := False;
end
else
if (Ya > Ye1) and (Ya < Ys1) then f1 := False;
// 辺2確認
if Ys2 < Ye2 then begin
if (Ya > Ys2) and (Ya < Ye2) then f2 := False;
end
else
if (Ya > Ye2) and (Ya < Ys2) then f2 := False;
// 交点があると判定されたら戻り値を False に設定
if not f1 and not f2 then Result := False;
end;
function TForm1.Data_Check: Boolean; // 入力データー確認
var
i, j, k : Integer;
begin
Result := true; // 戻り値初期設定
for i := 0 to N - 2 do // N - 1 が最後の点なのでその1つ前までループ
for k := i + 2 to N - 1 do begin // i + 2 から最後の点までループ (i + 1の点は二辺共通点なので交差なし)
if k < N - 1 then j := k + 1 // 最後の点でなかったら次の点は一つ先
else j := 0; // 最後の点だったら、次の点は最初の点
// 二辺の交差チェック True で交差なし
if i <> j then // i と j が等しいと二辺の共通点なので交差なし
Result := Cross_Check(Xd[i], Yd[i], Xd[i + 1], Yd[i + 1], Xd[k], Yd[k], Xd[j], Yd[j]);
if not Result then exit;
end;
end;
procedure TForm1.Graph; // 図形表示
var
j,m : Integer;
Xdiff : Double;
Ydiff : Double;
Xp,Yp : Integer;
begin
// 前の図形消去
Image1.Canvas.Brush.Style := bsSolid;
Image1.Canvas.Brush.Color := clWhite;
Image1.Canvas.FillRect(Rect(0, 0, Image1.Width, Image1.Height));
// 最小値最大値検索
Xmin := MinValue(Xd);
Xmax := MaxValue(Xd);
Ymin := MinValue(Yd);
Ymax := MaxValue(Yd);
// 範囲計算
Xdiff := Xmax - Xmin;
Ydiff := Ymax - Ymin;
// 表示スケール設定
if Xdiff > Ydiff then begin
GsMax := Xdiff;
Scale := 250 / Xdiff;
end
else begin
GsMax := Ydiff;
Scale := 250 / Ydiff;
end;
// 辺のと座標点の作図
for j := 0 to N do begin // j が Nになったら最初の座標点
if j = N then m := 0 // 一周後の配列の最初の値
else m := j; // 通常の座標
Xp := 50 + Round((Xd[m] - Xmin) * Scale); // Xの位置計算
Yp := 350 - Round((Yd[m] - Ymin) * Scale) - 50; // Yの位置計算
Image1.Canvas.Pen.Style := psSolid;
Image1.Canvas.Pen.Color := clBlue;
Image1.Canvas.Pen.Width := 1;
if j = 0 then Image1.Canvas.MoveTo(Xp, Yp) // 最初の点へ移動
else Image1.Canvas.LineTo(Xp, Yp); // 最初の点でなかったら線を引く
if j < N then begin // 最初の点に戻っていなかったら実行
Image1.Canvas.Pen.Color := clBlack;
Image1.Canvas.Brush.Color := clRed;
Image1.Canvas.Ellipse(Xp - 2, Yp - 2, Xp + 3, Yp + 3); // 円を描画中を塗りつぶし
end;
end;
end;
// 面積計算 1/2Σ(Xk - Xk+1)(Yk + Yk+1)
procedure TForm1.Area_Calc;
var
K : Integer;
J : Integer;
begin
S := 0;
for K := 0 to N -1 do begin
if K < N - 1 then J := K + 1 // 次の座標 j = k + 1
else J := 0; // 最後の座標になったら 次の座標は最初の座標 j = 0
S := S + (Xd[K] - Xd[J]) * (Yd[K] + Yd[J]); // Σ(Xk - Xj)(Yk + Yj)
end;
S := Abs(S / 2); // 1/2 にして絶対値
Form1.Canvas.TextOut(50, 15, '面積= ');
Form1.Canvas.TextOut(50, 15, '面積= ' + floatTostr(S));
Graph; // 図形表示
end;
procedure TForm1.CalcBtnClick(Sender: TObject); // 入力データー処理 と 面積計算 辺の交差確認
var
Check : Integer;
I : Integer;
Cmt : Pchar;
begin
for I := 0 to N - 1 do begin
Val(StringGrid1.Cells[1, I + 1], Xd[I], Check);
if Check <> 0 then begin
Cmt := PChar('Xデーター' + intTostr(I + 1) + '番目に間違いがあります');
Application.MessageBox(Cmt,'注意', 0);
Break;
exit;
end;
end;
for I := 0 to N - 1 do begin
Val(StringGrid1.Cells[2, I + 1], Yd[I], Check);
if Check <> 0 then begin
Cmt := PChar('Yデーター' + intTostr(I + 1) + '番目に間違いがあります');
Application.MessageBox(Cmt,'注意', 0);
Break;
exit;
end;
end;
Area_Calc; // 面積計算
if not Data_Check then // 辺の交差確認
Application.MessageBox('交差している辺があります。','注意', 0);
if not Cross3Check then
Application.MessageBox('*交差している辺があります*。','注意', 0);
end;
procedure TForm1.DataNumberset; // StringGrid1の設定 XY配列の確保
var
K : Integer;
begin
Val(DataNoEdit.Text, N, K); // データーの数 数値変換
if K <> 0 then begin
Application.MessageBox('データーの数に間違いがあります','注意', 0);
exit;
end;
if N < 3 then begin
Application.MessageBox('データーの数は3又は3以上にして下さい。','注意', 0);
exit;
end;
K := 3; // 列数 3
StringGrid1.Width := (StringGrid1.DefaultColWidth + 1) * K + 3;
if N < 11 then begin // データー数11以下の場合
StringGrid1.ScrollBars := ssNone;
K := N + 1; // 行数 N + 1
StringGrid1.Height := (StringGrid1.DefaultRowHeight + 1) * K + 3;
end else
begin
K := 11; // 行数 10 + 1
StringGrid1.ScrollBars := ssVertical;
StringGrid1.Width := StringGrid1.Width + 18;
StringGrid1.Height := (StringGrid1.DefaultRowHeight + 1) * K + 3;
end;
StringGrid1.RowCount := N + 1; // 行数セット
for K := 1 to N + 1 do // データー番号グリッドに表示
StringGrid1.Cells[0 , K] := InttoStr(K);
SetLength(Xd, N); // X座標配列の確保
SetLength(Yd, N); // y座標配列の確保
end;
procedure TForm1.DataNoSetClick(Sender: TObject);
begin
DataNumberset;
end;
procedure TForm1.FormCreate(Sender: TObject);
var
BitMapD : Tbitmap;
begin
ClientHeight := 410;
ClientWidth := 840;
StringGrid1.Cells[0 , 0] := '';
StringGrid1.Cells[1 , 0] := 'X';
StringGrid1.Cells[2 , 0] := 'Y';
// ************* テストデーター ************
DataNoEdit.Text := '5';
StringGrid1.Cells[1 , 1] := '0';
StringGrid1.Cells[2 , 1] := '0';
StringGrid1.Cells[1 , 2] := '20';
StringGrid1.Cells[2 , 2] := '0';
StringGrid1.Cells[1 , 3] := '10';
StringGrid1.Cells[2 , 3] := '10';
StringGrid1.Cells[1 , 4] := '20';
StringGrid1.Cells[2 , 4] := '20';
StringGrid1.Cells[1 , 5] := '0';
StringGrid1.Cells[2 , 5] := '20';
// *****************************************
DataNumberset;
Image1.Width := 350;
Image1.Height := 350;
BitMapD := Tbitmap.Create;
BitMapD.Width := Image1.Width;
BitMapD.Height := Image1.Height;
Image1.Picture.Graphic := BitMapD;
BitMapD.Free;
end;
end.
![]() Polygon_area.zip
Polygon_area.zip
各種プログラム計算例に戻る