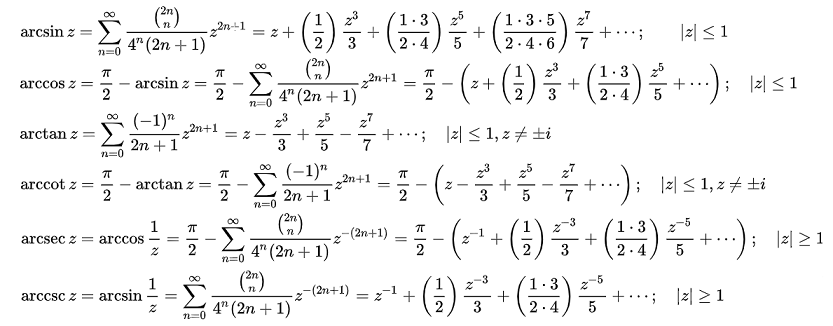
逆三角関数　無限級数計算

　逆三角関数の計算を無限級数を用いて計算します。

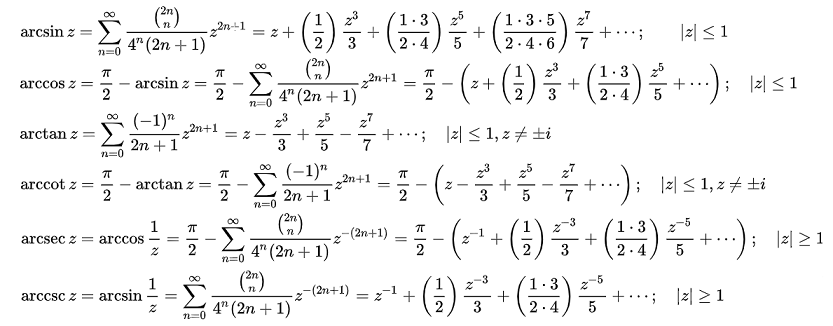
レオンハルト・オイラーの計算

詳細については　 ウィキペディア　逆三角関数　を参照してください。

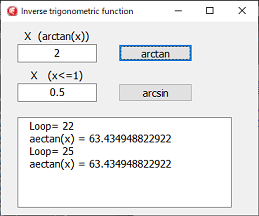　プログラムは、arcsinとarctanしか作成していませんが、arccosは π/2 -arcsin(x)で計算が出来るように、他の逆三角関数も計算が出来ます。
更に、 ピタゴラスの定理と、三角比の定義を利用すれば、どれか一つの逆三角関数が計算できれば、全て計算が可能となります。

　問題は、無限級数なので、arcsin(ｘ)の時、xの値が１に近づくと、計算のループ数が増え計算に時間がかかります。
そこで、45°X=0.7 辺りを境にして、π/2-arccos(X)を計算します。
arcsin(1)の時、π/2-arccos(0)となり無限にループ数が増えるのを防ぐことができ、Doubleの精度で多くても３０ループ以下で計算が収束します。
 ピタゴラスの定理と、三角比の定義を利用すればarccos(x) = arcsin(√(１-x²))で計算計算が出来ます。
arccos(ｘ)、arctan(x)や他の逆三角関数も同様な処理をして計算ループ数を少なくすることができます。
　通常の無限級数の場合arctan(x)の値が１に近づくと、ループ数が非常にふえます、45°の時が１なので通常の無限級数計算では、ループ数を減らす事はできません。
　arctan(ｘ)の計算に レオンハルト・オイラーの計算があり、ｘの値が１に近づく、或いは１になっても、ループ数は、左程増えません。また、１を超えても計算が可能ですが、ループ数が増加します、そこで１を超えたら、π/2－arctan(1/X)とすることで、他の計算と同じようにループ数を減らすことが出来ます。

プログラム

unit Main;

interface

uses
  Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
  Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.Buttons, Vcl.ExtCtrls;

type
  TForm1 = class(TForm)
    LabeledEdit1: TLabeledEdit;
    BitBtn1: TBitBtn;
    LabeledEdit2: TLabeledEdit;
    BitBtn2: TBitBtn;
    Memo1: TMemo;
    procedure BitBtn1Click(Sender: TObject);
    procedure BitBtn2Click(Sender: TObject);
  private
    { Private 宣言 }
  public
    { Public 宣言 }
  end;

var
  Form1: TForm1;

implementation

{$R *.dfm}

uses system.Math;

// arctan
// 1 を越えたら反対側の角度を計算
// レオンハルト・オイラーの計算
function arctan_routine(x: double): double;
var
  i : integer;
  ax, y, ans, bans, f: double;
begin
  ax := x;
  if x > 1 then ax := 1 / x;
  y := (ax * ax)/(1 + ax * ax);
  i := 1;
  ans := 1;
  f := 1;
  repeat
    bans := ans;
    f := f * i * 2 / (i * 2 + 1) * y;
    ans := ans  + f;
    inc(i);
  until (bans = ans) or (i > 10000);
  ans := ans  * y / ax;
  if x > 1 then ans := pi / 2 - ans;
  result := ans;
  form1.Memo1.Lines.Append('  Loop= ' + intTostr(i-1));
end;

// 1 を越えたら反対側の角度を計算
function arctanM_routine(x: double): double;
var
  i : integer;
  tx, ans, bans, f: double;
begin
  tx := x;
  if x > 1 then tx := 1 / x;
  ans := tx;
  f := tx;
  i := 1;
  repeat
    bans := ans;
    f := - f * tx * tx;
    ans := ans  + f / (i * 2 + 1);
    inc(i);
  until (bans = ans) or (i > 10000000);
  if x > 1 then ans := pi / 2 - ans;
  result := ans;
  form1.Memo1.Lines.Append('  Loop= ' + intTostr(i-1));
end;

// arcsin
// xの値が0.999999位が限度
function arcsin_routine(x: double): double;
label
  EXT;
var
  i : integer;
  ans, bans, f, d: double;
begin
  i := 1;
  if x = 1 then begin
    result := pi / 2;
    goto EXT;
  end;
  f := 1 / 2;
  d := x * x * x;
  ans := (x + f * d / 3);
  repeat
    bans := ans;
    d := d * x * x;
    f := f * (i * 2 + 1) / ((i + 1) * 2);
    ans := ans + f * d / (i * 2 + 3);
    inc(i);
  until (bans = ans) or (i > 10000000);
  result := ans;
EXT:
  form1.Memo1.Lines.Append('  Loop= ' + intTostr(i - 1));
end;

// 0.7を超えたら反対側の角度を求めます(cos計算になります)
function arcsinM_routine(x: double): double;
label
  EXT;
var
  i : integer;
  ax, ans, bans, f, d: double;
begin
  i := 1;
//  if x = 1 then begin
//    result := pi / 2;
//    goto EXT;
//  end;
  ax := x;
  if x > 0.7 then ax := sqrt(1 - x * x);
  f := 1 / 2;
  d := ax * ax * ax;
  ans := (ax + f * d / 3);
  repeat
    bans := ans;
    d := d * ax * ax;
    f := f * (i * 2 + 1) / ((i + 1) * 2);
    ans := ans + f * d / (i * 2 + 3);
    inc(i);
  until (bans = ans) or (i > 1000);
  if x > 0.7 then ans := pi / 2 - ans;
  result := ans;
EXT:
  form1.Memo1.Lines.Append('  Loop= ' + intTostr(i - 1));
end;

// arctan 計算
procedure TForm1.BitBtn1Click(Sender: TObject);
var
  ch : integer;
  x, ax, at, deg : double;
begin
  val(Labelededit1.Text, x, ch);
  if ch <> 0 then begin
    application.MessageBox('入力値に間違い化があります。','注意',0);
    exit;
  end;
  Memo1.Clear;
  ax := abs(x);
  at := arctan_routine(ax);
  if x < 0 then at := -at;
  deg := at / pi * 180;
  Memo1.Lines.Append('  aectan(x) = ' + floatTostr(deg));
  at := arctanM_routine(ax);
  if x < 0 then at := -at;
  deg := at / pi * 180;
  Memo1.Lines.Append('  aectan(x) = ' + floatTostr(deg));
end;

// arcsin 計算
procedure TForm1.BitBtn2Click(Sender: TObject);
var
  ch : integer;
  x, ax, asi, deg : double;
begin
  val(Labelededit2.Text, x, ch);
  if ch <> 0 then begin
    application.MessageBox('入力値に間違いがあります。','注意',0);
    exit;
  end;
  if abs(x) > 1 then begin
    application.MessageBox('入力値が大きすぎます。(X ≧ 1)','注意',0);
    exit;
  end;
  Memo1.Clear;
  ax := abs(x);
  asi := arcsin_routine(ax);
  if x < 0 then asi := -asi;
  deg := asi / pi * 180;
  Memo1.Lines.Append('  aecsin(x) = ' + floatTostr(deg));
  asi := arcsinM_routine(ax);
  if x < 0 then asi := -asi;
  deg := asi / pi * 180;
  Memo1.Lines.Append('  aecsin(x) = ' + floatTostr(deg));
end;

end.

　InverseA_trigonometric_function.zip

　　三角関数、逆三角関数、その他関数　に戻る