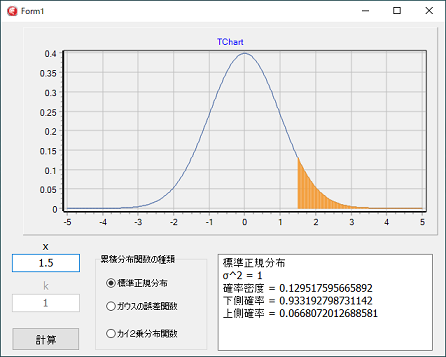
不完全ガンマ関数の応用

　標準正規分布、ガウスの誤差関数、カイ２乗分布の計算です。

詳細については、標準正規分布は、ウィキペディア　正規分布を、 ガウスの誤差関数はウィキペディア　ガウスの誤差関数を、カイ２乗分布は、ウィキペディア カイ２乗分布を、それぞれ参照してください。

プログラムは、Ｃ言語辞典　アルゴリズムにある不完全ガンマ関数のC言語プログラムをDelphi用に変換してグラフを追加したものです。
C言語辞典では、不完全ガンマ関数となっていますが、本来の不完全ガンマ関数とは値が一致しませんので注意が必要です、あくまでも応用です。

プログラム

unit Main;

interface

uses
  Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
  Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, VclTee.TeeGDIPlus,
  VCLTee.Series, VCLTee.TeEngine, Vcl.ExtCtrls, VCLTee.TeeProcs, VCLTee.Chart,
  Vcl.Buttons, system.UITypes;

type
  TForm1 = class(TForm)
    Memo1: TMemo;
    LabeledEdit1: TLabeledEdit;
    BitBtn1: TBitBtn;
    LabeledEdit2: TLabeledEdit;
    Chart1: TChart;
    Series1: TLineSeries;
    Series2: TLineSeries;
    Series3: TPointSeries;
    Series4: TPointSeries;
    GroupBox1: TGroupBox;
    RadioButton1: TRadioButton;
    RadioButton2: TRadioButton;
    RadioButton3: TRadioButton;
    procedure BitBtn1Click(Sender: TObject);
    procedure RadioButton3Click(Sender: TObject);
    procedure RadioButton2Click(Sender: TObject);
    procedure RadioButton1Click(Sender: TObject);
  private
    { Private 宣言 }
  public
    { Public 宣言 }
  end;

var
  Form1: TForm1;

implementation

{$R *.dfm}

const

//ベルヌーイ数B(2)、B(4)、B(6)、...、B(16)

  B : array[1..8] of double = ( 1.0 / 6,           // B(2)
                                  -1.0 / 30,
                                   1.0 / 42,
                                  -1.0 / 30,
                                   5.0 / 66,
                                -691.0 / 2730,
                                   7.0 / 6,
                               -3617.0 / 510);         // B(16)

  m: integer = sizeof(B) div sizeof(double);

function logGamma(x: double): double;  // ガンマ関数の対数
var
  i : integer;
  sum : double;
  xx, v  : double;
  xj  : double;
  lng : double;
  ln_sqrt_2pi: double;
begin
  ln_sqrt_2pi := ln(sqrt(2 * pi));                    // = ln(2 * pi) / 2;
  sum := 0;
  v := 1;
  while x < m do begin
    v := v * x;
    x := x + 1;
  end;
  xx := x * x;
  xj := x;
  lng := ln_sqrt_2pi - x + (x - 0.5) * ln(x) - ln(v);
  for i := 1 to  m do begin
    sum := sum + B[i] / (i * 2 * (2 * i - 1)) / xj;
    xj := xj * xx;
  end;
  result := sum + lng;
end;

function q_gamma(a, x, loggamma_a: double): double; forward;

// γ(a, x, lnΓ(a))
function p_gamma(a, x, loggamma_a: double): double;
var
  k : integer;
  term, previous : double;
begin
  result := 0;
  if x = 0 then exit;
  if x >= 1 + a then begin
    result :=  1 - q_gamma(a, x, loggamma_a);
    exit;
  end;
  term := exp(a * ln(x) - x - loggamma_a) / a;
  result := term;
  for k := 1 to 1000 do begin
    term := term * x / (a + k);
    previous := result;
    result := result + term;
    if result = previous then begin
      exit;
    end;
  end;
  Form1.Memo1.Lines.add ('p_gamma: 収束しません');
end;

// Γ(a, x, lnΓ(a))
function q_gamma(a, x, loggamma_a: double): double;
var
  k : integer;
  w, temp, previous : double;
  la, lb : double;
begin                 // Laguerreの多項式
  la := 1;
  lb := 1 + x - a;
  if x < 1 + a then begin
    result := 1 - p_gamma(a, x, loggamma_a);
    exit;
  end;
  w := exp(a * ln(x) - x - loggamma_a);
  result := w / lb;
  for k := 2  to 1000 do begin
    temp := ((k - 1 - a) * (lb - la) + (k + x) * lb) / k;
    la := lb;
    lb := temp;
    w := w * (k - 1 - a) / k;
    temp := w / (la * lb);
    previous := result;
    result := result + temp;
    if result = previous then exit;
  end;
  Form1.Memo1.Lines.add ('q_gamma: 収束しません');
end;

function p_chisq(chisq: double; df: integer): double;   // カイ2乗分布の下側確率
begin
  esult := p_gamma(0.5 * df, 0.5 * chisq, loggamma(0.5 * df));
end;

function q_chisq(chisq: double; df: integer): double;   // カイ2乗分布の上側確率
begin
  result := q_gamma(0.5 * df, 0.5 * chisq, loggamma(0.5 * df));
end;

const
  LOG_PI = 1.14472988584940017;

function erf(x: double): double;      // Gaussの誤差関数
begin
  if x >= 0 then result := p_gamma(0.5, x * x, LOG_PI / 2)
	   else result :=  - p_gamma(0.5, x * x, LOG_PI / 2);
end;

function erfc(x: double): double;     // 1 - erf(x)
begin
  if x >= 0 then  result := q_gamma(0.5, x * x, LOG_PI / 2)
	   else  result := 1 + p_gamma(0.5, x * x, LOG_PI / 2);
end;

function p_normal(x: double): double; // 標準正規分布の下側確率
begin
  if x >= 0 then result := 0.5 * (1 + p_gamma(0.5, 0.5 * x * x, LOG_PI / 2))
	   else result := 0.5 * q_gamma(0.5, 0.5 * x * x, LOG_PI / 2);
end;

function q_normal(x: double): double; // 標準正規分布の上側確率
begin
  if x >= 0 then result := 0.5 * q_gamma(0.5, 0.5 * x * x, LOG_PI / 2)
	   else result := 0.5 * (1 + p_gamma(0.5, 0.5 * x * x, LOG_PI / 2));
end;


procedure TForm1.BitBtn1Click(Sender: TObject);
var
  ch : integer;
  x, xi, y : double;
  k : integer;
  UP, DW  : double;
  MIN, MAX: double;
  dx     : double;
  i : integer;

  // 標準正規分布確率密度 σ^2 = 1
  function normal(x: double): double;
  begin
    result := exp(- (x * x) / 2) / sqrt(2 * pi);
  end;

begin
  Memo1.Clear;
  val(LabeledEdit1.Text, x, Ch);
  if ch <> 0 then begin
    MessageDlg('xの値に間違いがあります。', mtInformation,
      [mbOk], 0, mbOk);
    exit;
  end;
  if radiobutton3.Checked then
    if x < 0 then begin
      MessageDlg('負数のxは計算出来ません', mtInformation,
       [mbOk], 0, mbOk);
      exit;
    end;
  val(LabeledEdit2.Text, k, Ch);
  if ch <> 0 then begin
    MessageDlg('kの値に間違いがあります。', mtInformation,
      [mbOk], 0, mbOk);
    exit;
  end;
  if k <= 0 then begin
    MessageDlg('kはゼロより大きくして下さい計算出来ません。', mtInformation,
      [mbOk], 0, mbOk);
    exit;
  end;
//  UP := 0;
  DW := 0;
  if radiobutton1.Checked then begin
    UP := q_normal(x);
    DW := p_normal(x);
    Memo1.Lines.Add('標準正規分布');
    Memo1.Lines.Add('σ^2 = 1');
    y := normal(x);
    Memo1.Lines.Add('確率密度 = ' + floattostr(y));
    Memo1.Lines.Add('下側確率 = ' + floatTostr(DW));
    Memo1.Lines.Add('上側確率 = ' + floatTostr(UP));
  end;
  if radiobutton2.Checked then begin
    DW := erf(x);
    UP := erfc(x);
    Memo1.Lines.Add('ガウスの誤差関数');
    Memo1.Lines.Add('erf  = ' + floatTostr(DW));
    Memo1.Lines.Add('erfc = ' + floatTostr(UP));
  end;
  if radiobutton3.Checked then begin
    y := 1 / (power(2, k / 2) * exp(loggamma(k / 2)));
    UP := power(x, k / 2 - 1);
    DW := exp(-x / 2);
    y := y * UP * DW;
    UP := q_chisq(x, k);
    DW := p_chisq(x, k);
    Memo1.Lines.Add('カイ２乗分布');
    Memo1.Lines.Add('確率密度 = ' + floattostr(y));
//    Memo1.Lines.Add('累積分布関数　F(' + floatTostr(x) + ';' + intTostr(k) + ')');
    Memo1.Lines.Add('下側確率 = ' + floatTostr(DW));
    Memo1.Lines.Add('上側確率 = ' + floatTostr(UP));
  end;
  Series1.Clear;
  Series2.Clear;
  Series3.Clear;
  Series4.Clear;
  if radiobutton1.Checked then begin
    Min := -5;
    MAX := 5;
    if x > MAX then MAX := x + 1;
    if x < MIN then MIN := x - 1;
    dx := (MAX - MIN) / 400;
    for i := 0 to 400 do begin
      xi := i * dx + MIN;
      y := normal(xi);
      Series1.AddXY(xi, y);
      if x <= xi then begin
        Series2.AddXY(xi, y);
        Series2.AddXY(xi, 0);
        Series2.AddXY(xi, y);
      end;
    end;
  end;
  if radiobutton2.Checked then begin
    Series3.AddXY(x, DW);
    Min := -3;
    MAX := 3;
    if x > MAX then MAX := x + 1;
    if x < MIN then MIN := x - 1;
    dx := (MAX - MIN) / 400;
    for i := 0 to 400 do begin
      xi := i * dx + MIN;
      y := erf(xi);
      Series1.AddXY(xi, y);
    end;
  end;
  if radiobutton3.Checked then begin
    Series4.AddXY(x, DW);
    Min := 0;
    MAX := 3;
    if x > MAX - 1 then MAX := x + 1;
    dx := (MAX - MIN) / 400;
    for i := 0 to 400 do begin
      xi := i * dx + MIN;
      y := p_chisq(xi, k);
      Series2.AddXY(xi, y);
    end;
  end;
end;

procedure TForm1.RadioButton1Click(Sender: TObject);
begin
  LabeledEdit2.Enabled := False;
end;

procedure TForm1.RadioButton2Click(Sender: TObject);
begin
  LabeledEdit2.Enabled := False;
end;

procedure TForm1.RadioButton3Click(Sender: TObject);
begin
  LabeledEdit2.Enabled := True;
end;

end.

　
　　　deviation_function.zip

各種プログラム計算例に戻る